基于改进人工蜂群算法的配电网重构

邓海潮，毛 弋，彭文强，刘小丽，梁 杉，范 幸（湖南大学电气与信息工程学院，长沙 410082）

基于改进人工蜂群算法的配电网重构

邓海潮，毛 弋，彭文强，刘小丽，梁 杉，范 幸
（湖南大学电气与信息工程学院，长沙 410082）

摘要：为了更好地解决配电网重构问题，采用改进人工蜂群算法，建立了以系统有功损耗为目标的重构模型。在该改进算法中，利用差分进化操作的思想对人工蜂群算法中的邻域搜索方式进行了改进，直接在离散域进行多维搜索代替原来的单维更新策略，提高了算法的探索能力并且加快了收敛速度。此外，为了克服基于比例适应度选择的不足，用基于适应度排序的选择概率替代基于比例适应度的选择概率，使得种群的多样性得到了保护，从而避免了陷入局部最优。该算法应用于配电网重构能够以较快的速度收敛到最优解，文中的算例结果验证了该算法用于网络重构是可行而且有效的。

关键词：人工蜂群算法；配电网重构；邻域搜索；适应度排序选择

配电网重构是配电网优化分析的重要内容，它是在满足系统约束的前提下通过改变段开关和联络开关的开闭状态来改变网络的拓扑结构，实现网络运行参数的优化，从而有效地降低网损，并能达到均衡负荷、提高供电质量等目的［1］。

配电网重构问题属于非线性组合优化问题。直至今日，求解配电网重构的主要算法也在不断改进，传统数学优化算法［2］可以得到全局最优解，但随着网络规模的增大，计算时间长并且易导致维数灾问题。最优流模式法［3］和支路交换法［4］在计算速度上有很大的提高，但易收敛于局部最优解。近年来应用较多的人工智能算法有遗传算法［5-6］、免疫算法［7］、粒子群算法［8］等，它们在获取全局最优解方面取得了较好的效果，但为了得到更广泛的应用必须减小重构时间并且提高搜索效率，另外多种智能算法结合［9-11］用于重构问题也越来越普遍，但也相应提高了算法的复杂度。

人工蜂群ABC（artificial bee colony）算法是Karaboga［12］于2005年提出的一种新的群集智能算法。它具有操作简单，控制参数少，鲁棒性强等优点，因而受到了广泛的关注，文献［13］已将其应用于配电网重构。但蜂群算法也存在局部搜索能力弱，收敛速度慢等缺点。基于此，本文对算法的邻域搜索方式进行了改进，采用多维搜索的方式替代单维更新策略，能够更广泛地搜索解空间，提高了算法开采效率且加快了收敛速度。另外，由于直接依据比例适应度的选择不利于算法的全局搜索，本文采用了适应度排序的选择概率，跳出了局部最优，保护了种群的多样性，引入自适应的机制平衡了全局与局部的搜索性能。将改进后的人工蜂群IABC （improved artificial bee colony）算法成功应用于配电网重构，并取得了良好的效果。

1 配电网重构的数学模型

配电网重构的目标有多种，常见的以网损最小为目标进行优化。本文选择以配电网网损最小为目标进行重构，其目标函数为

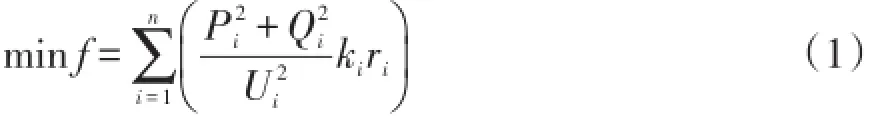
式中：i为支路编号；n为支路总数；ki为开关状态，0代表打开，1代表闭合；ri为支路i的电阻值；Pi、Qi分别表示支路i的有功功率及无功功率；Ui为支路末端的节点电压；f为系统网损。

配电网重构还需满足以下约束条件。

（1）潮流等式约束，系统各支路与节点需满足潮流方程。

（2）支路容量约束，即

式中：Si为流过支路i的功率；Si max为支路i允许流过的最大功率值。

（3）节点电压约束，即

式中，Ui max、Ui min分别为节点i允许的电压上、下限。

（4）网络拓扑约束，即配电网必须为辐射状并且无孤岛。

2 算法的基本原理

2.1 ABC算法

ABC算法是基于蜜蜂采蜜行为启发而提出的一种新型群集智能优化算法，其通过雇佣蜂、观察蜂、侦察蜂3种不同的角色在空间完成搜索的过程。初始化时，种群由雇佣蜂和观察蜂组成，且雇佣蜂的个数等于观察蜂的个数。在该算法中，食物源的位置代表优化问题的可行解，食物源的浓度代表可行解的质量（适应度值），而蜂群寻找食物源的过程就是求解最优问题的过程。

ABC算法的具体寻优过程如下：首先，由ABC算法产生SN个初始解（食物源），设第i个食物源的位置为Xi=（xi1，xi2，…，xiD）（i=1，2，…，SN），其中D为优化问题的维数，食物源与雇佣蜂一一对映。随机生成初始可行解的公式为

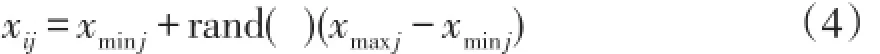
式中：xij表示食物源位置；xmax j和xmin j分别为第j维分量的上限和下限，j∈｛1，2，…，D｝；rand（ ）为（0，1）间的随机数，下同。

随后，蜂群对全部食物源开展循环搜索。雇佣蜂先在食物源附近进行一次邻域搜索，计算并且对比原来的食物源和搜索到的新食物源的适应度值，再在二者之间进行贪婪选择，若搜索到的新食物源优于原来的食物源，则用新的食物源取代原来的食物源，反之，仍保持原来的食物源信息不变。当所有的雇佣蜂完成搜索后，它们回到舞蹈区通过摇摆舞的形式将食物源的信息分享给观察蜂，观察蜂依据适应度值的大小以轮盘赌的方式按照一定的概率选择食物源，适应度值越优的食物源被选择的概率也就相应越大，并在已选择的食物源附近以同雇佣蜂一样的方式进行邻域搜索，在新旧食物源之间进行贪婪选择，选择其中较优的食物源。

在探索一个新的食物源位置时，雇佣蜂和观察蜂生成新的食物源Vi（Vi=（vi1，vi2，…，viD））的邻域搜索公式为

式中：vij表示新生成的食物源位置；k∈｛1，2，…，SN｝中的随机整数，且k≠i；jrand为［1，D］之间的某一维；rij为［-1，1］之间的随机数。

观察蜂对食物源进行选择的概率为

式中，fiti为第i个食物源的适应度值，适应度值与优化问题目标函数值对应关系为

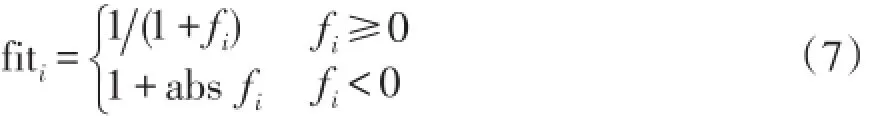
式中，fi为第i个食物源对应的目标函数值。

ABC算法就是通过以上的搜索方式进行不断的循环来完成寻优过程的，在该过程中，若某个食物源经过limit次循环后仍然没有更新，表示该解陷入局部最优，与之相对应的雇佣蜂放弃该食物源，并转换成一侦察蜂，按照式（4）在搜索空间探寻新的食物源位置替代原来的食物源位置。

为了解决离散优化问题，特别是针对组合优化问题，Marinakis等［14］于2009年在连续ABC算法的基础上提出了一种二进制编码的人工蜂群BABC（bi⁃nary artificial bee colony）算法。该算法通过sig函数将xij，vij由实数转换成二进制的0，1，以xij为例，转换方法为

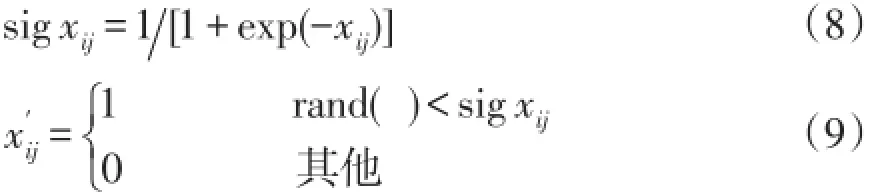
vij按照相同的方法进行变换，BABC算法的其他流程基本与ABC算法流程一致，在此不再赘述。

2.2 IABC算法

人工蜂群由雇佣蜂、观察蜂、侦察蜂3种不同的角色组成，其中雇佣蜂和观察蜂通过邻域搜索对食物源进行局部开采，而侦察蜂随机在空间搜寻新的食物源开展全局探索，因而该算法较好地平衡了全局探索与局部开采。但是，算法中的邻域搜索只是对食物源某一维进行更新，严重滞后了算法进化速度，同时，由于比例适应度选择策略的缺点，可能会错过潜在的较优个体，不利于种群的多样性。基于此，本文从这两方面对该算法进行改进。

2.2.1 多维邻域搜索策略

从ABC算法的邻域搜索式（5）可以看出，雇佣蜂和观察蜂在对原来食物源邻域进行搜索时，只是对其中的某一维进行更新，很容易造成新旧食物源相同，这在求解高维、离散问题时尤为突出，使得算法的进化速度慢，严重影响了算法的性能。

差分进化DE（differential evolution）算法［15］是一种根据个体间的差异信息来指导搜索的智能算法，在搜索速度方面有很强的优势。DE算法的交叉操作通过控制交叉概率的大小能够同时进行多个维度的变异，能搜索到更广泛的空间。受此思想的启发，本文将DE算法中的交叉操作引入邻域搜索公式，克服了原来只能进行单维更新的缺点，特别地，针对组合优化问题，为避免每次都要由连续域到离散域的变换，直接对连续域内邻域搜索式（5）进行离散化操作，改进后的离散域邻域搜索公式为

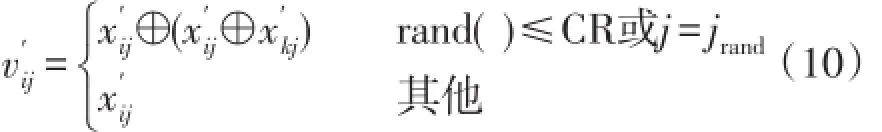
式中：CR为交叉概率；jrand为［1，D］之间的某一维，确保至少有一维发生交叉操作；⊕表示异或操作。在二元离散空间中，通常用海明距离描述个体间的差异，针对食物源位置的每一维变量，若某两维二进制位相同时，海明距离取1，否则取0，因而式（5）中xij-xkj用x⊕x来代替，rij在连续域中用来控制邻域产生范围，而在离散域中，1的邻域为0，0的邻域为1，故此处可将其省去。由式（5）可知，当xij与xkj相同时，对应v⊕x取0，vij值大小保持xij不变，对应=x；当xij与xkj不同时，对应x⊕x取1，vij值大小不等于xij，对应v=1-x，故在离散域中，可以通过x与x⊕x的异或操作实现上述运算。

式（10）实现了直接在离散域内通过多维更新的形式搜寻新的食物源，因而具有很强的搜索和开发能力，加快了收敛速度，提高了求解过程的效率。

2.2.2 基于排序的选择策略

在ABC算法中，观察蜂以一定概率对食物源的选择扮演了全局搜索的角色，其直接依赖于适应度的大小进行选择，使得适应度越高的食物源被选择的概率越大，而适应度较差的个体很可能被错过，但较劣的食物源也可能包含一些有用的信息，特别是在进化初期。另外，在进化后期，由于个体差异性小，很容易造成寻索过程停滞不前，陷入局部最优，不利于种群多样性。为了具有更好的全局收敛能力以及更强的鲁棒性，本文采用基于适应度排序的选择概率［16］，这种选择概率根据食物源的适应度大小进行排序，食物源被选择的概率仅仅决定于其次序，其中，第k个食物源被选择的概率为

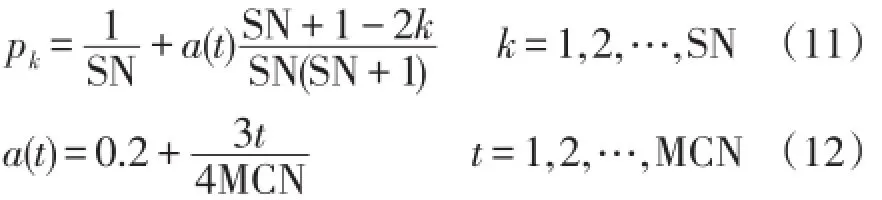
式中：a（t）为自适应参数；MCN为最大循环迭代次数。引入自适应参数机制，在算法的进化初期，a（t）较小，有利于搜寻到更多潜在可能最优的位置，而在进化后期，种群个体差异较小，竞争力减弱，可能造成算法停滞不前，较大a（t）可以提高搜索效率避免算法陷入局部最优而停滞。

3 基于IABC算法重构的实现步骤

将IABC算法应用于配电网重构，食物源的每一个位置代表不同的配电网络拓扑，食物源的适应度值反映了重构目标的优劣，蜂群寻找食物源的过程就是求解配电网重构的过程，算法的具体实现步骤如下：

（1）输入配电网初始信息并初始化，生成SN个原始食物源，设定交叉概率CR，雇佣蜂转换成侦察蜂对应的limit值，最大迭代次数MCN等；

（2）雇佣蜂在食物源附近按照式（10）对离散域进行邻域搜索产生新的食物源，并在新旧食物源v与x之间进行贪婪选择；

（3）观察蜂根据选择概率式（11）和式（12）对食物源进行选择，并在选择的食物源邻域按式（10）对离散域进行邻域搜索并进行贪婪选择；

（4）根据limit值判断是否有被放弃的解，若存在，则该处的雇佣蜂并转换成侦察蜂，在空间重新探寻新的食物源；

（5）记录目前最优解，判断是否达到最大迭代次数MCN，若达到，则停止计算，输出最优结果，否则返回步骤（2）继续循环。

4 算例分析

本文算例采用标准IEEE 33节点配电网系统［1］，如图1所示，该系统是一个额定电压为12.66 kV的配电网络，其中含有37条支路，33个节点，5个联络开关，系统总有功功率为3 715 kW，无功功率为2 300 kvar，该系统网络参数见文献［1］。在该算例中，设置参数SN为30，最大迭代次数MCN为50次，交叉概率CR为0.5，limit值为6，运行算法程序。

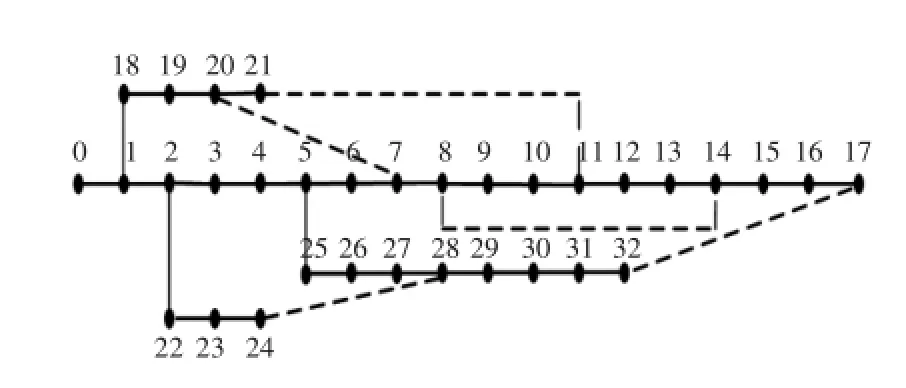
图1 IEEE 33节点配电网系统Fig.1 IEEE 33 nodes distribution network system

该节点配电网系统重构前打开的开关集为7-20、8-14、11-21、17-32、24-28，系统有功损耗为202.68 kW，节点最低电压为0.913 1 p.u.，重构后的结果及与相关方法所得结果对比如表1所示。

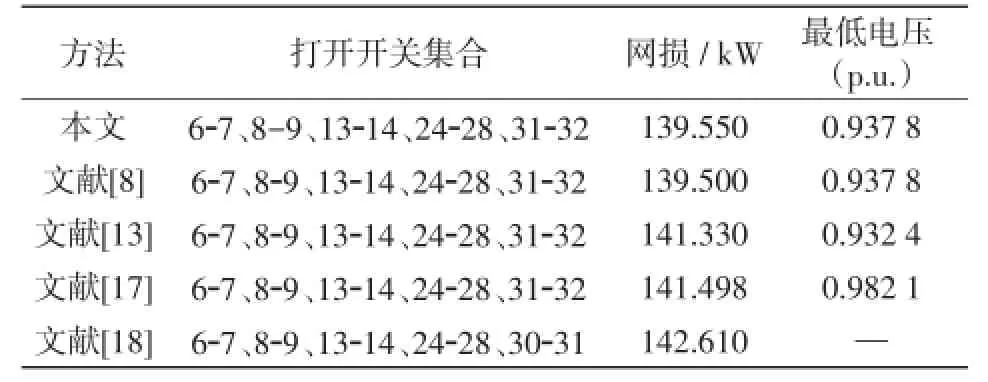
表1 重构后结果对比Tab.1 Result comparison after reconfiguration

由表1可知，采用IABC进行重构后断开的开关支路与文献［8，13，17］重构后结果一致，均为6-7、8-9、13-14、24-28、31-32，能够有效地获取全局最优解，而在文献［18］不含分布式电源的情形中，采用ABC算法进行重构后打开的开关集合为6-7、8-9、13-14、24-28、30-31，可以看出单纯地采用ABC算法进行配电网重构会陷入局部最优，造成全局收敛性能下降。应用本文方法后，网络有功损耗由重构前的202.68 kW下降为重构后的139.55 kW，降低了31.15%，网损较文献［13，17-18］有所降低，与文献［8］网损基本一致，由此可见本文算法的正确性和有效性，其中网损的细微区别是由潮流计算所用的方法的不同而出现偏差。此外，重构后网络节点最低电压由0.913 1 p.u.上升到0.937 8 p.u.，大多数节点电压有所提高，图2给出了重构前后系统节点电压比较。

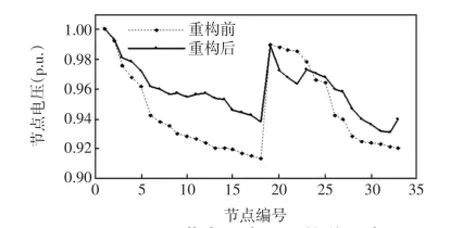
图2 IEEE 33节点配电系重构前后电压Fig.2 IEEE 33 node distribution network system voltages before and after reconfiguration

经多次运行，本文算法达到最优解时的平均迭代次数为16次左右，因此该算法具有较快的收敛速度，而在文献［8］中当收敛判据Ks，max取2时，平均迭代次数为16.6次，且Ks，max值越大，平均迭代次数越多，计算所耗时间也越多，文献［10］需要迭代68次，文献［17］在种群规模为50时平均迭代次数为18.37。虽然算法、初始化参数以及运行环境不尽相同，但从一定程度上反映了本文算法具有良好的收敛性能及鲁棒性。

5 结语

本文以降低网损为重构目标，在BABC算法的基础上，将差分进化操作的思想引入邻域搜索公式中，蜂群可以直接在离散域内进行多维搜索来更新位置，大大加快了算法的收敛速度。同时为了避免陷入局部最优，采用了基于适应度排序的选择策略，自适应机制有效地保护了种群的多样性，因而具有良好的全局收敛能力及鲁棒性。文中算例结果表明，该方法用于配电网重构能够以良好的全局性能和较快的收敛速度实现重构目标。

参考文献：

［1］Baran M E，Wu F F.Network reconfiguration in distribu⁃tion systems for loss reduction and load balancing［J］.IEEE Trans on Power Delivery，1989，4（2）：1401-1407．

［2］刘柏私，谢开贵，周家启（Liu Bosi，Xie Kaigui，Zhou Ji⁃aqi）.配电网重构的动态规划算法（Electrical distribu⁃tion networks reconfiguration using dynamic program⁃ming）［J］.中国电机工程学报（Proceedings of the CSEE），2005，25（9）：29-34．

［3］吴本悦，赵登福，刘云，等（Wu Benyue，Zhao Dengfu，Liu Yun，et al）.一种新的配电网络重构最优流模式算法（An improved optimal flow pattern algorithm for distribu⁃tion network reconfiguration）［J］.西安交通大学学报（Journal of Xi′an Jiaotong University），1999，33（4）：21-24．

［4］Civanlar S，Grainger J J，Yin H，et al.Distribution feed⁃er reconfiguration for loss reduction［J］.IEEE Trans on Power Delivery，1988，3（3）：1127-1223．

［5］胡雯，孙云莲，张巍（Hu Wen，Sun Yunlian，Zhang Wei）.基于改进的自适应遗传算法的智能配电网重构研究（Reconfiguration of smart distribution using improved adaptive genetic algorithm）［J］.电力系统保护与控制（Power System Protection and Control），2013，41（23）：85-90.

［6］张利民，马强，李振坤，等（Zhang Limin，Ma Qiang，Li Zhenkun，et al）.基于禁忌克隆遗传算法的配电网故障恢复重构（Service restoration reconfiguration in distribu⁃tion network based on tabu clonal genetic algorithm）［J］.电力系统及其自动化学报（Proceedings of the CSU-EP⁃SA），2010，22（1）：60-64.

［7］蒙文川，邱家驹（Meng Wenchuan，Qiu Jiaju）.基于免疫算法的配电网重构（An artificial immune algorithm to distribution network reconfiguration）［J］.中国电机工程学报（Proceedings of the CSEE），2006，26（17）：25-29．

［8］陈曦，程浩忠，戴岭，等（Chen Xi，Cheng Haozhong，Dai Ling，et al）.邻域退火粒子群算法在配电网重构中的应用（Application of simulated annealing particle swarm op⁃timization algorithm in reconfiguration of distribution net⁃works）［J］.高电压技术（High Voltage Engineering），2008，34（1）：148-153．

［9］尹洪，刘天琪，李樊，等（Yin Hong，Liu Tianqi，Li Fan，et al）.基于免疫遗传算法的含分布式电源配电网重构（Distribution network reconfiguration with different dis⁃tributed generation based on immune genetic algorithm）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2014，26（4）：15-19.

［10］罗绮，吕林（Luo Qi，Lü Lin）.一种新的混合优化算法求解配电网重构（A new hybrid optimal algorithm to solve distribution network reconfiguration）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2009，21（1）：89-92．

［11］刘畅，黄民翔（Liu Chang，Huang Minxiang）.含多种分布式电源的配电网重构优化研究（Distribution network re⁃configuration with a variety of DGs）［J］.电力系统保护与控制（Power System Protection and Control），2013，41 （6）：13-18.

［12］Karaboga D.An idea based on honey bee swarm for numer⁃ical optimization［R］.Kayseri：Engineering Faculty Com⁃puter Engineering Department of Erciyes University，2005.

［13］许贤杰，周玲，蒋丹，等（Xiu Xianjie，Zhou Ling，Jiang Dan，et al）.基于人工蜂群算法计及线路故障的配电网网络重构（Distribution network reconfiguration based on artificial bee colony algorithm and line fault）［J］.电测与仪表（Electrical Measurement&Instrumentation），2014，51（3）：33-36．

［14］Marinakis Y，Marinaki M，Matsatsinis N.A hybrid dis⁃crete artificial bee colony-GRASP algorithm for clustering ［C］//International Conference on Computers&Industrial Engineering.Troyes，France，2009：548-553．

［15］Engelbrecht A P，Pampara G.Binary differential evolution strategies［C］//IEEE Congress on Evolutionary Computa⁃tion.Singapore，2007：1942-1946.

［16］Bao Li，Zeng Jian-chao.Comparison and analysis of the se⁃lection mechanism in the artificial bee colony algorithm ［C］//9th International Conference on Hybrid Intelligent Systems.Shenyang，China，2009：411-416.

［17］孙涛，朱生鸿，李玥，等（Sun Tao，Zhu Shenghong，Li Yue，et al）.改进的分布估计算法在配网重构中的应用（Improved estimation of distribution algorithm in the ap⁃plication of distribution network reconfiguration）［J］.电力系统及其自动化学报（Proceedings of the CSU-EPSA），2014，26（6）：54-59.

［18］Muhtazaruddin M N，Jamian J J，Fujita G，et al.Distribu⁃tion network loss minimization via simultaneous distribut⁃ed generation coordination with network reconfiguration ［J］.Arab Journal for Science&Engineering，2014，39（6）：4923-4933．

邓海潮（1990—），男，硕士研究生，研究方向为电力系统优化运行。Email：emailsea@126.com

毛 弋（1965—），男，硕士，副教授，硕士生导师，研究方向为电力系统负荷预测、电力系统规划。Email：maoyidu@ya⁃hoo.com.cn

彭文强（1990—），男，硕士研究生，研究方向为配电网络优化运行。Email：pwqiang0904@sina.cn

中图分类号：TM72

文献标志码：A

文章编号：1003-8930（2016）07-0125-05

DOI：10.3969/j.issn.1003-8930.2016.07.023

作者简介：

收稿日期：2015-03-24；修回日期：2015-12-26

Distribution Network Reconfiguration Based on Improved Artificial Bee Colony Algorithm

DENG Haichao，MAO Yi，PENG Wenqiang，LIU Xiaoli，LIANG Shan，FAN Xing
（College of Electrical and Information Engineering，Hunan University，Changsha 410082，China）

Abstract：In order to deal with distribution network reconfiguration better，artificial bee colony algorithm was proposed to construct a mathematical model for distribution network reconfiguration in which the network loss minimization is built.In this improved algorithm，the search behaviors are modified by using the differential evolution operators.Origi⁃nal one-dimensional neighborhood search strategy is replaced by multidimensional neighborhood search strategy in the discrete domain，which improves the exploration ability and accelerates the converge speed of the algorithm.Moreover，to overcome the shortage of selection based on the proportion of fitness，the selection based on fitness ranking probabili⁃ty is adopted instead of depending on the proportion of fitness，which protects the diversity of the population and avoids premature convergence.The algorithm used in distribution network reconfiguration can converge at a faster rate to the optimal solution，and results of calculation examples show that the proposed algorithm is feasible and effective.

Key words：artificial bee colony algorithm；distribution network reconfiguration；neighborhood search；fitness ranking selection