基于改进粒子群算法的自动机性能评估

孙致远，郑　坚，熊　超，殷军辉

（军械工程学院，石家庄　050003）

基于改进粒子群算法的自动机性能评估

孙致远，郑坚，熊超，殷军辉

（军械工程学院，石家庄050003）

摘要：由于自行高炮自动机状态监测中缺乏行之有效的机构性能评估手段，引入了改进粒子群算法。建立了自动机动力学模型，对后坐过程进行了动力学仿真，确定了反映机构性能的浮动曲线特征量。针对粒子群算法收敛速度慢、精度低等缺陷，对其进行改进，并结合曲线特征量对自动机性能参数进行了评估。结果表明：改进后粒子群算法的算法收敛性和结果精度都有明显的改善，有效实现了自动机的性能参数评估。

关键词：改进粒子群算法，性能评估，动力学分析

0　引言

状态监测是装备故障预测与健康管理技术的前提和基础［1］，通过对装备进行有效的状态监测，可以准确获得装备机构的工况信息和性能状态，并判断其是否出现退化或故障，从而能够及时采取合理维修措施，提高装备可靠性。

在自行高炮的状态监测中，自行高炮连续射击时炮箱的浮动位移曲线能够全面反映自动机工作状态和内部机构性能。对其有效地分析处理，不仅可以得到高炮的射击频率、每管射弹数量和射击方式，而且还可以进一步对其内部导气装置、缓冲装置和浮动机等机构性能进行评估并判断是否出现退化等现象。

本文通过对某自行高炮自动机进行动力学分析，结合连续射击过程中浮动曲线的变化规律，确定了能够反映机构性能的浮动曲线特征量及其影响参数。针对粒子群算法（Particle Swarm Optimization，PSO）收敛速度慢、精度低等缺陷，对其进行改进，并结合浮动曲线特征量对自动机性能参数进行了全局寻优，有效实现了自动机性能评估，为准确掌握装备状态性能提供了一种可行的方法。

1　自动机运动特性分析

某自行高炮自动机为炮箱浮动近似定点定速式自动机，主要由身管部分、炮箱部分、炮闩部分、输弹机、浮动机和供弹机等机构组成。自行火炮连续射击时，炮闩部分在炮箱内部完成关闩击发及开锁后坐等动作，炮箱部分在悬置导轨上受膛内压力驱动，在浮动机约束下完成后坐复进，在炮闩撞击作用下完成二次后坐复进，实现自动机的浮动射击。建立自动机动力学仿真模型如图1所示。

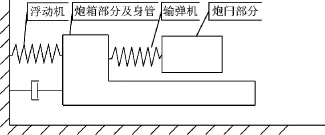
图1　自动机动力学模型

在自动机射击后坐阶段，炮闩闭锁与炮箱共同后坐，炮箱所受主动力、约束反力和阻力构成一个空间力系，分析各作用力，建立炮箱运动微分方程为：

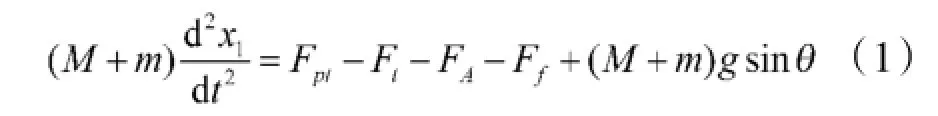
式中，M为自动机后坐部分质量，m为炮闩及输弹筒质量，x1为自动机后坐位移，Fpt为炮膛合力，根据膛压-时间数据求得；Ff为炮箱与导轨间摩擦力，θ为自动机高低射角；Ft为浮动机弹簧力，Ft=Ft0+K1· x1，Ft0为弹簧预压力，K1为弹簧刚度系数；FA为浮动机液压阻力［2］：

式中，K为液压阻力系数，ρ为缓冲液密度，A0为活塞工作面积，ax为流液孔面积。浮动机对于减小炮箱后坐冲击、提高自动机射击精度具有重要意义，通过改变浮动机内部各机构参数，能够控制炮箱各阶段运动位移及速度，易发生变化的参数主要为弹簧预压力Ft0，是调节浮动曲线的重要参数。

当炮闩开锁之后，输弹活塞受火药气体作用推动炮闩在炮箱滑道上移动。F=Ps·Ssh，Ps为气室内变化气压，Ssh为输弹活塞面积。由于火药气体作用输弹活塞运动距离只有不到50 mm，作用时间短，作用力大，炮闩和输弹筒可以简化为受到一个冲击，获得一个速度突变后向后运动。炮闩后坐初速度Vc的变化对自动机射弹周期、击发点位置及炮闩后坐时间都会产生较大影响，是影响浮动曲线的重要参数，主要由导气装置性能决定。炮闩后坐时系统运动微分方程为：

式中，FT为输弹弹簧力：

Fs0为输弹弹簧预压力，Ks为输弹弹簧刚度系数，x2为炮闩位移。

自动机炮闩缓冲器为碟形弹簧式结构，炮闩后坐到位时通过炮闩缓冲器撞击炮箱，碟簧压缩储存部分能量，使得炮闩能够以一定速度复进。过程中系统存在能量损失，设1-ψ为损失能量，当炮闩缓冲器性能下降，即ψ减小时，会出现炮闩复进速度下降，复进用时增加，自动机击发点前移等现象。

分析自动机各阶段系统运动微分方程，结合各机构数据信息，计算连续发射过程中炮箱的浮动位移曲线如图2（a）所示。与实测的炮箱位移曲线图2（b）相比，计算出的浮动曲线基本能够反映出炮箱的运动规律，曲线中的炮弹击发点、自动机射弹周期及炮箱的二次后坐点也较为明显，可以作为自动机浮动曲线的特征量。

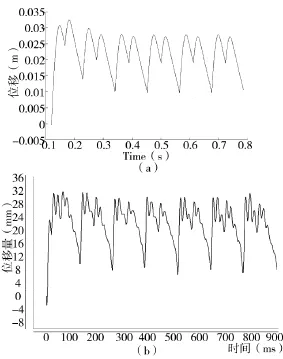
图2　炮箱浮动位移曲线

2　基于改进粒子算法的自动机状态评估

利用自动机各机构的性能信息能够得到自动机射击的浮动曲线，那么在实际中利用监测的浮动曲线评估自动机各机构的性能状态可以看作是其逆过程。在对自动机的动力学分析具有一定精度，以及对自动机浮动曲线的测量具有一定可靠度的基础上，尝试利用粒子群算法全局最优搜索的特点，结合浮动曲线特征量，对自动机内部相关机构及零件的性能状态进行评估。

在自动机连续射击过程中，每个机构的性能参数都对最终浮动曲线的形成产生一定作用，把各性能参数看作一个多维变量，则每个参数都可能在其自身范围内发生变化从而影响曲线的输出，因此，根据自动机浮动曲线进行状态评估的问题可视为根据实际浮动曲线输出结果，在一个多维的空间范围内寻找满足条件的各参数最优解。粒子群算法是一种基于群体智能的全局优化算法，其模拟社会的群体行为，在多维空间中构造粒子群进行寻优，每个粒子通过迭代过程中的群体和自身最优值修正自身前进的方向和速度。利用粒子群算法进行空间寻优，为各参数的性能评估提供一种可行的途径。

2.1标准粒子群算法

以自动机连续射击稳定状态下（第三发开始）的炮弹击发点位移XJ、自动机射弹周期Tp及炮闩的后坐时间TR为特征量，那么最优粒子应达到的目标是根据粒子内部各参数值，结合对自动机运动的分析，计算得出的曲线特征量应与实际曲线特征量最为一致。设自动机性能参数为炮闩后坐初速度Vc、浮动机弹簧预压力Ft0及炮闩缓冲器性能ψ，则由粒子i计算得到曲线特征量为：

目标函数设为：

标准粒子群优化算法步骤如下［3］：

①初始化惯性权重ω及加速度常数c1、c2，设置各维度参数的取值范围及粒子最大速度；

②随机生成n个m维粒子种群，即n个初始解Xi（t）及n各初始加速度Vi（t）；

③计算每个粒子的适应度S=f（Xi（t）），并寻找种群最优值pg；

④按照式（5）进行迭代，按照位置范围和速度上下限的要求更新每个粒子的位置Xi（t+1）及飞行速度Vi（t+1）。

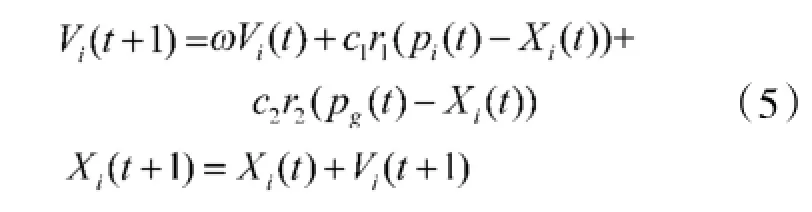
式（5）中r1、r2是［0，1］上均匀分布的随机数，pi为第i个粒子到目前为止所搜索到的最优位置，pg为整个群体中所有粒子搜索到的最优位置。

这种标准粒子群算法虽然操作简单，但算法存在后期收敛速度慢，经常在全局最优解附近提前完成收敛的现象［4］。为使算法具有更好的搜索速度和精度，针对其存在的缺陷，从惯性权重ω和后期粒子变异的方面对算法进行改进。

2.2非线性权值递减策略

惯性权重ω是粒子群算法中最重要的参数，较大的权值有利于提高算法的全局搜索能力，而较小的权值会增强算法的局部搜索能力［5］。文献［5］提出在算法早期通过加速惯性权值的递减来让算法较快地进入局部搜索，提高算法效率和后期收敛精度，由此本文通过构建凹函数递减权值对原有算法进行改进，即：

式中，c3为惯性权重的一个调节参数，不同的c3会使ω得到不同的下降效果。过大的c3会使算法过早进入局部搜索，而过小的c3会造成ω在结束迭代时变化不明显，失去改进效果，惯性权值随迭代次数的变化曲线如图3所示。

图3　权值随迭代次数下降曲线

2.3粒子变异替代

当在后期算法陷入局部最优且该局部最优处于种群最优时，改变惯性权重的方法无法使算法跳出局部最优状态。借鉴遗传算法中变异的思想，当种群最优值不发生变化或变化极小时，使种群中部分粒子发生变异并对变异结果选择性继承，帮助算法脱离局部最优的状态。设当种群最优适应度改变量小于Δ时，对种群进行以下两种变异操作：

①对适应度最差的后1/4粒子进行全局性的变异操作，即粒子每维度变量随机重新生成，并计算其新的适应度。若变异粒子适应度优于原粒子，则种群接受此次变异，若比原粒子适应度低，则保持原粒子状态；

②对适应度较好的粒子进行局部性的变异操作，即粒子每维度变量在当前位置附近进行随机生成，并计算其新的适应度。若变异粒子适应度优于原粒子，则种群接受此次变异，若比原粒子适应度低，则保持原粒子状态。

2.4结果分析

利用改进的粒子群算法，结合炮箱浮动曲线对自动机各性能进行评估。由图4可以看出，粒子群算法在寻优的过程中有较好的收敛性，但从收敛速度上来看，尽管标准PSO初始种群的平均适应度要明显优于改进PSO，但到后期仍然出现了收敛速度下降几乎停滞的现象，而变ω的PSO能够较快地进入局部搜索，具有良好的收敛速度；从最优解的结果上来看，如表1所示，利用粒子群算法结合曲线特征量，求得各机构性能参数的解与设置值基本吻合，但从精度上来看，经过变异和变ω的PSO得到的全局最优解明显优于标准PSO，经过变异的PSO与设置值最为接近，具有更好的精度，将这种方法应用于机构的状态参数评估上是有效可行的。

图4　种群平均适应度曲线

表1　算法结果对比

3　结论

本文为实现对某自行高炮自动机性能参数的准确评估，通过对自动机进行动力学分析，建立了自动机动力学模型，研究其连续射击过程中机构的运动规律及典型的浮动曲线。引入改进粒子群算法，结合浮动曲线特征量，对自动机性能参数进行全局寻优，算法在收敛速度和结果精度上相比于原有方法都有了显著提高，为自动机的状态参数评估提供了一种可行的方法。

参考文献：

［1］邱立军.武器装备故障预测与健康管理系统的关键技术［J］.舰船电子工程，2012，32（5）：17-18.

［2］郭竞尧，刘彦，李勇，等.某液压弹簧式浮动机仿真及优化［J］.液压与气动，2014（2）：85-87.

［3］郝云锁.基于SAPSO和改进SVM的风力发电机齿轮箱故障诊断系统研究［D］.上海：华东理工大学硕士学位论文，2014.

［4］高斐，李洪儒，许葆华.基于ICPSO优化的极限学习机在故障诊断中的应用［J］.中国机械工程，2013，24（20）：2753-2757.

［5］陈贵敏，贾建援，韩琪.粒子群优化算法的惯性权值递减策略研究［J］.西安交通大学学报，2006，40（01）：53-56.

［6］徐凤军，高跃飞，曹红松，等.某高炮自动机动力学仿真［J］.计算机仿真，2013，30（9）：14-17.

中图分类号：TJ35

文献标识码：A

文章编号：1002-0640（2016）04-0117-04

收稿日期：2015-03-15修回日期：2015-04-27

作者简介：孙致远（1990-），男，河南辉县人，硕士研究生。研究方向：武器性能检测与故障诊断。

Performance Assessment of Auto-mechanism Based on Improved PSO

SUN Zhi-yuan，ZHENG Jian，XIONG Chao，YIN Jun-hui
（Ordnance Engineering College，Shijiazhuang 050003，China）

Abstract：For the lack of effective method in the condition monitoring of the auto-mechanism of self-propelled anti-aircraft gun system，an approach of improved Particle Swarm Optimization（PSO）is introduced.Established the dynamic model of the auto-mechanism to simulate the recoil process and determined the characteristic quantity of the gun chest back curve to reflect the mechanical performance state，an approach of improved Particle Swarm Optimization（PSO）with better convergence and precision is proposed to evaluate the state parameters based on the curve characteristic quantity. The result shows the obvious advantage of the convergence and accuracy，and it achieves the state parameters assessment of auto-mechanism.

Key words：improved PSO，performance assessment，dynamics analysis