电驱动履带车辆带约束广义预测速度控制*

曾庆含，刘春光，魏曙光，马晓军

（1.装甲兵工程学院陆战平台全电化技术实验室，北京　100072；2.装甲兵工程学院，北京　100072）

电驱动履带车辆带约束广义预测速度控制*

曾庆含1，2，刘春光1，2，魏曙光1，2，马晓军1，2

（1.装甲兵工程学院陆战平台全电化技术实验室，北京100072；2.装甲兵工程学院，北京100072）

摘要：电传动履带车辆存在的参数非线性时变性强、惯量大，路面阻力容易受强扰动等特点，采用传统的PI控制容易产生较大的超调，降低暂态控制性能，传统的滑模控制算法难以克服常值扰动，消除稳态误差，易引起输出量剧烈抖振。针对上述问题，设计了广义预测速度控制器，结合电机饱和特性，对控制量进行了约束。仿真实验表明，所设计的控制算法能够克服系统参数非线性时变、路面扰动因素的影响，且跟踪准、响应快、超调小。

关键词：履带车辆，电驱动，速度，广义预测控制

0　引言

混合动力电驱动履带车辆，凭借燃油经济性好、机动性高以及静音行驶以及驱动部件布局灵活等突出优势［1-3］，逐渐成为履带车辆发展的重要方向，尤其是双侧式电驱动方案结构简单，控制方便，在电传动履带车辆中广泛采用［1-2］。由于驱动电机响应速度快、控制灵活，便于直接对车辆速度进行控制，能使车辆具备匀速巡航能力，降低驾驶员操控负担。电传动履带车辆作为电机负载具有惯量大的特点，速度调节时间较长，实际控制过程中容易产生超调，另外相比轮式车辆，履带车辆行驶环境恶劣，路面阻力系数、坡度等路面结构、参数的变化都会对车辆速度控制产生较大扰动，同时车辆振动较强往往存在较大测量噪声，还对算法的抗噪声能力要求较高，避免出现电机转矩的剧烈抖振。

要解决上述问题，传统控制方法如PID控制算法的鲁棒性、适应性差，难以车辆宽范围速度控制性能要求得到理想的效果。滑模控制具有响应快、鲁棒性好的特点，但同时也存在控制量抖振较大，难以抑制常值扰动等缺点。广义预测控制（Generalized Predictive Control，GPC）是一种自适应控制算法，采用多步预测、在线滚动优化和反馈校正等手段，能够有效处理模型失配问题，跟踪性能良好，对负载具有较强的适应性和鲁棒性。GPC的在线计算比较简单，不需要像神经网络、模糊控制等复杂的在线计算，可以提高系统的响应速度［4-5］。

本文以典型的双侧电驱动履带车辆为对象，开展速度控制算法研究，通过设计了广义预测控制速度控制算法，提高系统控制性能，仿真研究验证了速度控制算法的有效性。

1　车辆结构及动力学模型

双侧式电传动履带车辆结构如图1所示。发动机带动发电机发电，经整流后变为高压直流电，作为车辆主动力源，超级电容、高压蓄电池并联在直流母线上作为辅助动力源，二者共同提供驱动电机电能。车载运动控制器，根据驾驶员操控信号、反馈信号完成两侧驱动电机的目标转矩计算，通过总线将目标转矩信号实时发送至电机控制器。

图1　双侧式电传动履带车辆结构图

基于车辆动力学理论［6］，车辆行驶过程中除了受牵引力作用外，还受行驶阻力作用，主要包括滚动阻力、上坡阻力、空气阻力、加速阻力等。当车辆行驶在路面坡度为θ的硬路面上时，受力情况如图2所示。

滚动阻力为：

上坡阻力即车辆重力沿坡道方向上的分力为：

空气阻力为包括车辆行驶过程中所受的空气摩擦阻力和压力阻力，可用下式估算：

式中，CD为空气阻力系数，A为迎风面积，v为车辆行驶速度。其中A=σBH为车辆正面投影面积，B为履带中心距，H为全车高，σ为修正系数等于0.8～0.9。

加速阻力是车辆加速行驶时需要克服的惯性力：

式中，δ为车辆质量增加系数。

则可得车辆总得行驶总阻力为：

负载折合到电机轴上可得单台驱动电机负载转矩为：

式中，η金属履带的效率，经验公式为：

驱动电机系统动态方程［7］：

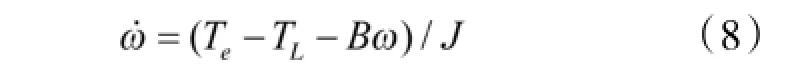
B为粘滞摩擦系数。

驱动电机转速为：

由于驱动电机的转矩响应时间为毫秒级，远小于车轮动态响应时间，算法设计中可忽略，设控制量为u，则有

式中，u为控制量。

2　广义预测控制算法设计

2.1系统的CARIMA模型

由驱动电机动态方程式（8）可推导出：

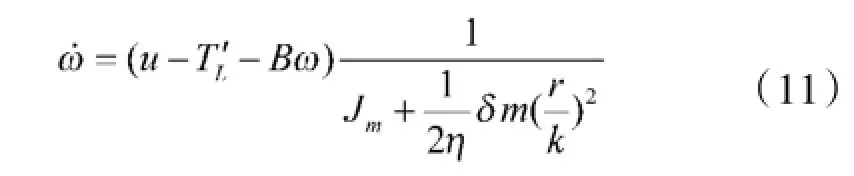
式中，

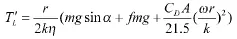
拉氏变换可得传递函数：

广义预测控制采用受控自回归积分滑动平均模型来描述受到随机干扰的对象。令Te（0）=0，ω（0）=0，TL=0，经过零阶保持以及Z变换后，得到系统的离散传递函数：

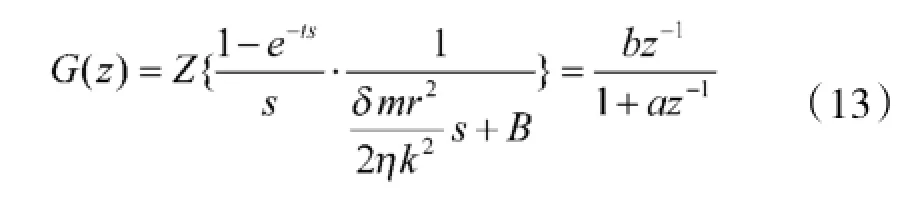
则系统CRAIMA模型为：

则CRAIMA模型［7］可改为：

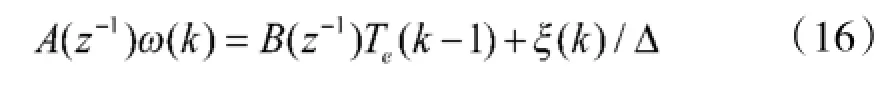
2.2广义预测控制律设计

建立电驱动系统的CRAIMA模型后，引入Diophantine方程：

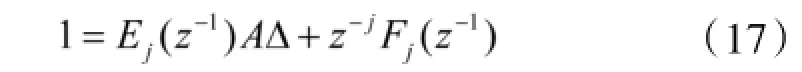
其中，Ej、Fj是由A（z-1）和预测长度j唯一确定的多项式

在式（16）两端乘EjΔzj以后可得

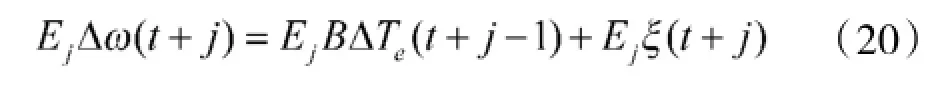
可以写出t+j时刻的输出量

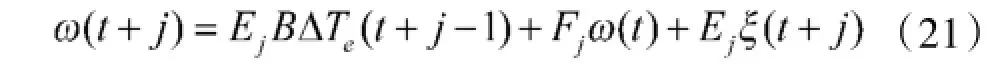
转化为向量形式，有

广义预测控制的目的是使被控对象的输出尽可能的接近给定值，因此，定义如下性能指标函数对控制效果进行约束。

式中，ω（rt）是输出量的给定值；N1、N2和Nu分别是最小、最大预测时域和控制时域；为控制加权常数。性能指标的第一项转速跟踪误差，第二项为控制量即电机输出转矩的增量。其中参数配置时，N1应大于对象的时滞数，N2应足够大，保证对象的动态特性能充分表现出来。若很小则系统稳定但ΔTe变化较大，导致系统执行机构磨损严重，同时降低驱动系统能量利用率［8］。在不考虑输入输出约束时，使性能指标最优的解可解析的表示为：

实际过程中，当输入给定超过执行机构即驱动电机的驱动能力物理限制时，容易导致广义预测控制算法给定控制量大幅变化，进入出现类似积分控制的深度饱和状态，使电机在加速或减速停止时超调量变大，系统暂态性能恶化，甚至导致系统不稳定，因此，需要对驱动电机输入给定进行如下约束。另外从提高系统能量利用率以及控制算法抗噪声能力的角度出发，应该对电机转矩变化率ΔTe进行限制［8］。

控制量Te幅值约束

2.3系统参数辨识

电传动车辆行驶过程中，由式（7）、式（12）可以看出系统参数随车辆行驶效率等因素呈现非线性变化，容易导致系统CARMA模型参数失配。自适应GPC在控制过程中，可以不断通过实际输入输出信息在线估计模型参数，并以此修正控制律。对象模型可以改为：

其中

利用渐消记忆法［9］的递推最小二乘法估计参数向量：

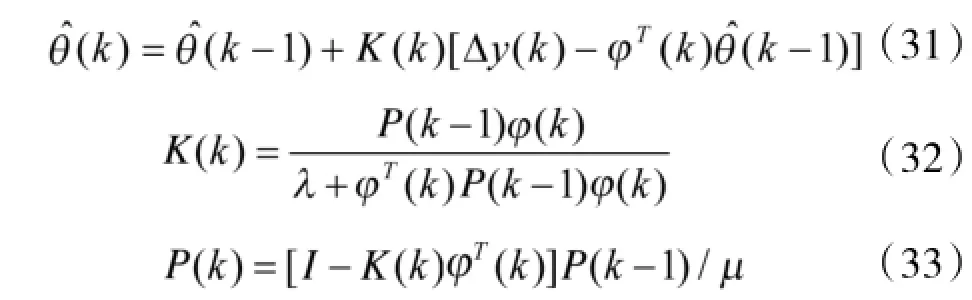
通过辨识得到多项式A（q-1）、B（q-1）的参数后，就可计算得出控制律中的dT、f，进而求出最优控制律。

综上所述系统控制结构如图3所示。

图3　系统控制结构框图

3　仿真实验

为了验证本文所提出的控制算法的有效性，基于Matlab软件建立了仿真模型。车辆采总重量M=8 000 kg。驱动电机性能参数：pn=6，J=0.021 kg·m2，R=4.5mΩ，Ld=0.47mH，Lq=1.45mH，额定功率100 kW，额定转速3 200 r/min，额定转矩300 Nm，最大转矩625 Nm。路面阻力系数设为0.05，考虑到实际测量信号存在的噪声，反馈信号增加幅值0.2，50 Hz的随机噪声。

GPC控制器，参数设置为 N1=1、N2=80和 Nu=30，=0.015，采样周期0.01，取遗忘因子μ=0.995，参数辨识初始值为（0）=0，P（0）=105I［10］。为验证控制器的性能与PI控制算法、滑模控制算法SMC进行了对比实验，其中 PI控制器参数 kp=250、ki=12，算法滑模边界层厚度均为ε=0.7，切换项增益β1=625。

3.1加、减速工况实验

图4为车辆行驶速度控制曲线，图5为电机输出转矩曲线。如图5所示，0 s时期望速度30 km/h，10 s时期望速度上升为60 km/h，30 s时期望速度减为10 km/h，40 s时期望速度上升为40 km/h，其中路面默认设置为水泥硬路面。

由仿真结果可看出，GPC、SMC控制算法跟踪效果较为理想，而PI控制算法则跟踪时间较长的过程中出现较大的超调现象，暂态性能较差，同时滑模控制时电机输出转矩存在较强的抖振现象，相比之下GPC控制效果最优。

图4　行驶速度曲线

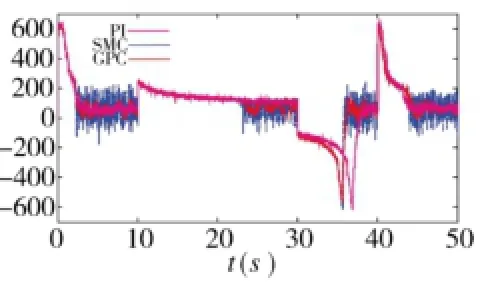
图5　电机输出转矩曲线

3.2鲁棒性实验

图6为车辆行驶速度控制曲线，图7为电机输出转矩曲线。如图5所示，0 s时期望速度30 km/h，10 s时期望速度下降为10 km/h，其中6 s～8 s内水平路面行驶阻力系数阶跃变化为0.1，模拟路面小扰动情况，13 s～17 s内路面坡度变为30°，模拟路面大扰动情况。

由仿真结果可看出，3种控制算法均能抑制路面小扰动，但路面大扰动时，PI控制抗扰性能明显较差，车速出现大幅跌落，而滑模控制侧出现稳定的静差，而GPC控制算法则能实现对扰动的抑制，实现精确跟踪。由此可见，GPC控制算法能够抑制不确定扰动的影响，对控制模型失配具有较强的鲁棒性，能够实现速度的精确跟踪。

图6　行驶速度曲线

图7　电机输出转矩曲线

4　结论

（1）针对电驱动履带车辆速度控制存在的惯量

大易产生超调、扰动强容易出现模型失配等问题，建立了车辆驱动系统的CARIMA模型，设计了自适应广义预测控制算法，为改善控制动态性能，算法设计引入了控制量幅值和增量的约束。

（2）与传统PI、滑模控制等控制算法相比，具有响应快、超调小、抗扰能力强的优点，以及输出控制量平滑，能够提高电驱动车辆能量利用率，能够实现对电传动履带车辆良好速度控制。

参考文献：

［1］李剑.混合动力履带车辆制动控制策略研究［D］.北京：北京理工大学机械与车辆工程学院，2009：13-14.

［2］孙逢春，陈树勇，郭汾.基于转矩控制策略的电传动履带车辆驱动特性研究［J］.兵工学报，2007，28（2）：129-133.

［3］GAI J T，MA T.Research on a novel type of hybrid propulsion system and control strategy for tracked vehicle［C］//International Conference on Electrical and Control Engineering. 2010：4066-4069.

［4］席裕庚，预测控制［M］.北京：国防工业出版社，2013.

［5］王伟.广义预测控制理论及其应用［M］.北京：科学出版社，1998.

［6］王良曦，王红岩.车辆动力学［M］.北京：国防工业出版社，2008.

［7］王国良.永磁同步电动机广义预测控制的研究［D］.天津：河北工业大学，2004.

［8］金鸿章，张晓飞，李冬松，等.零航速减摇鳍永磁同步电机伺服系统广义预测控制［J］.中国电机工程学报，2008，12（25）：87-92.

［9］陈书锦，李华德，马保柱，等.电动汽车驱动系统广义预测控制［J］.电机与控制学报，2006，10（6）：110-114.

［10］薛定宇.控制系统计算机辅助设计——Matlab语言与应用［M］.3版.北京：清华大学出版社，2012.

中图分类号：TP81

文献标识码：A

文章编号：1002-0640（2016）04-0057-04

收稿日期：2015-04-05修回日期：2015-04-24

*基金项目：国防科技创新工程基金资助项目（12050005）

作者简介：曾庆含（1988-），男，湖北钟祥人，博士研究生。研究方向：车辆电传动控制技术。

Constrained Generalized Predictive Velocity Control of Electric Drive Tracked Vehicle

ZENG Qing-han1，2，LIU Chun-guang1，2，Wei Shu-guang1，2，MA Xiao-jun1，2
（1.Laboratory of All-electrization Technology for Ground Combat Platform，Academy of Armored Force Engineering，Bejing 100072，China；2.Academy of Armored Force Engineering，Bejing 100072，China）

Abstract：The velocity control of electrical drive tracked vehicle has characters of time-vary nonlinear parameters，large inertia and strong road disturbance.So the traditional PI control may lead obvious overshoot which will decrease transient performance，and SMC could not eliminate track error brought by stable disturbance and may lead significant chattering.To overcome those problems，generalized predictive velocity controller is developed which's control output is constrained considering motor saturation and drive efficiency.Simulation results demonstrated that control algorithm is robust to time-vary nonlinear parameters and road disturbance，and could track target value rapidly and precisely with little overshoot.

Key words：tracked vehicle，electric drive，velocity control，GPC