极限弹性性能的材料微结构拓扑优化设计
张 严 杜义贤,2 杜大翔 田启华
(1. 三峡大学 机械与动力学院, 湖北 宜昌 443002; 2. 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌 443002)
极限弹性性能的材料微结构拓扑优化设计
张严1杜义贤1,2杜大翔1田启华1
(1. 三峡大学 机械与动力学院, 湖北 宜昌443002; 2. 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌443002)
摘要:基于应变能等效的能量法,求解材料微结构的等效弹性系数矩阵,以等效弹性系数矩阵主对角线上元素的某项或某几项的加权组合最大为目标,以材料体积率为约束,构建具有极限弹性性能材料微结构的拓扑优化模型,采用SIMP插值结合优化准则法求解该优化模型,推导了优化求解过程中的敏度表达式,实现了具有极限弹性性能的材料微结构拓扑构型设计.数值算例验证拓扑优化模型和算法的有效性.
关键词:能量法;材料微结构;极限弹性性能;拓扑优化;SIMP插值
高科技的发展对材料性能提出了越来越高的要求,如零或负的膨胀系数、极端热传导系数、负泊松比等特殊的性能.材料的宏观性能依赖于材料微观结构的性能,而材料微观结构的性能取决于微观结构的尺度、构型及材料组份比,因此,对具有特殊宏观性能的材料可以通过对其微观结构的设计来实现[1].国外学者如Sigmund等[2]率先提出材料微结构拓扑优化理论,对各向同性材料微结构单胞采用拓扑优化逆向设计技术实现了工程中所需材料特定宏观性能的微结构构型设计,Neves等[3]基于均匀化方法获得了周期性线弹性微结构的最优拓扑构型,James等[4]通过对具有最大刚度和流体渗透性的微结构进行设计,实现了材料多功能优化,Huang等[5]基于双向渐进结构优化法实现了具有最大剪切模量和最大体积模量的微结构拓扑优化.国内学者如刘远东等[6]基于多尺度均匀化方法开展了周期性复合材料微结构的多目标拓扑优化设计,王宝来等[7]针对轻质材料利用拓扑优化技术实现了最刚微结构构型设计,王宪杰等[8]利用双向渐进结构优化方法实现了基于宏观性能的微观多孔材料拓扑优化设计,汪雷等[9]基于均匀化理论和拓扑优化技术实现了具有最优导热性能的复合材料微结构拓扑优化设计,张卫红等[10]基于能量法实现了材料微结构的等效弹性性能的预测,采用对偶凸规划方法结合周长约束策略进行了微结构构型优化设计.拓扑优化的目的就是确定具有特定性能微观结构的材料分布,充分发掘材料潜力,从设计的角度提高材料性能.
基于此,本文采用应变能等效的能量法实现材料微结构的等效弹性系数矩阵的求解,然后以等效弹性系数矩阵主对角线上元素的某一项或者某几项的加权组合为目标,以材料体积率为约束,建立材料微结构的拓扑优化模型.采用SIMP插值及优化准则法求解该优化模型,以敏度过滤抑制数值不稳定现象,实现具有极限弹性性能的最优微结构的拓扑构型优化设计.
1材料微结构的等效性能预测
均匀化方法具有严格的数学理论推导,以连续介质理论为基础,基于扰动理论将物理场按表征微观结构尺度的小参数渐进展开,从而得到材料微结构的等效弹性性能,但其数学推导繁琐,计算复杂.基于应变能等效的能量法与均匀化方法相比,其本质相同,但其计算效率高,推导简洁,编程实现简便[10],因此本文将通过应变能等效的能量法求解材料微结构的等效弹性性能.

图1 微结构等效示意图
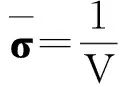
(1)
式中,DH即为微结构的等效弹性系数矩阵.
对于二维正交各向异性材料,式(1)可进一步表示为
(2)

定义微结构的应变能为
(3)
在均匀边界载荷条件下,材料微结构和均质等效体的弹性应变能应是相等的,由此可得出微结构的单位体积应变能
(4)
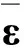

表1 给定工况条件下微结构的应变能
由表1可得材料微结构的等效弹性系数矩阵DH的表达式为
(5)
2材料微结构的拓扑优化模型
基于SIMP插值模型,以单元的相对密度为设计变量,结构整体的体积率为约束,材料微结构的某一项或某几项极值力学特性为目标,建立如下优化数学模型:
(6)
式中,ωl为加权系数(ωl∈[0,1]);Dll为等效弹性系数矩阵DH的主分量(其中ll=11、ll=22、ll=33分别对应为D1111、D2222、D1212);V(ρ)为优化后结构的体积;f为体积系数;V0为设计域体积;为防止刚度阵奇异,取最小密度值ρmin=0.001.
3灵敏度分析
有限元平衡方程为
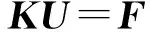
(7)
式中,F、U分别为微结构的结点力向量与结点位移向量.
见表1,在相应边界条件下(上标n表示边界条件)的材料微结构应变能为
(8)
由式(7)、(8)可得微结构的应变能对设计变量ρi的导数为
(9)
其中
(10)
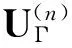
由式(5)得
(11)
按照上述灵敏度的求解方法,结合有限元分析,采用优化准则求解算法即可对上述优化模型进行优化求解,优化流程如图2所示,其具体步骤如下:
Step1:定义材料微结构设计域,将材料离散到单元;
Step2:材料微结构有限元静力分析;
Step3:基于能量法求解材料微结构的等效弹性系数矩阵;
Step4:目标函数的计算及敏度分析;
Step5:采用优化准则法对设计变量进行更新;
Step6:根据收敛条件判断目标函数是否收敛,如果不满足收敛条件,则重复Step2~Step5,如果满足收敛条件,输出结果.
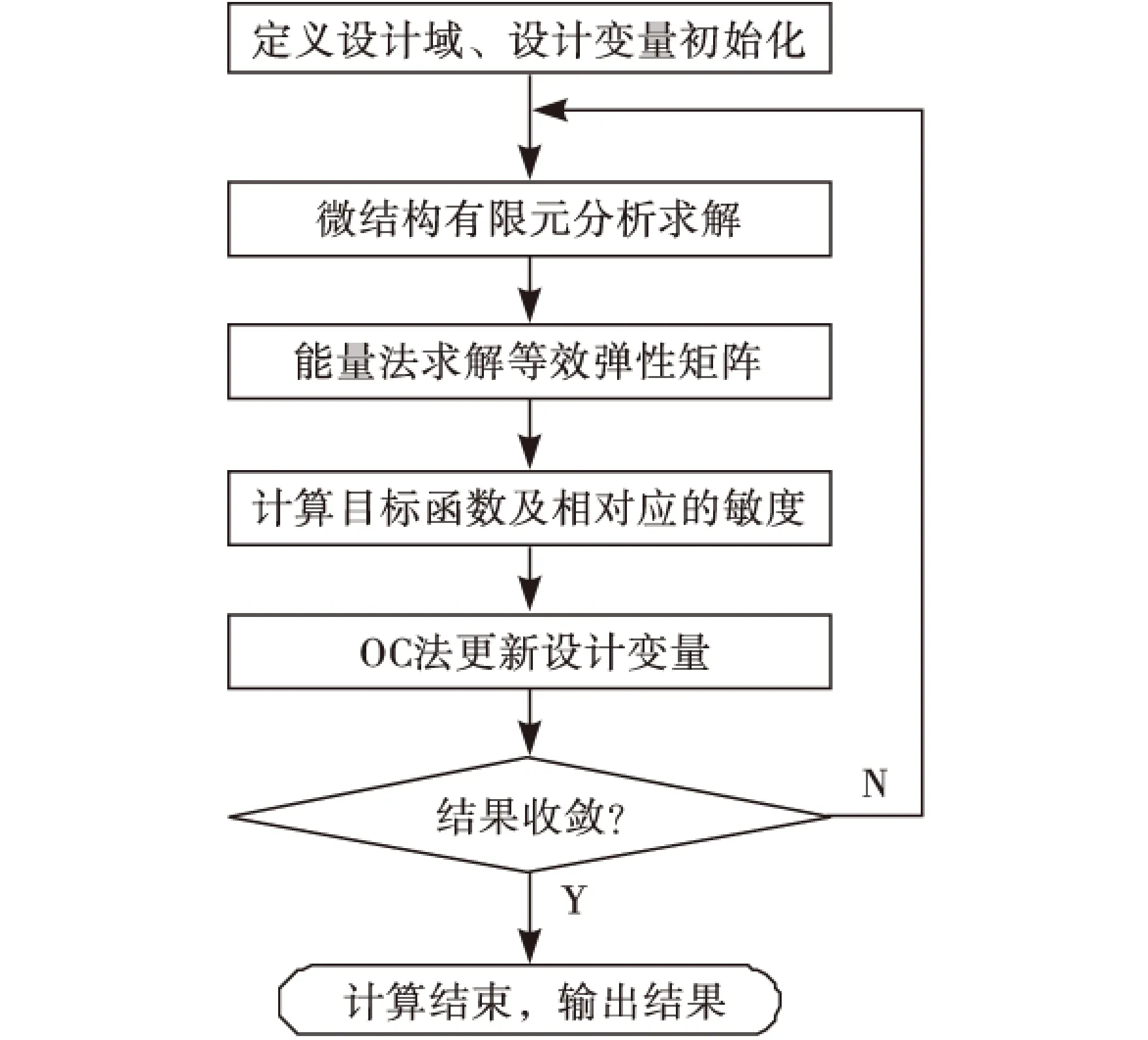
图2 材料微结构优化设计流程图
4数值算例及分析
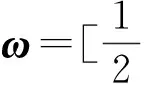

表2 不同优化目标下微结构的最优拓扑构型
由表2可知:
5结语
本文基于应变能等效的能量法求解材料微结构的等效弹性矩阵,以等效弹性矩阵主对角线上元素的某项或者某几项加权组合最大为目标建立优化模型对微结构进行拓扑优化设计.算例分析表明,采用SIMP插值和优化准则法有效求解了该拓扑优化问题,利用敏度过滤消除了数值不稳定现象,并得到了具有最优水平方向抗拉强度、竖直方向抗拉强度、抗剪切强度和双向抗拉强度等极限弹性性能的微结构拓扑构型.
参考文献:
[1]Kim Y Y, Yoon G H. Multi-resolution Multi-scale Topology Optimization-a New Paradigm[J]. International Journal of Solids and Structures, 2000, 37(39):5529-5559.
[2]Sigmund O. Materials with Prescribed Constitutive Parameters:An Inverse Homogenization Problem[J]. International Journal of Solids and Structures, 1994, 31(17):2313-2329.
[3]Sigmund O, Torquato S. Design of Materials with Extreme Thermal Expansion Using a Three-phase Topology Optimization Method[J]. Journal of the Mechanics and Physics of Solids, 1997, 45(6):1037-1067.
[4]James K, Jeam H. Optimizing Multifunctional Materials:Design of Microstructures for Maximized Stiffness and Fluid Permeability[J]. International Journal of Solids and Structures, 2006, 43(22):7028-7047.
[5]X Huang, A Radman, Y M Xie. Topological Design of Microstructures of Cellular Materials for Maximum Bulk or Shear Modulus[J]. Computational Materials Science, 2011, 50(6):1861-1870.
[6]刘远东,尹益辉,胡文军.周期性复合材料微结构的多目标拓扑优化设计[J].机械强度,2012,34(4):527-530.
[7]王宝来,温凤春,梁军.轻质材料微结构构型的拓扑优化设计[J].哈尔滨工业大学学报,2009,41(1):76-79.
[8]王宪杰,张洵安.基于宏观性能的微观多孔材料拓扑优化[J].功能材料,2014,45(18):18078-18082.
[9]张卫红,汪雷,孙士平.基于导热性能的复合材料微结构拓扑优化设计[J].航空学报,2006,27(6):1229-1233.
[10] Zhang Weihong, Wang Fengwen, Dai Gaoming, et al. Topology Optimal Design of Material Microstructures Using Strain Energy-based Method[J]. Chinese Journal of Aeronautics, 2007, 20(4):320-326.
[责任编辑张莉]
收稿日期:2016-01-21
基金项目:湖北省杰出青年基金资助项目(No.2013CFA022);湖北省科技支撑计划对外科技合作资助项目(No.2015BHE026)
通信作者:杜义贤(1978-),男,副教授,博士,研究方向为CAD/CAM技术,结构优化与分析.E-mail:duyixian@aliyun.com
DOI:10.13393/j.cnki.issn.1672-948X.2016.02.016
中图分类号:TH122:TB34
文献标识码:A
文章编号:1672-948X(2016)02-0071-04
Topology Optimization for Material Microstructures with Extreme Elastic Properties
Zhang Yan1Du Yixian1,2Du Daxiang1Tian Qihua1
(1. College of Mechanical & Power Engineering, China Three Gorges Univ., Yichang 443002, China; 2. Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges Univ., Yichang 443002, China)
AbstractBased on the strain energy equivalent energy method, the equivalent elastic coefficient matrix of the materials microstructure is to solve. With the goal of maximizing the one or several of the weighted combination of the leading diagonal elments in the equivalent elastic coefficient matrix, to the material's volume rate as the constraint, the topology optimization model for the material microstructures with extreme elastic properties is constructed. The SIMP interpolation and optimality criteria method are used to solve the optimization model; and then the sensitivity expression in the process of optimization solution is derived. Finally, the topological configuration of material microstructures with extreme elastic properties is achieved. Some numerical example verifies the validity of the topology optimization model and algorithm.
Keywordsstrain energy-based method;material microstructure;extreme elastic properties;topology optimization;SIMP interpolation

