基于改进Kelvin模型的三维蠕变损伤模型研究

吴祝林　王　伟　朱鹏辉　陈　曦

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室，南京　210098； 2. 河海大学 岩土工程科学研究所， 南京　210098)



基于改进Kelvin模型的三维蠕变损伤模型研究

吴祝林1，2王伟1，2朱鹏辉1，2陈曦1，2

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室，南京210098； 2. 河海大学 岩土工程科学研究所， 南京210098)

摘要：岩石在长时间的蠕变发展中，会呈现出不同的阶段性特性，开始表现为衰减蠕变，蠕变速率逐渐减小，紧接着保持稳定的蠕变速率呈现稳定蠕变发展，最后外界应力超过屈服应力导致加速蠕变．常用的元件模型只能有效地模拟衰减和稳定蠕变阶段，加速蠕变特性则需要引进非线性特性的元件模型或是损伤理论，本文引进损伤理论和损伤元件，与常用元件组合模型串联组合，即可模拟出全过程的岩石蠕变特性，通过引进弹塑性损伤元件和Kelvin元件模型，建立了三维改进的Kelvin蠕变损伤模型，并推导了三轴压缩下岩石的轴向应变方程，用砂岩蠕变试验数据拟合出模型参数．建立的模型参数较少，易于确定，而且推导的三维模型更能真实的反应岩石在自然界中的应力状态．

关键词：加速蠕变；损伤理论；弹塑性损伤；轴向应变

岩石流变[1-2]是岩石学科中重要的一块内容，在理论上它不仅反应了岩石的力学特性，包括变形特性、强度特性等，而且也与岩石工程问题的长期稳定性密切相关．目前国家的许多工程问题都需要研究岩石的流变特性，如隧道工程、边坡工程等，因此，有效掌握岩石的流变特性，有助于降低工程成本、减少工程事故．现有的流变模型大多数是基于一维的，不能有效地反应岩石自然界中处于三维应力状态的真实情况，如何构建三维应力状态的且参数较少的流变模型，正是本文研究的重点．

目前流变模型[3-4]大致是基于经验模型、元件模型、损伤理论构建的[5-8]．然而这些模型大多数是只考虑一维情况的，自然界中的岩体基本处于三维应力下，因此有必要将一维蠕变方程推导成三维，探讨三维的蠕变模式，且这些模型能够描述加速蠕变阶段的也不多．在前人对加入蠕变阶段的研究中，较多的是先引进非定常参数，进而建立蠕变模型．范庆忠[9]在元件组合模型中用非线性损伤变量代替了Burgers中的线性部分，且有效地模拟了软岩的三阶段蠕变特征，且继续在文献[10]中采用了损伤和硬化的两种机制来描述非线性损伤部分，模拟的试验曲线有效验证了模型的合理性；陈卫忠[11]建立的非线性蠕变方程是考虑了粘滞系数的影响，且将推导的蠕变速率与试验蠕变速率对比分析，表明盐岩非线性蠕变模型的有效性．朱昌星[12]以锦屏二级水电站为例，考虑时效损伤和加速门槛值的特征，建立了包含加速蠕变在内的三阶段蠕变损伤方程．张强勇[13]则将岩石蠕变方程中的参数看做是非定常的，且参数随着蠕变时间而弱化，也有效的建立了蠕变方程，并继续推导了三维差分形式．然而，这些建立的蠕变模型大多数都是基于一维情况，缺少三维模型的形式，且模型参数较复杂，自然界中的应力更是处于三维应力状态下，因此有必要在简单模型参数的情况下继续推导出三维蠕变模型形式．本文在简单的Kelvin本构模型中引入弹塑性损伤体来描述加速阶段特性，并将整个模型推导成三维形式，通过砂岩蠕变试验数据拟合求出参数，参数少，易于拟合，这是简单蠕变模型的一个优点，最后，用试验数据蠕变曲线对比分析模型理论曲线，吻合度较好，表明推导的三维模型较为合理．

1流变本构模型的建立

1.1改进的Kelvin一维本构模型

引进曹文贵[14]对岩石蠕变过程的研究，将岩石蠕变方程看作是线性阶段和加速阶段的组合，其中，用弹塑性损伤体来描述模型中的加速阶段，线性阶段则用基本流变元件Kelvin元件模拟，由此组合的岩石蠕变模型既能描述线性阶段，当外界应力超过岩石屈服应力时，又能描述加速阶段．串联组合的岩石蠕变模型如图1所示，弹塑性损伤体用来模拟加速蠕变阶段，Kelvin元件模型则有效模拟减速蠕变阶段，当外界应力小于屈服应力σs时，只产生Kelvin体应变εve，当外界应力超过岩石屈服应力σs时，损伤体起作用，产生加速蠕变，即岩石总应变ε为弹塑性损伤体应变εep和Kelvin体应变εve的叠加．

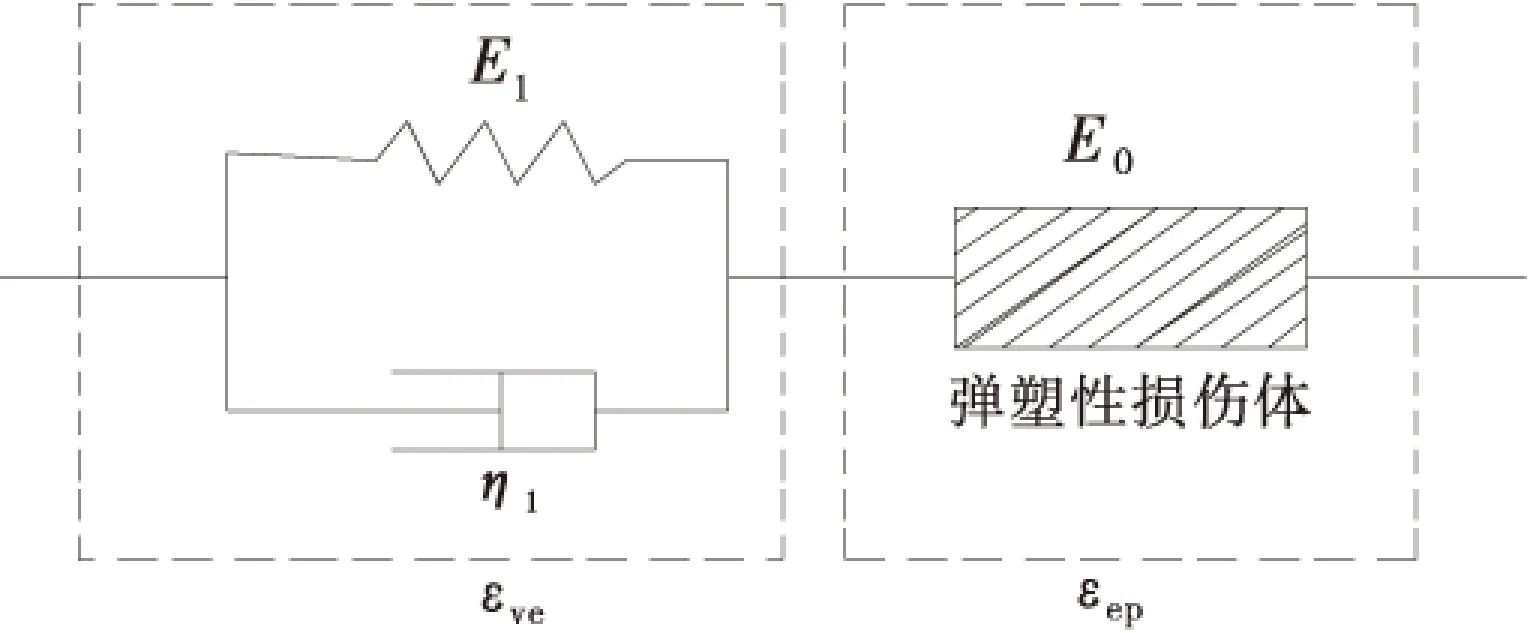
图1　岩石蠕变模型

Kelvin体的粘弹性应变 如下式[15]：

(1)

弹塑性损伤体本构模型如下式[14]：

(2)

由式(1)、(2)可得岩石一维状态下的全过程蠕变方程：

(3)

引入开关函数〈σ0〉，并令：

(4)

(5)

由上式可知该蠕变模型方程有如下特点：

1)如果岩石出现加速蠕变阶段，即σ0≥σs及〈σ0〉=1，则当t→tF，ε→∞且dε/dt→∞，显然，该模型能反应岩石加速蠕变阶段特征．

2)如果岩石不出现加速蠕变阶段即σ0<σs及〈σ0〉=0，上式可写成：

(6)

可见，该蠕变模型能够反映初期蠕变特征

1.2三维本构模型推导

改进的Kelvin模型三维应力示意图如图2所示．图中，GM为弹塑性损伤体的剪切模量，GK为Kelvin体的剪切模量，HK为Kelvin体的粘滞系数，sij为偏应力张量，相应的偏应变张量为eij，通过下式计算：

（1）这样在其中一组数前加负号，则两组数的和为0。这样的问题可归纳为找到几个和为18的数。（2）找到了一组和为18的数，则余下的数和必为18，这两数具有对偶性，在任一组数前加负号，它们的和都为0。（3）在8个数中，添加负号的数至少为3个，至多为5个，（因为8+7+3=18,1+2+3+4+8=18），循着规律去分析，大家终于得出这一问题的所有答案。

图2　改进Kelvin模型三维示意图

(7)

(8)

由Kelvin体可求得其偏应变方程：

(9)

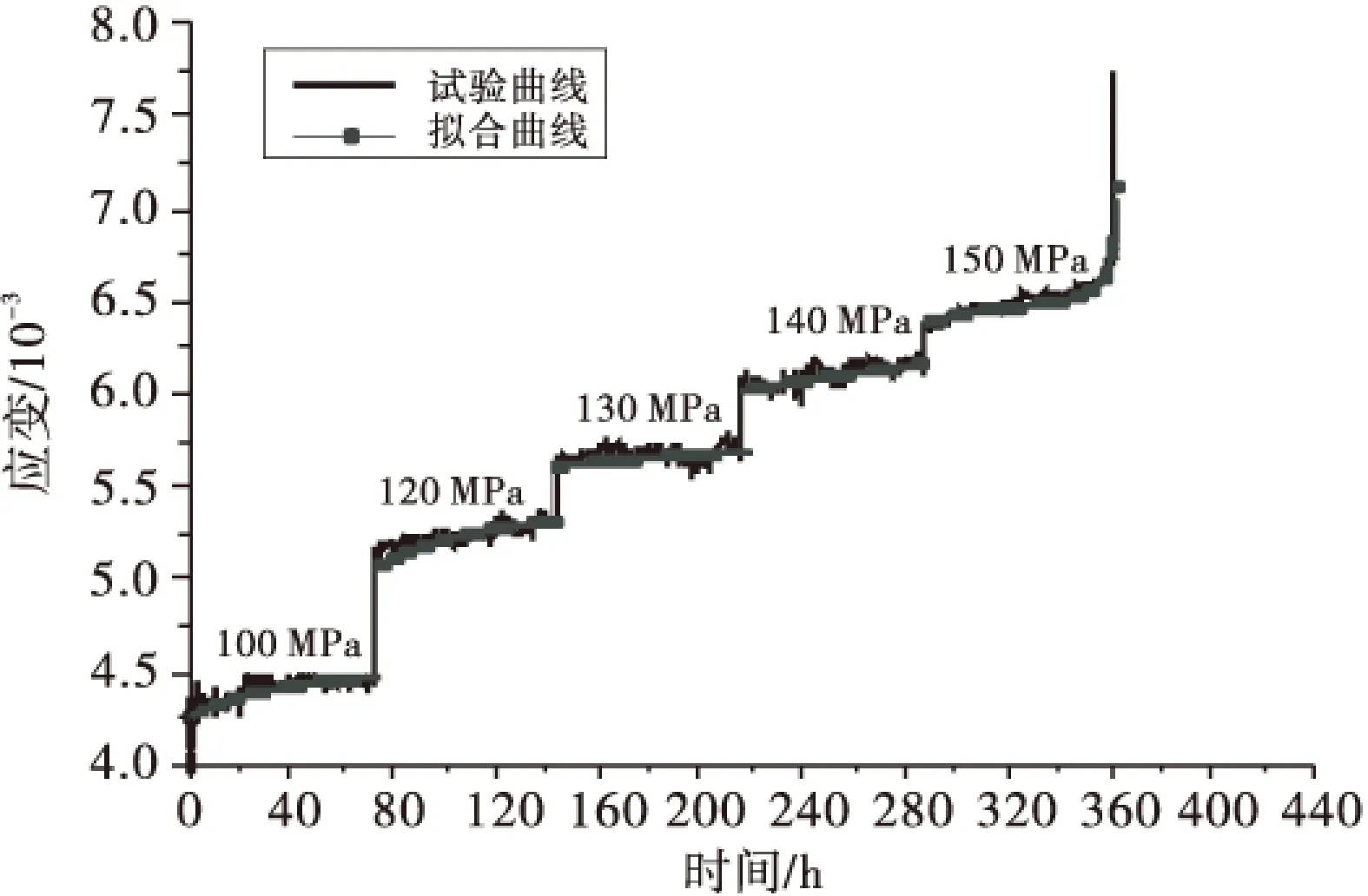
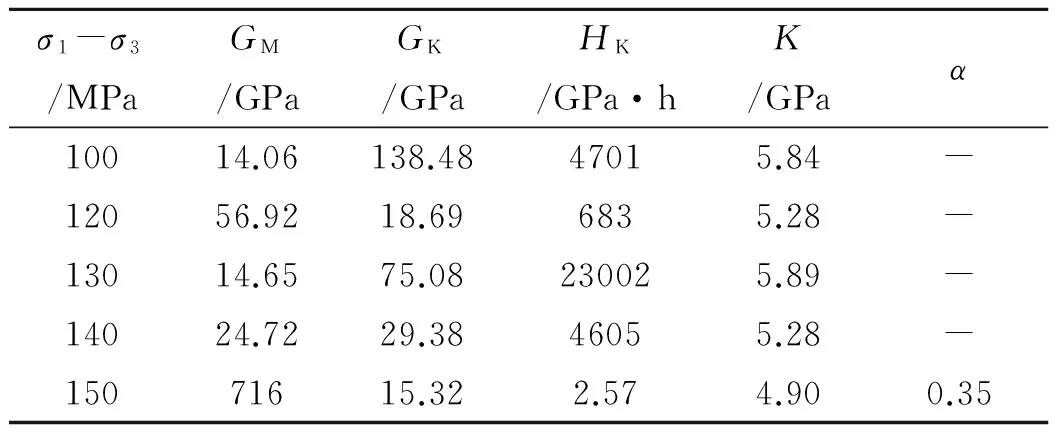
弹塑性损伤体在未受损(即偏应力小于屈服偏应力s1-s3

(10)

联立式(8)～(10)可得建立的三维模型蠕变方程：

(11)

对于损伤变量D，引进文[14]对损伤变量的定义，即：

(12)

式中，tF为岩石从开始蠕变到蠕变破坏的总时间．代入式(11)得：

(13)

此即为改进Kelvin模型的三维蠕变方程．

当试样处于三轴压缩时，其应力状态特征为

(14)

其轴向应变可表示为

(15)

不考虑塑性体积应变和和体积流变应变，即εvp=εvc=0，则式(15)变为

(16)

在岩石三轴压缩试验过程中，先施加围压，再读取产生的应变，因此相应产生的应变为

(17)

由上几式可推导得到试样三轴压缩状态下的轴向应变ε为

ε=

(18)

2模型参数的确定

由建立的模型可知，该模型共有GM、GK、HK、tF、α 5个参数，其中tF为岩石蠕变寿命，可根据蠕变试验曲线岩石的破坏时间来确定，另4个参数可根据试验曲线拟合得到，参数较少，易于拟合．

引进王伟[16]的砂岩在3MPa围压条件下的蠕变试验曲线，如图3所示．由试验曲线可知，砂岩的蠕变过程经由试验曲线可知，砂岩的蠕变过程历了初始蠕变阶段、稳定蠕变阶段和加速蠕变阶段，在围压3MPa条件下，100MPa应力作用下，出现了瞬时弹性变形，150MPa应力作用下，由于超过了砂岩的屈服应力，因此出现了加速蠕变阶段，直至砂岩损伤破坏．

图3　围压3 MPa条件下砂岩蠕变试验曲线

本文基于一维蠕变方程的基础上，推导出三维蠕变方程，通过引入蠕变试验数据[16]，拟合蠕变方程，求出各级应力状态下的三维模型参数，见表1，并将试验曲线与三维模型理论曲线对比分析，两者吻合完好，如图4所示．从图4可以看出，该蠕变模型不仅能很好模拟前期的初始蠕变和等速蠕变阶段特征，而且还能很好的描述当外界应力超过屈服应力的加速蠕变阶段特征．由此可以验证本文改进三维蠕变模型的合理性．由于在此基础上拟合求出的模型参数是针对砂岩在3MPa围压下得出来的结果，对于其他岩样或是不同围压作用下该模型的有效性如何，还需做进一步的试验研究．

图4　围压3 MPa条件下三维蠕变模型理论曲线与试验曲线对比

σ1-σ3/MPaGM/GPaGK/GPaHK/GPa·hK/GPaα10014.06138.4847015.84-12056.9218.696835.28-13014.6575.08230025.89-14024.7229.3846055.28-15071615.322.574.900.35

3结论

本文在前人研究的基础上，引入弹塑性损伤体描述加速蠕变阶段，与描述线性阶段的Kelvin体组合，在一维的基础上推导出三维模型．得到以下结论：

1)Kelvin体能有效的模拟岩石线性阶段过程，对于非线性阶段，通过引入损伤变量，构建损伤演化方程．将引进的弹塑性损伤体与Kelvin体串联组合，有效的模拟了在各级应力作用下岩石的全过程蠕变过程，即从较小的初始应力下的初始蠕变和稳定蠕变阶段，到应力等级逐渐增大而产生的加速蠕变阶段．

2)大多数蠕变方程都是基于一维的，本文在一维的基础上推导出三维蠕变方程，建立了反映蠕变损伤的三维蠕变本构方程，该三维蠕变本构形式简单，参数易于确定，更适宜推广．

3)通过对砂岩三轴压缩蠕变试验曲线的模拟，拟合出各级应力状态下的模型参数，包括其中的加速蠕变阶段，对比分析理论曲线与试验曲线的吻合度，可表明建立的三维蠕变方程不仅能反应初始蠕变阶段和稳定蠕变阶段，更能有效的反应加速蠕变阶段，从而验证了本文三维蠕变损伤模型的合理与有效性．

参考文献：

[1]孙钧．岩土材料流变及其工程应用[M]．北京：中国建筑工业出版社，1999．

[2]穆霞英．蠕变力学[M]．西安：西安交通大学出版社，1990．

[3]Griggs D T． Creep of rocks[J]． Journal of Geology，1939， 47： 225-25．

[4]Fujll Y ， K yama T , Ishijima Y , et al. Circumfer entail Strain Behavior During Creep Tests of Brittle Rocks[J]． International Journal of Rock M echanics and Mining Sciences, 1999, 36( 3) ： 323- 337．

[5]范广勤．岩石工程流变力学[M]．北京：煤炭工业出版社，1993．

[6]余寿文．损伤力学[M]．北京：清华大学出版社，1997．

[7]李兆霞．损伤力学及其应用[M]．北京：煤炭工业出版社，1993．

[8]李灏．损伤力学基础[M]．济南：山东科学技术出版社，1992．

[9]范庆忠，高延法，崔希海，等．软岩非线性蠕变模型研究[J]．岩土工程学报，2007，29(4)：505-509．

[10] 范庆忠，高延法．软岩蠕变特性及非线性模型研究[J]．岩石力学与工程学报，2007，26(2)：391-396．

[11] 陈卫忠，王者超，伍国军，等．盐岩非线性蠕变损伤本构模型及其工程应用[J]．岩石力学与工程学报，2007，26(3)：467-472．

[12] 朱昌星，阮怀宁，朱珍德，等．岩石非线性蠕变损伤模型的研究[J]．岩土工程学报，2008，30(10)：1510-1513．

[13] 张强勇，杨文东，张建国，等．变参数蠕变损伤本构模型及其工程应用[J]．岩石力学与工程学报，2009，28(4)：732-739．

[14] 曹文贵，袁靖周，王江营，等．考虑加速蠕变的岩石蠕变过程损伤模拟方法[J]．湖南大学学报：自然科学版，2013，40(2)：16-20．

[15] 蔡美峰，何满潮，刘东燕．岩石力学与工程[M]．北京：科学出版社，2006．

[16] 王伟，吕军，王海成，等．砂岩流变损伤模型研究及其工程应用[J]．岩石力学与工程学报，2012，31(2)：3651-3658．

[责任编辑周文凯]

收稿日期：2016-01-08

基金项目：国家重点基础研究发展973项目(2011CB013504)；留学回国人员科研启动基金(51103312)

通信作者：吴祝林(1990-)，男，硕士，从事岩石力学与工程方面研究．E-mail：1206725293@qq.com

DOI：10.13393/j.cnki.issn.1672-948X.2016.02.007

中图分类号：TU45

文献标识码：A

文章编号：1672-948X(2016)02-0029-04

Research on Three-dimensional Creep Damage Model Based on Improved Kelvin Model

Wu Zhulin1,2Wang Wei1,2Zhu Penghui1,2Chen Xi1,2

(1. Key Laboratory of Ministry of Education for Geotechnic & Embankment Engineering , Hohai Univ., Nanjing 210098, China; 2. Geotechnical Research Institute, Hohai Univ., Nanjing 210098, China)

AbstractRock creep will present different phased characteristics in the long time creep developing; it begins to show the attenuation creep, creep rate decreasing, and then keeps steady creep development in a stable creep rate; finally it evolves to accelerated creep after the external stress exceeding yield stress. Common component model can only effectively simulate the attenuation and stable creep stage; accelerated creep properties require the component model or damage theory to simulate the nonlinear characteristics. This paper introduces the damage theory and damage elements, combined with commonly used components in series to simulate the whole process of rock creep property. Meanwhile by introducing elastopalstic damage components and Kelvin components model, a three-dimensional modified Kelvin creep damage model is established; and a rock equation of axial strain under triaxial compression is deduced; and fitting model parameters with creep experimental data of sandstone. The established model's parameters is less and easy to determine; and the derived three-dimensional model can better reflect the rock stress state in nature.

Keywordsaccelerated creep；damage theory；elastoplastic damage；axial strain