某矿山边坡单台阶三角体破坏分析

赵武鹍

(1.中钢集团马鞍山矿山研究院有限公司；2.金属矿山安全与健康国家重点实验室；3.华唯金属矿产资源高效循环利用国家工程研究中心有限公司)



某矿山边坡单台阶三角体破坏分析

赵武鹍1,2,3

(1.中钢集团马鞍山矿山研究院有限公司；2.金属矿山安全与健康国家重点实验室；3.华唯金属矿产资源高效循环利用国家工程研究中心有限公司)

摘要边坡岩体内存在着大量的软弱结构面，该类结构面往往演变为边坡滑坡的滑动面。以某矿山边坡台阶平面破坏为研究对象，应用能量系数、极限平衡理论、突变理论对该矿台阶边坡三角体的3种破坏状态进行了分析研究。结果表明：①对软弱带贯通的台阶边坡，将其视为刚塑性体更切合实际；②对软弱带不贯通的台阶边坡，其失稳防治的关键在于提高刚度比。

关键词台阶三角体能量系数极限平衡突变理论刚度比

矿山边坡是由复杂的地质岩体组成，其内往往存在与边坡尺寸数量级相当的软弱结构面，该类结构面的性状、空间分布特征及相互组合特征，往往控制着台阶边坡的稳定性，尤其在水、爆破振动的作用下易发展为边坡滑坡的滑动面。顺坡向结构面是产生台阶边坡破坏的主要因素，其倾角若小于边坡角，易产生平面滑动破坏，陡倾角易产生单台阶倾倒破坏，多组结构面相交易形成楔形破坏。对于台阶边坡破坏，费先科等[1]考虑了岩体中软弱夹层对滑动面的控制作用，提出了计算分析方法；谷飞宏[2]分析了岩质边坡的几何特征，总结出台阶宽度是边坡破坏规模的决定性因素，而最大宽度的坡脚则为最大的制约点，制约点决定破坏的边界条件；曹兴松等[3]在塑性极限分析的基础上，将能量系数作为台阶边坡稳定性的评价标准，并给出了计算公式；秦四清[4]对含软弱夹层的斜坡失稳进行了探讨，并建立了突变模型与混沌机制。对单台阶而言，破坏分为3种状态：①台阶受贯通性层面切割，形成的三角体完整性良好；②台阶受贯通层面切割后，由于受到其他节理裂隙影响，台阶坡脚出现直立面；③台阶受到非贯通性层面切割，使台阶受力体系呈现复杂状态，构成了非线性突变失稳现象。本研究根据某矿结构面特征及台阶结构参数，判断台阶破坏形式，分别应用极限平衡、上限定理、突变理论对台阶不同模式的平面破坏进行计算分析，并提出防护建议。

1边坡台阶三角体变形破坏力学分析

1.1贯通性层面切割的台阶三角体稳定性分析

本研究将边坡岩体设为刚塑性体，运用上限定理，以能量系数作为台阶边坡稳定性的评价标准进行分析，贯通性层面切割的台阶三角体的计算模型如图1所示。

图1　贯通性层面切割的台阶三角体分析模型

极限状态下滑体的内能耗散率Ds与实际作用的外力功率W的比值为能量系数，其计算公式为

(1)

式中,c为滑带的黏聚力，MPa；φ为滑面滑动方向与滑面的夹角，(°)；G为滑体重量，kN；β为滑面倾角，(°)；H为台阶高度，m；α为台阶坡面角，(°)。

当Es>1时，边坡处于稳定状态；Es<1，边坡失稳；Es=1，边坡处于临界状态。

1.2受层面切割并破坏坡脚的台阶三角体稳定性分析

设台阶坡脚受破坏超挖深度为h，边坡高度为H，坡顶面为水平状，因层面为贯通状，可不考虑地下水作用，假定软弱夹层以最不利的方式存在，即穿过开挖后坡脚，破坏模型如图2所示。

图2　受层面切割并破坏坡脚的台阶三角分析模型

安全系数计算公式为

(2)

式中，γ为岩体容重，kN/m3；h为超挖台阶坡脚垂高，m。

1.3非贯通性层面切割的台阶三角体稳定性分析

非贯通性层面切割的台阶三角体分析模型见图3，滑动面为非均匀软弱结构面。假定软弱夹层由2段不同力学性质的介质组成，一段具有应变弱化性质，一段具有弹性[4]。

图3　非贯通性层面切割的台阶三角体分析模型

当斜坡演化至临界状态时，稳定性系数计算公式为

(3)

式中，k为刚度比，为弹性性质区段介质的刚度与应变弱化区段刚度之比。

2工程应用

某矿露天采场下盘边坡长16km，存在1组追踪矿体倾向的层面，产状均值198°26′ ∠28°35′，该层面切割所有台阶，另外，下盘边坡的节理较发育，节理在小范围内将岩体切割成岩块，2组优势节理面(产状分别为0°～20°∠50°～70°，130°～150°∠80°～90°)的存在破坏了岩体的完整性，使得台阶失稳以平面破坏为主。已知：H=15m，γ=26.3kN/m3，β=28°35′，φ=24°，c=25.6kPa，h、α根据生产情况确定。

2.1贯通性层面切割的台阶三角体稳定性计算

据式(1)、式(2)，可计算出不同的台阶坡面角α对应的Es、Fs，结果见表1。由表1可绘制出α-Es、Fs关系曲线，见图4。

表1　不同台阶坡面角对应的台阶能量系数及安全系数

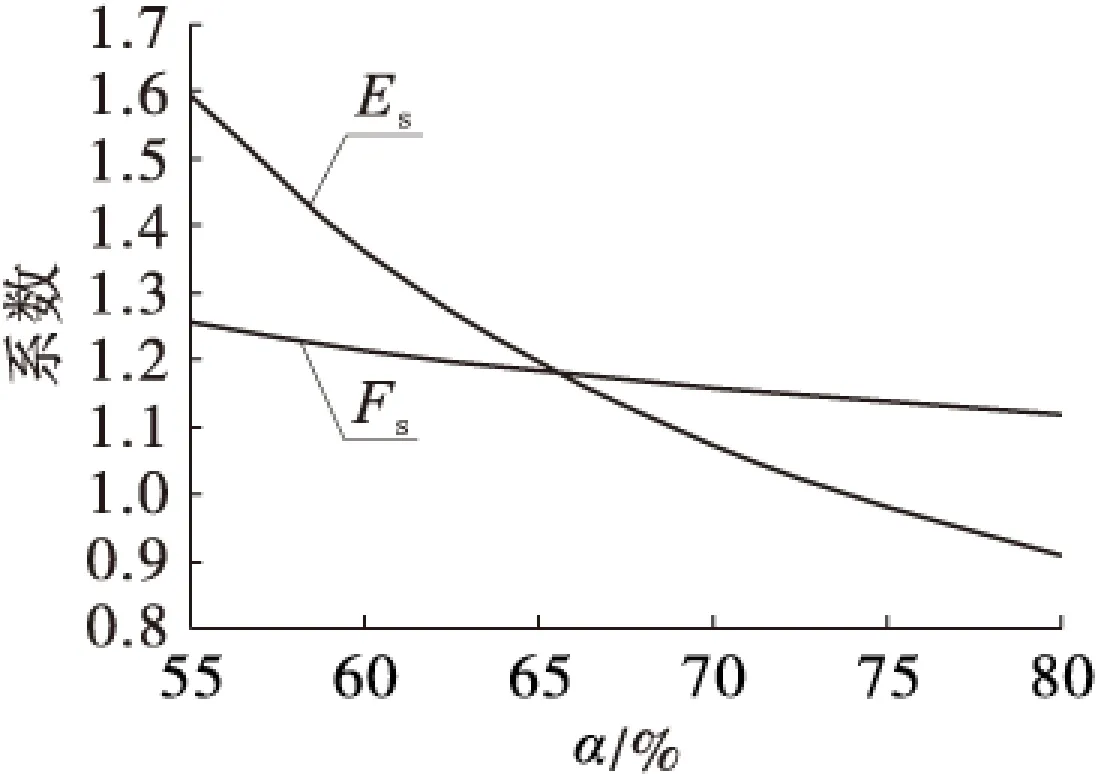
图4　α-Es、Fs关系曲线

由表1及图4可知：当台阶坡面角为80°、75°时，能量系数评价为台阶边坡不安全，极限平衡法为安全。在实际工程中，为了一定的安全储备，极限平衡法允许的安全系数为1.15，即可与能量系数法对应。极限平衡法评价的安全系数对台阶坡面角较不敏感，能量系数评价的安全系数则较敏感，更符合现场实际情况。

2.2受层面切割并破坏坡脚的台阶三角体稳定性

据式(2)，可计算多种情况下边坡台阶稳定系数，结果见表2。由表2可绘制出(α、h)-Fs关系曲线，见图5。

表2　与台阶坡面角及台阶破坏高度对应的台阶安全系数

图5　(α、h)-Fs关系曲线

由图5可知：当h一定时，Fs与α有关，α越大，台阶稳定状况越差；当台阶坡面角一定的前提下，随着h的增大，台阶稳定系数下降。

2.3非贯通性层面切割的台阶三角体稳定性分析

据式(3)计算出的台阶稳定系数见表3。由表3可知：随着k由小至大变化，Fk经历了由小至大的变化过程，可见，通过改变软弱夹层介质性质或弹性区段性质，可使得台阶不发生滑坡。

表3　台阶稳定系数计算结果

3结论

(1)与极限平衡法对比，对于含软弱带台阶边坡，以能量系数作为衡量边坡稳定的指标更切合实际。

(2)超挖台阶坡脚垂高及台阶坡面角越大，台阶边坡稳定性状态越差。台阶坡脚破坏区域应考虑支挡加固工程措施，采取合适的台阶坡面角，防止台阶大规模跨落。

(3)防止非均匀结构弱面切割台阶失稳的关键在于提高刚度比，即采取锚固、灌浆等工程措施，可改变潜在滑面的受力状态。

参考文献

[1]CHENZY,MorgensternNR.Extensionstothegeneralizedmethodofslicesforstabilityanalysis[J].JournalofCanadianGeotechnical,1983,20(1):104-119.

[2]谷飞宏.基于边坡特征的矿山台阶边坡破坏类型及规模分析[J].金属矿山，2014(7)：51-55.

[3]曹兴松，赵其华，周德培，等.机动位移法在顺层岩质边坡稳定性分析中的应用[J].山地学报，2009，23(2)：223-229.

[4]秦四清.斜坡失稳的突变模型与混沌机制[J].岩石力学与工程学报，2000，19(4)：486-492.

(收稿日期2016-04-11)

赵武鹍(1987—)，男，工程师，243000 安徽省马鞍山市经济技术开发区西塘路666号。