道床板长度对减振垫轨道结构振动性能影响分析

付琪璋

(中铁第一勘察设计院集团有限公司，西安　710043)



道床板长度对减振垫轨道结构振动性能影响分析

付琪璋

(中铁第一勘察设计院集团有限公司，西安710043)

摘要：橡胶减振垫整体道床是一种新型的减振轨道结构，然而，工程应用中，单元道床板结构长度的选择尚无明确指导性意见。采用模态分析、谐响应分析法分析不同道床板长度橡胶减振垫整体道床结构固有频率、振型及传递函数。分析表明：(1)单元道床板长度变化对道床垂弯、道床扭转振型主振频率影响较明显；(2)2.5、3.75 m单元道床轨道结构频谱幅值出现在一阶横弯振型频率，而≥5 m的道床板，其频谱幅值主要出现在道床沉浮振型对应频率附近；(3)减振垫整体道床频谱曲线幅值随着道床单元结构长度的增加而大幅减小；(4)当单元道床结构长度≥5 m时，频响幅值随单元长度变化不大。

关键词：轨道结构；道床板；振动；固有频率；传递函数

橡胶减振垫整体道床是一种新型的轨道减振结构，基于道垫物理特性可塑性好，该结构可适用于不同减振等级的结构设计之中，又由于其抗腐蚀性强、耐湿热性好、抗疲劳性能优越、造价适中、技术成熟、维护工作量小等特点而被国内外轨道交通领域大量选用。然而，工程应用中，单元道床板结构长度的选择尚无明确指导性意见。本文采用模态分析、谐响应分析法就不同道床板长度橡胶减振垫整体道床结构固有频率、阵型及传递函数等特性进行深入系统的研究，为橡胶减振垫整体道床单元结构合理长度设计提供依据。

1计算理论

1.1模态分析[1，2，6]

轨道结构与列车系统动力参数不匹配时，在一定行车速度条件下，车轮垂向激励会引起轨道结构与其共振，使得结构受力处于极其不利状态，从而诱发钢轨磨耗、扣件断裂、轨道结构开裂等病害，为避免共振发生，需对不同长度道床板固有频率及列车经过时激励频率进行分析比较。

模态分析是识别结构系统振动特性参数的重要手段，近些年来随着无砟轨道结构的发展，该手段被广泛应用于轨道交通领域。多自由度体系振动特性计算原理

式中[K]——结构刚度矩阵；

[M]——结构质量矩阵。

通过模态坐标代替物理坐标的手段实现微分方程解耦，进而求出系统各阶模态参数。

1.2谐响应分析[1，2，6]

在掌握系统固有频率的基础上，为进一步研究轨道结构各种频率传递特性，需对结构传递函数进行分析。

简谐激励的一般振动微分方程为

(1)

按微分方程理论，设特解形式为

X=Aeiωt

式中，A为待定常数。

代入式(1)可得

2模型及参数[7，8]

2.1计算模型

减振轨道系统结构自上而下依次为：钢轨、扣件、道床和减振垫组成，道床间设置伸缩缝，道床、减振垫间接触面位移协调一致，减振垫下为固定基础，力学模型如图1所示。

图1　减振轨道结构力学模型

模型中，将钢轨视为弹性点支承基础上的简支Bernoulli-Euler梁，分别考虑左、右股钢轨的垂向弯曲、横向弯曲及扭转自由度，钢轨支承点间隔为扣件间距，扣件考虑为垂向弹簧体系，道床、减振垫视为空间层状黏弹性体，减振垫下固定基础视为刚性支承。

本文基于ANSYS建立有限元模型，将钢轨简化为梁单元，单元节点具有x、y、z三向平动和转动自由度；扣件简化为弹簧阻尼单元，具有垂向变形能力；道床、减振垫采用实体单元，道床与减振垫间黏结，减振垫底部节点全约束。

2.2模型参数

本文模型计算参数选用：钢轨为60 kg/m；扣件支撑间距625 mm，节点静刚度30～40 kN/mm；道床板为C40钢筋混凝土结构，宽2.5 m、厚260 mm、单元道床板长度分别取为：2.5、3.75、5、7.5、10、12.5 m；道床垫参数见表1。

表1　橡胶道床垫参数

2.3边界条件

2.3.1模型长度

模型长度选取的合理与否之间会影响到计算结果，结合大量既有研究成果，取模型长度为65 m，可有效避免边界影响。

2.3.2约束条件

模型两端及减振垫底部均采用全约束方式。

3道床振动特性

基于减振轨道系统结构振动特性计算，专项提取不同长度单元道床结构振动特性分析如下。

3.1固有频率

结构模态是振动系统特性的一种表征，输出模态参数主要有固有频率、振型，可由此得到轨道系统在激振力作用下在哪些频率下会产生共振以及在各阶频率下的结构振型。

结构固有频率是表征其振动特性的重要指标，图2为轨道结构振动过程中道床表现出的基本振型。

表2列出不同长度单元轨道板振动固有频率及振型描述，图3表示单元道床板固有频率随板长变化关系。

分析表明：(1)单元道床板振动具有道床沉浮、道床侧滚、道床点头、道床垂弯、道床垂沉、道床扭转及道床横弯等主振型；(2)道床沉浮、道床侧滚、道床点头振型仅出现在20～30 Hz范围内，且受道床板长度因素影响较小；(3)一阶垂沉、一阶横弯振型分别会在105、160 Hz附近发生，受道床板长度因素影响较小；(4)道床垂弯、道床扭转振型受长度影响比较明显，覆盖250～110 Hz范围，且表现出随着道床板长度的增加，一阶振型发生所对应的频率越低；(5)道床板垂向振动主振频率为200～110 Hz，这与文献[9～11]研究成果一致。

图2　道床结构基本振型

道床板长度2.5m3.75m5.0m7.5m10.0m12.5m频率/Hz振型描述频率/Hz振型描述频率/Hz振型描述频率/Hz振型描述频率/Hz振型描述频率/Hz振型描述25.844道床沉浮24.955道床沉浮24.435道床沉浮23.904道床沉浮23.700道床沉浮23.620道床沉浮26.984道床侧滚26.101道床侧滚25.644道床侧滚25.176道床侧滚24.872道床点头24.327道床点头32.823道床点头29.193道床点头27.500道床点头25.790道床点头24.943道床侧滚24.802道床侧滚88.816一阶扭转61.300一阶垂弯41.965一阶垂弯30.597一阶垂弯27.423一阶垂弯26.006一阶垂弯105.077一阶垂弯61.825一阶扭转49.010一阶扭转37.459一阶扭转32.510一阶扭转29.309二阶垂弯108.243一阶垂沉105.573一阶垂沉85.46二阶垂弯45.553二阶垂弯33.716二阶垂弯29.938一阶扭转118.229二阶垂沉106.247二阶扭转88.584二阶扭转61.112二阶扭转47.780多阶垂弯36.526多阶垂弯122.618多阶垂沉109.388二阶垂沉105.236一阶垂沉75.103多阶垂弯48.189二阶扭转41.087二阶扭转123.987二阶扭转113.969多阶扭转108.542二阶垂沉88.380多阶扭转67.704多阶扭转49.237多阶垂弯146.068多阶扭转116.123三阶扭转109.691多阶扭转105.109一阶垂沉70.106多阶扭转55.548多阶扭转148.459多阶垂沉125.005多阶垂沉114.226多阶垂沉105.718二阶垂沉72.806多阶垂弯67.176多阶垂弯161.234一阶横弯143.555二阶垂弯123.206多阶扭转108.885多阶垂沉88.275多阶扭转71.778多阶扭转203.888多阶扭转158.165多阶垂弯130.887多阶垂沉109.792多阶垂弯105.074一阶垂沉88.646多阶垂弯219.189多阶扭转159.159一阶横弯149.169多阶垂沉109.829多阶扭转105.106多阶扭转89.182多阶垂弯237.151多阶垂沉195.061多阶垂沉152.270多阶扭转116.506多阶扭转105.432二阶垂沉102.39多阶扭转262.461多阶垂沉195.318多阶扭转158.378一阶横弯121.954多阶垂弯106.802多阶垂沉105.039一阶垂沉309.936多阶垂沉198.761二阶横弯165.492多阶扭转122.86多阶扭转109.101多阶垂沉105.261二阶垂沉334.922二阶垂弯266.587多阶垂沉181.493多阶扭转………………410.303多阶扭转267.049多阶扭转189.884多阶垂沉159.385一阶横弯159.633一阶横弯159.777一阶横弯430.272二阶横弯………………………………431.793二阶横弯430.413二阶横弯431.966二阶横弯431.539二阶横弯431.415二阶横弯………………………………

图3　道床板低阶振型随长度变化规律

3.2传递函数

在掌握轨道结构振动特性的基础上，取轴重170 kN激励荷载作用于轨道结构，得出不同长度轨道板频谱曲线如图4所示，同时提取各种板长响应幅值，绘制不同长度道床板频谱幅值曲线，如图5所示。

结合图4，并对照表2可知：(1)2.5、3.75 m单元道床轨道结构频谱幅值出现在一阶横弯阵型，且结构位移响应较大；(2)对于≥5 m的道床板，其频谱曲线幅值主要出现在沉浮振型对应频率附近；(3)5～10 m长度道床板频谱极大值会集中出现在100～125 Hz频率范围内，而12.5 m单元板频谱极大值出现在150～170 Hz频率范围。

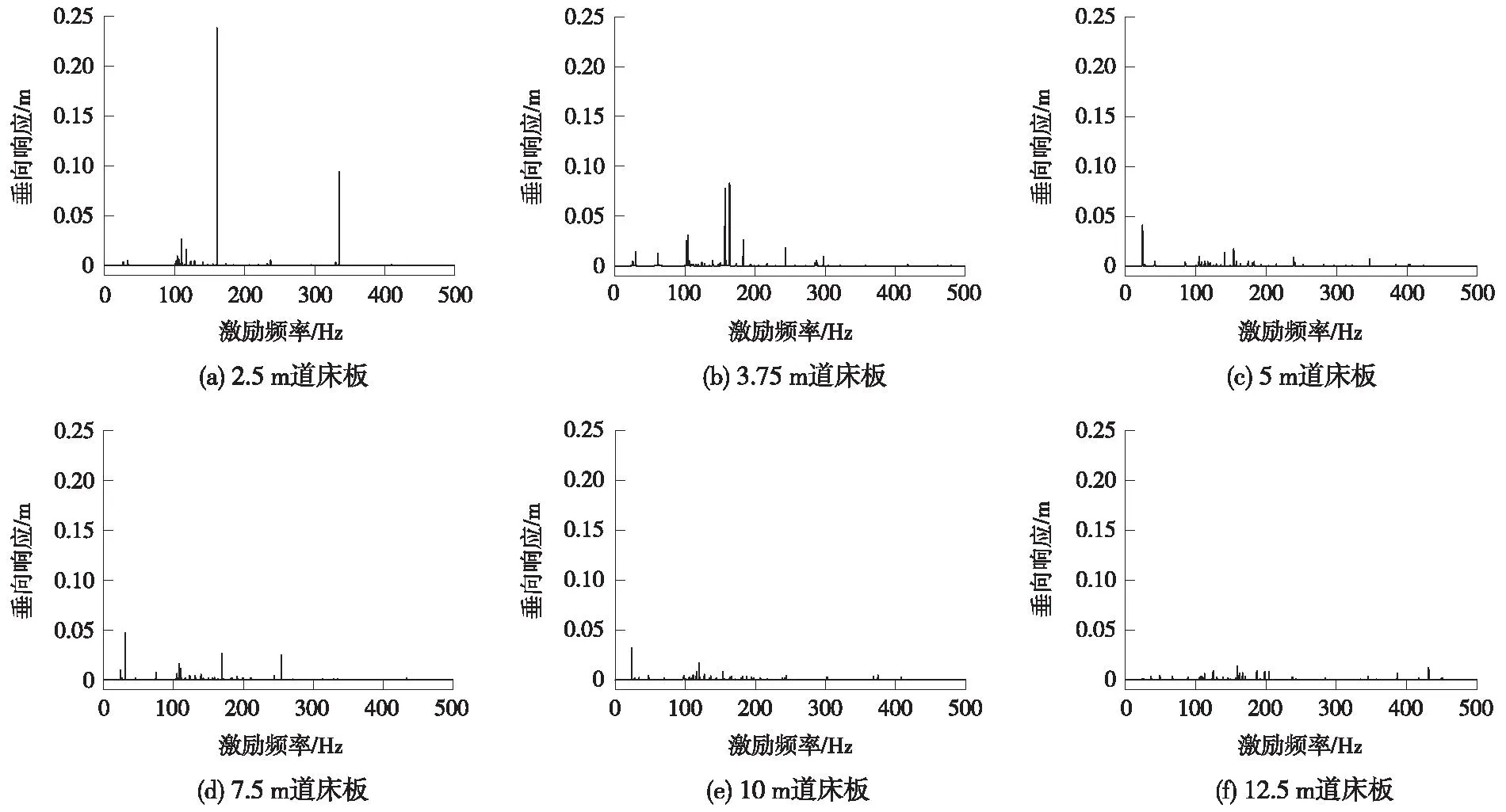
图4　不同长度道床板频谱曲线

图5　不同长度道床板频谱幅值分布

图5表明：(1)减振垫整体道床频谱曲线幅值随着道床单元结构长度的增加而大幅减小，12.5 m道床结构振动幅值仅为2.5 m的1/17；(2)当单元道床结构长度≥5 m时，频响幅值随单元长度变化影响不大。

4结论

针对新型橡胶减振垫整体道床轨道结构，从固有频率、阵型、传递函数等方面对该结构振动特性进行了深入研究，得出如下结论。

(1)单元道床板振动中道床沉浮、道床侧滚、道床点头、道床垂沉及道床横弯等振型主振频率，不随其长度变化而改变；道床垂弯、道床扭转振型主振频率受长度影响比较明显，且表现出随着道床板长度的越大，一阶振型发生所对应的的频率越低。

(2)道床垂向振动主振频率为20～110 Hz。

(3)2.5、3.75 m单元道床轨道结构频谱幅值出现在一阶横弯阵型，且结构位移响应较大；≥5 m的道床板，其频谱曲线幅值主要出现在沉浮振型对应频率附近，且结构位移响应不大。

(4)减振垫整体道床频谱曲线幅值随着道床单元结构长度的增加而大幅减小。

(5)当单元道床结构长度≥5 m时，频响幅值随单元长度变化不大。

参考文献：

[1]傅志芳.振动模态分析与参数辨别[M]. 北京：机械工业出版社，1990.

[2]曹树谦，张文德，萧龙翔.振动结构模态分析[M].天津：天津大学出版社，2001.

[3]翟婉明.车辆-轨道耦合动力学[M].第3版.北京：科学出版社，2007.

[4]刘学毅，王平.车辆-轨道-路基系统动力学[M].成都：西南交通大学出版社，2010.

[5]刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法[M].成都：西南交通大学出版社，2010.

[6]李成辉.轨道-车辆系统竖向振动模态分析[J].西南交通大学学报，1995，30(3):291-294.

[7]廖伯瑜，周新民，尹志宏.现代机械动力学及其工程应用[M]. 北京：机械工业出版社，2004.

[8]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007.

[9]陈果，翟婉明，左洪福.车辆—轨道耦合系统随机振动响应特性分析[J ].交通运输工程学报，2001，1(1):13-16.

[10]SHEN TON M J. The vibrational environment of the rail，sleeper and ballast[M]. TechnicalMemorandum. British Rail Research，Derby，1974.

[11]翟婉明.铁路轮轨冲击振动模拟与试验[J].计算力学学报，1999，16(1):93-99.

[12]温泽峰.钢轨波浪形磨损研究[D].成都：西南交通大学，2006.

[13]曹宇泽，田苗盛，杨其振.隔离式橡胶浮置板减振性能分析[J ].铁道工程学报，2013(2):34-38.

[14]李克飞，韩志伟，刘维宁，等.基于现场锤击试验的地铁轨道振动特性分析及参数研究[J].铁道标准设计，2014，58(2):12-16.

[15]刘克飞，刘学毅.橡胶浮置板轨道垂向动力特性分析[J].铁道建筑，2012(8):113-116.

收稿日期：2015-11-03； 修回日期：2015-12-02

作者简介：付琪璋(1985—)，男，工程师，2012年毕业于西南交通大学土木工程学院道路与铁道工程专业，E-mail：fuqizhang213@163.com。

文章编号：1004-2954(2016)06-0005-04

中图分类号：U213.2+12

文献标识码：A

DOI:10.13238/j.issn.1004-2954.2016.06.002

Analysis of Track Slab Length Impact on Vibration Performance of Damping Track Structure

FU Qi-zhang

(China Railway First Survey and Design Institute Group Co.，Ltd.，Xi’an 710043，China)

Abstract：The railway track with rubber vibration-damping pad is a new type of vibration damping track. However，the selection of the track slab length is not specified in engineering practices. Two methods of modal analysis and harmonic response analysis are applied to analyze the natural frequency，vibration mode and transfer functions of track slabs of different lengths. Research results show that: (1) the length of the unit slab has significant influences on the vibration frequency of vertical bending and torsion; (2) spectrum amplitude of unit slab appears in the transverse bending frequency of the first order at the lengths of 2.5，3.75m and when it is greater than or equal to 5m，it appears near the corresponding frequency of the floating vibration mode; (3) the spectrum amplitude of curves is greatly reduced with increase in length of the unit track slab; (4) the spectrum amplitude varies a little with the change of unit length where the length of the unit track structure is 5m or over．

Key words：Track structure; Track slab; Vibration; Natural frequency; Transfer function