高速铁路接触网风致振动与风偏的动态计算方法
韩佳栋
(中铁第一勘察设计院集团有限公司电化处,西安 710043)
高速铁路接触网风致振动与风偏的动态计算方法
韩佳栋
(中铁第一勘察设计院集团有限公司电化处,西安710043)
摘要:利用ANSYS软件建立接触网弹链、简链风致响应有限元模型,从导线弛度、张力及弹性角度,验证有限元模型的准确性;采用谐波合成法(WAWS)模拟针对接触网结构特点的脉动风场;计算系统在风荷载作用下的动态响应,利用空气动力学理论计算接触网平均位移,采用时程分析方法计算接触网动态位移,并将二者叠加得到接触网风致响应总位移。通过开展接触网气动弹性风洞试验,结果表明:提出的基于有限元的风致振动与风偏的动态计算方法与风洞试验结果基本吻合;该方法计算结果准确,具有较好的工程应用价值。
关键词:接触网; 风致响应; 风致振动; 风偏; 风洞试验;高速铁路
随着我国高速铁路的快速发展,列车运行的安全受到大风等恶劣气候、自然环境条件的影响程度愈加突出。根据国内外电气化铁路尤其高速铁路的运营情况,因风引起的弓网事故逐年增加。风区、风口的大风作用,隧道口的涡流风场作用或者隧道内上下行会车的列车风作用,会使接触网发生更大更复杂的振动及偏移,不仅影响接触网系统的疲劳寿命及弓网高速运行动态质量,甚至威胁弓网运行安全、引发弓网事故而导致铁路运营中断。因此,接触网系统在风载下的风致振动及风偏的准确计算具有重要的工程实际意义。
一般接触网设计中,风偏值采用均匀风速下静力学计算方法近似确定[1],近年来,对接触网风致振动影响的研究逐渐引起重视。国内外对于接触网风致振动主要进行了理论计算方面的研究[2-5],已见诸报道的接触网专业领域内的风洞试验主要涉及受电弓的气动力控制和挡风墙高度对接触线处横风的影响方面[6,7]。
本论文提出了一种接触网风致振动与风偏的动态计算方法,即建立接触网有限元模型,模拟针对接触网结构特点的风速时程,在该模型中施加风压作用,叠加均匀流场与紊流场下的风致响应位移,计算出接触网的竖向振动及风偏,并就风洞试验对该方法的理论计算结果进行了验证。
1接触网风致响应有限元模型
通过承力索弛度曲线非线性分析、定位器受力分析及约束施加,确定承力索曲线,建立基于ANSYS的接触网风致响应有限元模型。
1.1接触网基本参数
弹链、简链结构高度分别为1.6、1.1 m,吊弦布置分别为(5+8×5+5)、(2.5+5×9+2.5) m,跨距50 m,4跨,拉出值250 mm,其他参数见表1。
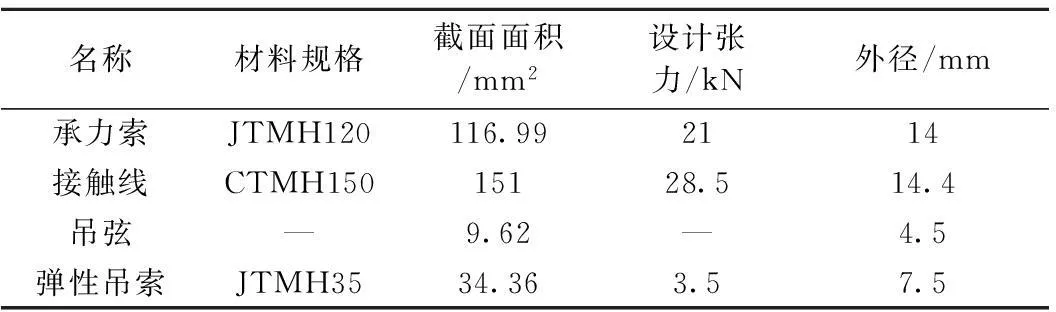
表1 接触网系统基本参数
1.2承力索弛度曲线非线性分析
承力索弛度曲线的非线性分析是风致响应模型建立的关键,过程为:(1)视承力索、接触线张力不变,建立接触网三维有限元模型;(2)使支柱和腕臂结构刚性化,先后进行承力索在本身自重作用下、在承力索、接触线、吊弦和定位器重力作用下的几何非线性分析,积累重力刚度;(3)恢复支柱和腕臂结构的弹性,进行悬挂系统与支撑系统的耦合分析,最终完成悬挂系统的找形工作。其中找形是否满足要求通过判断模型导线的张力、弛度来确定。选取link10单元模拟接触线、承力索,采用BEAM44单元模拟支柱、腕臂、腕臂支撑、定位管、定位器及定位器支座,建立由悬挂系统、腕臂结构、定位装置及支柱组成的有限元模型。
1.3定位器受力分析及约束施加
定位器受力分析见图1,力矩平衡方程见式(1)。
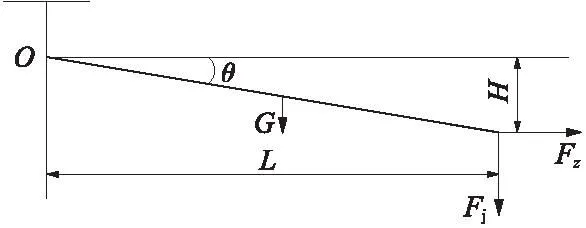
图1 定位器受力分析
(1)
式中,Fz为接触线之字力;Fj为定位点处接触线对定位器的竖向拉力;G为定位器自重。
Fz、Fj、L分别采用式(2)、式(3)、式(4)计算
(2)
式中,a为拉出值;L1、L2分别为左、右跨距值;F为接触线张力。
(3)
式中,gj为接触线单位长度自重;ld1为第一吊弦长度。
(4)
式中,l为定位器长度。
按式(1)施加荷载,由式(1)、式(2)、式(3)及式(4)可得出定位器角度θ;定位器可绕O点在腕臂结构平面内及水平面内旋转,按此施加约束,即可确定定位器状态。
1.4风致响应有限元模型及其误差分析
接触网弹链、简链风致响应有限元模型分别见图2、图3。
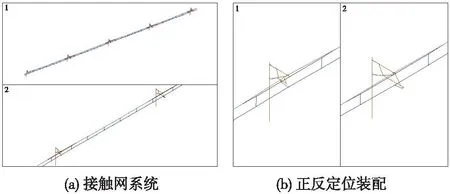
图2 弹链风致响应有限元模型
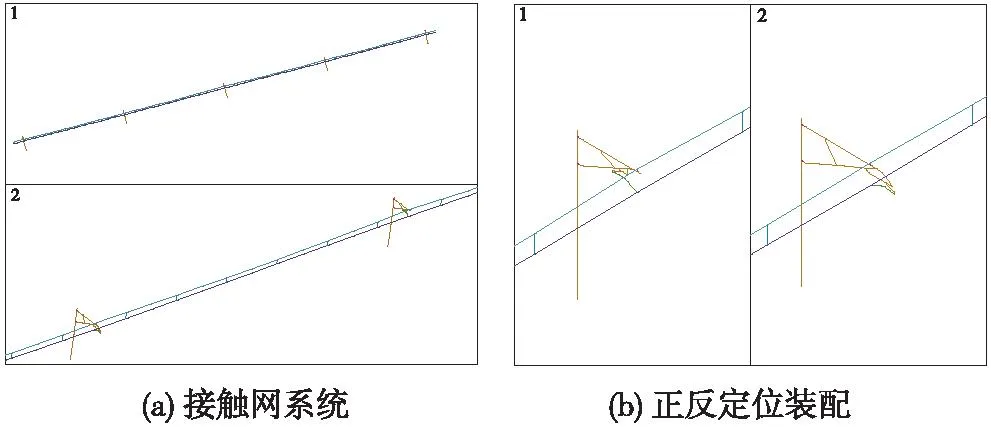
图3 简链风致响应有限元模型
1.4.1导线弛度及张力误差
表2、表3分别所示为弹链、简链悬挂系统有限元模型导线弛度及张力的模型计算值与理论目标值(设计参数或常规算法计算值)的比较情况。经对比,模型计算值与理论目标值差别较小,误差小于3%。

表2 弹链模型计算值与理论目标值对比结果
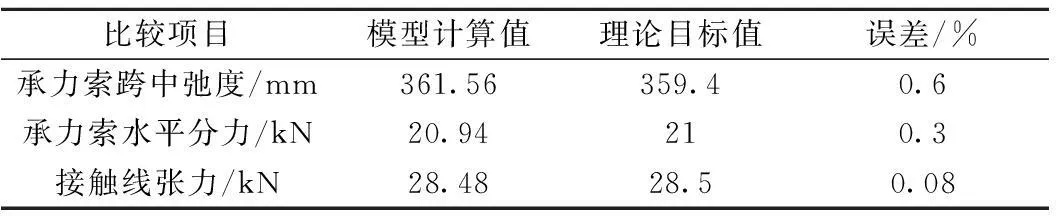
表3 简链模型计算值与理论目标值对比结果
注:1.常温;2.不考虑因温度变化形成的张力增量;3.不考虑冰负载、风负载的影响。
1.4.2弹性误差分析
图4(a)、图4(b)分别所示为弹链、简链悬挂系统模型一跨内的弹性变化曲线,表4所示为模型弹性计算值与经验公式[8]计算值的对比。
如图4所示,弹链弹性均匀度优于简链,且一跨内弹性变化曲线与国内同行ANSYS计算结果相符[9,10];见表4,模型弹性计算值较经验公式计算值稍大,其中弹链偏差较小(小于4%),而简链偏差较大(约10%)。
综合从导线弛度及张力、弹性角度对有限元模型的检验看,采用该风致响应模型进行风致振动及风偏动态计算是可行的,且由于模型弹性值较经验公式计算值大,风致响应计算结果较为保守。
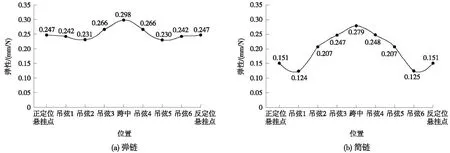
图4 弹链、简链一跨内弹性变化曲线

项目经验公式经验公式计算值/(mm/N)模型计算值/(mm/N)误差/%弹链跨中弹性ηmax=l/[3.5·(Tj+Tc)]0.2890.2983.1简链跨中弹性ηmax=l/[4·(Tj+Tc)]0.2530.2799.4
2接触网风场
2.1平均风的计算
风一般可以分为平均风和脉动风两部分,假设作用于结构上坐标为(x,y,z)的点的风速为
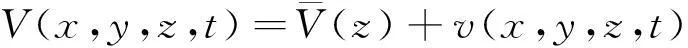
(5)
式中,右边相加的两部分分别为距地面高度z处的平均风速和对应的脉动风速[11~13]。
在空间上,平均风速会随着高度的变化而变化,其描述主要有对数律和指数律。本文选取指数率[14,15]计算平均风速,具体公式如下
(6)
式中,v10为距离地面10 m高度处的环境风速,标准参考高度取10 m;H为当前高度;α为地表粗糙度指数,本模型取0.16;K为挡风屏后接触线、承力索高度处的风速系数,这里按桥梁4 m挡风屏风场风洞试验结果取值,即接触线处风速系数0.76,承力索处风速系数1.21[22]。
2.2脉动风的模拟
2.2.1采用的功率谱
脉动风速既是时间的函数,又随空间位置(x,y,z)而异,假设风场是空间各点处随机风波的总和,那么该随机场可以处理为多变量一维(nV-1D)随机过程。谐波合成法(WAWS)是模拟多变量随机过程的主要方法之一。针对接触网的结构特点,将脉动风假定为具有零均值的平稳高斯随机过程,利用Deodatis谐波合成法模拟脉动风速时程样本。
为计算接触网水平方向的风偏和竖直方向的振动位移,分别选用经Simiu修正的Kaimal谱式(7)和Lumley-Panosfsky谱式(8)模拟接触网的水平脉动风速时程和竖向脉动风速时程[16,17]
(7)
(8)
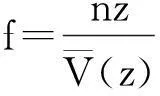
空间任意两点脉动风速互谱的相干函数[18]如下
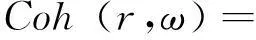
(9)
计算水平向脉动风速互谱的相干函数时Cz和Cy分别取为10和16;计算竖向脉动风速互谱的相干函数时Cz和Cy分别取为7和8。
2.2.2模拟的风速时程
针对兰新铁路第二双线百里风区地理环境及接触网结构特点,按上述方法及风谱,模拟出了接触网的水平风速时程和竖向风速时程,见图5。其中模拟计算的主要参数:截止频率4π、频率分段数1 024、样本时间间隔0.25 s、地面粗糙度0.05。
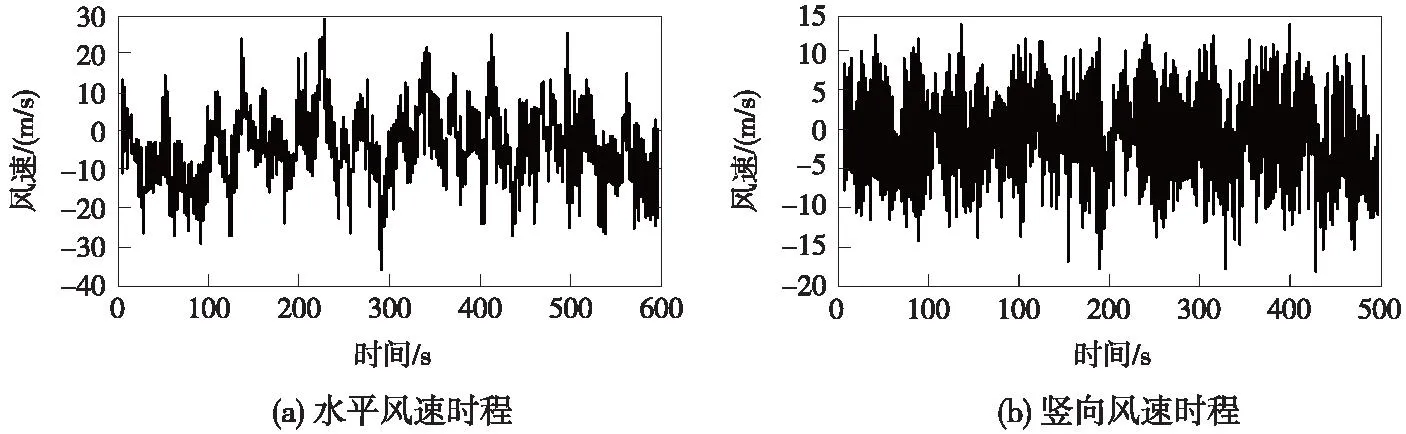
图5 简链第三跨定位点处的风速时程
对模拟得到的风速时程进行统计分析,得到了模拟点风速时程的均值和均方根(以简链第三跨定位点为例)与目标谱对应的值进行对比,如表5所示。从表可以看出,模拟风速的均值、均方根与目标风速相差均较小。
图6所示为模拟的风速时程的功率谱与目标谱的比较,模拟水平功率谱及低频段的竖向功率谱与目标谱无论极值还是趋势都吻合很好,竖向功率谱在高频段虽然有一定的波动,但整体趋势较为吻合。

表5 风速统计数据模拟值与目标值对比结果
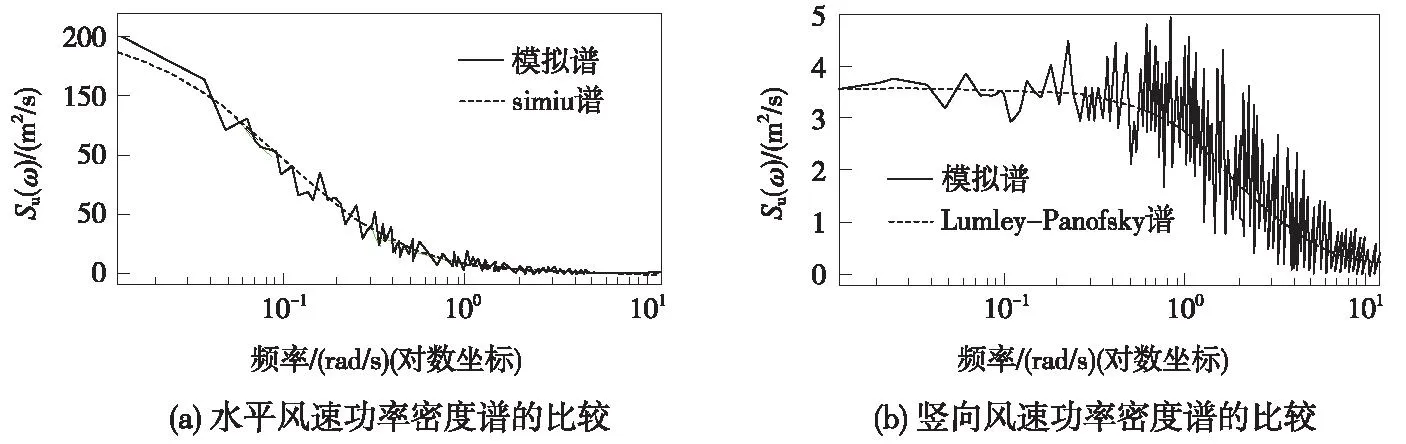
图6 模拟的风速功率谱与目标谱的比较
3接触网风致振动与风偏计算
在接触网有限元模型中施加风压作用,利用空气动力学理论[19]计算接触网平均位移,采用时程分析方法[20,21]计算接触网抖振位移;叠加竖向平均位移与竖向抖振位移获得接触网在风压作用下的风致振动总位移,叠加水平平均位移与水平抖振位移获得接触网在风压作用下的总风偏。
水平方向单位长度接触线、承力索的阻力
(10)
竖直方向单位长度接触线、承力索的升力
(11)
单位长度接触线、承力索的力矩
(12)
由于接触线的横截面形状为带有沟槽的铜合金圆形导线,非普通规则圆形形状,需通过接触线静力节段模型风洞试验测试接触线阻力系数,为接触网风致响应研究提供参数。按接触线静力节段模型风洞试验结果,接触线阻力系数取值0.77。
弹链、简链接触线正定位、反定位、跨中风致振动总位移及跨中总风偏的计算结果见表6。
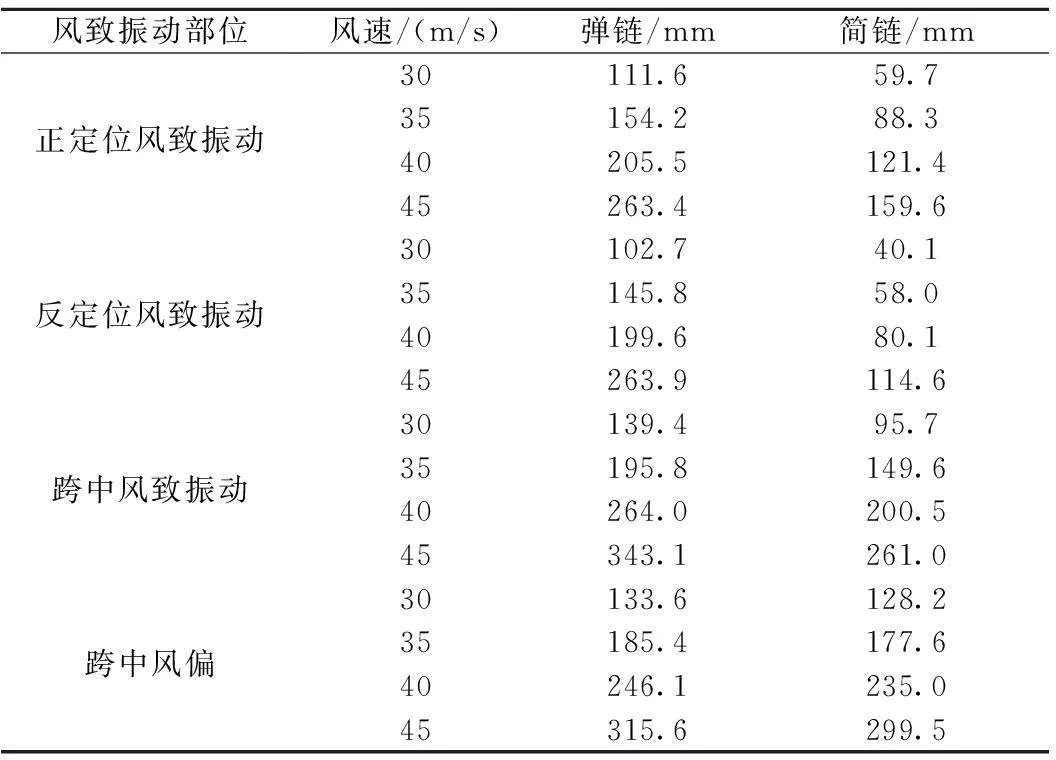
表6 接触网风致振动总位移及跨中总风偏
4气动弹性风洞试验及其结果分析
为了验证理论计算结果,更准确地模拟接触网结构动力特性,评估接触网系统风致响应,采用接触网风致响应气动弹性风洞试验进行验证。风洞试验采用3跨简链接触网缩尺模型,几何缩尺比1/7.5,见图7。

图7 接触网气动弹性风洞试验模型
经振型、频率及跨中弹性测试,接触网系统有限元模型计算与风洞试验振型一致、频率误差小于5%(对比结果见表7),弹性误差小于6%;经对比,接触网风致振动与风偏的有限元计算结果与风洞试验结果基本吻合,图8所示为跨中竖向位移的对比结果。
接触网气动弹性风洞试验结果表明,该接触网风致振动与风偏的动态计算方法可行、计算结果较为准确。
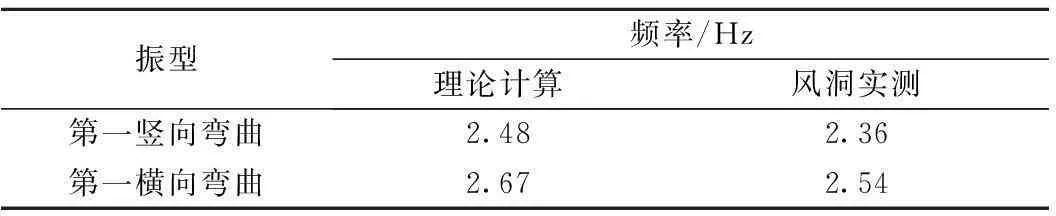
表7 振型、频率理论计算与风洞实测对比结果
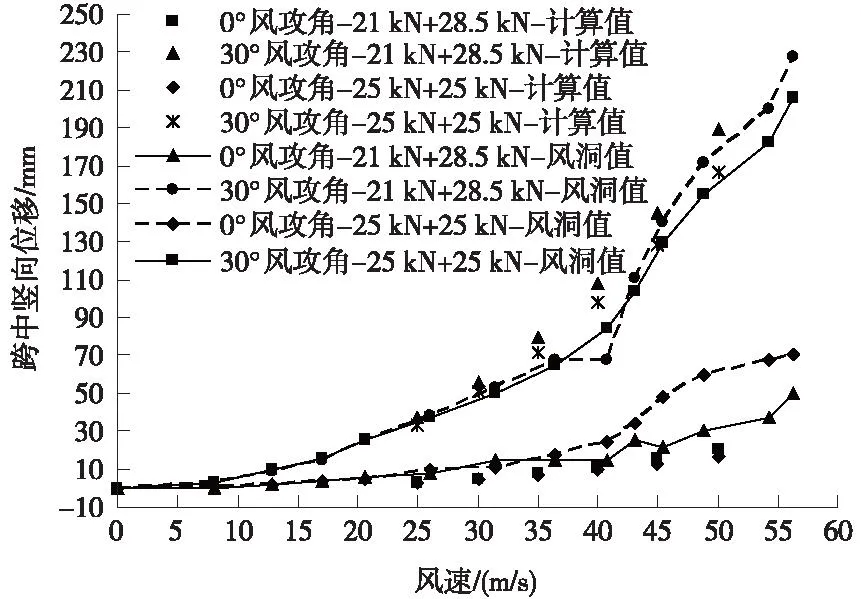
图8 风洞试验与理论计算对比结果
5结论
提出了基于有限元风致响应计算风致振动位移与采用时程分析计算抖振位移的方法,将振动位移与抖振位移进行叠加,以获得接触网大风环境下的实时运动状态,以兰新铁路第二双线桥梁4 m挡风屏区段为研究对象,采用该方法计算得到了接触网正定位、反定位及跨中的风致振动位移及跨中风偏,并通过风洞试验对计算结果进行了有效验证。
经导线弛度及张力的误差分析,接触网风致响应模型计算值与理论目标值误差小于3%;经弹性误差分析,模型弹性较经验公式计算值稍大,风致响应计算结果趋于保守。经接触网气动弹性风洞试验验证,风洞试验与接触网系统有限元模型计算振型一致、频率误差小于5%、弹性误差小于6%,且接触网风致振动与风偏的有限元计算结果与风洞试验结果基本吻合。
本研究提出的方法可行、计算结果准确,对于接触网风致响应的计算及分析具有较好的工程应用价值。
参考文献:
[1]于万聚.高速电气化铁路接触网[M].成都:西南交通大学出版社,2009.
[2]朱伟林,周全,罗伟.基于模拟脉动风场的铁路接触网风振响应分析[J].机械与电子,2011(12):76-78.
[3]韩佳栋,曹树森,刘晓红,等.强风地区接触网风振响应分析[J].铁道建筑技术,2010(S):207-210.
[4]谢将剑,王毅,苑玉超,等.基于DIT-FFT优化WAWS法的接触网风致响应分析[J].空间结构,2013,19(2):63-69.
[5]曹树森,柯坚,邓斌,等.强风地区接触网动力稳定性分析[J].中国铁道科学,2010,31(4):79-84.
[6]A. Collina,A. Facchinetti,F. Resta. A feasibility study of an aerodynamic control for a high speed pantograph[C]∥IEEE /ASME international conference on advanced intelligent mechatronics,2007:1-6.
[7]Sergio Avila-Sanchez,Oscar Lopez-Garcia,Jose Meseguer. Influence of Embankments with Parapets on the Cross-Wind Turbulence Intensity at the Contact wire of Railway Overheads[C]∥Proceedings of the 2010 Joint Rail Conference. Urbana: American Society of Mechanical Engineers,2010:1-8.
[8]中铁电气化局集团有限公司译.电气化铁道接触网[M].北京:中国电力出版社,2004.
[9]郝方涛,吴积钦.基于ANSYS的接触网弹性计算[J].电气化铁道,2004(3):31-33.
[10]李瑞平,周宁,梅桂明,等.初始平衡状态的接触网有限元模型[J].西南交通大学报,2009,44(5):732-737.
[11]王之宏.风荷载的模拟研究[J].建筑结构学报,1994,15(1):44-52.
[12]张相庭.结构风压和风振计算[M].上海:同济大学出版社,1985.
[13]黄本才.结构抗风分析原理及应用[M].上海:同济大学出版社,2001.
[14]中华人民共和国铁道部.TB 10009—2005铁路电力牵引供电设计规范[S].北京:中国铁道出版社,2005.
[15]中华人民共和国交通部.JTG/T D60—01—2004公路桥梁抗风设计规范[S].北京:人民交通出版社,2004.
[16]Panofsky H A,Mccormick R A. The spectrum of vertical velocity near the surface[J]. Quarterly Journal of the Royal Meteorological Society,1960(86):495-503.
[17]Lumley J L,Panofsk H A. The structure of atmospheric turbulence[M]. New York: Wiley,1964.
[18]丁泉顺,陈艾荣,项海帆.大跨度桥梁空间脉动风场的计算机模拟[J].力学季刊,2006,27(2):184-189.
[19]Simiu E,Scanlan R H.风对结构的作用——风工程导论[M].刘尚培,项海帆,谢雾明,译.上海:同济大学出版社,1992.
[20]Davenport A G. The Application of Statistical Concepts to the wind Loading of Structures[J]. Ice Proceedings,1961,19(4):449-472.
[21]胡晓伦.大跨度斜拉桥颤抖振响应及静风稳定性分析[D]. 上海:同济大学,2006.
[22]刘改红.风区挡风墙/屏影响下接触网设计风速计算研究[J].铁道标准设计,2013(9):90-93.
收稿日期:2015-11-23; 修回日期:2015-12-09
基金项目:铁道部科技研究开发计划(2010G019-G)
作者简介:韩佳栋(1975—),男,高级工程师,工学学士,E-mail:878955573@qq.com。
文章编号:1004-2954(2016)06-0121-05
中图分类号:U238; U225
文献标识码:A
DOI:10.13238/j.issn.1004-2954.2016.06.025
Dynamic Calculation of Wind-induced Vibration and Deviation of High-speed Railway OCS
HAN Jia-dong
(Electrification Design Department,China Railway First Survey and Design Institute Group Co.,Ltd.,Xi’an 710043,China)
Abstract:Based on the finite element model of wind-induced response established with ANSYS software for catenery of elastic and simple types,the accuracy of the finite element model is validated through the comparison between theoretical values and the calculated values of the model in terms of tension and sag,stress and elasticity of the contact wire. Weighted amplitude wave superposition (WAWS) method is used so simulate fluctuating wind field according to the characteristics of catenary structure. Furthermore,dynamic displacement response simulation under the simulated wind load is calculated. The average displacement of OCS is calculated based on air dynamic theory,and the dynamic displacement of OCS is calculated by using time history analysis. And the combination of the two displacements results in the total wind-induced displacement of OCS. The wind tunnel test results of aeroelasticity show that the result of wind-induced vibration and deviation basically matches that of wind tunnel. This method is proved accurate and applicable.
Key words:Overhead line systems (OCS); Wind-induced response; Wind-induced vibration; Wind tunnel test; High-speed railway

