基于单向点格自动机的UPG文法识别并行算法

李玉萍

（商丘师范学院 计算机与信息技术学院，河南 商丘 476000）

基于单向点格自动机的UPG文法识别并行算法

李玉萍

（商丘师范学院 计算机与信息技术学院，河南 商丘 476000）

UPG文法是一种特殊的生成文法，在分析的过程中可以没有回溯。该文法能够更好地描述自然语言中特殊的语法结构。单向点格自动机是进行语言并行识别的模型。通过对该文法和点格自动机深入的分析，提出了一种在并行环境下基于点格自动机的无回溯的语法分析和识别算法。文章通过实例详细描述了算法并行处理的过程，验证算法的正确性和可行性。

UPD文法；单向点格自动机；语法分析

点格自动机是一种数学模型，由J.von Neumann在40年代提出，最初用它来模拟生物系统中某些自组织现象。随着计算机技术的发展，它已成为分析复杂现象的一种有效工具。

目前，大多数程序设计语言采用上下文无关文法进行描述，但上下无关文法描述问题的能力有限，因此对上下文无关文法进行扩充，形成了一种特殊的UPG文法。UPG文法作为一种特殊的生成文法，具有重要特性，在进行语法分析的时可以没有回溯，能够更好地描述自然语言中特定的语法结构。

随着计算机的发展趋向于并行化，多处理机并行处理是不可逆转的时代，因此对UPD文法在并行环境下处理过程的分析和研究有其理论和实践意义。根据点格自动机和UPD文法的特殊的属性，文章提出了利用单向点格自动机模型对UPD文法进行并行转换和并行语言识别的算法，通过实例进行分析，说明了算法的正确性和可行性。

1 基本概念

定义1UPG文法是一个五元组 G=(N,T,P,S,$)，N是一个非空的非终结符的有穷字母集；T是一个非空的终结符的有穷字母集，T和N的交集为空；S为开始符号，$是一个特殊的结束符号，$既不属于终结符集合也不属于非终结符集合，P是语法规则的有限集合，该规则形式如：

α→β,α→$β,α$→β$,$α$→$β$或者$A$→$$

其中α,β∈(N⋃T)+,A∈N，α至少包含一个非终结符，$A$→$$为一个空规则，这些规则必学满足下列条件

（1）每一个规则右边不能出现S,$S,S$,$S$

（b）如果 β1=γβ2γ',其中γ，γ'∈（N⋃T⋃$）+，则R1=R2

定义2对于一个UPG文法，如果α→β,η=γαδ,可以得到 ξ=γβδ，则称 ξ是η的直接推导，即η⇒ξ。定义⇒*为传递闭包，经过n步推导可表示为η⇒nξ。如果 $S$⇒*η，则称η为一个句型，该文法的语言可以定义为 L(G)={ω∈T*|$S$⇒*$ω$}。

定义3对于一个UPG文法，η=γβδ，其中γ，δ∈（N⋃T⋃$）*，|γ|=j-1（表示γ的长度），如果α→β，ξ=γαδ，则对任意的[α→β,j]为η的反向有效项目，对ξ可以直接规约为 η[α→β,j]ξ，因此⇐*，⇐的定义和⇒*，⇒的定义类似。

定理1G=(N,T,P,S,$)是一个UPG文法，对于串η，如果η⇐n$S$，其中η∈（N⋃T⋃$）+，η⇐ξ，则η⇐ξ⇐n-1$S$。

定义4假设l，r为非负整数，α=γα'δ,β→γβ'δ,|γ|=l,|δ|=r，则R=[α→β,(l,r)]为上下文索引规则，γ、δ为左右上下文，（l，r）为上下文索引。

定义5对于一个UPG文法，根据定义4可以该文法的规则集P可以被改写为 [α→β,(l,r)]，[α$→β$,(l,r)]，[$α→$β,(l,r)]，或者 [$A$→$$,(1,1)]，其中α∈((N⋃T)+-T+)，β∈(N⋃T)+，α≠β,A∈N

定义6G=(N,T,P,S,$)是一个UPG文法，ξ∈（N⋃T⋃$）+，{I 1…Ik}为ξ所有的反向有效项目集，Ii=[αi→βi,(li,ri)]叫直接最大并行约简，则

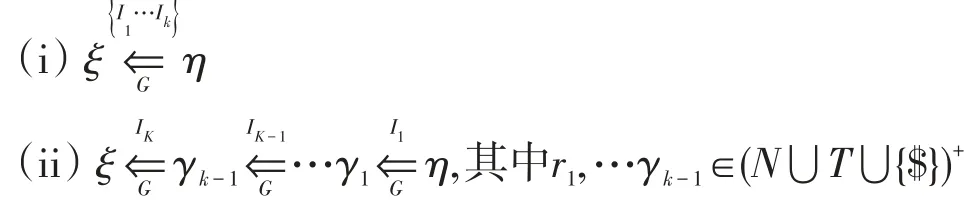
定理2UPG文法，如果 ξ⇐m$S$，对于定义5的任意的反向有效项目集则有

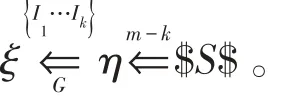
定义7一个单向点格自动机（OCA）是一个五元组C=(Q,Q0,Qf,#,fC)，这里Q是非空的有限状态集，Q0是一个非空输入状态集合，Qf为接收状态（Q0⊆Q,Qf⊆Q），fC为（(Q⋃{#})2→Q）的局部转换函数，该函数满足：f（Ca,b）=#，当且仅当b=#。

全局变量 F(a1a2…an)=fC(#,a1)fC(a1,a2)…fC(an-1,an)

当n=1,F(a1)=fC(#,a1)。

定理3令L⊆Q+0为单向点格自动机可以实时识别的语言，则存在一个具有反向有效项目集的UPG文法G，使得L(G)=L。对于每一个字符串ω∈L可以通过反向有效项目集约简得到。

定理4令L可以被OCA所识别，则一定存在一个UPG文法，使得L(G)=L。

2 基于单向点格自动机的UPG文法并行识别算法

2.1 利用点格自动机并行构造U?PG文法的反向有效项目集算法

算法1：给定 C=(Q,Q0,Qf,#,fC)为点格自动机，Q=(a1a2…am)；UPG文法 G=(N,T,P,S,$)，这里N={S,S',S"}⋃{A1,…Am}⋃{*}。根据点格自动机对文法G的反向有效项目集的并行构造如下：

（a）对于每一个状态ai∈Qf，则对应的反向项目集为[S→S'AiS",(0,0)]；

（b）对于ai,aj,ah∈Q,fC(ai,aj)=ah，则对应的反向项目集为[Ah*Ah→AiAj*,(0,0)]；

（c）对于ai,aj,ah∈Q,fC(#,ai)=aj，则对应的项目集为[$S'Aj→$Ai*,(1,0)],[S'→S'Ah*(1,0)]；

（d）对于ai∈Q-Qf,则对应的项目集为[S"$→Ai$,(0,1)],[S"→AiS",(0,1)]；

（e）对于每一个状态ai∈Q0,，则对应的项目集为[Ai*Aj→ai,(0,0)]；

2.2 UPG文法的并行识别算法

算法2：输入字符串$b1b2…bn$

输出：如果b1b2…bn是L（G）中某个长度为n的句子，那么返回真；否则返回假。

（i）对于输入串中每个字符b1，b2，…，bn利用算法1（e）中的最大反向规约项目集并行规约；（ii）对于由（i）得到的字符串利用算法1（b）中的最大反向规约项目集并行规约；

（iii）对于由（ii）得到的字符串利用算法1中的（c），（d）中的最大反向规约项目集并行规约；

（iv）经过n+2步得到的字符串S'AiS"利用算法1中的（a）中的最大反向规约项目集进行规约，得到字符串$S$，

从而可以得出$b1b2…bn$⇐n+2$S$，则该字符串可以被文法UPG文法识别。

3 实例分析

假设L={a2k|k=1，2，…}，L可以被点格自动机（OCA）所识别，点格自动机OCA C=({a,b,c},{a},{c},#,fC)，fC的定义如下：

fC（b,a）=c，fC（c,a）=c，fC（a,a）=a，fC（c,b）=b，fC（b,c）=c，fC（#,a）=b，fC（#,b）=b。

根据算法1，并行构UPG G=({A,B,C,S,S',S",*},a,P,S,$)的反向有效项目集，可得

[S→S'CS",(0,0)]，[C*C→BA*,(0,0)]，[B*B→CA*,(0,0)]

[A*A→AA*,(0,0)]，[B*B→CB*,(0,0)][C*C→BC*,(0,0)]

[$S'B→$A*,(1,0)]，[S'→S'A*,(1,0)]

[$S'B→$B*,(1,0)][S'→S'B*,(1,0)]

[S'→S'C*,(1,0)]，[S''$→B$,(0,1)]

[S''$→A$,(0,1)]，[S''→AS'',(0,1)]

[S''→BS'',(0,1)][A*A→a,(0,0)]

给定输入字符串为$aaaa$

根据算法2对输入字符串分步并行规约可得

则字符串aaaa可以被该文法识别。

4 结束语

UPG文法是一种特殊的文法，可以利用单向点格自动机构造并行UPD文法的反向有效项目集。对于给定字符串的语法识别的过程中，根据UPD文法并行分析算法，对字符串找最大规约项，如果可以规约到开始符号，则该字符串符合该文法。但算法的性能以及处理器内部通信，负载分布等问题还需要进一步的研究。?

参考文献：

［1］J.Lee，K.Morita.Uniquely parallelparsableunification grammars［J］.Leice Transaction on Information and Systems，2001，84（1）：21-27.［2］罗莎.一种高效的自然语言理解语法分析算法［J］.科技通报，2013，（12）：91-93.

［3］W.Bucher，K.Culik II.On real timeand linear time cellularautomata［J］.Iform.Theory，1995：307-325.

［4］Gibbons A，RytterW.Efficientparallelparsingalgorithms［M］.Cambridge University Press，1990.

［5］周勇.基于并行计算的数据流处理方法研究［D］.大连理工大学，2013.

［6］陈国良.并行计算.北京：高等教育出版社［M］，2011.

［7］段晓东.元胞自动机理论研究及其仿真应用［M］.北京：科学出版社，2012.

Parallel Processing of Syntax Parsing Algorithm for UPD Grammar Based on One-way Cell Automata

LIYu-ping
（DepartmentofComputerand Information Technology,Shangqiu Normal College, Shangqiu,Henan,476000,China）

A uniquely parsable grammar（UPD）is a special kind ofgenerative grammarwhere parsing can be performed withoutbacktracking.UPD grammars have greater generative power than the context-free grammars.This family ofgrammarsand one-way cellautomata is deeply analyzed.A recognition and parsing algorithm under Parallelenvironment ispresented.The processofparallelprocessing is described by instance and the validity of the algorithm is verified.

UPD grammars;One-way cellautomata;Syntax Analysis

TP301

A

1008-9659（2016）02-0071-04

2016-03-25

河南省科技厅基础与前沿技术研究计划项目（142300410395）。

李玉萍（1982-），女，河南开封人，讲师，硕士，主要从事并行编译技术研究。