电磁感应透明介质中矢量Thirring模型的实现
张 昆, 李慧军
(浙江师范大学 物理系,浙江 金华 321004)
电磁感应透明介质中矢量Thirring模型的实现
张 昆, 李慧军*
(浙江师范大学 物理系,浙江 金华 321004)
借助电磁感应透明效应,提出在单组分六能级原子介质中实现Thirring模型的方案。从光与原子相互作用的麦克斯韦—薛定谔方程组出发,推得探测场两个偏振分量满足的耦合非线性薛定谔方程,通过控制可调物理参数,实现了(1+1)维的Thirring模型。在此基础上,研究该模型中存在的基孤子,并探讨了该孤子的稳定性。与以前的研究相比,不仅更容易实现的单组分原子、两束激光场,而且该体系还可用来讨论暗暗孤子对。
Thirring模型;电磁感应透明;多重尺度;交叉相位调制;孤子
自激光问世以来[1],非线性光学的研究引起了人们的极大关注,并迅速成为一门新兴学科[2]。由于共振介质对光场的强烈吸收,非线性光学效应只能通过强光与非共振介质相互作用来实现,且所实现的非线性效应较弱。
直到20世纪90年代,电磁感应透明(EIT)效应[3]为共振介质中研究弱光非线性光学打开一个突破口。EIT利用外加控制场所诱导的量子干涉效应消除了共振介质对探测场的吸收。该体系具有许多新颖的特性,包括:对入射场无吸收[4];极大减慢光场的群速度[5];具有确定能级,可方便地利用电磁效应操控光场传播[6];是主动共振系统,用极低功率光场即可实现巨克尔非线性效应[7];实现条件简单,可在微开或室温下实现[8];可调参数多,如控制场的强度、能级失谐量、原子数密度等[9]。由于以上这些新颖特性,研究者在理论和实验上对EIT系统的特性展开了研究,包括借助该体系实现超慢光传输[5]、存储[10],实现相位门[11]、光钟[12]、高效四波混频[13]、双稳态[14]和高维时空光孤子[15]等。另外,由于EIT系统的易控性以及光场传播方程与薛定谔方程的相似性,该体系也可作为量子模拟系统[16],模拟安德森[17]、Parity-time对称等模型[18]。
2005年,Segev小组利用双组分原子系统实现了Thirring模型[19],该模型首次由Walter Thirring在量子场论中提出[20]。具体形式是(-i∂vγv+mβ)ψ=±gγvψ(ψˉγvψ),方程的左边是Dirac方程的相对论协变形式,即薛定谔方程洛伦兹协变式,可化为
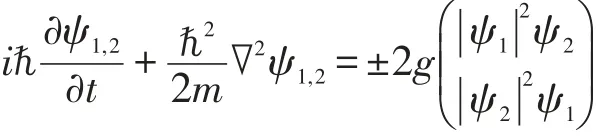
无量纲化可得
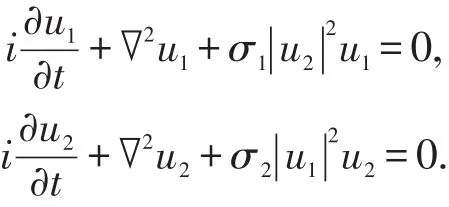
文章中,只需单组分的原子体系与两束光场即可构建探测场两个偏振分量所满足的Thirring模型。通过多重尺度方法,推导获得探测场满足的耦合非线性薛定谔方程组,选择合适的物理参数,实现了Thirring模型。在此基础上,讨论了(1+1)维模型中存在的基孤子对,说明该体系中孤子可稳定存在。与Segev小组提出的方案[19]相比,该体系的优点包括:(1)在激光场数目更少的情况下,只需单组分原子即可实现该模型;(2)由于利用探测场的两个偏振分量实现Thirring模型,故它们所满足的传播方程是完全对称的;(3)且该模型是矢量型Thirring模型。
1 模型
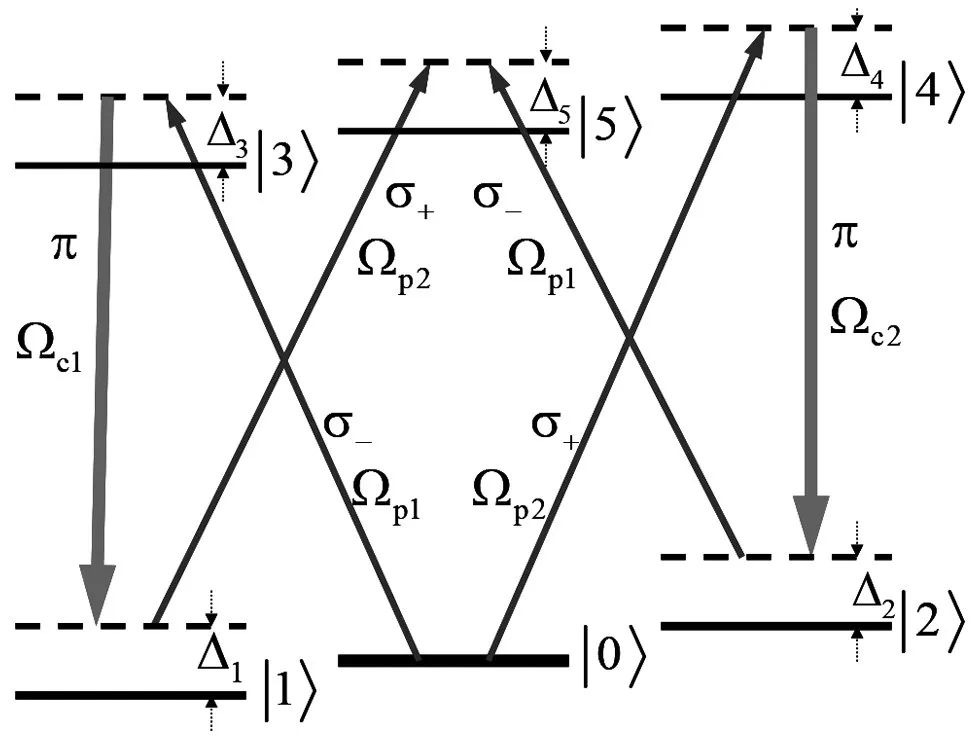
图1 半拉比频率为Ωcn的强连续控制场、半拉比频率为Ωpn的弱脉冲信号场与六能级原子系统相互作用的示意图,其中(n=1,2)。
选取的能级系统如图1所示,该体系由频率为ωp的弱线偏振探测场(可分解为半拉比频率为Ωp1的左旋偏振光σ-和半拉比频率为Ωp2的右旋偏振光σ+),频率为ωc1(半拉比频率Ωc1)和ωc2(半拉比频率Ωc2)的强控制场与六能级的原子系统构成。电场矢量写为
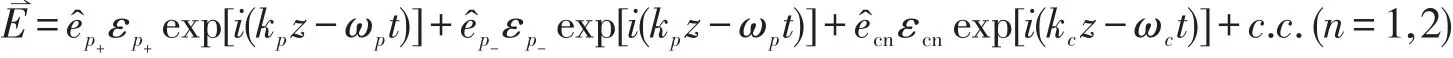
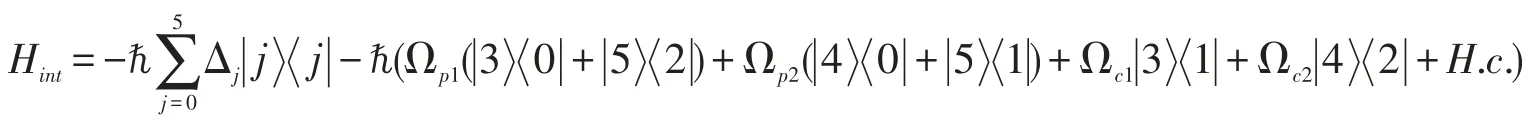
其中单光子失谐量Δ3,4=ωp-(ω3,4-ω0),双光子失谐量Δ1,2=ωp-ωc-(ω1,2-ω0),三光子失谐量Δ5=2ωpωc-(ω5-ω0),Δ0=0。在旋转波近似下,原子振幅Ai(i=0-6)满足的演化方程可写为
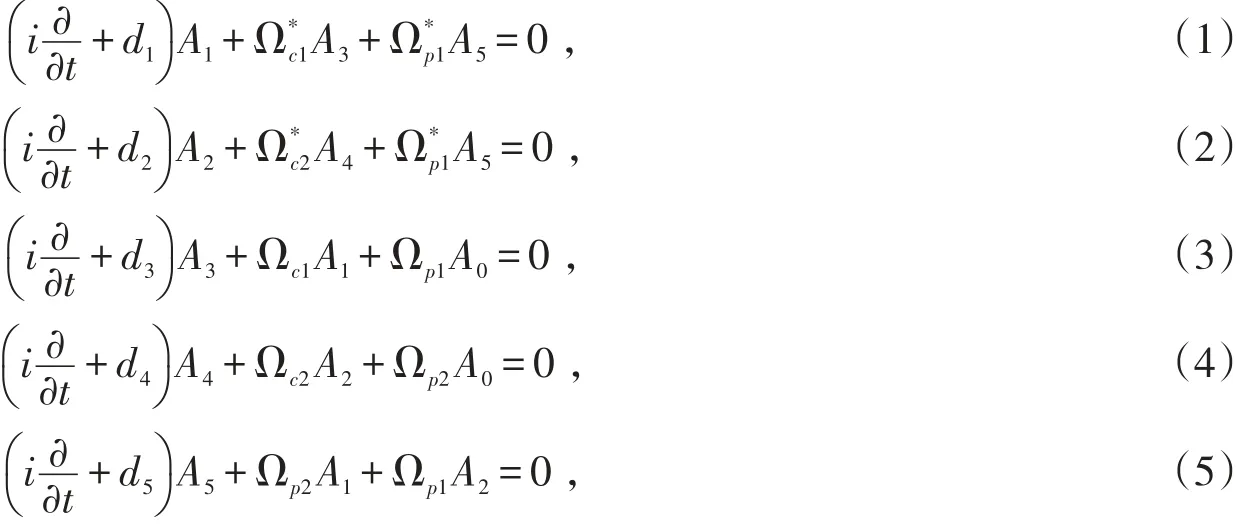
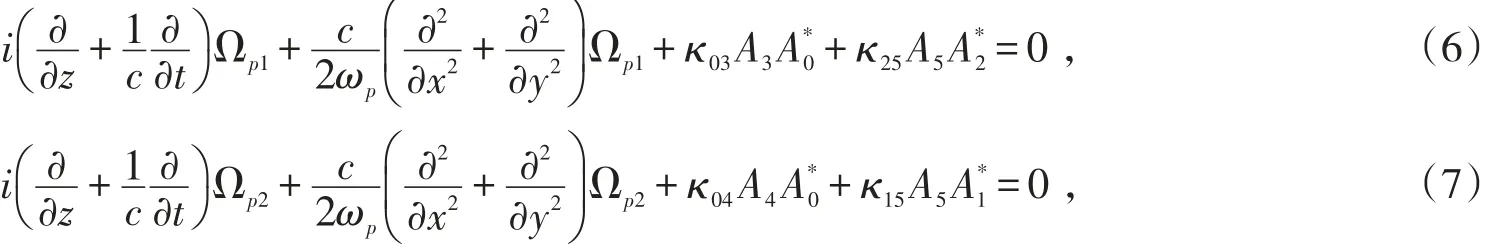
在该体系中,考虑脉冲宽度较宽,以至于原子能绝热地随光场演化,即可取绝热近似。这种情况下,可以忽略方程中的时间导数项;另一方面,考虑光场的横截面为一椭圆光斑,且其y方向的长轴长度远远大于x方向的短轴长,即方程(6,7)中y方向的衍射效应可以忽略。
2 Thirring模型的实现
麦克斯韦—薛定谔方程组(1-5)和(6-7)是耦合的非线性偏微分方程组,直接求解十分困难。故采用多重尺度方法将上述齐次的非线性偏微分方程组化为非齐次的线性偏微分方程组,从而求得该方程的解,给出探测场两个偏振分量的演化过程。
首先假设初始时原子布居在基态0,其损耗用小参数ε表征。在此基础下,对原子振幅与探测场包络作渐近展开:为避免发散,引入多尺度变量zl=εlz(l=0,2)和x1=εx。将上述展开式代入方程(1)和(2),可得一系列关于的迭代方程组。
在j=1时,探测场的解为

其中,k1,2=κ03,04d1,2/D1,2=β1,2+iα1,2,D1,2=|Ωc1,c2|2-d1,2d3,4,Fn是慢变量 z2的待定包络函数。
在j=2时,对探测场的包络函数不产生任何约束。
在j=3时,收敛条件使得探测场的包络函数满足耦合非线性薛定谔方程
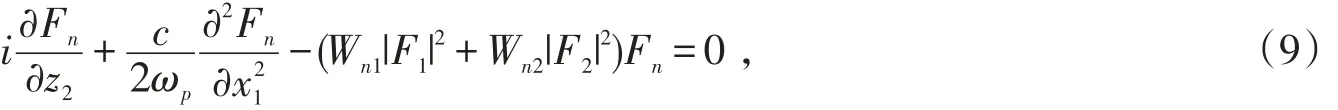
其中
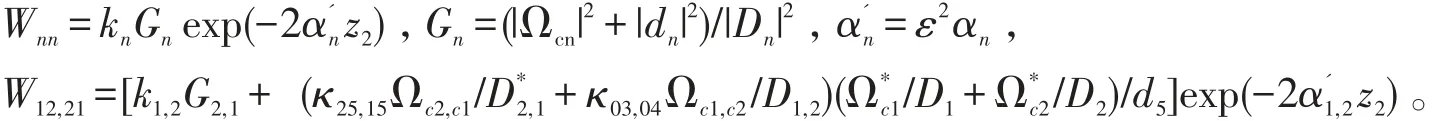
返回到原始变量并无量纲化,方程(9)可化为耦合的非线性薛定谔方程
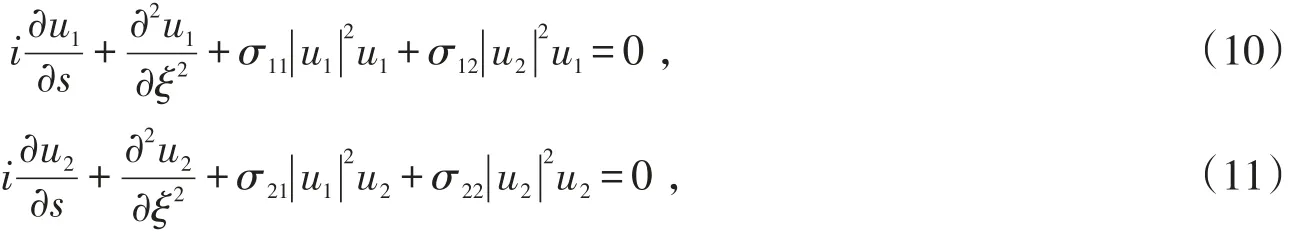
由于考虑的是相干原子系统,且为使实现Thirring模型的思路更简单,取一些物理与实验上均合理的假设和近似:(1)考虑实验上利用同一束控制场,即Ωc1=Ωc2=Ωc;(2)利用电磁感应透明效应中的量子干涉相消条件最后一个条件保证了自相位调制项远远小于交叉相位调制项,所以在该体系中,可利用失谐量Δ5来控制交叉相位调制项的大小;(3)取κ03=κ25=κ1,κ04=κ15=κ2。在这些条件下,得到可通过κ1,2来控制。
为了进一步说明问题,选取冷原子87RbD1线跃迁52S12→52P12的参数[21]为例,可取 γ0=Δ0=0,2γ1=2γ2=300s-1,2γ3=2γ4=2γ5=3.6×107s-1,ωp=2.37×1015s-1,Rx=2.52×10-3cm ,Ωc=6.0×107s-1,κ2=c0κ1=1.0×1011cm-1s-1,Δ1=Δ2=-3.0×104s-1,Δ3=Δ4=3.0×108s-1,Δ5=∓1.5×109s-1,其中c0是一自由参数,可通过偏振方向、电偶极跃迁矩阵元等调节。将上述参数代入方程(10,11)的系数表达式,可得典型衍射长度Ldiff=1.0 cm,典型拉比频率U0=3.67×106s-1,吸收系数α1=α2/c0=0.004 cm-1,非线性系数
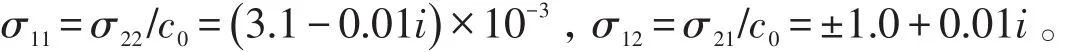
由上述参数可知,由于量子干涉效应,吸收系数α1,2、自相位调制项系数σ11,22以及交叉相位调制项系数σ12,21的虚部都可以忽略。故方程(10、11)可写为

上式与Thirring模型完全一致。通过具有电磁感应透明效应的原子介质成功实现了两种Thirring模型。在该方案中,只需两束激光场以及单原子体系即可实现;文献[19]中,若耦合方程完全对称,则自相位调制项不能忽略。考虑的系统中,虽然探测场两个偏振分量所满足的方程(12)与(13)是完全对称的,但自相位调制项仍然可以忽略。并且在该系统中,自相位调制项的大小可方便调节,并且该模型也可用来构造并实现Manakov模型。
3 Thirring模型的基孤子对解
这一部分将讨论方程(12、13)中存在的孤子对及其稳定性。设un=ψn(ξ)e-iβns,βn是传播常数,方程(12、13)可化为耦合的稳态方程组

该方程组可通过牛顿共轭梯度法[22]迭代求解,得到一系列孤子对及其功率曲线。
首先考虑交叉相位调制项同正时的情况。图2给出c0=0.4,1,1.6,2时,功率P随传播常数β的变化曲线。在c0取不同值时,通过图2中三条重合的蓝线可知第二个孤子ψ2的功率曲线不受传播常数的影响;第一个孤子ψ1的功率曲线随传播常数的变化趋势是单调递增,但增速不一,且图中给出各曲线对应的功率都随β→0而严格趋向于零。功率曲线严格给出了基孤子对的存在区间。
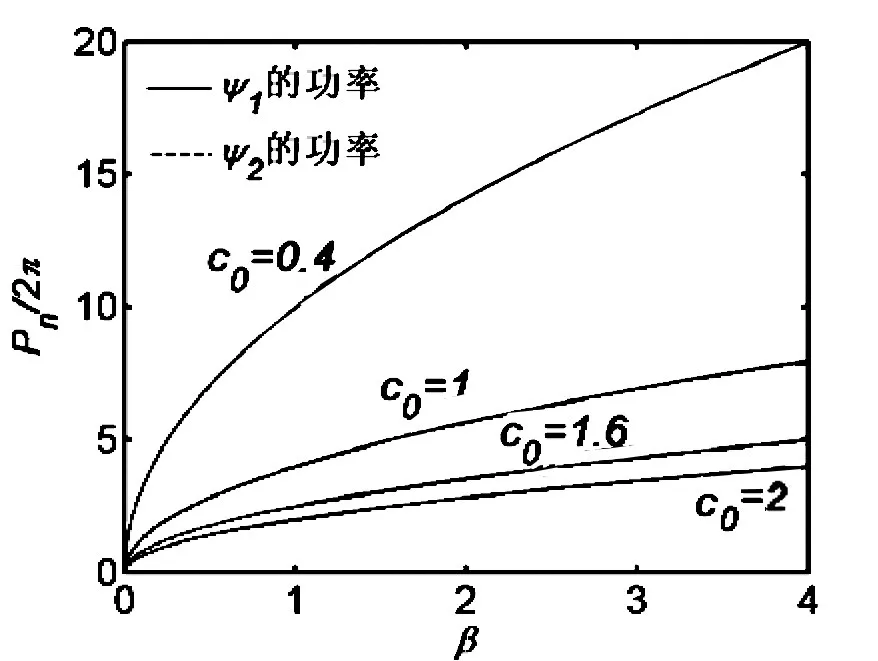
图2 功率随传播常数变化的曲线,红实线表示第一个孤子ψ1的功率,蓝虚线表示第二个孤子ψ2的功率。
(图中分别给出c0=0.4,1,1.6,2.0四种情况的功率曲线,且β1=β2=β)。
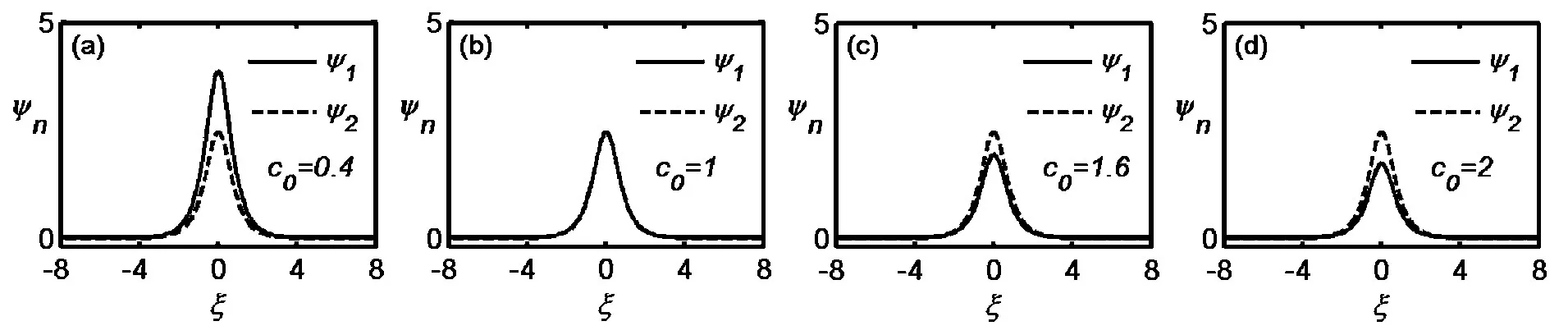
图3 基孤子对的轮廓图
图3给出传播常数β=3,c0取0.4,1,1.6和2时基孤子对的轮廓图。由图可知,随着c0的增加,ψ2的轮廓图不变,但ψ1的振幅逐渐变小。故可通过调节c0来达到控制ψ1,此即开光效应,为设计全光开关提供了一种全新的方案。在c0=1时,由于两个方程可看成两个退耦合的非线性薛定谔方程,故ψ1=ψ2。
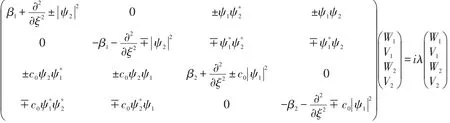
当λ的实部大于等于零时,孤子对稳定,反之该孤子对不稳定。通过分析c0从0.2到2的所有基孤子对的稳定性,发现这些孤子对在存在区域都是稳定的。
为了进一步验证孤子对的稳定性,将un(ξ ,s=0)=ψn(1+0.05ρ)(n=1,2)带入方程(12,13),利用分步傅立叶方法作传播,其中ρ表示分布在[0 ,1]之间的随机数。图4给出了加5%微扰后从s=0到s=200的传播俯视图,这四幅图分别对应于图3中的4对基孤子的传播结果,这些图再次说明了所得的基孤子对是完全稳定的。
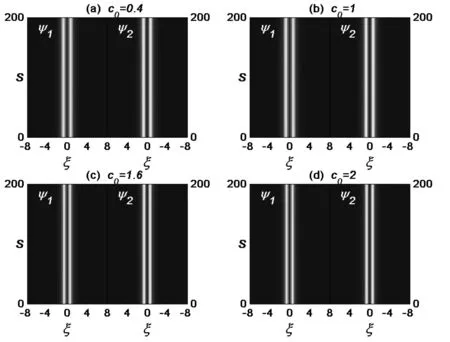
图4 基孤子对的传播图。(a)、(b)、(c)和(d)分别对应c0=0.4,1,1.6,2的结果。
同时,找到了交叉相位调制项系数同负时该体系的暗暗孤子对,但所得孤子对不是完全稳定的,故在此不再展示。
4 结论
借助电磁感应透明介质,实现了探测场两个偏振分量满足的矢量Thirring模型。在该方案中,仅需一种原子和两束激光场,且所得的耦合方程是完全对称的。在此基础上,讨论了该体系中存在的孤子及其稳定性,发现所有基孤子对在存在区域都是稳定的,不依赖于参数c0的选取。借助该体系还可研究暗暗孤子对以及构建(2+1)维和(3+1)维的Thirring模型。
[1]T.H.Maiman.Stimulated optical radiation by ruby[J].Nature,1960,187:493-494.
[2]N.Bloembergen.Nonlinear Optics[M].New York:Benjamin,1965.
[3]S.E.Harris.J.E.Field,A.Imamoglu.Nonlinear optical processes using electromagnetically induced transparency[J].Phys.Rev.Lett,1990,64:1107-1110.
[4]S.E.Harris.Electromagnetically induced transparency[J].Phys.Today,1997,50:36-42.
[5]L.V.Hau,S.E.Harris,Z.Dutton,and C.H.Behroozi.Lightspeed reduction to 17metresper second in an ultracold atomic gas[J].Nature,1999,397:594-598.
[6]C.Hang,G.Huang.Stern-Gerlach effectofweak-lightultraslow vectorsolitons[J].Phys.Rev.A,2012,86:043809.
[7]H.Schmidt,A.Imamoglu.GiantKerrnonlinearitiesobtained by electromagnetically induced transparency[J].Opt.Lett,1996,21:1936-1938.
[8]M.M.Kash,V.A.Sautenkov,A.S.Zibrov,L.Hollnerg,G.R.Welch,M.D.Lukin,Y.Rostovtsev,E.S.Fry,and M.O.Scully.Ultraslow group velocity and enhanced nonlinearopticaleffects in a coherently driven hotatomic gas[J].Phys.Rev.Lett,1999,82:229-5232.
[9]H.J.Li,Y.P.Wu,C.Hang,and G.Huang.(3+1)-dimensional superluminal spatiotemporal optical solitons and vortices atweak light level[J]. Phys.Rev.A,2012,86:043829.
[10]D.F.Phillips,A.Fleischhauer,A.Mair,R.L.Walsworth,M.D.Lukin.Storageof lightin atomic vapor[J].Phys.Rev.Lett,2001,86:783-786.
[11]D.Petrosyan,M.Fleischhauer.Quantum information processingwith single photonsand atomic ensembles inmicrowave coplanarwaveguide resonators[J].Phys.Rev.Lett,2008,100:170501.
[12]R.Santra,E.Arimondo,T.Ido,C.H.Greeme,J.Ye.High-accuracy optical clock via three-level coherence in neutral Bosonic88Sr[J].Phys.Rev. Lett,2005,94:173002.
[13]Y.Zhang,A.W.Brown,M.Xiao.Opening four-wavemixingand six-wavemixing channelsvia dualelectromagnetically induced transparencywindows[J].Phys.Rev.Lett,2007,99:123603.
[14]A.Joshi,M.Xiao.Atomic opticalbistability in two-and three-levelsystems:perspectivesand prospects[J].J.Mod.Optic.2010,57:1196-1220.
[15]H.J.Li,Y.P.Wu,and G.Huang.Stableweak-lightultraslow spatiotemporalsolitonsviaatomic coherence[J].Phys.Rev.A 2011,84:033816.
[16]L.Stefano.Quantum-opticalanalogiesusing photonic structures[J].Laser&Photon.Rev.2009,3:243-261.
[17]J.Cheng,G.Huang.Controlling the delocalization-localization transition of light via electromagnetically induced transparency[J].Phys.Rev.A 2011,83:053847.
[18]C.Hang,G.Huang,and V.V.Konotop.PTsymmetrywith a system of three-levelaoms[J].Phys.Rev.Lett.2013,110:083604.
[19]I.Friedler,G.Kurizki,O.Cohen,and M.Segev.Spatial Thirring-type solitons via electromagnetically induced transparency[J].Opt.Lett.2005,30:3374-3376.
[20]W.Thirring.A soluble relativistic field theory[J].Ann.Phys.1958,3:91-112.
[21]J.Yang.NonlinearWaves in Integrableand Nonintegrable Systems[M].SIAM:Philadephia,2011.
The Realization of Vector Thirring Model Via Electromagnetically Induced Transparency
ZHANG Kun,LIHui-jun
(DepartmentofPhysics,Zhejiang NormalUniversity,Jinhua,Zhejiang,321004,China)
We propose a scheme to construct a Thirringmodel via electromagnetically induced transparency(EIT).The system we consider is a cold,resonant atomic gas with a six level configuration and interacting with probe and control fields.We show thatunder EIT condition the probe field envelope obeysa coupled nonlinear Schr[o]dinger equations,which become a Thirring model when the system parameters are suitably chosen.In the Thirringmodel,the ground soliton pair solution are presented.And the stability is also discussed.Comparing with the previous study,the presentscheme usesonly a single atomic species and two beams of laser field,hence is easy for the physical realization;On theotherhand,thereexistsdark-dark soliton pairsolution.
Thirringmodel;Electromagnetically induced transparency;Multi-scalesmethod;Cross-phase modulation;Soliton
O437
A
1008-9659(2016)02-0039-06
2016-04-01
国家自然科学基金资助项目(11204274,11574274);浙江省自然科学基金资助项目(LY15A040002,LZ15A050001)。
张 昆(1989-),男,浙江宁波人,硕士研究生,主要从事非线性物理与非线性光学研究。
*[通讯作者] 李慧军(1980-),男,山西忻州人,副教授,主要从事非线性物理与非线性光学研究。

