解析抛物线 y=ax2+bx+c 中系数在图象中的作用——小组合作中的电子白板教学设计

◆张锋

解析抛物线 y=ax2+bx+c 中系数在图象中的作用
——小组合作中的电子白板教学设计

◆张锋

10.3969/j.issn.1671-489X.2016.17.095

以解析一元二次方程中系数的作用为例，教师在组织教学的时候，需把大纲、教材、学生学情、电子白板的运用进行全面、系统融合，在头脑中勾勒出实现目标清晰的路线图，需设计好对电子白板功能的使用安排。只有对整个交互过程进行细致规划，才能让学生理解清楚、操作准确、验证无误。

电子白板；教学设计；

1 引言

在进行一元二次方程二次方系数作用的解析教学时，如何引领学生对方程中系数所起的作用进行细致、全面的分析，对不少教师来说是一件比较麻烦的事情。传统的教学多采用黑板演示的办法，常常会因烦琐的推导、滞后的绘图影响学生的理解程度。如果借助电子白板，就可以使运算的推导、图象的变化有机协调起来，让学生形成清晰的印象。笔者在此谈谈自己的教学设计。

2 教前分析

1）教材分析：本节内容属于鲁教版四年制初四第一学期第二章，属于“二次函数”中“二次函数 y=ax2+bx+c 的图象与性质”的内容。学习本章内容之前，学生已经学习了二次函数概念、y=ax2函数的图象与二次函数 y=ax2+bx+c的图象和部分性质，对于二次函数已经有所认识。

2）学情分析：初四的学生对图形变化的规律已积累了一定的学习经验，但图形探究对他们来说仍属于难点，对数形结合等许多问题还需放在小组内通过合作探究来完成。

3）白板分析：本节课对于 a、b、c的性质的探索，是建立在图象的动态变化上的，交互式电子白板所附带的功能，为“教”与“学”提供了必要的支持，可以提高学生的兴趣，能为化解难点提供帮助。因此，电子白板是展开教与学活动的首选媒体。

3 目标及重难点

1）学习目标：掌握 a（或 b、c）的变化对于二次函数y=ax2+bx+c 的图象变化产生影响的规律；感悟新旧知识间的关系，深刻体会数形结合的思维方式，探究、分析、归纳由特殊到一般的规律性解题方法和过程；体会数形结合的思想，发展图象思维能力，能积极参与数学学习活动，不断提升对数与形的理解和认识水平。

2）学习的重难点：掌握 a（或 b、c）的变化对于二次函数 y=ax2+bx+c 的图象（顶点坐标、对称轴、开口方向、开口大小等问题）变化产生影响的规律。

4 教学过程设计

1）导入：教师利用白板出示具体问题，让学生进行人机互动，最后出示答案。二次函数 y=3（x-1）2+5 开口向（ ），顶点坐标为（ ），对称轴为（ ）。当x＞l时，y随x的增大而（ ）；当 x＜ 1 时，y随 x的增大而（ ）。因为 a=3 ＞ 0，所以 y有最（ ）值；当 x=（ ）时，y最（ ），值是（ ）。

2）指导学生操作二次函数图象，利用电子白板，教师示范后学生操作，让学生初步了解改变二次函数 y=ax2+bx+c中 a、b、c 的值，函数图象随之变化的现象。

【探究活动1】师生利用白板互动，通过电子白板改变a，观察图象的开口大小和方向随 a的变化规律。

①设二次函数 y=ax2：a（先假设 b=0，c=0）为离散型数字，探究a的值与抛物线开口方向的关系，记录白板上动态数据，通过观察发现图象间断性变化的现象。

使 a=1、2、3、4、5、6，观察图象的变化，记录每次的结果，分析a对图象的影响，用文字表达二次函数y=ax2+bx+c 中 a 的值与抛物线开口大小的关系，小组讨论后得出结论：a的值越大，开口越小。

使 a=-1、-2、-3、-4、-5、-6，观察图象的变化，记录每次的结果，分析a对图象的影响，用文字表达二次函数 y=ax2+bx+c 中 a 的值与抛物线开口大小的关系，小组讨论后得出结论：|a| 的值越小，开口越小。

② a（先假设 b=0，c=0）为连续型数字，使 a 自 0 开始逐渐增大（如 1≤a ≤ 10），观察图象的变化，并记录结果，分析 a 对图象的影响，用文字表达二次函数 y=ax2+bx+c 中a的值与抛物线开口大小的关系，小组讨论后得出结论：a的值越大，开口越小。

③使 a 自 0 开始逐渐减小（如：-10 ≤ a ≤ -1），观察图象的变化，并记录结果。分析a对图象的影响，用文字表达二次函数 y=ax2+bx+c 中 a 的值与抛物线开口大小的关系，小组讨论后得出结论：|a| 的值越大，开口越小。

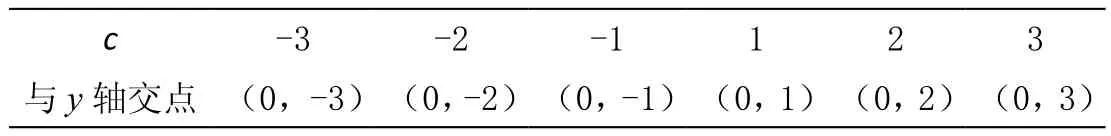
表1

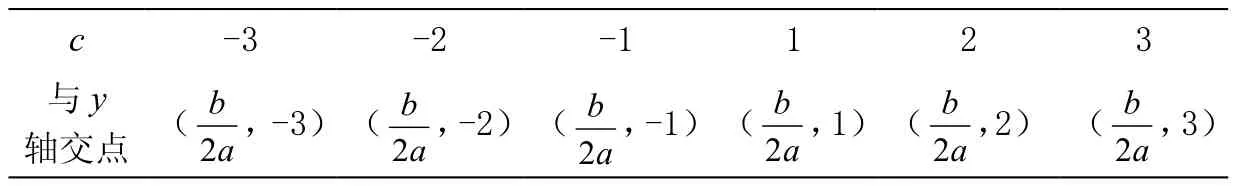
表2

表3

归纳结论：二次函数 y=ax2+bx+c 中 a 的值与抛物线开口大小的关系是 |a| 的值越大，开口越小。

【探究活动 2】改变 c的值，教师在白板上利用电子白板实施c的变化，师生利用白板互动，观察c沿着对称轴上下移动的规律。

①假设 b=0，任意取定 a 的值，使 c=±1、±2、±3 等离散数值，观察图象的变化，记录每次的结果，并且算出此时图象与 y轴的交点的纵坐标（表 1），分析 c对图象的影响，用文字表达二次函数 y=ax2+c 中，c 的值与抛物线与y轴交点的关系。

教师引导学生讨论，得出结论：二次函数 y=ax2+c 中，抛物线与 y 轴交点的坐标是（0，c）。

②假设 b=0，任意取定 a 的值，使 c 取某一范围内的连续数值（如：-10 ≤ c ≤ 10），观察图象的变化，分析 c对图象的影响，用文字表达二次函数 y=ax2+c 中，c 的值与抛物线与y轴交点的关系。

引导学生归纳结论：当 a、b确定时，决定了函数图象的顶点，c的变化决定图象的上下平移。

③任意取定a、b的值，使c=±1、±2、±3等离散数值，观察图象的变化，并记录每次的结果，并且算出此时图象与 y轴的交点的纵坐标（表 2），分析 c对图象的影响，用文字表达二次函数 y=ax2+bx+c 中，c 的值与抛物线与 y 轴交点的关系。

引导学生归纳结论：当 a、b确定时，决定了函数图象的顶点，c的变化决定图象的上下平移。

【探究活动 3】改变 b的值，观察 b在平行于 x轴的直线上左右移动的变化规律。

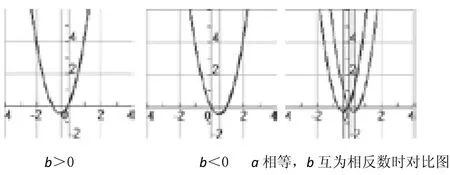
图1

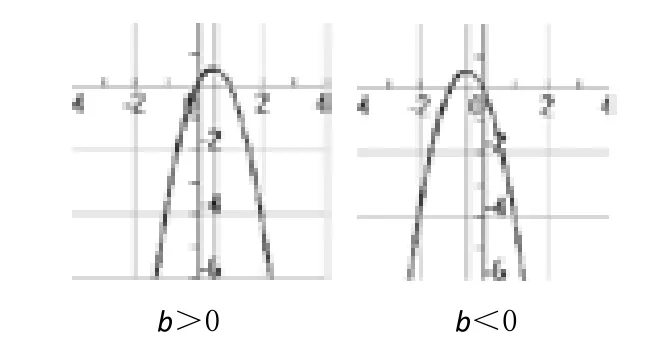
图2

①当 a 取大于 0 的值时，假设 c=0，使 b=±1、±2、 ±3等离散数值，记录每次的结果，画出抛物线的对称轴，分析b对图象的影响，如图1所示。

引导学生总结，用文字表达二次函数 y=ax2+bx 中 a、b的值与抛物线对称轴的关系。

②当 a 取小于 0 的值时，假设 c=0，改变 b 的值，使b=±1、±2、±3，观察图象的变化，记录每次的结果，并画出抛物线的对称轴，分析b对图象的影响，如图2所示。

③当a取大于0或小于0的值时，任意取定c的值，使 b 取得某范围内的连续数值（如：-10 ≤ b ≤ 10），记录每次的结果，画出抛物线的对称轴，分析b对图象的影响。

3）归纳总结：教师利用白板现场与学生互动，对本节课知识点进行总结，形成本节课的知识树，强调本节课知识重难点。学生之间可以互相讨论，交换意见，分析归纳其特点，完成表3。

4）练习反馈：出示问题，让学生在应用中加深理解，培养严谨的数学思维能力。

5 结语

在本节教学中，a、b、c 是不断变化的，需要不断地画图进行比较。为了弥补常规教学不能展示图形连续变化的不足，通过利用电子白板，直接有效地展示图形变化，帮助学生建立深刻的感性认识，有助于理解、学习、掌握数形变化的规律。■

G623.5

B

1671-489X(2016)17-0095-03

作者：张锋，淄博市临淄区朱台镇桐林小学，一级教师（255432）。