基于三维Taylor模型的福建及邻近地区地磁模型研究
张素琴, 付长华, 赵旭东
中国地震局地球物理研究所, 北京 100081
基于三维Taylor模型的福建及邻近地区地磁模型研究
张素琴, 付长华, 赵旭东
中国地震局地球物理研究所, 北京100081
摘要基于福建及邻近地区高密度的256个地磁场矢量(D、I、H分量)实测数据,结合全球陆地1 km基准海拔高度工程的网格数据以及最新的第十二代国际地磁参考场模型(IGRF12),采用三维Taylor多项式模型构建了福建地区的地磁场模型.通过比较均方偏差(RMS)、磁场实际分布以及残差等,结果显示: (1) 当三维Taylor模型的截断阶数(N)为2时,可基本反映N为6时的二维Taylor模型的拟合效果; (2) 三维Taylor模型计算方便,精度较高,但较易出现龙格现象,因此在确定截断阶数时既要考虑模拟精度,还需要考虑边界效应问题.
关键词地磁场模型; 三维Taylor多项式模型; 福建及邻近地区; 均方偏差
1引言
地磁场是一种全球性的地球物理场,它既是时间也是空间的函数,人们通常采用地磁场模型来描述它的时空变化特征.地磁场模型在地球物理勘探、地球深部研究、空间科学、军事导航等许多领域有着广泛的应用.地磁场模型包括全球磁场模型和区域磁场模型.由于地磁场具有区域性变化特征,而全球磁场模型无法对区域磁场的变化进行精细准确的描述,因此世界各国的学者会根据实际需求和研究需要建立不同区域的地磁场模型.
常见的区域磁场模型有球冠谐模型、矩谐模型、Taylor多项式模型、Legendre多项式模型、曲面Spline模型等.国内外众多学者曾利用这些区域磁场模型对不同区域磁场做过研究.Haines(1985)利用球冠谐模型分析了加拿大地区1960—1983年的地磁场长期变化情况;Thébault等(2004,2006)和Thébault等(2008)在对原有的球冠谐模型改进的基础上研究了法国地区的地磁场(Thébault,2008);Alldredge(1982)利用矩谐模型和柱谐模型对比研究了美国东南部区域磁场; Düzgit等(1997)利用欧洲地区42个地磁台站的年均值数据基于矩形多项式分析研究了欧洲区域的地磁场变化;冯彦等(2013a)基于墨西哥国内磁测数据,对比分析了基于CM4、Taylor多项式及曲面Spline模型计算的地壳磁异常场的不同.国内学者主要针对地磁场建模方法进行探讨,并基于各种模型对中国及中国部分地区地磁场开展了研究工作.安振昌和徐元芳(1981)将曲面Spline方法引入了地磁区域建模领域,并取得了较好的效果.徐文耀等(2011)从地磁场误差理论出发,重点对球谐模型和球冠谐模型的误差特征及来源进行了分析,讨论了各自的优缺点及减少误差的途径.区家明等(2012)利用Legendre多项式模型研究了小尺度区域的地磁场建模技术.Feng等(2015)运用基于Taylor和Legendre多项式的数据拟合模型对区域模型截断水平和边界效应的选取进行了研究.这些都为模型的选取和运用提供了指导性的建议.徐文耀和朱岗昆(1984)推广了Alldredge提出的局部地区地磁场矩谐分析方法,导出了既包含内源场又包含外源场的矩谐级数表达式,研究了1970.0年我国及邻近地区的地磁场分布特征;徐文耀和朱岗崑(1985)又用矩谐分析方法建立了中国及邻近地区地磁场的三维模型,研究了中国及邻区地磁场三维分布,以及地磁场的长期变化特征;安振昌(2000)利用球冠谐模型模拟了青藏高原的磁异常场分布;陈斌等(2011)应用球冠谐和方法,基于中国地区的实测数据,建立了2005—2010中国地区地磁场长期变化模型.
相对于上述其他模型,Taylor多项式模型由于其计算简单、使用方便,且适于表示区域的地磁场分布情况,因此仍然是目前使用较为广泛的一种模型.安振昌等(1991a)利用Taylor多项式模型建立了1950.0—1980.0年代中国地区主磁场模型,分析研究了局部地区地磁场泰勒多项式模型的特点;徐元芳等(1992)利用泰勒多项式建立了1950—1985年中国地区地磁场长期变化模型,研究了1950年以来中国地区地磁场长期变化的趋势;徐文耀等(2005)采用泰勒级数法建立了2000年代中国地磁场各要素长期变化模型CGRF-SV,研究表明中国地区地磁长期变化与全球长期变化的总趋势基本符合,但是,CGRF-SV表现出一些特有的局部异常特征;高金田等(2005)以2003年中国地磁观测数据为基础,利用泰勒多项式模型得到了中国地磁正常场,计算并分析了中国地磁异常场的分布;乔玉坤等(2008)在对现有地磁场建模方法及适用性研究的基础上,选取泰勒模型对某区域磁场总场进行了拟合分析.冯彦等(2013b)基于实测数据,结合地磁综合模型(CM4)和泰勒多项式分析了中国地区主磁场的年变率分布情况.
通常研究所用的Taylor模型多为二维模型,未考虑高度因素的影响,无法反映地磁场随高度的变化.研究表明,地磁场强度一般随着高度的上升约以20 nT/km的速率近似线性减小(安振昌,1991b;冯彦,2013c).鉴于此,柳士俊等(2011)通过增加高度项,提出了三维Taylor多项式模型,从而有效地提高了模型的精度.蒋勇等(2015)基于该模型,应用CHAMP卫星数据,建立了中国及邻近地区三维磁场模型.
由于研究需要,1960年我国在福建及邻近区域进行了高密度、高精度的地磁三分量(水平分量H、磁偏角D和磁倾角I)测量,该区域的测点密度要远高于其他区域.本研究拟基于福建及其邻区的地磁实测数据,利用三维Taylor模型建立并分析该区域的地磁场.在建模时截断阶数的选取和边界效应的控制是两个关键问题.文中三维Taylor模型是在二维模型的基础上建立的,因此将两者的RMS、磁场分布及残差分布比较分析,来确定三维模型的最佳截断阶数,最后给出相关结论和讨论.
2数据与方法
2.1实测数据及补充点的选取
本文使用的是1960.0(即将1960年野外磁测资料经过日变化通化及长期变改正,统一归算至1960年1月1日,通常记为1960.0)年福建及邻近地区的256个地磁实测点的H、D、I分量资料.由于缺少周边及海洋地区的磁测资料,利用2014年12月最新发布的第12代国际参考地磁场IGRF12 (http:∥www.ngdc.noaa.gov/IAGA/vmod/igrf.html)模型均匀添加了1960.0年的18个补充点,以期改善边界效应.研究范围为22.5°N—28.5°N,115.5°E—121°E,所有测点的分布如图1所示.

图1 福建及邻近地区地磁测点分布图Fig.1 Distribution chart of all measured data over Fujian and its adjacent areas
2.2Taylor多项式模型
通常使用的二维泰勒模型表达式如下:
(1)
式中W表示任意磁场要素;N为截断阶数;φ,λ为各地磁测点的纬度和经度;φ0,λ0为多项式的展开原点的纬度和经度,Aij为相应各分量的模型系数,每个模型有N(N+1)/2个系数,所有系数通过最小二乘法求取.
本文基于上述二维模型,通过添加高度项,并通过系数的完整展开而得到三维Taylor模型,通过完整展开可以用较低的截断阶数反映出更多的地磁场信息.其表达式如下(柳士俊等,2011):

(2)
式中的参数含义和(1)式相同,区别在于增加了高度项,而h为各地磁测点的海拔高度;φ0,λ0,h0为福建及其邻近地区的展开原点坐标,其中φ0=25.5°N、λ0=118.25°E、h0=243.45 m;Aijk为相应各分量的模型系数,每个模型有N3个系数,所有系数通过最小二乘法求取.
三维模型与二维模型的区别除了添加高度项外,在系数的展开形式上也不同.二维模型的系数是按照经典展开,最后获得一个三角矩阵,而三维模型按照完整展开,最后获取的是一个方阵.理论而言三维模型的系数更多,所反映的磁场信息也更多.
2.3测点高度的选取
通过网站http:∥www.ngdc.noaa.gov/mgg/topo/中的“全球陆地一公里基准海拔高度工程”的网格数据获得到间隔为1弧分的高程网格值,并利用“最近点选取法”(选用与每个实测点最近的网格值)得到每个对应测点的高度值,位置误差不超过0.0083°(约0.92 km).图2为福建及邻近地区的高程网格分布.
3结果
3.1截断阶数的确定
建立磁场模型的关键是如何确定合适的截断阶数.区域磁场模型通常通过提高截断阶数来提高模型的精度,截断阶数越大,空间分辨力越高,模型值与实测值的误差就越小,然而,过高的截断阶数在增加计算量的同时,还会使结果出现畸变,即所谓的“龙格现象”(李岳生和黄友谦,1978).提高区域磁场模型的精度和改善边界效应似乎是一个相互矛盾的问题(杨云涛,2009).因此,对截断阶数的定量确定是一件困难的事.通常采用比较不同截断水平的结果,结合物理意义和实测值,选取结果稳定的截断水平,具体主要依据以下两条确定截断阶数(安振昌,2001;乔玉坤等,2008):一,区域地磁场模型的均方偏差要小于IGRF的均方偏差.也就是说,对于某一地区,区域地磁场模型应比全球模型能更好地反应建模区域地磁场的分布;二,随着截断阶数的增加,均方偏差(RMS)会逐渐减小,当RMS基本趋于稳定时,可确定模型的截断阶数.其中,RMS可通过下式得到:
(3)
其中,Wmod为任意地磁要素的模型值,Wobs为相同地点同一地磁要素的观测值,n为观测点数量.
通过与二维Taylor多项式展开精度对比来确定三维Taylor多项式的截断阶数.图3给出1~10阶的三维和二维模型的H、D和I分量的RMS变化.
根据图3,二维模型(实线)在截断阶数N<6时,H、D和I分量的RMS随N的增大而迅速减小,平均下降幅度达到了72.28%,其中H分量由1阶的582.82 nT下降到5阶的174.79 nT,D分量从1阶的0.458°减小到5阶的0.199°,I分量从2.330°下降到了0.225°;当N在6~10时,RMS平均减少幅度只有5.87%,逐渐趋于平稳;当N>10时,二维模型的RMS出现了突然放大的现象(考虑到与三维模型做比较,且二维模型的截断阶数一般都不会超过10,因此上图未列出N>10的变化).三维Taylor多项式模型(虚线)的RMS在N=5时基本达到最小,其中H分量为129.10 nT,D分量为0.170°,I分量为0.294°.当N>5时,由于完全展开所计算的系数超过了125个,远多于5阶二维非完全展开的15个系数,当超过5阶时,由于系数太多,三维模型出现了“龙格现象”,导致了RMS突然放大,H分量达到13374.85 nT,D分量达到0.778°,I分量达到13.310°.
观察N为1~5时两者的RMS变化.三维模型的RMS均小于对应二维模型的RMS值.由式(1)和式(2)可知,三维模型共有N3个系数,而二维模型却有N(N+1)/2个系数.因此认为在模拟福建地区地磁场时,较低阶的三维Taylor模型可反映更多的地磁场信息,其精度相当于中或高阶的二维模型.
由于图3三维模型在N=5后出现了RMS值的突增,为了更清楚地观察两种模型针对不同N的变化,图4列出了N=1~5时所对应的RMS变化.
从图4可清楚地发现,二维模型(实线)从N=1增加到2时,其RMS值快速下降,其后下降速度变缓.对于三维模型(虚线)而言,同样当N变化至2时,出现了大幅下降,其后下降速度变慢,但是I分量在N=5时出现了上升.

图2 福建及邻近地区的三维高程Fig.2 3D elevation map of Fujian and its adjacent areas
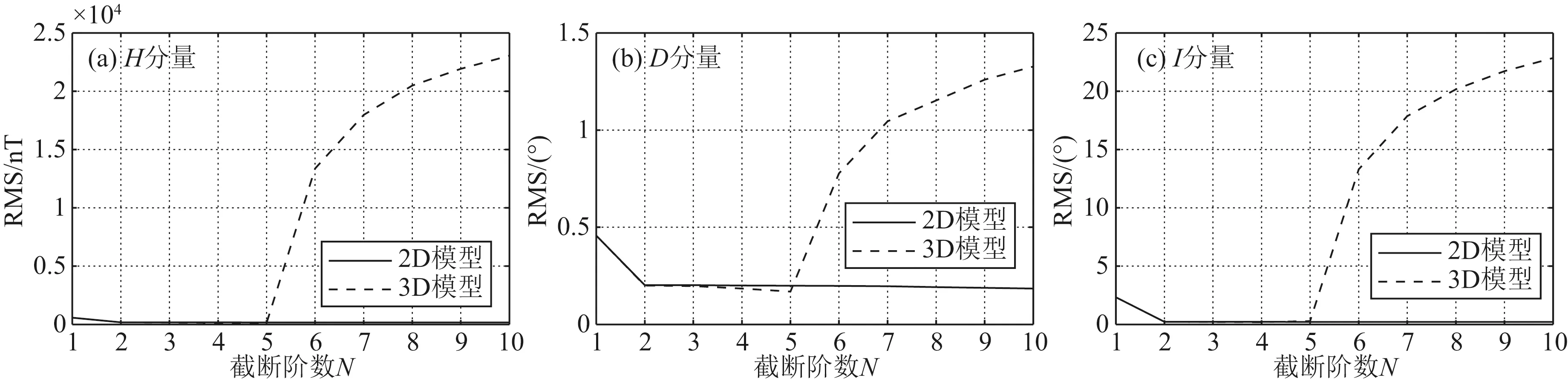
图3 N=1~10时二维和三维模型RMS的变化Fig.3 The RMS variation between 2D and 3D models while N=1~10

图4 N=1~5时二维和三维模型RMS的变化Fig.4 The RMS variation between 2D and 3D models while N=1~5
为了确定合适的三维模型截断阶数,表1列出了两种模型的各阶RMS数值.根据表1,二维模型当N=6时基本趋于稳定,虽然稳定区可取到N=10,但误差水平没有实质性的改善,且要以计算量的提高为代价;而三维模型当N=5时I分量出现了增加,当N>6时则三分量都出现了大幅增加,H和I分量出现了约2个数量级的增加,D分量也增加了约3倍.综上可初步确定二维模型的可选阶数为6~10,而三维模型的可选阶数为2~5.

表1 二维和三维模型的RMS值
3.2基于三维模型的福建及邻近地区的地磁场分布
若想确定合适的N,除了考虑精度问题,还应考虑边界效应.也就是说,在增加截断阶数以提高模型精度的同时需要考虑阶数增大带来的边界效应问题.基于上述初步分析结果,分别绘制了N=2~5时的福建及邻近地区的地磁场网格三维分布图,发现当N=2~5时东南地区(台湾地区)都存在一定的畸变,由于该区域地势较高(图2),又缺乏地磁实测数据,结果只是通过三维模型计算得到,因此是否真的存在磁异常还有待进一步实测验证.因篇幅所限,且N=2更接近实际情况,只给出2阶三维模型的磁场分布,如图5所示.
根据图5,H分量在福建及邻近地区的地磁场分布分别随着纬度的增加,强度由35000增加至38000 nT左右;D分量在福建及邻近地区的分布都为负值,从西南向东北方向,强度由-0.8°减少至-3°左右;I分量在福建及邻近地区的分布都为正值,随着纬度的增加,强度由30°增加至41.5°左右.
通过绘制各阶二维模型的分布,发现当N=6时,和图5的分布最为接近.由于相似性较高,故在此不再给出二维模型的磁场分布图.综合考虑模型拟合精度及边界效应问题,进一步确定三维Taylor多项式的截断阶数取2较为合适.
上文提到确定截断阶数的另外一条主要依据是,区域地磁场模型的均方偏差要小于IGRF的均方偏差.因此,又利用最新的IGRF12模型计算了所有实测点位置D、I、H的模型值,并计算了模型值与实测值的均方偏差RMS,表2列出了IGRF12模型、6阶二维模型、2阶三维模型三种模型的RMS.
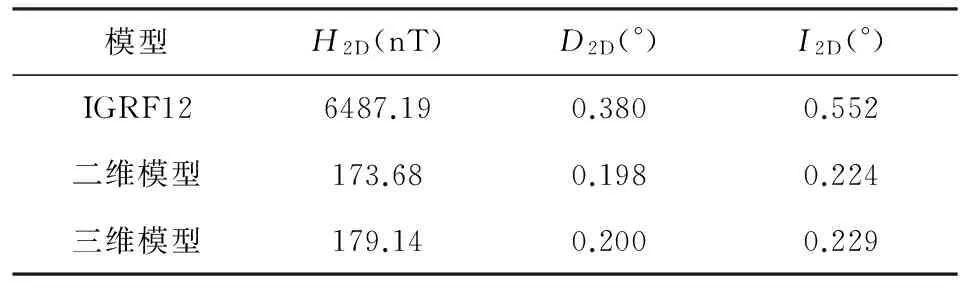
表2 IGRF12、二维和三维模型的RMS值
由表2可见,二维(N=6)模型、三维(N=2)模型的RMS均远远小于IGRF12的RMS,因此对于福建及邻近地区的二维Taylor模型取6阶、三维Taylor模型取2阶比较合适.
为了便于比较,表3和表4分别给出了2阶三维模型的系数和2阶二维模型的系数.
对比发现,两种模型的首项系数非常接近,该系数是其他系数大约3个乃至更高的数量级.由于首项系数决定了模型拟合值的主要特征,这也是两种模型的分布及强度较为相似的主要原因.比较两种模型的公式,三维模型的系数约为二维模型的2N倍,因此理论上前者比后者能反映更多的信息.

图5 福建及邻近地区的三维Taylor模型的地磁场分布(N=2)Fig.5 The geomagnetic field distribution of Fujian and its adjacent areas base on 3D Taylor model (N=2)

表3 2阶三维模型的系数

表4 2阶二维模型的系数
3.3模型误差分析
验证所建模型的可靠性,通常考察其与实测值的拟合程度是较为直观的方法.由于考虑了高度因素,理论上三维模型的拟合会好于二维模型的.所有256个实测点与对应二维、三维模型拟合值的比较见图6.

图6 所有测点及二维(N=6)、三维(N=2)模型值相比较Fig.6 The comparison among all measured data, 2D (N=6) and 3D (N=2) model values

图7 二维(N=6)、三维(N=2)模型的残差值的比较Fig.7 The comparison of residuals between 2D (N=6) and 3D (N=2) model values
从图6发现6阶二维模型(绿线)和2阶三维模型(红线)与所有实测点的拟合度较高,尤其是I分量.为了进一步观察两模型与实测值的接近程度,图7列出了两种模型与实测值的所有点的残差.
观察图7发现无论从残差幅度还是残差变化的趋势看,两种模型相对实测点的接近程度高度一致,因此从图6和7也验证了2阶的三维模型基本能达到6阶二维模型的精度.
4结论与讨论
本文基于1960.0年的福建及邻近地区地磁三分量实测数据,分别运用二维和三维Taylor多项式模型计算并绘制了福建及邻近地区的地磁场分布,对比分析了两种模型的磁场分布、RMS与残差分布等结果,得出以下结论.
(1) 与二维Taylor多项式模型相比,三维Taylor模型增加了对高度因素的考虑.在福建及邻近地区,海拔高度范围为-0.5~1.16 km左右,故磁场强度应有-10~20 nT左右的误差,因此三维Taylor模型在精度上要好于二维模型.本研究使用了高精度的台站和复测点的矢量数据,基于此建立的三维模型,比国际地磁参考场IGRF12模型的精度更高.
(2) 本文用到的三维Taylor多项式模型为完整展开形式,其系数约为相同截断阶数下的经典二维展开模型的2N倍,因此三维模型在较低的截断阶数下反映出更多的地磁场信息,从而提高模拟效率.另外需要注意的是由于系数数量随截断阶数的增加呈现指数式上升,三维模型也较易出现龙格现象.文中当截断阶数N>5时,出现了明显的龙格现象.因此区域磁场建模时,截断阶数的选取和边界效应的控制是两个关键性问题(徐文耀和朱岗昆,1984;Feng et al.,2015),在确定模型的截断阶数时,除了考虑模型拟和精度外,还需要避免龙格现象的出现.
(3) 本文研究表明较低截数的三维模型,其均方偏差RMS与较高阶数的二维模型接近,通过对比两种模型在不同截断阶数下的RMS、磁场分布以及残差,可基本确定三维模型所对应的二维模型的阶数.
考虑到福建及邻近地区的测点特别密集且总体分布均匀,非常适于进行局部磁异常的研究.磁异常空间结构复杂,但在时间上却非常稳定,除非有重大的火山、地震等地质活动发生,磁异常变化的时间尺度往往以地质年代衡量(徐文耀等,2008).因此本文采用1960.0年的地磁实测数据进行研究是非常有意义的.通过比较可以发现,福建及邻近地区基于三维模型的H、D与I分量的分布和IGRF12、CM4(Sabaka et al.,2004;Olsen et al.,2010)全球模型的分布基本一致,但仔细观察会发现三维模型的H分量在福建和广东交界处存在一定的弯曲现象,强度变化不大.由于该区域具有较多的实测点,说明在该处地表(岩石圈层)或许存在微弱的磁异常.磁异常的研究具有重要的理论意义和实用价值,磁异常往往与磁性矿物的分布有关,因此磁异常测量是一种重要的找矿手段;磁异常分布还可能与地质活动有关,如火山活动时的热退磁效应引起的磁场快速变化,地震孕育或发生时由于压磁效应、热磁效应等原因引起的磁场变化等.因此,福建和广东交界处存在的弯曲现象可能是值得深入探讨的一个问题.
本研究基于区域实测点数据应用三维Taylor模型,取得了较为理想的拟合效果.在以后的相关研究中,可进一步与基于全球模型得到的区域模拟结果(康国发等,2010,2011)相比较验证;还可以结合全球磁场模型研究该区域的地壳磁异常场,发掘其可能潜在的经济价值.若能够结合CHAMP、SWARM等卫星数据,发展区域建模新方法(徐文耀等,2011),建立空间三维磁场模型,空间高度范围可实现从地面到卫星高度全覆盖,这对于研究电离层、磁层磁场空间物理机制和时空变化都有一定的借鉴意义.
致谢感谢审稿专家对本文提出的宝贵建议,感谢编辑部的支持和帮助.
References
Alldredge L R. 1982. Geomagnetic local and regional harmonic analyses.J.Geophys.Res.,87(B3): 1921-1926.
An Z C, Xu Y F. 1981. Methods of computation of geomagnetic field at greater altitude in a local region.Chin.J.SpaceSci.(in Chinese), 1(1): 68-73.
An Z C, Xu Y F, Wang Y H. 1991a. Derivation and analysis of the main geomagnetic field models in China for 1950—1980.ChineseJ.Geophys.(in Chinese), 34(5): 585-593.
An Z C, Wang Y H, Xu Y F. 1991b. Calculations and analyses of vertical gradient of the geomagnetic field in China and adjacent areas.Chin.J.SpaceSci.(in Chinese), 11(1): 14-23.
An Z C. 2000. Studies on geomagnetic field models of Qinghai-Xizang plateau.ChineseJ.Geophys.(in Chinese), 43(3): 339-345, doi:10.3321/j.issn:0001-5733.2000.03.007.
An Z C. 2001. Analyses and discussions of the geomagnetic field polynomial models.ChineseJ.Geophys.(in Chinese), 44(S): 45-50, doi:10.3321/j.issn:0001-5733.2001.z1.007.
Chen B, Gu Z W, Gao J T, et al. 2011. Analyses of geomagnetic field and its secular variation over China for 2005.0 epoch using Spherical Cap Harmonic method.ChineseJ.Geophys. (in Chinese), 54(3): 771-779, doi:10.3969/j.issn.0001-5733.2011.03.017. Düzgit Z, Baydemir N, Malin S R C. 1997. Rectangular polynomial analysis of the regional geomagnetic field.Geophys.J.Int.,128(3): 737-743.
Feng Y, Sun H, Mao F, et al. 2013a. Study on crustal magnetic anomaly over Mexico and its adjacent areas.ProgressinGeophysics(in Chinese), 28(3): 1355-1364, doi:10.6038/pg20130329.
Feng Y, Sun H, Jiang Y, et al. 2013b. Variation of the main magnetic field in Chinese mainland during 20th century.ActaSeismologicaSinica(in Chinese), 35(6): 865-875.
Feng Y, Jiang Y, Sun H, et al. 2013c. Calculation and analysis of geomagnetic field horizontal gradients and high altitude geomagnetic field.ProgressinGeophys. (in Chinese), 28(2): 735-746, doi:10.6038/pg20130222.
Feng Y, Sun H, Jiang Y. 2015. Data fitting and modeling of regional geomagnetic field.AppliedGeophysics, 12(3): 303-316.
Gao J T, An Z C, Gu Z W, et al. 2005. Selection of the geomagnetic normal field and calculation of the geomagnetic anomalous field.ChineseJ.Geophys. (in Chinese), 48(1): 56-62. Haines G V. 1985. Spherical cap harmonic analysis of geomagnetic secular variation over Canada 1960—1983.J.Geophys.Res.,90(B14): 12563-12574.
Jiang Y, Jiang Y, Feng Y, et al. 2015. Regional geomagnetic modelling based on the magnetic data of CHAMP satellite and 3D Taylor polynomial.ChineseJ.Geophys. (in Chinese), 58(9): 3121-3132, doi:10.6038/cjg20150909.
Kang G F, Gao G M, Bai C H, et al. 2010. Distribution of the magnetic anomaly for the CHAMP satellite in China and adjacent areas.ChineseJ.Geophys. (in Chinese), 53(4): 895-903, doi:10.3969/j.issn.0001-5733.2010.04.014.
Kang G F, Gao G M, Bai C H, et al. 2012. Characteristics of the crustal magnetic anomaly and regional tectonics in the Qinghai-Tibet Plateau and the adjacent areas.Sci.ChinaEarthSci.,55(6): 1028-1036.
Li Y S, Huang Y Q. 1978. Numerical Approximation (in Chinese). Beijing: People′s Education Press.
Liu S J, Zhou X G, Sun H, et al. 2011. The three dimension Taylor polynomial method for the calculation of regional geomagnetic field model.ProgressinGeophysics(in Chinese), 26(4): 1165-1174, doi:10.3969/j.issn.1004-2903.2011.04.005.
Olsen N, Mandea M, Sabaka T J, et al. 2010. The CHAOS-3 geomagnetic field model and candidates for the 11th generation IGRF.Earth,PlanetsSpace, 62(10): 719-727.
Ou J M, Du A M, Xu W Y, et al. 2012. The Legendre polynomials modeling method of small-scale geomagnetic fields.ChineseJ.Geophys. (in Chinese), 55(8): 2669-2675, doi:10.6038/j.issn.0001-5733.2012.08.019.
Qiao Y K, Wang S C, Zhang J S. 2008. Research on Taylor polynomial fitting in modeling of regional geomagnetic field.ChineseJournalofEngineeringGeophysics(in Chinese), 5(3): 294-298.
Sabaka T J, Olsen N, Purucker M E. 2004. Extending comprehensive models of the Earth′s magnetic field with Ørsted and CHAMP data.Geophys.J.Int.,159(2): 521-547.
Thébault E, Schott J J, Mandea M, et al. 2004. A new proposal for spherical cap harmonic modelling.Geophys.J.Int.,159(1): 83-103.
Thébault E, Schott J J, Mandea M. 2006. Revised spherical cap harmonic analysis (R-SCHA): Validation and properties.J.Geophys.Res.,111(B1): B01102.
Thébault E, Gaya-Piqué L. 2008. Applied comparisons between SCHA and R-SCHA regional modeling techniques.Geochem.Geophys.Geosyst.,9(7): Q07005.
Thébault E. 2008. A proposal for regional modelling at the Earth′s surface, R-SCHA2D.Geophys.J.Int.,174(1): 118-134.
Xu W Y, Zhu G K. 1984. A study of the RHA for the geomagnetic field of China and neighbouring region.ChineseJ.Geophys. (in Chinese), 27(6): 511-522.
Xu W Y, Zhu G K. 1985. Three dimentional structure of geomagnetic field in China and its secular variations.ChineseJ.Geophys. (in Chinese), 28(4): 356-363.
Xu W Y, Wei Z G, Xia G H. 2005. Regional features of the secular variation of the geomagnetic field in China for 2000.ChineseJ.Geophys. (in Chinese), 48(3): 551-560, doi:10.3321/j.issn:0001-5733.2005.03.012.
Xu W Y, Bai C H, Kang G F. 2008. Global models of the Earth's crust magnetic anomalies.ProgressinGeophys. (in Chinese), 23(3): 641-651.
Xu W Y, Ou J M, Du A M. 2011. An Analysis of errors in geomagnetic field models.ProgressinGeophys. (in Chinese), 26(5): 1485-1509, doi:10.3969/j.issn.1004-2903.2011.05.001.
Xu Y F, Wang Y H, An Z C. 1992. An analysis and the models of the geomagnetic secular variation in China for 1950—1985.ChineseJ.Geophys. (in Chinese), 35(6): 740-747.
Yang Y T, Shi Z Y, Guan Z Z, et al. 2009. A method of improving regional geomagnetic field model boundary effect.ProgressinGeophys. (in Chinese), 24(2): 468-474, doi:10.3969/j.issn.1004-2903.2009.02.013.
附中文参考文献
安振昌, 徐元芳. 1981. 局部地区高空磁场的计算方法. 空间科学学报, 1(1): 68-73.
安振昌, 徐元芳, 王月华. 1991a. 1950—1980年中国地区主磁场模型的建立及分析. 地球物理学报, 34(5): 585-593.
安振昌, 王月华, 徐元芳. 1991b. 中国及邻近地区地磁场垂直梯度的计算与研究. 空间科学学报, 11(1): 14-23.
安振昌. 2000. 青藏高原地磁场模型的研究. 地球物理学报, 43(3): 339-345, doi:10.3321/j.issn:0001-5733.2000.03.007.
安振昌. 2001. 地磁场多项式模型的分析与讨论. 地球物理学报, 44(增刊): 45-50, doi:10.3321/j.issn:0001-5733.2001.z1.007.
陈斌, 顾左文, 高金田等. 2011. 2005.0年代中国地区地磁场及其长期变化球冠谐和分析. 地球物理学报, 54(3): 771-779, doi:10.3969/j.issn.0001-5733.2011.03.017.
冯彦, 孙涵, 毛飞等. 2013a. 墨西哥及邻近地区地壳磁异常场研究. 地球物理学进展, 28(3): 1355-1364, doi:10.6038/pg20130329.
冯彦, 孙涵, 蒋勇等. 2013b. 20世纪中国地区主磁场变化研究. 地震学报, 35(6): 865-875.
冯彦, 蒋勇, 孙涵等. 2013c. 地磁场水平梯度及高空地磁场的计算与分析. 地球物理学进展, 28(2): 735-746, doi:10.6038/pg20130222.
高金田, 安振昌, 顾左文等. 2005. 地磁正常场的选取与地磁异常场的计算. 地球物理学报, 48(1): 56-62.
蒋勇, 姜乙, 冯彦等. 2015. 基于CHAMP卫星与三维Taylor多项式模型的区域地磁建模研究. 地球物理学报, 58(9): 3121-3132, doi:10.6038/cjg20150909.
康国发, 高国明, 白春华等. 2010. 中国及邻近地区CHAMP卫星磁异常的分布特征. 地球物理学报, 53(4): 895-903, doi:10.3969/j.issn.0001-5733.2010.04.014.
康国发, 高国明, 白春华等. 2011. 青藏高原及邻区的地壳磁异常特征与区域构造. 中国科学: 地球科学, 41(11): 1577-1585.
李岳生, 黄友谦. 1978. 数值逼近. 北京: 人民教育出版社.
柳士俊, 周小刚, 孙涵等. 2011. 用于区域地磁场模型计算的三维Taylor多项式方法. 地球物理学进展, 26(4): 1165-1174, doi:10.3969/j.issn.1004-2903.2011.04.005.
区家明, 杜爱民, 徐文耀等. 2012. 小尺度地磁场勒让德多项式建模方法. 地球物理学报, 55(8): 2669-2675, doi:10.6038/j.issn.0001-5733.2012.08.019.
乔玉坤, 王仕成, 张金生等. 2008. 泰勒多项式拟合法在区域地磁场建模中的应用研究. 工程地球物理学报, 5(3): 294-298.
徐文耀, 朱岗昆. 1984. 我国及邻近地区地磁场的矩谐分析. 地球物理学报, 27(6): 511-522.
徐文耀, 朱岗崑. 1985. 中国地磁场的三维结构及其长期变化. 地球物理学报, 28(4): 356-363.
徐文耀, 魏自刚, 夏国辉. 2005. 2000年中国地区地磁场长期变化的区域特征. 地球物理学报, 48(3): 551-560, doi:10.3321/j.issn:0001-5733.2005.03.012.
徐文耀, 白春华, 康国发. 2008. 地壳磁异常的全球模型.地球物理学进展, 23(3): 641-651.
徐文耀, 区家明, 杜爱民. 2011. 地磁场模型误差分析中的几个问题. 地球物理学进展, 26(5): 1485-1509, doi:10.3969/j.issn.1004-2903.2011.05.001.
徐元芳, 王月华, 安振昌. 1992. 1950—1985年中国地磁长期变化的模型和分析. 地球物理学报, 35(6): 740-747.
杨云涛, 石志勇, 关贞珍等. 2009. 一种改善区域地磁场模型边界效应的方法. 地球物理学进展, 24(2): 468-474, doi:10.3969/j.issn.1004-2903.2009.02.013.
(本文编辑胡素芳)
基金项目中央级公益性科研院所基本科研业务专项(DQJB14C02),国家重大科学仪器设备开发专项项目(2014YQ100817)及国家自然科学基金(41504129)联合资助.
作者简介张素琴,女,1978年出生,硕士,高级工程师,主要从事地磁学基础理论研究及地磁台网管理工作.E-mail:13521519246@139.com
doi:10.6038/cjg20160602 中图分类号P631
收稿日期2015-11-02,2016-03-22收修定稿
Study of regional geomagnetic model of Fujian and adjacent areas based on 3D Taylor Polynomial model
ZHANG Su-Qin, FU Chang-Hua, ZHAO Xu-Dong
InstituteofGeophysics,ChinaEarthquakeAdministration,Beijing100081,China
AbstractBased on 256 measured geomagnetic vector data (Element D, I and H) in Fujian and adjacent areas, combined with the grid data of Global Land One-kilometer Base Elevation Project and the latest 12th International Geomagnetic Referenced Field (IGRF12) model, the regional geomagnetic model has been created by using three-dimensional (3D) Taylor Polynomial model. Through comparing the Root-Mean-Square error (RMS), geomagnetic distribution and residuals, two main conclusions are drawn: (1) Truncation degree N=2 of 3D Taylor model basically produce the same calculation result as truncation degree N=6 of 2D Taylor model; (2) 3D Taylor model can calculate conveniently and has high precision, but it also has the probability of producing Runge Phenomenon. So, both calculation precision and boundary effect problem should be considered when determining truncation degree.KeywordsGeomagnetic model; 3D Taylor polynomial model; Fujian and adjacent areas; Root-Mean-Square error
张素琴,付长华,赵旭东. 2016. 基于三维Taylor模型的福建及邻近地区地磁模型研究. 地球物理学报,59(6):1948-1956,doi:10.6038/cjg20160602.
Zhang S Q, Fu C H, Zhao X D. 2016. Study of regional geomagnetic model of Fujian and adjacent areas based on 3D Taylor Polynomial model.ChineseJ.Geophys. (in Chinese),59(6):1948-1956,doi:10.6038/cjg20160602.

