核幔边界反射震相ScS对远震体波反演震源参数精度影响

钱韵衣， 倪四道

1 中国科学技术大学地球和空间科学学院， 合肥　230026　2 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室， 武汉　430077



核幔边界反射震相ScS对远震体波反演震源参数精度影响

钱韵衣1， 倪四道2*

1 中国科学技术大学地球和空间科学学院， 合肥2300262 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室， 武汉430077

摘要研究表明，远震直达体波波形(P波、SH波)是有效反演中强地震(M5.5～7)震源参数的重要资料.但是当震中距较大时，核幔边界全反射波ScS会进入SH波反演窗口，其未被传统的基于体波震源参数反演算法所考虑，从而导致反演结果偏差.本文通过TEL3与fk方法合成理论地震图，使用Jackknifing统计方法定量测试了不同情况下ScS震相对远震体波反演的影响.结果表明，当反演数据震中距位于70°～90°时，ScS震相会造成震源质心深度1 km左右、机制解最大8°的系统偏差；使用震中距40°～90°的SH波进行抽样反演，机制解最大系统偏差可达5°；SH波与P波联合反演可减少ScS震相引起的震源参数结果系统偏差.因此，ScS震相对基于射线理论的远震体波震源机制解反演所造成的误差是需要给予考虑的.

关键词远震体波； 震源深度； 震源机制解； 核幔边界； ScS震相

1引言

准确的机制解、深度等震源参数不仅对于研究地壳流变性质、岩石应力状态、区域地质构造、孕震机理等问题具有重要价值(许忠淮等，1989；石耀霖和朱守彪，2003；陈运泰和许力生，2003；吴建平等，2004)，其更是地震破裂过程研究的重要基础(王卫民等，2008；张勇等，2008；何骁慧等，2015).另外，准确的震源参数对于基于波形反演地球内部结构的工作也至关重要(Montelli et al.，2004)，例如，Chen等(2015a)利用地震波形对东亚地壳、地幔结构进行成像时，重新测定了地震质心位置及震源机制解等参数.由于小地震能量比较弱，其波形信噪比低，不利于获取质心深度、机制解等震源参数；而大地震数量少，其破裂过程比较复杂，难以仅用点源准确描述；因此，中等强度地震的震源深度与震源机制解在区域构造研究中得到广泛应用(e.g.Wright etal.，1999； Berberian et al.，2001； Biggs et al.，2006).

针对中强地震震源参数的测定方法已开展了大量研究，如基于体波到时(e.g. Spence，1980)、深度震相(e.g. Ma，2010；崇加军等，2010)与面波振幅谱(e.g. Fox et al.，2012)等信息进行深度测定的方法，以及利用P波初动(e.g. Hardebeck and Shearer，2002)、体波振幅或振幅比(e.g.Hardebeck and Shearer，2003)、近场全波形(e.g.Dreger and Helmberger，1993)、近场体波及面波(e.g.Zhao and Helmberger，1994)、长周期面波波形(e.g. Dziewonski et al.，1981)、远场体波波形(e.g.Sipkin，1982)与W震相(e.g. Kanamori and Rivera，2008)等资料进行震源机制解反演的方法.其中，远震直达体波数据是反演中强地震震源参数的重要资料；因此，中外学者发展了一系列的基于远震体波确定中强地震(M5.5～7)震源参数的反演方法及软件，例如MT5程序(Zwick et al.，1994)和CAPtel软件包(Chen et al.，2015b).这些远震体波反演方法都基于射线理论计算格林函数，与基于波数频率、有限差分、有限元等全波形格林函数计算方法相比，具有快速的特点.上述震源机制解反演方法在地震研究中得到了广泛应用，得到的震源参数较为一致，但是统计表明其仍存在15°左右偏差(Frohlich and Davis，1999)，这往往难以满足区域地质构造精细研究需求.例如，Zhan等人(2012)进行了远震直达体波震源参数反演，发现了2011年Tohoku-Oki地震区域MW5.5～7.5中强前震及余震存在5°～10°的倾角变化，并据此提出了该俯冲带区域可能的三种地质构造模型.因此，有必要分析造成机制解15°偏差的具体原因，并提出相对应的解决方案以提高震源参数反演精度.

震源点源近似假设、台站分布不均匀、反演方法系统误差等因素都可能会导致震源参数的偏差.而目前的多数体波反演采用了基于射线理论的格林函数计算方法，合成理论地震图中只包括了P波、SH波、PP等地幔转折波(turning wave)，很少考虑到地核的影响，未能包含ScS、PcP等震相，有可能导致震源参数反演结果偏差.由于地球外核是液态，剪切波不能传播，因此地幔中的SH波可被核幔边界(Core Mantle Boundary，简称CMB)完全反射，形成的ScS震相一般比较清晰.例如，在合成地震图中(图1)可以观测到明显的ScS震相，其幅度与SH波可比；而且随着震中距的增大，ScS与直达SH波的到时差逐渐减小，当两者到时差小于反演窗口长度时，在震源参数反演中SH波将受到ScS震相的影响.因此，需要定量研究该震相对震源参数反演的影响.

本文基于一维层状模型，通过TEL3及fk正演方法计算合成远震体波波形，作为输入数据，测试ScS震相对中等强度地震质心深度、机制解等震源参数的影响.其中，基于几何射线理论的TEL3(Telesiesmic body-wave in 3-componet)程序是CAPtel方法快速计算体波理论格林函数的工具，而采用频率-波数域双重积分的fk(frequency-wavenumber)方法能够计算全波形理论地震图(图1b).测试时将不包含ScS震相的格林函数(TEL3或fk计算)分别作为正演所需的数据库，使用包含ScS震相的波形(fk计算)作为输入数据，将其输入CAPtel程序，进行仅使用SH波的单独反演以及SH+P波的联合反演.最后，本文还对射线理论计算SH波不准确性造成的影响及D″层剪切波速度异常下ScS对震源参数精度的影响等因素进行了讨论.

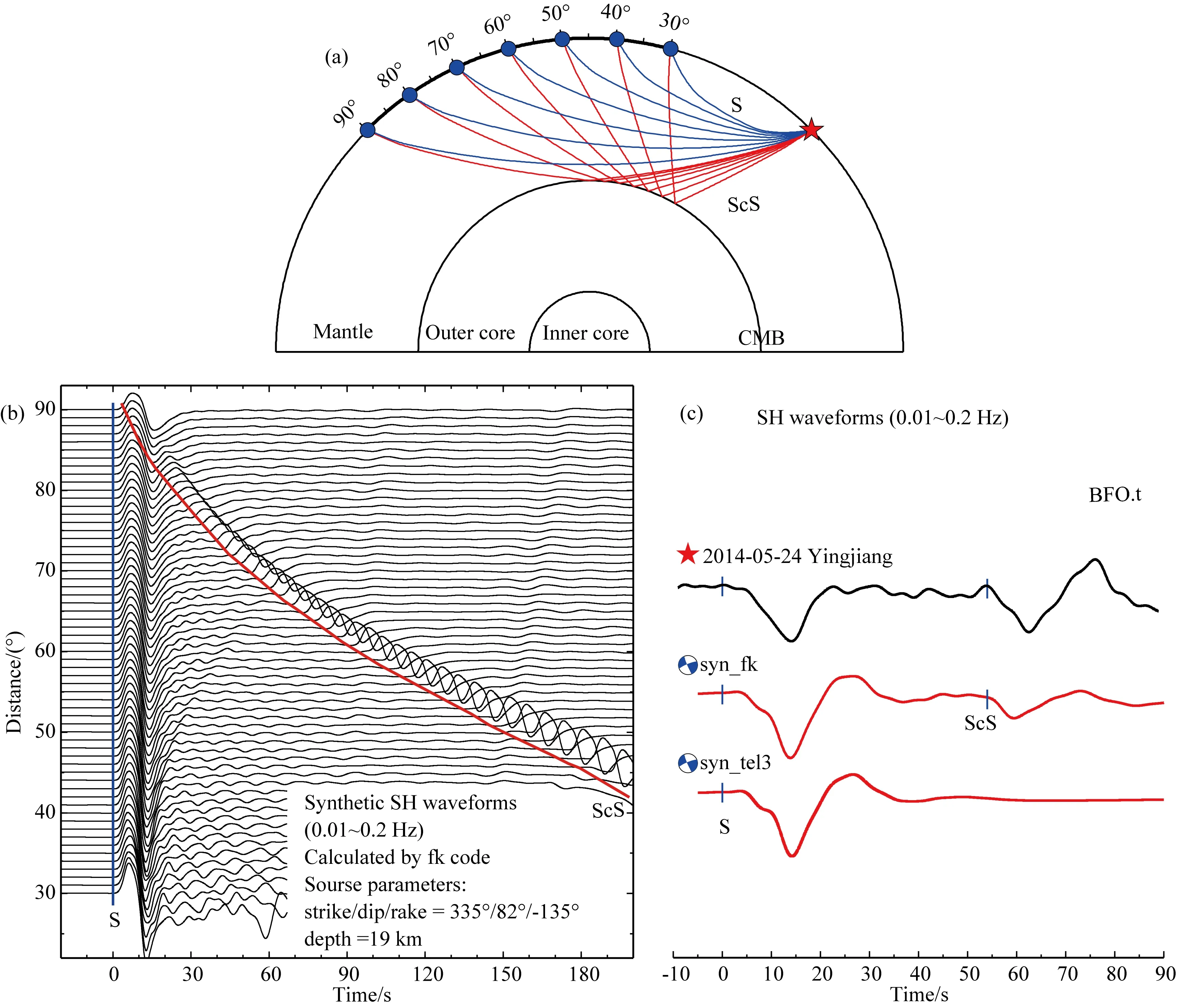
图1　S波与核幔边界反射震相ScS波(a) 射线路径示意图，蓝线为S波射线路径，红线为ScS传播路径； (b) T(切向)分量合成地震图，蓝色为直达S波，红色为ScS震相； (c) 2014年5月24日5.7级盈江地震在BFO台站上的SH波形图，黑色为实际数据，红色分别为由fk、TEL3合成的理论波形(震源参数使用CAPtel反演结果：深度9 km、走向248°、倾角80°、滑动角6°).Fig.1　The direct S wave and the core-refleted wave ScS(a) Ray paths for direct S wave (blue) and the ScS phase (red)； (b) Synthetic waveforms for S wave and ScS in tangential component； (c) The observed (black) and synthetic (red) SH waveforms of MW5.7 Yingjiang earthquake in BFO station. The black line is observed waveform. The red lines are synthetic waveforms calculated by fk and TEL3，while the source parameters provided by CAPtel are 9 km、248°、80°、6°.

2方法

由于实际地震波在传播过程中会受到真实地球三维结构的改造，且通常情况下发震断层的质心深度及机制解等参数很难精确知道，这些因素都不利于定量研究核幔边界反射波ScS对震源参数反演结果造成的偏差.因此，文本使用全波形理论地震图作为输入数据，定量研究ScS震相对远震体波震源参数反演精度的影响.目前，计算全波形理论地震图的方法主要有基于傅里叶变换利用传播矩阵(Haskell，1953)或广义反射透射系数矩阵(Luco and Apsel，1983)计算层状介质的积分变换方法、将波动方程直接离散化的有限差分法(Virieux，1986)、谱元法(Komatitsch and Tromp，2002)等数值方法以及本征模合成法(Gilbert and Dziewonski，1975)等.其中，采用有限差分等数值方法进行大尺度或高频地震波模拟时，需要高性能计算设备；而本征模合成方法在实际应用中主要用于计算地球自由震荡和面波的理论地震图，对于短周期体波的计算成本非常高(谢小碧等，1992).本文采用在频率域对全频率段数据进行计算叠加的积分变换方法计算横向均匀分层模型中的远震全波形理论地震图，该方法能够计算地球模型中产生的所有反射、透射震相.目前，比较常用的计算工具有采用广义反射透射系数矩阵连接层间参数的grtm程序(Chen and Zhang，2001)、利用传播矩阵进行计算的qseis(Wang，1999)及fk程序(Zhu and Rivera，2002)等.其中，已实现并行化的fk程序稳定可靠、可大幅度提高运算速度(韩立波等，2007)，因此本文使用fk并行化版本计算远震全波形理论地震图.

当使用全波形理论地震图作为输入数据时，利用其体波部分反演地震震源参数的关键在于快速计算正演体波波形.Helmberger(1974)推导了基于拉普拉斯变换计算直立断层剪切位错源的远场体波表达式.Langston和Helmberger(1975)又将该公式推广，使计算横向均匀分层模型中任意位错点源的P、SV、SH波波形成为了可能.在此基础上，发展了许多基于射线理论快速合成远震体波波形的方法，如在时间域叠加卷积的TBW(Teleseismic Body-Wave)程序包(Kikuchi and Kanamori，1991)、采用反射系数进行计算的SYN系列软件包(McCaffrey et al.，1991)、使用射线理论与Haskell矩阵相结合的方法计算远震格林函数的TEL3程序(Chu et al.，2014)等.其中，TEL3方法基于Kikuchi和Kanamori的子程序软件包，能够快速计算水平分层介质中的格林函数，得到了成功的应用(e.g. Huang et al.，2012；谢祖军等，2013).因此，本文将该程序作为计算反演所需的体波格林函数的工具，测试ScS对震源参数反演可能造成的影响.本文使用了CAPtel程序进行反演.参考陈伟文等人(2012)的研究，反演窗长为60 s，对其滤波频带选用0.01～0.2 Hz.在CAPtel反演中P波、SH波的衰减因子t*值通常分别采用1 s、5 s(韦生吉，2009).

3ScS震相对反演精度的影响

3.1数据合成与处理

为了模拟真实台站分布情况，本文以2014年5月24日M5.7盈江地震为例，选用了全球地震台网(Global Seismographic Network，简称GSN)中记录到此次事件且震中距位于30°～90°的52个台站(简称GSN台站)(图2).参照其震中距及方位角信息使用fk方法计算远震波形作为输入数据，并使用CAPtel方法进行震源参数反演.

图2　震中及台站分布示意图五角星代表2014年5月24日盈江地震震中位置，三角形表示远震台站.Fig.2　Epicenter location and station distribution Star represents the epicenter of 20140524 Yingjiang earthquake， while triangle indicates teleseismic station.

由于分层地壳模型可导致P波及SH波多次波的产生，为了更突出地体现ScS对震源参数的影响，本文采用了去除地壳的PREM模型作为地球结构进行正演反演.为了直观地展示出射线理论格林函数的确没有包含ScS，在图3a中我们对比了盈江地震的fk合成地震图(黑色)与TEL3合成地震图(红色).在合成地震图过程中，采用了Global CMT提供的震源参数，质心深度为19 km，机制解为335°、82°、-175°，震源持续时间为3.6 s.可以看出，在70°～90°震中距范围内，fk合成地震图与TEL3合成地震图的SH波几乎相同，但是fk合成地震图中在SH波之后有明显的一个震相，推测为ScS.为了确认该震相确实是CMB反射造成的，我们采用fk方法计算了没有地核且底部为辐射边界条件时的合成地震图，简称为fk_noCMB(图3b红色)，相应地，包含地核的合成地震图称为fk_CMB(图3b黑色).由图3b可以看出，SH波完全一致，但是fk_noCMB中没有后续震相，因此fk_CMB中的后续震相确实是CMB反射造成的.图3a中，震中距为30°～40°时，fk与TEL3方法合成的SH波形存在一定的差异，这可能是由于射线理论未能很好处理地幔过渡区结构造成的，因此本文仅使用震中距40°～90°的45个台站参与反演测试.由图3可知，当反演窗长为60 s时，震中距大于70°的SH窗口中就会混入ScS震相.因此，下文中分别对70°～90°、40°～70°、40°～90°三个震中距范围进行测试.

3.2反演测试与分析

本文进行两组反演测试，通过反演得到的震源参数与输入参数的比较，定量地探讨ScS震相对反演震源参数精度的影响.第一组测试使用fk_CMB合成地震图作为输入数据，采用 TEL3格林函数进行反演，研究ScS震相对射线理论反演震源参数造成的偏差.由于射线理论计算得到的SH波只是对准确波形的近似，它们的偏差也有可能影响震源参数测定.因此，进行了第二组测试，采用fk_noCMB计算的格林函数进行反演，研究SH波准确计算情况下ScS震相对震源参数反演造成的影响.

第一组测试了不同震源机制解情况下ScS造成的影响.首先计算各种典型机制解(逆冲、走滑、倾滑等)下的远震全波形地震图(fk_CMB)，并作为输入数据使用CAPtel程序进行反演.对于斜滑型地震，当输入震源质心深度为19 km、走向335°、倾角82°、滑动角-135°时，使用震中距70°～90°的16个波形记录反演得到的最佳震源参数为质心深度19 km、节面Ⅰ断层面解为334°、83°、-137°(见图4)，反演得到的结果与输入的震源机制解存在-1°、1°、-2°的差异.考虑不同震中距范围台站数目及其分布可能会影响测试结果，本文使用Jackknifing方法(Tichelaar and Ruff，1989)对不同震中距数据进行重采样，系统地评估反演结果与输入参数之间的偏差.统计结果显示，当随机使用大于5个台站进行CAPtel反演时，得到的震源参数就比较可靠(Wei et al., 2012).因此，依次对震中距70°～90°的16个、40°～70°的29个、40°～90°的45个GSN台站数据进行抽样测试时，为了保证抽样台站分布均匀，限定每个方位角象限随机抽样2个不同台站，每次重抽样样本数为8个台站.分别对采样次数为100、200、300、400的情况进行测试发现：当抽样总数为100时，统计结果不稳定；抽样次数为200时，概率最大的统计值趋于稳定；抽样总数为300与400时，两者统计结果稳定且较为一致.因此，本文中Jackknifing采样次数均选用300次.图5显示了震中距70°～90°SH波波形抽样反演系统偏差结果，柱状图中红色圆点指示百分比最高的偏差值，即震源参数系统误差；蓝色线段为反演偏差可能覆盖的范围.结果显示，深度、走向、倾角、滑动角系统偏差分别为0 km、-1°、2°、-2°.

图3　远震理论SH波波形对比(a) 黑色为fk_CMB合成地震图，红色为TEL3合成地震图； (b) 黑色为fk_CMB合成地震图，红色为fk_noCMB合成地震图.合成地震图的震源参数选用Global CMT提供2014年5月24日盈江地震的参数，震中距及方位角采用GSN台站分布，滤波范围为0.01～0.2 Hz.Fig.3　The comparison of different teleseismic synthetic SH waveforms(a) The black lines are fk_CMB synthetic waveforms and the red lines are TEL3 synthetic waveforms； (b) The black lines are fk_CMB synthetic waveforms and the red lines are fk_noCMB synthetic waveforms. The source parameters of 20140524 Yingjiang earthquake are provided by Global CMT，while epicentral distance and azimuth of stations are given by GSN. Waveforms are all filtered between 0.01 to 0.2 Hz.

图4　震中距70°～90°SH波波形CAPtel反演结果(a) SH波位移记录波形拟合图(0.01～0.2 Hz)；黑色为fk_CMB合成波形，红色为TEL3格林函数反演波形；波形左上方为台站名，下方为波形拟合互相关系数(%)，右下方两个数字分别代表震中距(°)与方位角(°)； (b) 输入参数及反演结果示意图，红色三角图标为震中距70°～90°台站在震源球下半球的投影， 震源球旁边为两个最佳节面的机制解(走向、倾角、滑动角)； (c) 反演误差随深度变化图， 黑色震源球所在深度为反演的最佳深度.Fig.4　A CAPtel inversion using SH waveforms in the epicentral distance range 70°～90°(a) Waveform modeling for SH displacement records at 0.01～0.2 Hz. The black lines show fk_CMB synthetic waveforms，while the red lines show TEL3 synthetic waveforms. The station name is labeled on the upper left of each figure and numbers under the seismograms are cross-correlation coefficient in percent(left) , epicentral distance and azimuth in degree(right). (b) The input and inverted parameters. Sampling of teleseismic body wavesin the epicentral distance range 70°～90° (red triangles) on the lower hemisphere of a dip-oblique-slip focal mechanism. (c) Inversion misfit of grid-searched focal depth.

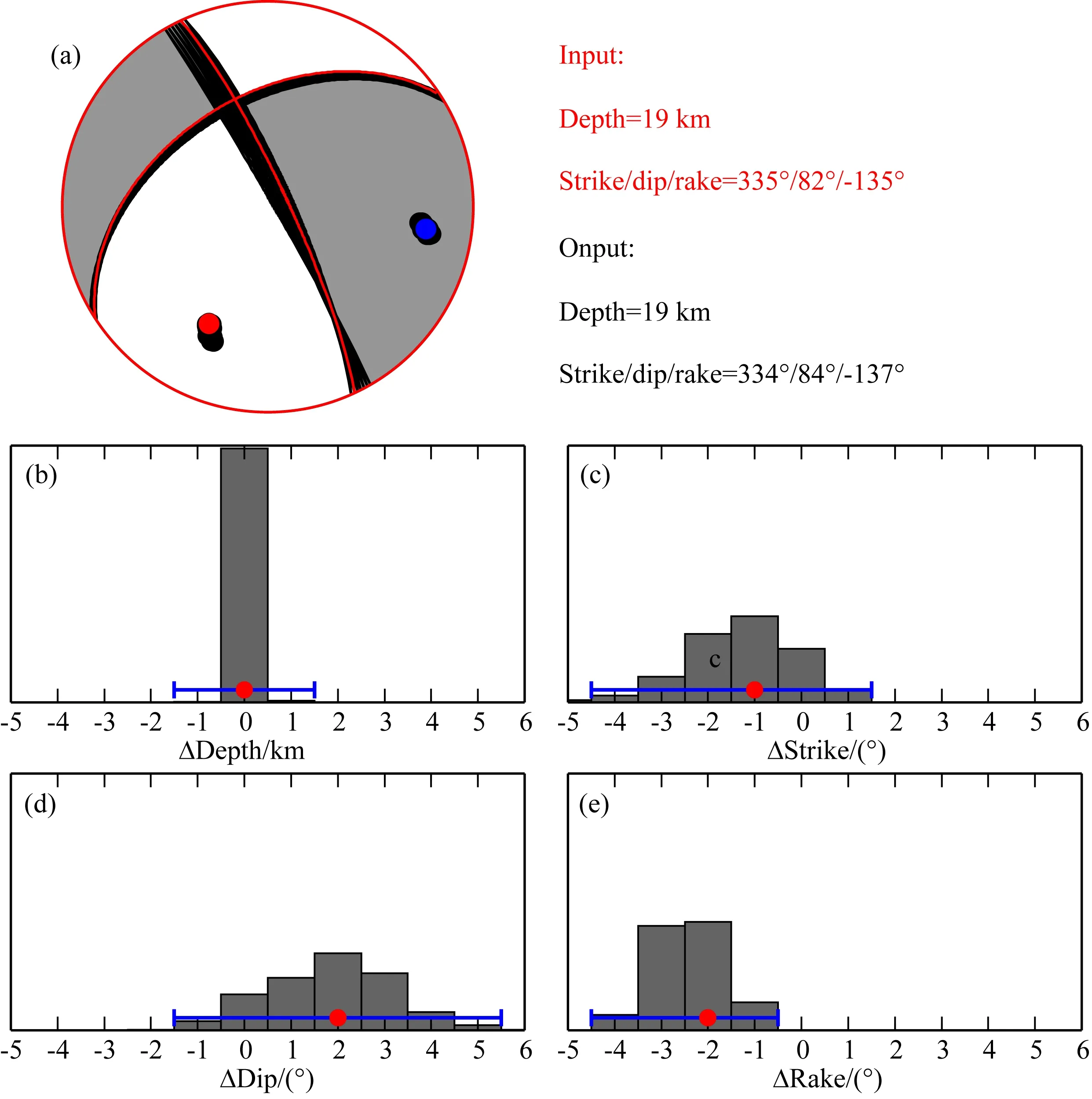
图5　震中距70°～90°SH波波形Jackknifing重抽样反演结果(a) 输入参数(红色)与反演最佳参数(黑色)示意图；红色震源球及大圆点采用输入机制解信息，黑色震源球及小圆点为300次重抽样反演结果的叠加；红色和蓝色圆点分别表示P轴、T轴； (b—e) 分别为深度、走向、倾角、滑动角等震源参数的反演偏差直方图，红色圆点为系统偏差，蓝色线段为反演偏差覆盖范围.Fig.5　The statistical results using SH waveforms in the epicentral distance range 70°～90°(a) The input (red) and best inverted (black) parameters. Red beachball and big dots show the input focal mechnism，while the black beachballs and small dots show the Jackknifing results. Red and blue dots indicate the P axes and T axes. (b—e) display the histograms of depth, strike, dip, rake of the Jackknifing results, respectively. Red dots show systematic deviations and blue lines cover the maximum deviations.

将不同震源机制解波形数据的系统偏差结果汇总，如表1所示.对于震源质心深度19 km的45°倾角逆冲(正断)和近直立走滑型地震，ScS震相对其震源参数反演结果没有明显影响；而对于近直立倾滑型等其他机制解类型的地震，ScS震相对于震中距70°～90°及40°～90°的数据机制解反演结果可造成一定的系统偏差.通过对比发现，ScS震相对近直立斜滑地震影响相对较大，输入震源机制解为335°、82°、-135°时，震中距70°～90°数据的走向、倾角、滑动角分别会产生-1°、2°、-2°的系统偏差，震中距40°～90°数据的质心深度、走向、倾角、滑动角也有1 km、-1°、3°、-2°的系统差异.值得注意的是，滑动角为45°的统计结果与其为-135°时的值完全一致，这是由于当其他参数一致、仅滑动相差180°时，两者合成的波形恰好为正负相反的关系，即可认为ScS震相对SH波波形干扰的贡献是相同的.通过分析表1中仅滑动角相差180°的机制解反演统计结果，发现它们统计规律几乎完全一致，这也可验证本文重抽样结果是可靠的.而震中距40°～70°的反演，机制解几乎没有系统偏差(±1°之内)，而此时ScS震相在反演窗口之外.这从侧面表明，本组测试中震中距70°～90°时的系统偏差主要是ScS造成的.

第二组测试中，使用了第一组中的SH波形作为原始数据，采用fk_noCMB的格林函数进行反演.首先参照表1中内容进行测试，结果如图6所示.可以看出，震中距70°～90°波形数据反演结果出现了不同程度的系统偏差；而震中距40°～70°抽样结果显示系统偏差都为0(km或°)，其可能出现的最大偏差值也较小；在震中距40°～90°反演中，由于仅部分震中距数据受ScS震相影响，只有滑动角有-1°的系统偏差.接着，本文对震源深度9～29 km每5 km为间隔的5个斜滑型地震(335°、82°、-135°)进行抽样测试.图7为震中距70°～90°数据远震SH波震源参数反演精度偏差分布图，可以看出，对于机制解相同、深度不同的5个斜滑型地震，统计得到的反演结果系统偏差比较一致.由此可见，ScS波对浅源地震(<30 km)震源参数反演精度造成的系统偏差几乎不随地震深度的改变而变化.

表1　不同机制解类型的SH波反演结果偏差值(输入数据为fk_CMB合成地震图，正演格林函数由TEL3计算)

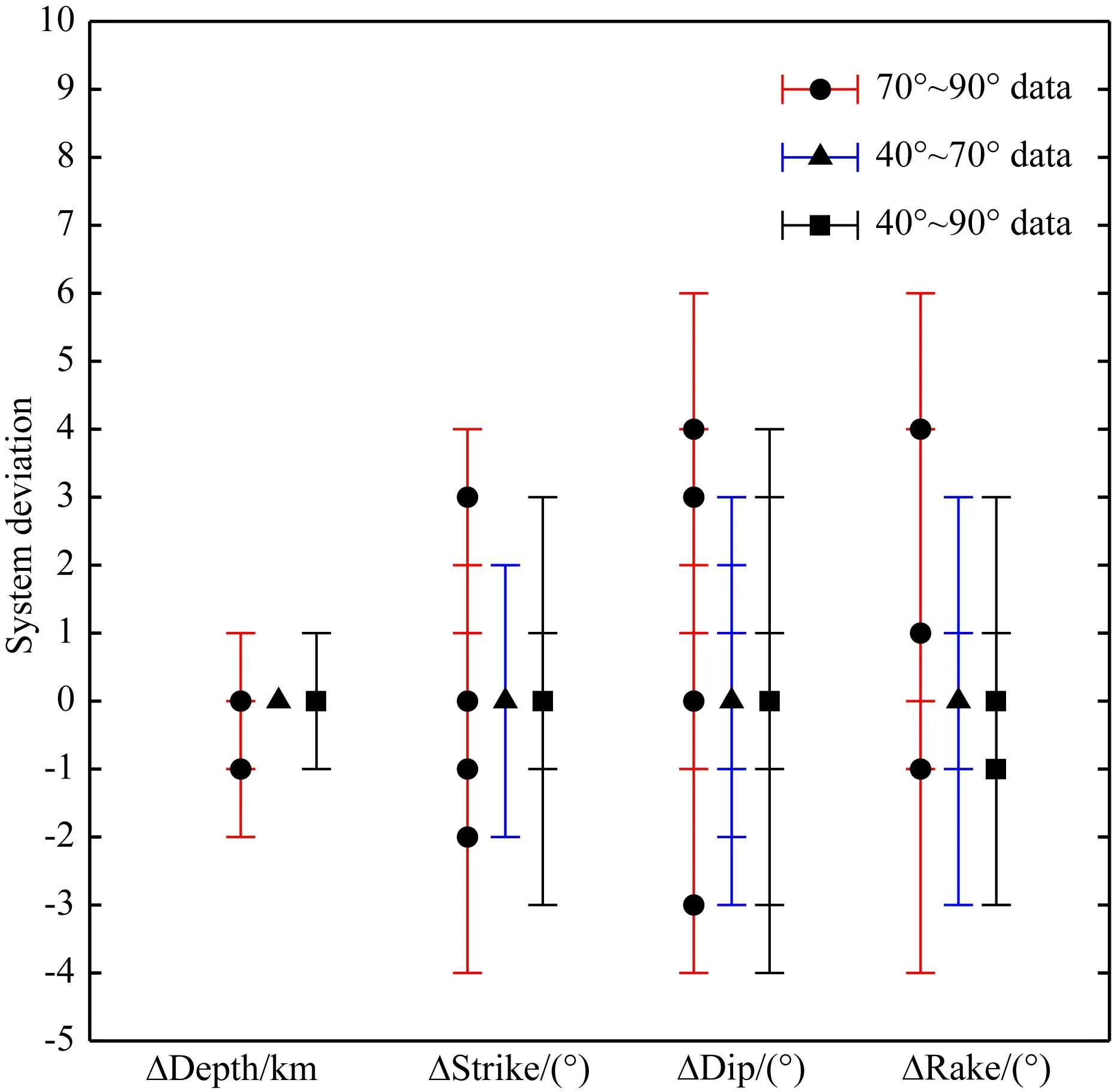
图6　不同震中距范围的SH波重抽样反演偏差结果采用fk_CMB合成地震图作为输入数据(输入震源参数参照表1)，fk_noCMB格林函数进行反演.黑色圆形、三角形及方块图标分别为震中距70°～90°、40°～70°、40°～90°数据Jackknifing系统偏差值，不同颜色的线段分别表示其反演偏差可达范围.Fig.6　Deviations of different epicentral distance ranges in SH wave inversions Using fk_CMB synthetic seismograms as the input data (The type of focal mechanism and the input source parameters are same in Table 1)，while using fk_noCMB green′s function waveforms to invert the best fit solution of depth, strike, dip and rake in CAPtel. Circle, triangle and diamond respectively represent systematic deviations of epicentral distance ranges in 70°～90°, 40°～70°, 40°～90° of Jackknifing results, while the red, blue and black lines show the relevant maximum deviations.

4讨论

以上两组测试讨论了ScS造成的影响，还须分析射线理论计算SH波不准确性造成的影响.使用fk_noCMB合成地震图作为输入记录，采用TEL3计算的格林函数进行抽样反演.由图8与图4、5对比可知，当输入波形不包含ScS震相时，震中距70°～90°SH波波形拟合互相关系数明显提高，都达到98%以上；且震源参数反演系统偏差也相应减少，分别为0 km、0°、0°、-1°.对不同机制解类型数据的抽样结果也表明，当无ScS震相干扰时，使用震中距70°～90°的数据进行反演仅能引起机制解±1°的系统偏差，这与震中距40°～70°数据(不受ScS影响)统计结果一致.此测试中机制解系统偏差是由于两种方法计算的直达SH波的差异造成的，由此表明，射线理论计算SH波的不准确性会造成机制解1°左右的系统偏差.

图7　不同地震深度时的70°～90°SH波震源参数反演系统偏差结果采用fk_CMB合成地震图作为输入数据(震源机制解为335°、82°、-135°)，使用fk_noCMB格林函数进行反演.五角星、菱形、方块与三角形分别代表深度、走向、倾角及滑动角等震源参数的Jackknifing系统误差值.Fig.7　Deviations of different input focal depths in SH wave inversions Using fk_CMB synthetic seismograms as the input data (The parameters of focal mechanism are 335°、82°、-135°)，while using fk_noCMB green′s function waveforms to invert the best fit solution of depth, strike, dip and rake in CAPtel.Star, rhombu, diamond andtriangle respectively represent systematic deviations of depth, strike, dip and rake of Jackknifing results.

此外通过全球层析成像、射线走时残差及波形拟合等研究发现，CMB上部D″层存在着全球分布、剪切波速度异常的不均匀区域(Ritsema et al.，2011)，比如非洲下地幔底部就存在一个超低速区域，其在D″层的剪切波速度表现为负异常(Ni and Helmberger，2003).当D″层的剪切波速度结构存在异常时，CMB全反射震相ScS的到时将会提前或延后，其波形也会受到相应的改造(图9).对第一组测试中输入波形的地球一维模型进行修改，将CMB以上300 km层状区域分别添加±5%的剪切波速度异常，测试输入震源深度为19 km、机制解分别为335°、82°、-135°的斜滑型地震时，使用fk计算该异常模型下的SH波作为输入数据，依然使用第一组测试中TEL3合成的格林函数，测试反演参数与输入参数的系统偏差.如表2所示，当D″层存在±5%的S波速度异常时，震中距40°～70°数据的系统偏差会稍微偏大，且包含震中距大于70°波形数据的误差也更大.震中距70°～90°、40°～90°数据反演结果显示，当CMB顶部存在剪切波速度异常时，ScS震相对震源参数反演结果的影响较无剪切波速度异常时会更大，各参数的系统偏差绝对最大值可达8°.所以，在D″层存在剪切波速度(正或负)异常的PREM模型中ScS波对反演震源参数的影响并不会随着该震相的复杂而减小，相反地，其会与射线理论不准确性等效应产生的结果相互耦合，共同地影响震源参数的精度.

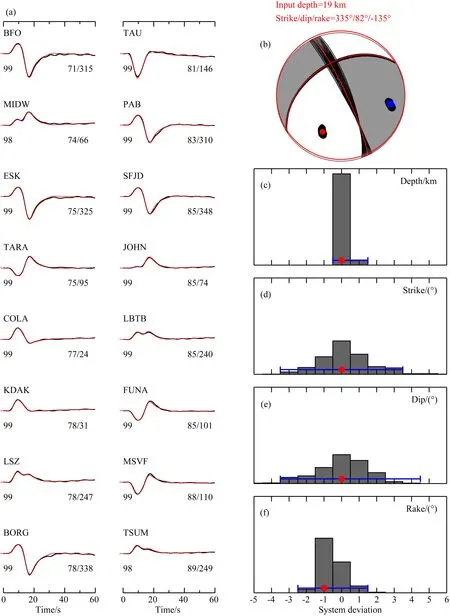
图8　震中距70°～90°SH波波形拟合及系统偏差结果(a) SH波位移记录波形拟合图(0.01～0.2 Hz)，黑色为fk_noCMB合成波形，红色为使用TEL3格林函数反演得到的合成地震图；波形左上方为台站名， 下方为波形拟合互相关系数(%)， 右下方两个数字分别代表震中距(°)与方位角(°)； (b) 输入参数与反演结果的震源球示意图； (c—f) 深度、走向、倾角、滑动角等震源参数系统偏差直方图.Fig.8　The waveform modeling and systematic deviations using SH waveforms in the epicentral distance range 70°～90°(a) Waveform modeling for SH displacement records at 0.01～0.2 Hz. The black lines show fk_CMB synthetic waveforms，while the red lines show fk_noCMB synthetic waveforms. The station name is labeled on the upper left of each figure and numbers under the seismograms are cross-correlation coefficient in percent (left), epicentral distance and azimuth in degree (right).(b) Red beachball and big dots show the input focal mechnism，while the black beachballs and small dots show the Jackknifing results. Red and blue dots indicate the P axes and T axes.(c—f)display the histograms of depth, strike, dip, rake of the Jackknifing results, respectively. Red dots show systematic deviations and blue lines cover the maximum deviations.

表2　D″层存在剪切波速度异常时SH波反演结果系统偏差结果(输入震源参数为19 km、335°、82°、-135°)

δVs震中距70°～90°震中距40°～70°震中距40°～90°深度/km走向/(°)倾角/(°)滑动角/(°)深度/km走向/(°)倾角/(°)滑动角/(°)深度/km走向/(°)倾角/(°)滑动角/(°)0%0-12-3001-11-13-2+5%1-6810-12-21-25-2-5%-148-10-12-21-35-2

研究表明，震源机制解测定的不准确度在±15°之内，其误差可能来源于简化震源运动模型假设、反演方法系统误差、台站分布以及真实地球结构的不均匀性等方面.本文使用一维地球模型下的理论全波形替代实际波形作为输入数据，通过重抽样方法保证每次反演的台站数量一致且分布均匀，发现CMB反射震相ScS是造成机制解偏差的重要原因之一.第二组测试中(图6)，使用震中距70°～90°SH波数据进行反演，仅由ScS震相造成了震源机制解系统偏差4°，最大偏差6°；使用震中距40°～90°SH波数据进行反演，系统偏差1°左右，最大误差仍可达3°.而且，实际远震体波震源机制解的测定采用了基于射线理论的格林函数进行反演，研究ScS震相对射线理论反演震源参数造成的系统偏差具有重要意义.第一组测试结果表明(表1)，ScS震相对射线理论反演震源机制解造成的系统偏差为4°左右，最大偏差6°.当D″层剪切波速度存在异常时(表2)，震中距70°～90°SH波数据反演机制解最大系统偏差为8°，其几乎占震源机制解总误差的二分之一；40°～90°波形数据的反演误差最大仍可达5°，为总误差的三分之一.由于ScS波波形随着震源机制解及台站方位角的变化而改变较大，而对震源质心深度的变化并不敏感，因此ScS波对远震体波反演中等地震震源机制解的精度影响较大，而对震源深度的测定结果影响较小.

与ScS震相相比，核幔边界反射波PcP的振幅较弱，其对P波波形的影响相对较小(Yu et al.，2012)；因此可以利用震中距40°～90°的P波与SH波联合反演，降低CMB全反射震相对反演结果的影响.使用震中距及台站分布均匀的45个震中距40°～90°台站的P波及SH波数据进行联合反演，可较好地压制核幔边界全反射震相ScS的干扰，将反演结果不准确度减少到±1°之内(如图9所示).

5结论

对于中等强度地震，较大震中距上ScS震相会干扰SH波的波形，如果基于射线理论计算的理论波形未包含核幔边界全反射震相，远震体波震源参数反演结果就会出现一定的偏差.本文将fk_CMB合成地震图中T(切向)分量波形作为原始数据，采用不包含ScS震相的格林函数在CAPtel中进行反演，根据Jackknifing重抽样方法测定了不同机制解类型地震的反演结果系统偏差，并证实了ScS震相是造成误差的主要原因.测试结果表明：震中距70°～90°数据反演质心深度系统偏差1 km左右、震源机制解系统偏差可达8°(表2).与前人研究发现的机制解偏差可达15°相比，ScS造成的影响是可观的.因此，ScS震相对基于射线理论的远震体波震源机制解反演所造成的误差需要给予考虑.

本文的工作是基于一维参考地球模型PREM开展的，选取了几种典型震源机制解及质心深度的中等强度地震进行研究，测试了当格林函数忽略ScS震相时所造成的反演精度偏差.然而，ScS造成的机制解偏差尚不足以解释前人发现的15°机制解偏差，震源附近三维结构造成的影响可能是更为重要的，本文的结论可能主要适用于横向结构变化不显著的震源地区.对于俯冲带、盆地边缘等结构复杂地区，还须综合考虑三维结构及核幔边界反射震相造成的影响.在实际远震体波波形反演中，由于三维结构的影响，不同震中距台站上的ScS震相的到时及形状会与其理论波形不一致，这可能会平均掉格林函数中忽略核幔边界反射震相引起的波形变化.因此，需要进一步开展三维模型下震源参数测定方面的系统工作，并发展三维情况下包含ScS波等后续震相的远震体波格林函数快速正演工具.

致谢感谢韩立波博士提供fk计算理论地震图并行版程序.本文中图件由GMT绘图软件完成.

References

Berberian M, Jackson J A, Fielding E, et al. 2001.The 1998 March 14 Fandoqa earthquake (Mw6.6) in Kerman province, southeast Iran: re-rupture of the 1981 Sirch earthquake fault, triggering of slip on adjacent thrusts and the active tectonics of the Gowk fault zone.GeophysicalJournalInternational, 146(2): 371-398.

Biggs J, Bergman E, Emmerson B, et al. 2006. Fault identification for buried strike-slip earthquakes using InSAR: The 1994 and 2004 Al Hoceima, Morocco earthquakes.GeophysicalJournalInternational, 166(3): 1347-1362.

Chen M, Niu F L, Liu Q Y, et al. 2015a. Multiparameter adjoint tomography of the crust and upper mantle beneath East Asia: 1. Model construction and comparisons.JournalofGeophysicalResearch:SolidEarth, 120(3): 1762-1786. Chen W W, Ni S D, Wang Z J, et al. 2012. Joint inversion with both local and teleseismic waveforms for source parameters of the 2010 Kaohsiung earthquake.ChineseJ.Geophys.(in Chinese), 55(7): 2319-2328, doi: 10.6038/j.issn.0001-5733.2012.07.017.

Chen W W, Ni S D, Kanamori H, et al. 2015b. CAPjoint, A computer software package for joint inversion of moderate earthquake source parameters with local and teleseismic waveforms.SeismologicalResearchLetters, 86(2A): 432-441.

Chen X F, Zhang H M. 2001.An efficient method for computing Green's functions for a layered half-space at large epicentral distances.BulletinoftheSeismologicalSocietyofAmerica, 91(4): 858-869.

Chen Y T, Xu L S. 2003.Tomography of the source process of large earthquakes in the Tibetan plateau and its surrounding region.EarthScienceFrontiers(in Chinese), 10(1): 57-62, doi: 10.3321/j.issn:1005-2321.2003.01.007.

Chong J J, Ni S D, Zeng X F. 2010. sPL, an effective seismic phase for determining focal depth at near distance.ChineseJ.Geophys.(in Chinese), 53(11): 2620-2630, doi: 10.3969/j.issn.0001-5733.2010.11.010.

Chu R S, Ni S D, Pitarka A, et al. 2014.Inversion of source parameters for moderate earthquakes using short-period teleseismic P waves.PureandAppliedGeophysics, 171(7): 1329-1341.

Dreger D S, Helmberger D V. 1993.Determination of source parameters at regional distances with three-component sparse network data.JournalofGeophysicalResearch:SolidEarth, 98(B5): 8107-8125.

Dziewonski A M, Chou T A, Woodhouse J H. 1981. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity.JournalofGeophysicalResearch:SolidEarth, 86(B4): 2825-2852.Fox B D, Selby N D, Heyburn R, et al. 2012. Shallow seismic source parameter determination using intermediate-period surface wave amplitude spectra.GeophysicalJournalInternational, 191(2): 601-615.Frohlich C, Davis S D. 1999. How well constrained are well-constrained T, B, and P axes in moment tensor catalogs?.JournalofGeophysicalResearch:SolidEarth, 104(B3): 4901-4910.

Gilbert F, Dziewonski A M. 1975. An application of normal mode theory to the retrieval of structural parameters and source mechanisms from seismic spectra.PhilosophicalTransactionsoftheRoyalSocietyA:Mathematical,PhysicalandEngineeringSciences, 278(1280): 187-269. Han L B, Zheng Y, Ni S D. 2007. Parallelization of F-K method of synthetic of seismograms.JournalofUniversityofScienceandTechnologyofChina(in Chinese), 37(8): 911-915.

Hardebeck J L, Shearer P M. 2002. A new method for determining first-motion focal mechanisms.BulletinoftheSeismologicalSocietyofAmerica, 92(6): 2264-2276.

Hardebeck J L, Shearer P M. 2003. Using S/P amplitude ratios to constrain the focal mechanisms of small earthquakes.BulletinoftheSeismologicalSocietyofAmerica, 93(6): 2434-2444.

Haskell N A. 1953. The dispersion of surface waves on multilayered media.BulletinoftheSeismologicalSocietyofAmerica, 43(1): 17-34.

He X H, Ni S D, Liu J. 2015.Rupture directivity of the August 3rd, 2014 Ludian earthquake (Yunan, China).ScienceChinaEarthSciences, 58(5): 795-804, doi: 10.1007/s11430-015-5053-2.Helmberger D V. 1974. Generalized ray theory for shear dislocations.BulletinoftheSeismologicalSocietyofAmerica, 64(1): 45-64. Huang Y H, Meng L S, Ampuero J P. 2012. A dynamic model of the frequency-dependent rupture process of the 2011 Tohoku-Oki earthquake.Earth,PlanetsandSpace, 64(12): 1061-1066. Kanamori H, Rivera L. 2008. Source inversion of W phase: speeding up seismic tsunami warning.GeophysicalJournalInternational, 175(1): 222-238. Kikuchi M, Kanamori H. 1991. Inversion of complex body waves—III.BulletinoftheSeismologicalSocietyofAmerica, 81(6): 2335-2350.

Komatitsch D, Tromp J. 2002. Spectral-element simulations of global seismic wave propagation—I. Validation.GeophysicalJournalInternational, 149(2): 390-412.

Langston C A, Helmberger D V. 1975.A procedure for modelling shallow dislocation sources.GeophysicalJournaloftheRoyalAstronomicalSociety, 42(1): 117-130.

Luco J E, Apsel R J. 1983. On the Green's functions for a layered half-space. Part I.BulletinoftheSeismologicalSocietyofAmerica, 73(4): 909-929.

Ma S T. 2010.Focal depth determination for moderate and small earthquakes by modeling regional depth phases sPg, sPmP, and sPn.BulletinoftheSeismologicalSocietyofAmerica, 100(3): 1073-1088.

Mccaffrey R, Zwick P, Abers G. 1991. SYN4 program. IASPEI Software Library, 3: 81-166.

Montelli R, Nolet G, Dahlen F A, et al. 2004. Finite-frequency tomography reveals a variety of plumes in the mantle.Science, 303(5656): 338-343, doi: 10.1126/science. 1092485.

Ni S D, Helmberger D V. 2003. Ridge-like lower mantle structure beneath South Africa.JournalofGeophysicalResearch:SolidEarth, 108(B2)：2094-2106.

Ritsema J, Deuss A, Van Heijst H J, et al. 2011. S40RTS: a degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements.GeophysicalJournalInternational, 184(3): 1223-1236.

Shi Y L, Zhu S B. 2003.Contrast of rheology in the crust and mantle near Moho revealed by depth variation of earthquake mechanism in continental China.ChineseJ.Geophys.(in Chinese), 46(3): 359-365, doi: 10.3321/j.issn:0001-5733.2003.03.013.Sipkin S A. 1982. Estimation of earthquake source parameters by the inversion of waveform data: synthetic waveforms.PhysicsoftheEarthandPlanetaryInteriors, 30(2-3): 242-259.

Spence W. 1980.Relative epicenter determination using P-wave arrival-time differences.BulletinoftheSeismologicalSocietyofAmerica, 70(1): 171-183.

Tichelaar B W, Ruff L J. 1989. How good are our best models? Jackknifing, bootstrapping, and earthquake depth.Eos,TransactionsAmericanGeophysicalUnion, 70(20): 593-606. Virieux J. 1986. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method.Geophysics, 51(4): 889-901.

Wang R J. 1999. A simple orthonormalization method for stable and efficient computation of Green′s functions.BulletinoftheSeismologicalSocietyofAmerica, 89(3): 733-741.

Wang W M, Zhao L F, Li J, et al. 2008. Rupture process of theMS8.0 Wenchuan earthquake of Sicuan China.ChineseJ.Geophys.(in Chinese), 51(5): 1403-1410, doi: 10.3321/j.issn:0001-5733. 2008.05.013.

Wei S J. 2009. Constraining source parameters with sparse network[Ph. D.](in Chinese).Hefei: School of Earth and Space Sciences, University of Science and Technology of China.

Wei S J, Zhan Z W, Tan Y, et al. 2012. Locating earthquakes with surface waves and centroid moment tensor estimation.JournalofGeophysicalResearch:SolidEarth, 117:B040309.

Wright T J, Parsons B E, Jackson J A, et al. 1999. Source parameters of the 1 October 1995 Dinar (Turkey) earthquake from SAR interferometry and seismic bodywave modelling.EarthandPlanetaryScienceLetters, 172(1-2): 23-37.

Wu J P, Ming Y H, Wang C Y. 2004. Source mechanism of small-to-moderate earthquakes and tectonic stress field in Yunnan province.ActaSeismologicaSinica(in Chinese), 26(5): 457-465, doi: 10.3321/j.issn:0253-3782.2004.05.001.

Xie X B, Zheng T Y, Yao Z X. 1992.Methods of synthetic seismograms—A review.ActaGeophysicaSinica(in Chinese), 35(6): 790-801.

Xu ZH, Wang S Y, Huang Y R, et al. 1989. The tectonic stress field of Chinese continent deduced from a great number of earthquakes.ActaGeophysicaSinica(in Chinese), 32(6): 636-647.

Yu Z L, Ni S D, Wei S J, et al. 2012. An iterative algorithm for separation of S and ScS waves of great earthquakes.GeophysicalJournalInternational, 191(2): 591-600.

Zhan Z W, Helmberger D, Simons M, et al. 2012. Anomalously steep dips of earthquakes in the 2011 Tohoku-Oki source region and possible explanations.EarthandPlanetaryScienceLetters, 353-354: 121-133.Zhang Y, Feng W P, Xu L S, et al. 2008. The tempo-spatial distribution of slip for 2008 Wenchuan earthquake.ScienceChina:EarthSciences(in Chinese), 38(10): 1186-1194. Zhao L S, Helmberger D V. 1994. Source estimation from broadband regional seismograms.BulletinoftheSeismologicalSocietyofAmerica, 84(1): 91-104. Zhu L P, Rivera L A. 2002. A note on the dynamic and static displacements from a point source in multilayered media.GeophysicalJournalInternational, 148(3): 619-627.

Zwick P, Mccaffrey R, Abers G. 1994. MT5 program.IASPEI Software Library, 4.

附中文参考文献

陈伟文, 倪四道, 汪贞杰等. 2012. 2010年高雄地震震源参数的近远震波形联合反演. 地球物理学报, 55(7): 2319-2328, doi: 10.6038/j.issn:0001-5733.2012.07.017.

陈运泰, 许力生. 2003. 青藏高原及其周边地区大地震震源过程成像. 地学前缘, 10(1): 57-62, doi: 10.3321/j.issn:1005-2321.2003.01.007.

崇加军, 倪四道, 曾祥方. 2010. sPL, 一个近距离确定震源深度的震相. 地球物理学报, 53(11): 2620-2630, doi: 10.3969/j.issn.0001-5733.2010.11.010.

韩立波, 郑勇, 倪四道. 2007. 理论地震图的F-K算法的并行实现. 中国科学技术大学学报, 37(8): 911-915.

何骁慧, 倪四道, 刘杰. 2015. 2014年8月3日云南鲁甸M6. 5地震破裂方向性研究. 中国科学: 地球科学, 45(3): 253-263.

石耀霖, 朱守彪. 2003. 中国大陆震源机制深度变化反映的地壳-地幔流变特征. 地球物理学报, 46(3): 359-365, doi: 10.3321/j.issn:0001-5733.2003.03.013.

王卫民, 赵连锋, 李娟等. 2008. 四川汶川8.0级地震震源过程. 地球物理学报, 51(5): 1403-1410, doi: 10.3321/j.issn:0001-5733.2008.05.013.

韦生吉. 2009. 稀疏台网震源参数方法研究[博士论文]. 合肥: 中国科学技术大学地球与空间科学学院.

吴建平, 明跃红, 王椿镛. 2004. 云南地区中小地震震源机制及构造应力场研究. 地震学报, 26(5): 457-465, doi: 10.3321/j.issn:0253-3782.2004.05.001.

谢小碧, 郑天愉, 姚振兴. 1992. 理论地震图计算方法. 地球物理学报, 35(6): 790-801.

谢祖军, 金笔凯, 郑勇等. 2013. 近远震波形反演2013年芦山地震震源参数. 中国科学: 地球科学, 43(6): 1010-1019.

许忠淮, 汪素云, 黄雨蕊等. 1989. 由大量的地震资料推断的我国大陆构造应力场. 地球物理学报, 32(6): 636-647.

张勇, 冯万鹏, 许力生等. 2008. 2008年汶川大地震的时空破裂过程. 中国科学D辑: 地球科学, 38(10): 1186-1194.

(本文编辑胡素芳)

基金项目国家重点基础研究发展计划项目(2014CB845901)及国家自然科学基金(41274069)资助.

作者简介钱韵衣，女，1990年生，硕士生，从事地震学研究. E-mail: yyqian@mail.ustc.edu.cn *通讯作者倪四道，男，研究员，主要从事地震学方面的研究. E-mail: sdni@whigg.ac.cn

doi:10.6038/cjg20160608 中图分类号P315

收稿日期2015-08-04，2016-08-10收修定稿

The effects of the core-reflected wave ScS on source parameters in inversion with teleseismic body waves

QIAN Yun-Yi1， NI Si-Dao2*

1SchoolofEarthandSpaceSciences，UniversityofScienceandTechnologyofChina，Hefei230026，China2StateKeyLaboratoryofGeodesyandEarth′sDynamics，InstituteofGeodesyandGeophysics，ChineseAcademyofSciences，Wuhan430077，China

AbstractTeleseismic body waves (P and SH waves) are essential for obtaining source parameters (focal depth, mechanism, magnitude etc.) of moderate-strong earthquakes (M5.5～7). However, ScS waves could complicate SH waveforms, especially at large distances where the time interval between the direct SH and ScS waves is smaller than the time window in inversion, which is not taken into account in current inversion methods with teleseismic body waves. Therefore, the artefacts in source parameters could be produced with such contaminated waveforms. Based on TEL3 and fk methods of synthetic seismograms, we use the Jackknifing method to quantitatively test the effects of ScS on focal depth and mechanism in CAPtel inversion. When ScS effect is not considered for body wave data in the epicentral distance range 70°～90°, there are systematic deviations of 8° for focal mechanism and 1 km for source centroid depth between the input and inverted parameters; while there still are system deviations of 5° for mechanism, even though the epicentral distance of data ranges from 40° to 90°. Thus, the deviations caused by ScS in the ray theoretical inversion of teleseismic body waves cannot be neglected.KeywordsTeleseismic body wave； Source parameters； Core-mantle boundary； ScS

钱韵衣，倪四道. 2016. 核幔边界反射震相ScS对远震体波反演震源参数精度影响.地球物理学报，59(6):2014-2027,doi:10.6038/cjg20160608.

Qian Y Y, Ni S D. 2016. The effects of the core-reflected wave ScS on source parameters in inversion with teleseismic body waves.ChineseJ.Geophys. (in Chinese),59(6):2014-2027,doi:10.6038/cjg20160608.