连续梁合龙段水化热温度研究

常　亮

(中铁十局集团有限公司, 山东济南 250101)



连续梁合龙段水化热温度研究

常亮

(中铁十局集团有限公司, 山东济南 250101)

【摘要】高性能混凝土在浇筑后发热速度快，发热量高，在浇筑早期容易引起较大的内外温差，导致表面产生较大拉应力，容易引起混凝土裂缝，因此在浇筑时要考虑水化热的影响。论文以某连续梁合龙段箱梁截面为研究对象，在箱梁中埋设温度传感器，并用Midas有限元软件建立水化热模型进行水化热分析。

【关键词】箱梁;水化热;有限元模型

随着我国交通事业的快速发展，大量的连续箱梁桥正在建设，且桥梁混凝土越来越多地采用高性能混凝土，高性能混凝土在浇筑后发热速度快，发热量高，在浇筑早期容易引起较大的内外温差，导致表面产生较大拉应力，容易引起混凝土裂缝[1]。箱梁一旦出现表面裂缝或贯穿性裂缝，将会对其结构的整体性、安全性和耐久性造成很大的影响，因此在浇筑时要考虑水化热的影响，以有效防止裂缝，保证工程质量[2]。

1温度监测

1.1工程概况

某(60 m+100 m+60 m)连续梁全长221.5 m(含两侧两端至边支座中心各0.75 m)，结构形式为3跨预应力混凝土连续箱梁，端支座处及边跨直线段和跨中截面中心处梁高为4.53 m，中支点截面处梁高6.83 m，全桥箱梁顶宽12.2 m，箱梁底宽6 m，箱梁横截面为单箱单室直腹板，顶板厚48 cm，腹板厚分别为45 cm、60 cm、90 cm、100 cm，底板厚由跨中的38 cm按圆曲线变化至中支点梁根部的97.6 cm，中支点加厚到140 cm；全桥共设5道横隔梁，分别设于中支点、端支点和中间跨跨中截面，中支点处设置厚2.5 m的横隔梁，边支点处设置厚1.45 m的端横梁，跨中合龙段设置厚0.4 m的中横隔梁，隔板设有孔洞，供检查人员通过。

1.2测点布置

为了准确地获取结构的温度场，在合龙段埋设14个温度传感器，箱梁内外各放置两个温度计来测量内外环境温度。温度监测中采用长JMT-36B温度传感器(图1)，其具有高精度、高稳定性，高可靠性，防潮及绝缘等优良性能，适应长期监测和自动化测量。读数仪器为JMZX-300X综合测试仪(图2)，温度传感器具体布置如图3所示。将温度传感器绑扎在钢筋上，测试导线引到混凝土表面以方便采集数据。

图1　温度传感器

图2　JMZX-300X 综合读数仪

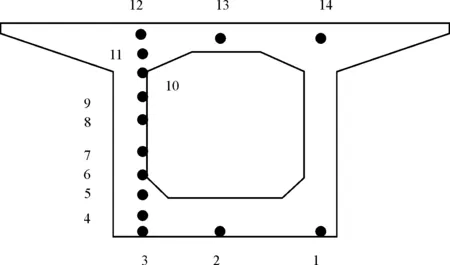
图3　合龙段截面温度测点布置图

1.3温度观察

合龙段浇筑后24 h的水化热温度观测记录见表1。

2 施工水化热模拟

2.1水化热理论

2. 1.1混凝土水化热与混凝土绝热温升理论

混凝土水化热有限元计算中需要用到混凝土水化产热率和绝热升温理论。混凝土水化热是依赖于龄期的，可以有三种表达式。

(1)指数式。

(1)

式中:Q(τ)为在龄期τ时的累积水化热总量；

Q0为τ→∞时的最终水化热(kJ·kg-1)；

τ为龄期(d)；

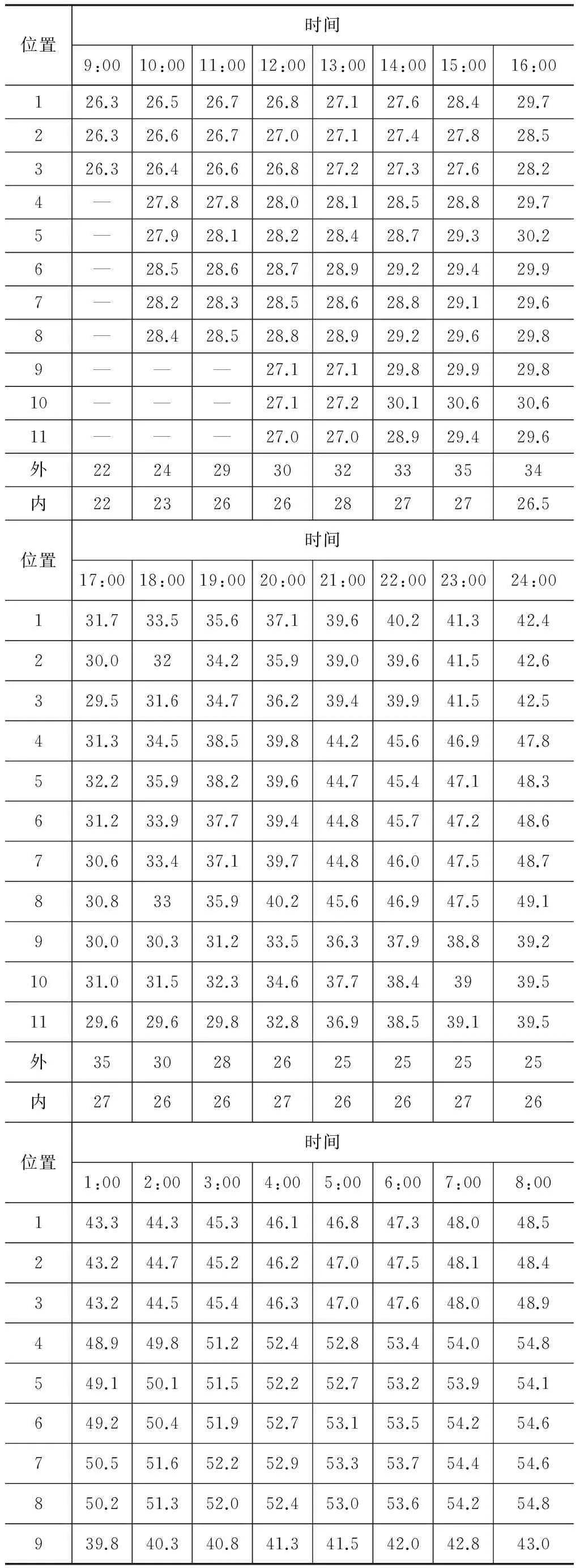
表1　合龙段浇筑后24 h水化热温度　℃

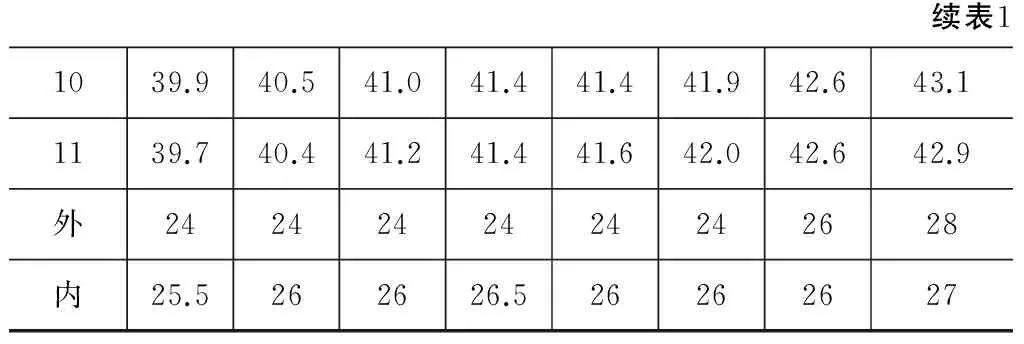
续表11039.940.541.041.441.441.942.643.11139.740.441.241.441.642.042.642.9外2424242424242628内25.5262626.526262627

m为与混凝土种类和浇筑温度有关的系数，数值见表2。

表2　常数m

(2)双曲线式。

(2)

式中:n为水化热产热量达到Q0/2时的混凝土龄期。

(3)复合指数式。

(3)

式中：a、b值通过试验求得(表3)。

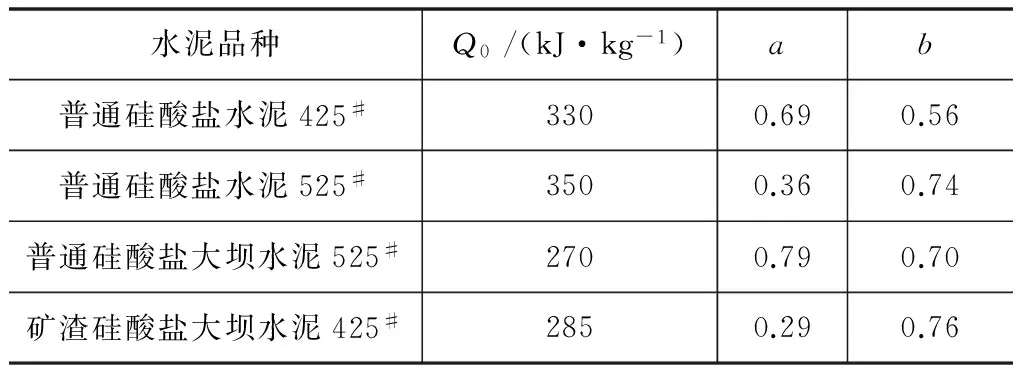
表3　水泥水化热常数

混凝土绝热温升θ是指混凝土结构在密闭绝热不产生任何能量损失的条件下，水化热产生的能量全部转化成混凝土结构内能时，结构所能达到的最高温度值。在缺乏直接测定的资料时，混凝土绝热温升可根据水泥水化热估算如下(二式取其一)：

(4)

(5)

式中:Th为混凝土最大绝热温升(℃)；

mc为混凝土中水泥用量(kg·m-3)；

c为混凝土单位热容，取0.97(kJ·kgK-1)；

F为混凝土活性掺和料用量(kg·m-3)；

Q为水泥28 d水化热(表4)；

k为掺和料折减系数，粉煤灰取0.25～0.30。

绝热温升Th(τ)与龄期τ的关系也可用指数式、双曲线式或复合指数式表示：

(6)

(7)

(8)

式中各个参数与前式意义相同。

表4　不同品种、强度等级水泥的水化热

2.1.2边界条件

有限元计算中，热力学分析常用的边界条件有3种：

(1)第一类边界条件

结构边界上的温度已知或按照已知函数分布，公式表达为：

(9)

式中:Г为物体边界，其方向为逆时针方向；

Tw为已知边界温度(℃)；

f(x,y,τ)为已知边界温度函数(时间，坐标的函数)。

(2)第二类边界条件

结构边界上的热流密度已知，公式表达为：

(10)

式中:q2为已知边界热流密度；

g(x,y,τ)为已知边界热流密度函数(时间，坐标的函数)。

(3)第三类边界条件

与结构相接触的流体介质温度Tf和对流换热系数α已知，公式表达为：

(11)

式中:β为结构表面放热系数；

Tf为与结构相接触的流体介质温度(℃)，工程中主要指空气温度或水温；

αS为结构表面日辐射热量吸收系数；

S为为日辐射强度。

2.1.3混凝土早期的弹性模量

根据文献资料，混凝土的早期弹性模量可以按下式计算：

(12)

式中:E(τ)为混凝土龄期为τ时弹性模量(MPa)；

E0为混凝土弹性模量，取标准条件下养护28 (d)的弹性模量；

φ为系数，应根据所用混凝土试验确定，当无试验数据时，可取0.09；

β为混凝土掺合料对弹性模量的修正系数，取值应以现场试验数据为准，无试验数据时可按下式计算。

掺合料修正系数计算公式：

(13)

式中:β1为混凝土中粉煤灰掺量对应的弹性模量修正系数；

β2为混凝土中矿渣粉掺量对应的弹性模量修正系数。

2.2建立水化热模型

2.2.1几个假定

使用Midas建立水化热模型时的几个基本假定；

(1)假定混凝土结构为均质体、各单元放热率相同；

(2)假定混凝土表面的放热系数为定值；

(3)不考虑结构内部钢筋的影响；

(4)混凝土浇筑的初始温度相同。

2.2.2建模的主要步骤

(1)结构建模；

(2)输入水化热分析数据；

(3)运行结构分析；

(4)查看分析结果。

模拟计算合龙段混凝土浇筑后7 d内的温度变化，加载时间为7 d，前24 h每隔一个小时建立一个步骤，后6 d以0.5 d为一个荷载步共分为36个荷载步。由于篇幅限制现在只把浇筑后48 h实测和理论计算的数据列出，计算模型见图4，图5、图6为混凝土浇筑后24 h的水化热云图，表5为合龙段浇筑后24 h后实测温度与模型计算值对比。

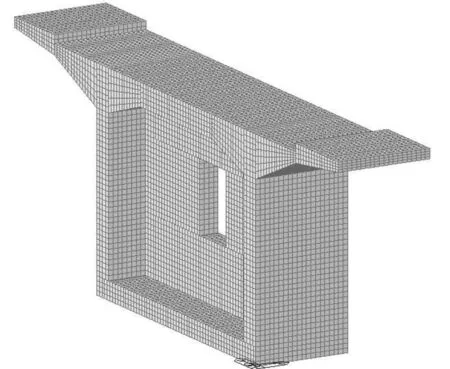
图4　实体单元水化热分析网格划分

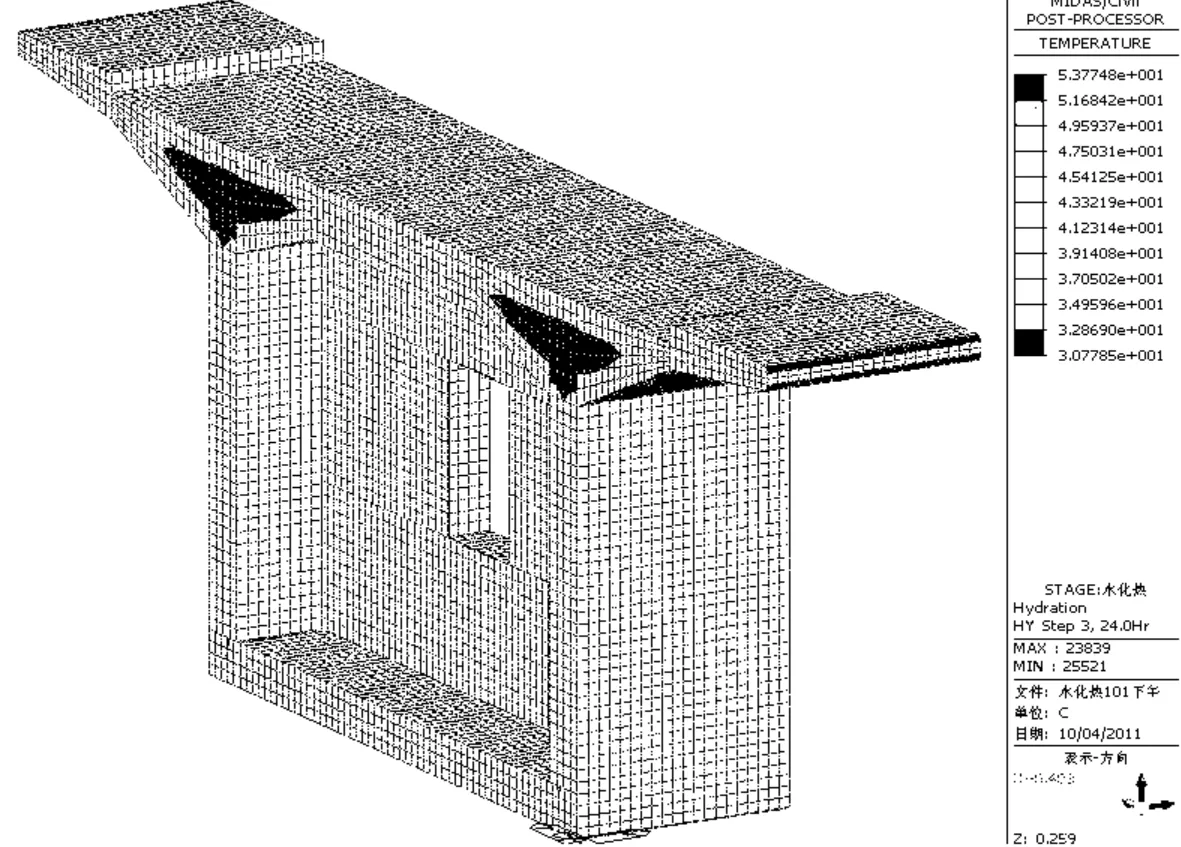
图5　浇筑后24 h温度场分布

图6　浇筑后24 h横隔板温度场分布

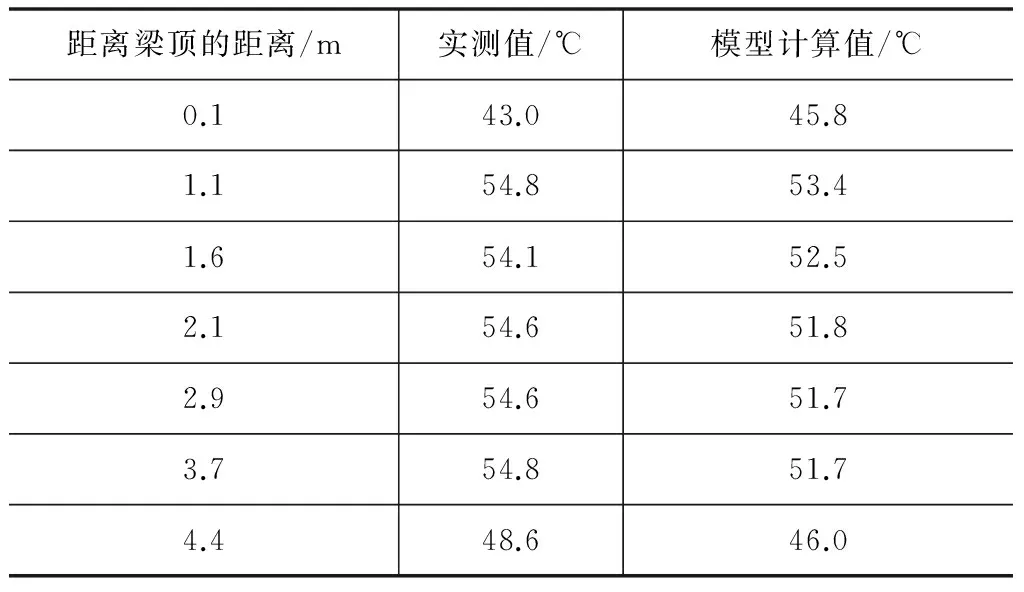
距离梁顶的距离/m实测值/℃模型计算值/℃0.143.045.81.154.853.41.654.152.52.154.651.82.954.651.73.754.851.74.448.646.0

由图5、图6、表5对比分析可以得知：梁顶实测水化热温度比计算数值略小，梁底和梁中的实测值略大于模型值说明实际箱梁产生的水化热比模型中的偏大，主要是由于梁顶和底板的对流条件与模型差异造成；实测底板温度比顶板温度偏高，因为梁底外部被模板包围，空气流动不如梁顶好；在结构对称、边界条件也对称时，温度场存在着对称性；理论数据比实测数据大10%左右，说明用Midas建立水化热模型对实际工程问题模拟具有一定的参考价值。

合龙段水化热温度最大值出现在混凝土浇筑后60 h，其端部和中部温度分布图如图7、图8所示。

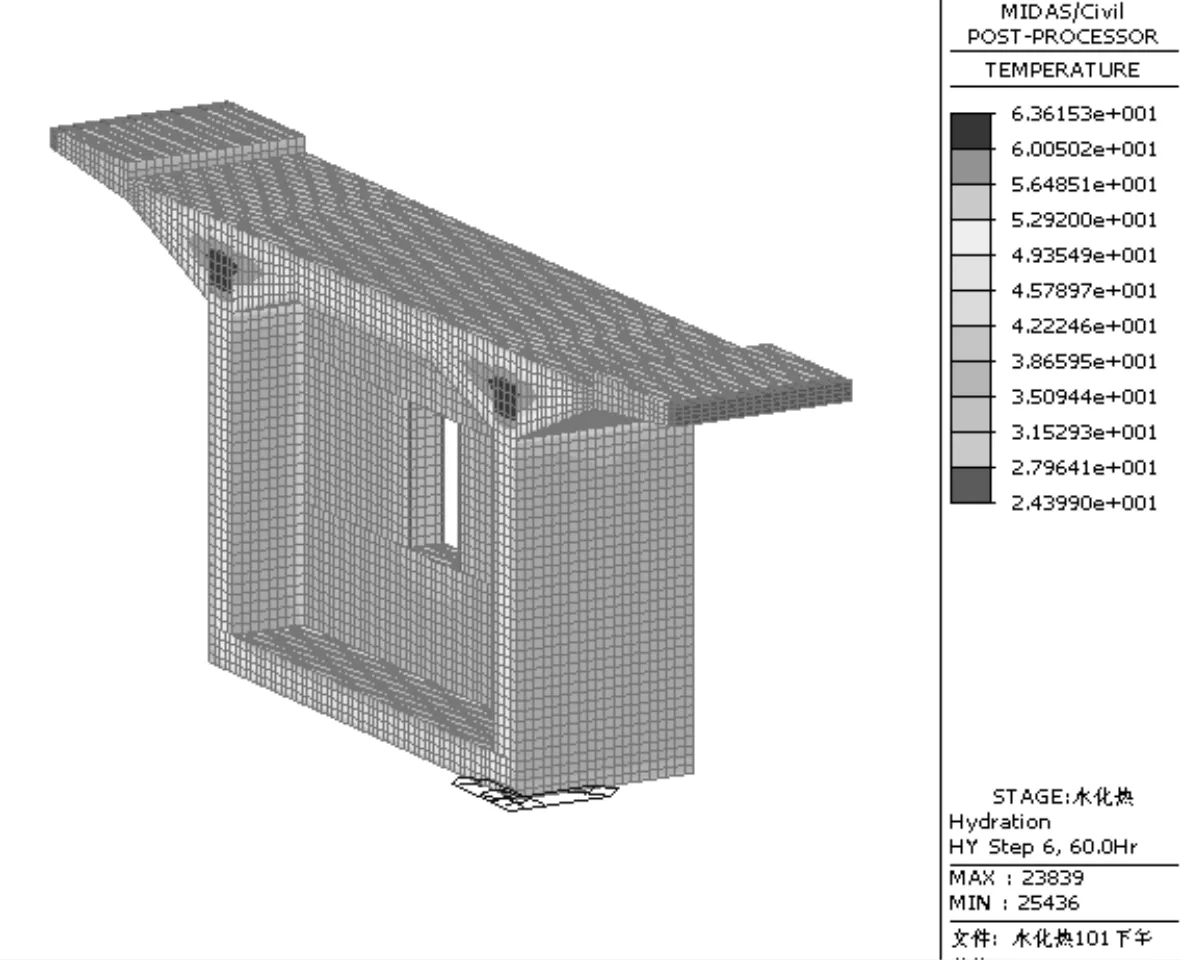
图7　浇筑后60 h温度场分布

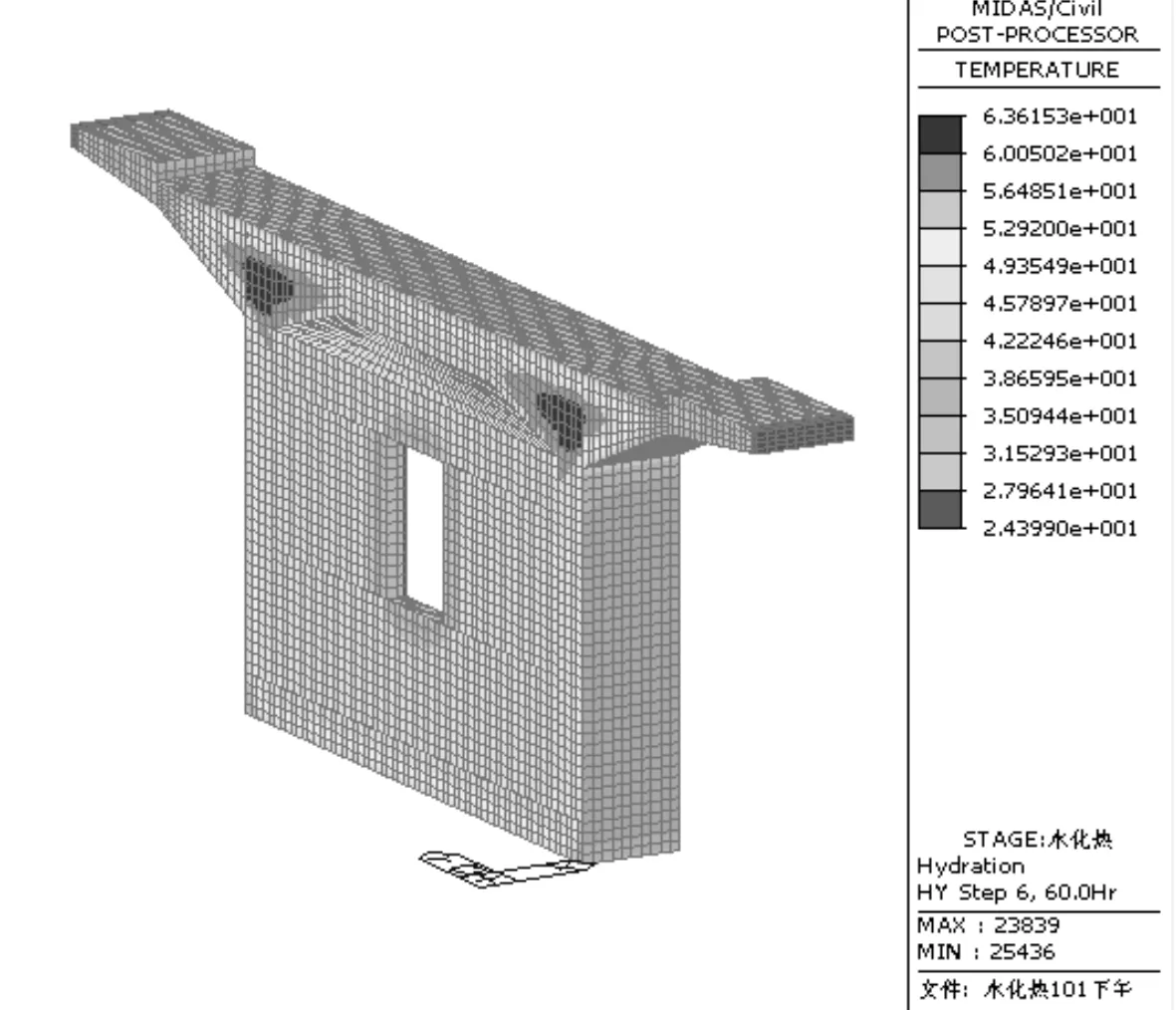
图8　浇筑后60 h横隔板温度场分布

由图7、图8可以看出，内部最高温度出现在腹板和翼缘板相交处，温度为63.6 ℃，截面内最低温度值为42.2 ℃，内

外温差最大值为21.4 ℃。混凝土内外温差不大于25℃，混凝土表面温度与环境温差16.2℃，不大于20℃，符合规范要求，在实测中没有发现裂缝产生。

3结束语

箱梁混凝土水化热产生的内外温差是温度裂缝的直接原因，合龙段箱梁的理论计算内外温差在规范要求范围内，理论计算和实测值基本吻合，用MIDAS建立水化热模型对实际工程问题模拟具有一定的参考价值。

参考文献

[1]王月胜.预应力混凝土连续箱梁施工控制研究和温度效应分析[D].成都：西南交通大学，2010.

[2]张景宏.混凝土水化热产生机理、危害与防治对策分析[J].科技向导,2011(8):245.

[3]刘来军.大跨径桥梁施工控制温度荷载[J].长安大学学报,2003, 23(2):61-62.

[4]冯德飞，卢文良.混凝土箱梁水化热温度试验研究[J].铁道工程学报,2006(8):62-67.

[5]卢文良, 季文玉, 杜进生. 铁路混凝土箱梁温度场及温度效应[J]. 中国铁道科学. 2006,27(6): 49-54.

[6]刘来君.大跨径桥梁施工控制温度荷载[J].长安大学学报：自然科学版,2003,23(2):61-63.

[7]赵剑锋.大跨度混凝土箱梁温度场及其效应研究[D].成都:西南交通大学,2010.

[8]黄毅.混凝土连续箱梁日照温度场及其效应研究[D].武汉:武汉理工大学,2009.

[9]张景宏.混凝土水化热产生机理、危害与防治对策分析[J].科技向导,2011(8):245.

[10]刘兴法.混凝土结构的温度应力分析[M].北京:人民交通出版社,1991.

[11]朱伯芳.大体积混凝土温度应力与温度控制[M].北京：中国电力出版社,1998.

[12]王金海. 预应力混凝土箱梁水化热裂缝控制与预防[J]. 公路工程,2012,37(2):172-176.

[作者简介]常亮(1986～),男,本科，工程师，从事铁路工程技术工作。

【中图分类号】TU755.6+7

【文献标志码】B

[定稿日期]2015-11-13