岩壁吊车梁单位长度吊车轮压计算方法研究

余玉志， 安旭文， 侯建国， 刘晓春

(1. 武汉大学土木建筑工程学院， 湖北武汉 430072； 2. 中南大学土木建筑学院， 湖南长沙 410083)



岩壁吊车梁单位长度吊车轮压计算方法研究

余玉志1， 安旭文1， 侯建国1， 刘晓春2

(1. 武汉大学土木建筑工程学院， 湖北武汉 430072； 2. 中南大学土木建筑学院， 湖南长沙 410083)

【摘要】结合我国电力系统行业标准《岩壁吊车梁设计规范》编制工作的需要，基于仿真材料模型试验成果，对岩壁吊车梁单位长度吊车轮压的不同计算方法进行了比较分析，提出了较为合理的岩壁吊车梁单位长度吊车轮压的计算方法和设计建议。对比分析结果表明，建议公式形式简单，概念明确，计算结果比较接近工程设计的实际采用值，偏于安全，且已为《岩壁吊车梁设计规范》报批稿采用。

【关键词】岩壁梁；轮压分布长度；单位长度吊车轮压

1岩壁吊车梁简介

在水电站地下厂房中，岩壁吊车梁(以下简称岩壁梁)是类似于壁式连续牛腿的结构形式，它是用锚杆将吊车梁锚固在地下厂房岩壁上，呈悬臂状态，吊车梁上的全部荷载通过梁上部的受拉锚杆传递到围岩深处，充分发挥围岩的作用。岩壁梁基本断面形式如图1。

图1　岩壁梁基本断面形式

岩壁梁最早是20世纪60～70年代在挪威等北欧国家开始应用并发展起来的[1-2]。20世纪80年代中期，我国率先在鲁布革水电站引入岩壁梁这种新型结构型式，并得到成功应用[3]。由于岩壁梁具有缩短地下厂房的跨度、减小开挖工程量、加快施工进度、节省投资等优点，近30多年来在国内水电站地下厂房中得到了广泛应用。我国现行电力行业标准DL/T 5198-2013《水电水利工程岩壁梁施工规程》[4]已于2013年8月颁布实施。然而，到目前为止，我国尚没有一本规范对岩壁梁结构的设计计算作出系统和明确的规定，国内各设计单位在具体的设计计算过程中所采用的设计方法也不统一，安全度设置水平差别较大。因此，为了在地下厂房中更好地推广应用这种新型结构型式，充分发挥岩壁梁的优越性，完善岩壁梁设计理论和方法，使岩壁梁的设计在安全可靠与经济合理之间达到最佳的平衡，本文结合《岩壁吊车梁设计规范》[5]编制工作的需要，总结近30年来岩壁梁在我国水电工程中广泛应用的成功经验，基于仿真材料模型试验成果，对岩壁梁单位长度吊车轮压的计算方法进行分析比较，为岩壁梁设计规范的编写提供理论依据。

2单位长度吊车轮压的计算方法

作用在岩壁梁上的荷载主要有吊车的竖向轮压、水平制动力、岩壁梁自重以及轨道和附件自重、梁上防潮隔墙及二期混凝土自重等。吊车轮压荷载作为岩壁梁承担的主要荷载，其合理取值是岩壁梁结构设计的关键问题之一。除采用三维有限元方法可以模拟吊车轮压沿岩壁梁长度方向的分布以外，若采用刚体极限平衡法或平面有限元方法，都必须将空间问题转化为平面问题来处理，将吊车轮压转化为等效均布荷载作用于单位长度的岩壁梁上，然后对岩壁梁进行受力分析。因此，采用刚体极限平衡法或平面有限元法等对岩壁梁进行受力分析前，必须确定单位长度上吊车的竖向轮压及横向水平刹车力的大小。吊车轮压的等效换算方法目前有很多种，包括经验法、建立在模型试验基础上的或者与有限元对比计算基础上的一定范围内的扩散等效法(竖向扩散、水平扩散)以及弹性地基梁法等等。但不同方法对单位宽度吊车荷载的计算结果不尽相同，有时甚至差别较大。因此，本文结合典型工程实例，在比较分析的基础上，提出岩壁梁吊车轮压计算宽度的合理计算方法及单位宽度轮压取值的设计建议。

吊车荷载包括吊车竖向荷载和吊车横向及纵向水平荷载(即水平制动力)，由于设计中对吊车横向水平荷载的计算都是取与竖向荷载相同的分布宽度，因此，这里以吊车竖向荷载为例，分析吊车轮压的分布宽度及单位长度上吊车轮压的计算方法。

水电站厂房中的吊车每边可以有2个、4个、8个或12个轮子，中等以上起重量的吊车每边一般有4～8个轮子。每边8轮时，吊车轮压及轮距分布如图2所示。现以一边8轮的吊车为例，将国内有关单位和专家学者提出的岩壁梁单位长度吊车轮压的计算方法介绍如下。

图2　吊车轮压及轮距分布

2.1“挪威”法

岩壁梁最早用于挪威等北欧国家，最初采用的单位长度吊车轮压的计算方法简称“挪威”法，它是直接用吊车一侧的总轮压除以考虑两侧轮压扩散范围和总轮距之和求得，即

(1)

式中：Pc为单位长度的吊车计算轮压(不包括动力系数)；P0为岩壁吊车梁一边所承受的吊车总轮压，当一边为8轮时，P0=8Pmax，Pmax为在桥机额定起重量下，作用于岩壁吊车梁顶面的桥机一侧轨道上的单个轮子的最大轮压(kN)，在吊车动载试验时，单个最大轮压可取为1.1Pmax；B0为吊车轮压的计算分布宽度，对于普通工程和大型工程，可分别按下式计算：

(2a)

(2b)

式中吊车轮距B1、B2、B3可按设计图样或设备供应商提供的数值采用。

该方法思路清晰，公式简洁，计算方便。对于普通工程，适当考虑了总轮距宽度以外的部分梁段与总轮距宽度以内的梁段共同承受吊车荷载的有利影响，提高了工程的经济性。而对于大型工程，不考虑该有利影响，直接将吊车轮压转化为均布荷载作用在总轮距宽度以内的岩壁吊车梁上，提高了工程的安全度[6-7]。我国乌江渡水电站扩机工程和拉西瓦水电站的岩壁梁单位长度吊车轮压即按不考虑轮压扩散情况下的挪威法(B0按公式(2b)计算)确定的。但该方法对于普通工程和大型工程没有明确的划分，在实际工程中使用时可能存在偏差。

2.2中间轮组法

这种方法假设中间轮组的作用范围主要集中在中间轮组及两侧各一半轮距的区域，将中间轮组的吊车轮压之和除以中间吊车轮压的分布范围确定单位宽度的吊车轮压计算值[8- 9]，即

(3)

中间轮组法实质上是假定中间轮组轮压作用的梁段为岩壁梁最危险梁段，将中间轮组的吊车轮压之和均匀地分布在可能分布范围内的梁段上。该公式表达形式简单，计算简便。我国广州抽水蓄能[9]、江垭[10]、小湾[11]、天荒坪[12]等水电站，均是采用中间轮组法确定岩壁梁单位长度的吊车轮压。这种方法对于中间轮组轮压作用附近梁段的受力用此方法来简化是基本合适的，但不考虑两边轮组轮压作用下岩壁梁的受力，仅认为中间轮组吊车轮压作用的岩壁梁梁段为最危险梁段，这一假定是否合适，需待进一步论证。

2.3单个轮压法(吴新邦法)

吴新邦认为，单个轮压的分布宽度应为(B1+B2)/2和2(hc+c1)中的较小值。该方法是将单个吊车最大轮压除以单个吊车轮压可能的分布宽度，求得单位长度的吊车轮压计算值[13]，即

(4)

式中：hc为吊车轨顶至岩壁梁一期混凝土顶面的距离；c1为吊车轮压作用点到上部墙面的水平距离(图1)。

单个轮压法概念明确，计算简便，适用范围较宽。但认为单个轮压仅在该轮左右两侧轮距各一半的范围内分布的假设偏于保守。

2.4弹性地基梁法

弹性地基梁法是将岩壁视为弹性地基，岩壁梁梁体结构视为地基梁[14]，按照吊车轮压作用下梁的最大变位Wmax与单位长度的岩壁梁脱离体在吊车计算轮压作用下变位相等的原则(即wmax=w，如图3所示)，求得单位长度的吊车轮压计算值，即

(5)

式中：λ为文克尔地基梁的柔度特征值；xi为变位计算点离第i个集中力的距离。

由公式(5)可以看出，按弹性地基梁法计算单位长度的吊车轮压值，关键是求参数Amax。当xi=3π/4λ时，A(xi)=0。因此，轮压计算长度只在3π/2λ内有效，Amax是在长度3π/2λ范围内吊车轮压分布最大时吊车轮压长度中心所对应的A值，适用于一边2轮、4轮和8轮等情况。

弹性地基梁法能较好地模拟岩壁梁的实际受力情况，且计算理论较为成熟，由此计算的单位宽度吊车轮压计算值较小，与中间轮组法基本相近，用于实际工程设计比较经济。东风、龙滩、大广坝水电站岩壁梁单位长度的吊车轮压采用弹性地基梁法确定[7, 15, 16]。但这种方法在计算中吊车轨道和二期混凝土的作用难于模拟，同时由于计算中涉及到较多的参数，参数取值也存在较大的不确定性，且计算过程比较复杂。

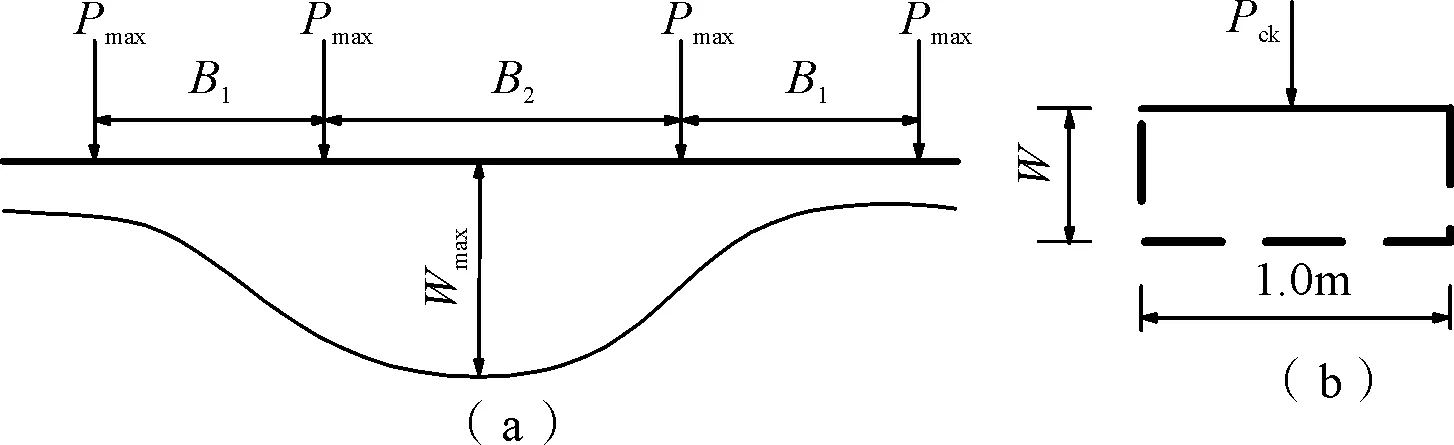
(a)岩壁梁在吊车荷载作用下的变形(b)单位长度脱离体在吊车计算轮压下的变形图3　吊车轮压等效荷载计算示意

2.5等效三角形荷载法

按照传统的力系平衡法设计岩壁吊车梁时，取单位长度的梁为脱离体，单位长度的吊车轮压取值一般是将吊车一侧总轮压除以一可能的受力范围，作为均布荷载作用于脱离体上，且为了保证岩壁梁的安全，实际计算中一般取各种方法计算Pc值的较大值，由此求得的单位长度吊车轮压计算值Pc往往偏大，且没有考虑岩壁梁竖向抗剪承载力的影响。根据岩壁梁三维有限元计算结果和实测应力的对比分析，文献[17]认为由于岩壁梁抗剪力的存在，吊车轮压主要是由其作用点左右两侧一定范围内的倾斜岩台台面上的法向力及切向力承担，这就产生了“荷载扩散的三维效应”，从而减小了岩台台面上的压应力。实际计算中，将按总轮压除以总轮距宽度法所求得的轮压值乘以轮压扩散的折减系数δ，即

(6)

其中，考虑轮压扩散的折减系数δ可根据有限元分析的计算结果按等效三角形荷载法确定(图4)，将吊车轮压在岩壁梁上的分布简化为从轮距中点向两边呈递减的三角形分布，按照总荷载不变的原则确定，即

(7)

(8)

图4　轮压扩散示意

根据岩壁梁有限元计算结果，近似取B=B0+nh(h为岩壁梁的断面高度)，根据文献[13]中的设计参数，求得n=4.8，即轮压实际扩散宽度B=B0+4.8h。由此求得轮压扩散的折减系数δ为：

(9)

该方法考虑了岩壁梁竖向剪切力的影响，从文献[17]三维应力分析的结果来看，能较好地模拟吊车轮压在岩壁梁上的分布情况，但这个结果仅仅是根据一个实际工程——东风

水电站岩壁梁的三维应力分析得出的轮压折减系数δ，是否适用于其它工程，还有待进一步探讨。

2.6基于模型试验结果的方法

武汉大学20世纪90年代初完成的龙滩水电站地下厂房岩壁吊车梁仿真材料模型的试验结果表明，沿岩壁梁的长度方向，实测受拉锚杆的应变呈曲线分布，在吊车轮压点处受拉锚杆应变达到最大值，随着离开吊车轮压点的距离的增大，受拉锚杆的拉应变逐渐减小，说明岩壁梁设计时应考虑吊车轮压分布宽度的影响。

基于模型试验结果的单位长度吊车轮压简化算法的思路是：假定吊车轮压分布宽度内的抗裂弯矩与吊车轮压产生的弯矩相等，求得轮压的计算宽度B0，进而求得单位长度吊车轮压的计算值。简化算法适当考虑了吊车轮压的扩散影响，吊车计算轮压宽度接近于从吊车轮压作用点约26°角向交界面处平面扩散的宽度(图5)。试验结果表明，当岩壁梁模型在吊车轮压作用下接近破坏时，按上述原则确定的吊车轮压分布宽度内锚杆的应变均已达到屈服应变值，能共同承受吊车轮压所产生的弯矩。基于上述试验结果，建议单位长度吊车轮压可按下列公式计算：

Pc=P0/B0

(10)

吊车一侧4轮或8轮时，按4轮组计算：

(11)

统计分析结果表明，基于仿真材料模型试验成果建立的适当考虑吊车轮压扩散作用的简化算法，略大于其他算法的计算结果，比较接近工程设计的实际采用值，公式形式简单，概念明确，是工程经验的总结，且偏于安全。

上述公式是基于岩壁吊车梁仿真材料模型试验结果建立的。从受力机理和吊车荷载传递特点来看，河床式、地下式和坝内式水电站厂房中的壁式连续牛腿与岩壁吊车梁相似，故我国电力行业标准DL/T 5057-2009《水工混凝土结构设计规范》[18]在修订时，根据上述岩壁梁仿真材料模型试验成果对原规范中壁式连续牛腿单位长度吊车轮压的计算值按上述计算方法进行了修订。考虑到岩壁梁和壁式连续牛腿受力特点和传力机理的相似性，同时也为了规范之间相互协调和引用，建议在《岩壁吊车梁设计规范》中，按上述计算方法确定岩壁梁单位长度吊车轮压的计算值。

图5　基于模型实验结果单位长度吊车轮压计算图式

2.7吊车轮压45°扩散法

实际工程中也有采用将中间几个轮压的宽度按45°扩散，作为轮压分布宽度来计算单位长度岩壁吊车梁上的吊车轮压，如长江委设计院在对江口水电站岩壁吊车梁进行试设计时，将3个轮压按45°扩散来推求这3个轮压的分布宽度[19]。

吊车轮压45°扩散法是将最边缘的吊车轮压通过轨道、垫板、二期混凝土按45°角扩散至岩壁吊车梁一期混凝土表面，两最远扩散点之间的距离作为轮压的分布宽度，即

(12)

该方法考虑了总轮距宽度以外的梁段与总轮距宽度以内的梁段共同承受吊车轮压的有利影响，得出的单位梁长度吊车轮压比总轮压除以总轮距宽度的计算结果要小。

3不同计算方法的计算结果比较

根据前述不同计算方法所给出的单位长度吊车轮压的计算公式，本文选择目前资料收集比较完备的广蓄、东风、江口、江垭、乌江渡、龙滩、黑麋峰等7座水电站岩壁梁吊车梁的基本设计参数，对各种计算方法进行了计算分析。按照上述方法求得单位长度吊车轮压计算结果见表1。为便于比较，表1还同时给出了各水电站岩壁梁设计中单位长度吊车轮压的实际采用值。

由表1计算结果可以看出：目前国内所采用的几种岩壁梁单位长度吊车轮压计算方法中，中间轮组法的计算结果最小。其他的几种方法，当轮压和轮距变化时，单位长度吊车轮压的相对大小的规律性不明显。对于一边8轮的情况，按照基于模型试验法计算轮压的分布长度时，吊车轮压的计算结果略小于挪威法不考虑轮压扩散时的计算结果，但是在几个大型工程中，B3/B1的比值较大时，前者大于后者。但总体来看，采用基于模型试验法得出的单位长度的吊车轮压与工程实际采用的吊车轮压最为接近。与其他方法相比，弹性地基梁法考虑的因素比较全面，能够考虑围岩的岩性及梁体刚度对岩壁梁轮压分布宽度的影响，但是围岩的参数取值难以确定，计算过程比较繁琐，一般需采用计算机程序进行计算。

表1　不同计算方法单位长度吊车轮压计算结果的比较

注：1. 除乌江渡水电站为壁式连续牛腿外，其余工程均为岩壁吊车梁； 2. 江口、黑麋峰工程由于地质资料不详, 未能按弹性地基梁法计算； 3. 上表中Pc均为扣除动力系数影响后的值。

4主要结论

首先，弹性地基梁法和数值分析法表明，岩壁梁的最大轮压一般出现在轮距为B1和B2的4个或6个轮压的中部，可见对轮距为B1和B2的4个或6个轮压进行分析更为合理。因此，基于模型试验提出的单位梁长吊车轮压的简化计算公式中按轮距为B1及B2的4个或6个轮压考虑是较为合适的。其次，由于岩壁梁主要是用来承担吊车荷载引起的横向弯矩，因而主要是一个横向的受力体系，吊车轮压按照横向受力体系考虑水平方向的扩散才是比较合理的。由此可见，基于模型试验提出的单位梁长吊车轮压的简化计算公式反映了岩壁吊车梁上吊车轮压的传力机理，考虑轮压横向水平扩散是比较合理的。最后，弹性地基梁法与基于仿真材料模型实验法的计算结果吻合较好；吊车轮压作用下岩壁吊车梁的三维有限元分析结果，与基于仿真材料模型实验法的计算结果也基本一致。

因此，基于岩壁梁仿真材料模型试验成果建立的适当考虑吊车轮压扩散作用的简化算法，反映了岩壁梁上吊车轮压的传力机理，力学概念明确，应用简便，计算结果与其他算法相比更加合理，且比较接近工程设计的实际采用值。同时，考虑到壁式连续牛腿与岩壁梁受力特征的相似性，为了与我国已颁布的电力行业标准相协调，建议将基于模型试验成果建立的计算方法作为计算单位长度吊车轮压的计算方案，供规范修订组选用和参考。

而对于一些复杂或特别重要的岩壁吊车梁设计，可采用弹性地基梁法、三维有限元分析法或现场模型试验等方法综合确定。

参考文献

[1]谷兆祺，李新新，郭军．挪威水电工程经验介绍[M]. 北京: 水利电力出版社， 1985.

[2]侯建国(译)．挪威地下式水电站厂房中的悬臂吊车梁[J]．水利电力科技，1994 (1): 53-56.

[3] 王裕湘．鲁布革水电站地下厂房岩壁吊车梁设计[J]．水力发电，1988(12): 52-54.

[4] DL/T 5198-2013 水电水利工程岩壁梁施工规程[S]．北京：中国电力出版社，2013.

[5] 岩壁吊车梁设计规范(报批稿)．2015.

[6] Lien R. , Kristiansen J. and Pran L. S. Suspended support for crane rails in Norwegian underground powerhouses[J]. Water Power & Dam Construction，1990，42(4): 48-50.

[7]汪基伟, 刘瑞．任意荷载作用下带形牛腿轮压分布宽度计算方法[G]．水工结构工程理论与实践．北京：科学技术文献出版社，1999: 352-356.

[8]程晓鸣，刘正军．引黄入晋工程总干1#、2#泵房岩壁吊车梁锚固设计[J]．水利水电工程设计, 2000(1): 3-5.

[9]陈颖豪，卓美珍．广蓄岩壁吊车梁的设计与实践[J]．水力发电, 1993(7): 27-29.

[10]喻伟明．江垭电站地下厂房岩壁吊车梁的设计[J]．湖南水利，1998(3): 3-5.

[11] 洪振伟．小湾水电站地下厂房吊车梁设计[J]．云南水力发电，1996(3): 71-75.

[12] 应和平，刘郁子．天荒坪抽水蓄能电站地下厂房岩壁吊车梁设计[J]．华东水电技术，2000(2): 119-123.

[13] 吴新邦．岩锚式吊车梁的设计[J]．水力发电，1995(3): 28-32.

[14] 周氐，章定国，钮新强．水工混凝土结构设计手册[M]．北京：中国水利水电出版社，1999.

[15] 周帆，杨伏秋，张孝松. 龙滩水电站地下厂房岩锚吊车梁设计[J]．红水河，2004，23(2):110-113.

[16] 曹普发, 肖传豹．东风水电站地下厂房岩锚吊车梁的设计及其承载试验[J]．水力发电, 1994(12): 19-22.

[17] 刘颖，曹普发，彭守拙．轮压作用下岩壁吊车梁的三维应力和实测对比[J]．水力发电学报，1996(2): 51-61.

[18] DL/T 5057-2009 水工混凝土结构设计规范[S]．

[19] 史济民，掌于昶．江口水电站岩锚吊车梁设计[J]．东北水利水电，2002,20(1):4-5.

[20] 刘进宝, 刘迎曦, 李守巨. 岩锚吊车梁轮压效应的三维有限元数值分析[J]. 水利水电技术, 2004(9): 54-58.

[21] 刘春霞. 地下厂房中岩壁式吊车梁的结构分析与稳定性计算[D]. 南京: 河海大学, 2006.

[22] 隋斌, 朱维申, 李树忱. 岩锚吊车梁轮压作用下的三维稳定性分析[J]. 山东大学学报: 工学版, 2008, 38(1): 80-83,108.

[作者简介]余玉志(1984～)，男，硕士。

[通讯作者]安旭文(1970～)，男，博士，副教授，主要从事工程结构可靠度理论与应用研究。

【中图分类号】TV31

【文献标志码】A

[定稿日期]2015-12-17