斜拉桥钢-混结合段刚度和位置的影响分析

许圣祥, 霍学晋

(1. 四川巴陕高速公路有限责任公司, 四川成都 610041;2. 中铁大桥勘测设计院有限公司, 湖北武汉 430056)



斜拉桥钢-混结合段刚度和位置的影响分析

许圣祥1, 霍学晋2

(1. 四川巴陕高速公路有限责任公司, 四川成都 610041;2. 中铁大桥勘测设计院有限公司, 湖北武汉 430056)

【摘要】某斜拉桥为双塔双索面斜拉桥，使用有限元分析软件Midas建立斜拉桥的有限元计算模型，分析钢-混结合段刚度和位置的变化，研究其对全桥的位移、内力、自振特性和稳定系数的影响。计算与分析结果为该类型桥的设计提供了一定的参考价值。

【关键词】斜拉桥;结合段;刚度;位置;影响

斜拉桥的受力由主梁、主塔和斜拉索共同决定。钢-混结合段是连接钢箱梁和混凝土箱梁的重要构件，其自身刚度和设置位置直接影响主梁乃至全桥的受力。本文通过改变钢-混结合段的刚度和位置，研究其对斜拉桥全桥的位移、内力、自振特性和稳定系数的影响[1]。

1全桥杆系有限元模型

塔、梁、墩及桩基础采用空间梁单元，索采用只受拉的索单元模拟，结合段的刚度利用换算截面法进行计算，建立的全桥空间杆系有限元模型如图1所示。

图1　全桥杆系有限元模型

2结合段刚度的影响

假定原设计钢-混结合段刚度的惯性矩为I，取5种不同的惯性矩0.25I、0.5I、I、2I、4I分别进行计算，研究结合段刚度对位移、内力、自振特性和稳定系数的影响[2]。

2.1结合段刚度对位移和内力的影响

选取跨中和结合面的挠度、塔顶的横向位移、结合面和跨中截面的轴力和弯矩、边跨和中跨的1#、10#和19#索(边跨和中跨索的编号均为从塔向两侧的顺序，近塔为1#索，最远端为19#索)的索力为对象，研究结合段刚度对位移和内力的影响。表1为不同结合段刚度下的位移、内力和索力，施加的荷载为自重荷载。

由表1可知，由于该斜拉桥的主跨为608 m，而结合段长度仅为2 m，且靠近塔根处，改变结合段的刚度对跨中挠度的影响不大，可忽略不计。结合段刚度对结合面处的挠度略有影响，4倍刚度时相对0.25倍刚度结合面挠度增大了16.5%，但此处靠近桥塔，挠度值并不大。由表1还可看出，塔顶的横向位移受结合段刚度的影响也不大，跨中截面的轴力和弯矩整体上随着结合段刚度的增大略有降低，但整体上影响不大。结合面处的轴力和弯矩受自身刚度的影响较为明显，尤其是弯矩，4倍刚度下相对0.25倍刚度增大了28.9%。随着索在主梁上的锚固点到结合面的距离越大，该索的索力受结合段刚度的影响越小，如中跨和边跨的19#索。

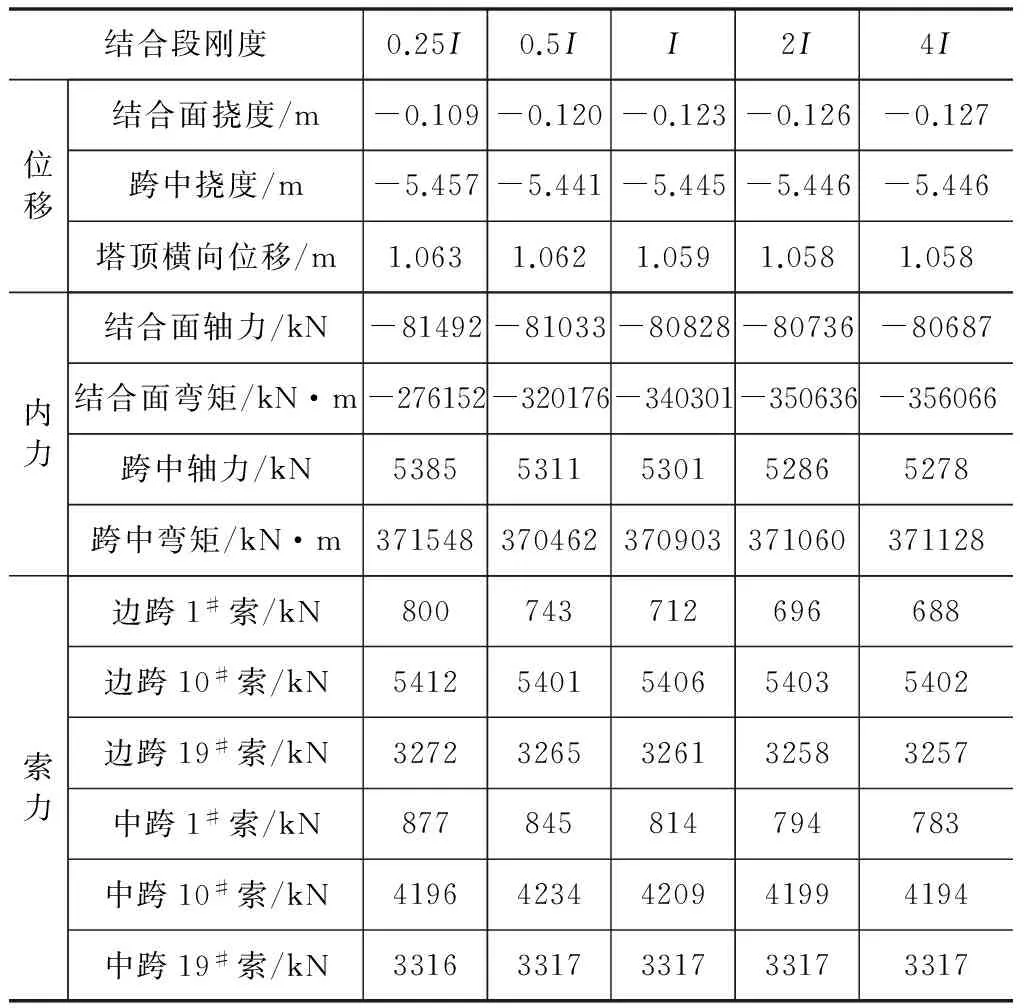
表1　结合段刚度对位移和内力的影响

综上所述，结合段刚度的改变对结合段附近的梁段和索力影响较大，但对距离结合段较远的梁段和索力影响很小。

2.2结合段刚度对自振特性和稳定系数的影响

结构的自振特性与刚度分布直接相关。表2为不同结合段刚度下结构的前八阶频率[3]，图2为前四阶振型。

由图2可知，结构的第一阶振型为主梁的纵漂，第二阶和第四阶为主梁的竖弯变形，而第三节为主梁的横弯。由表2可知，由于只改变了结合段的竖向弯曲刚度，纵漂的第一阶

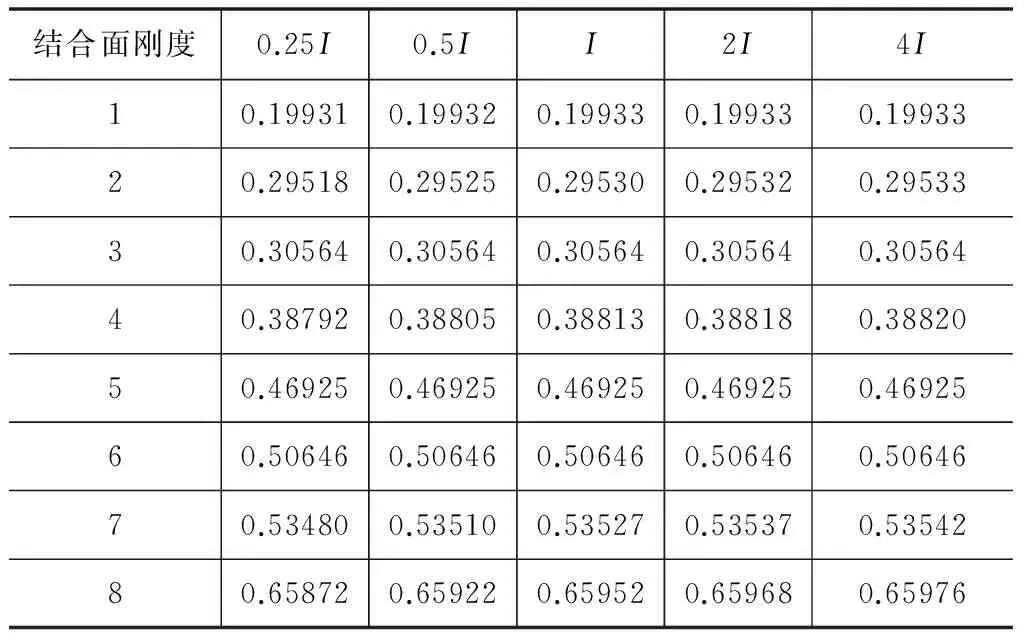
表2　结合段刚度对自振频率的影响

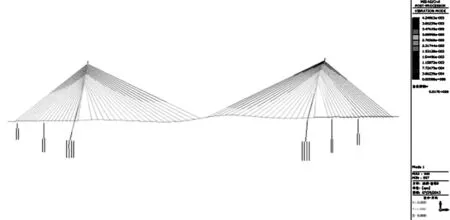
(a)第一阶(纵向漂移)

(b)第二阶(主梁的竖向一阶)

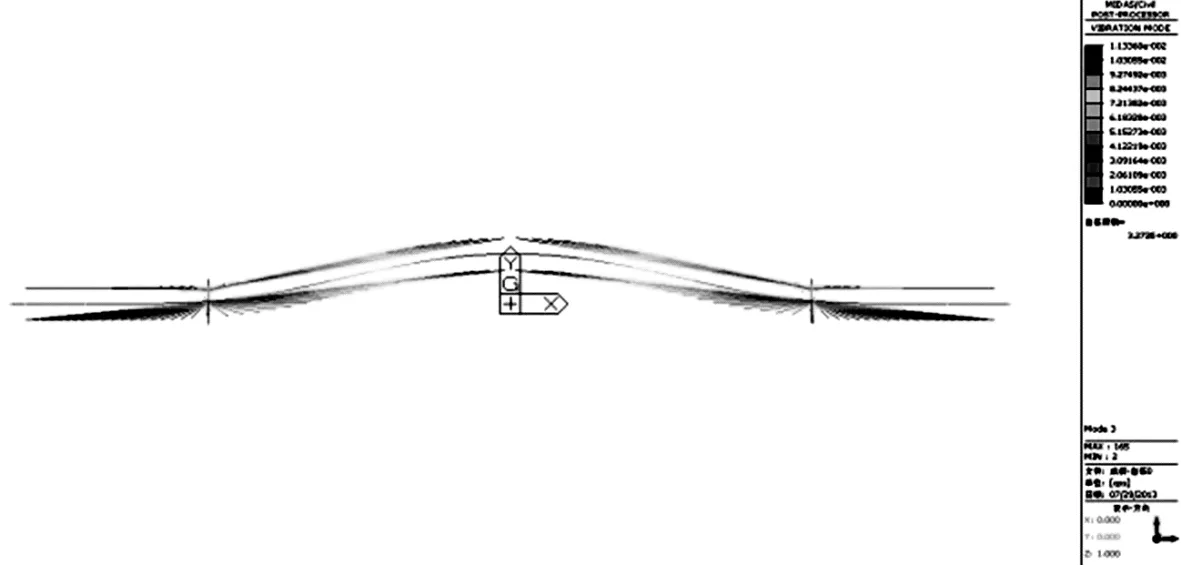
(c)第三阶(主梁的横向一阶)

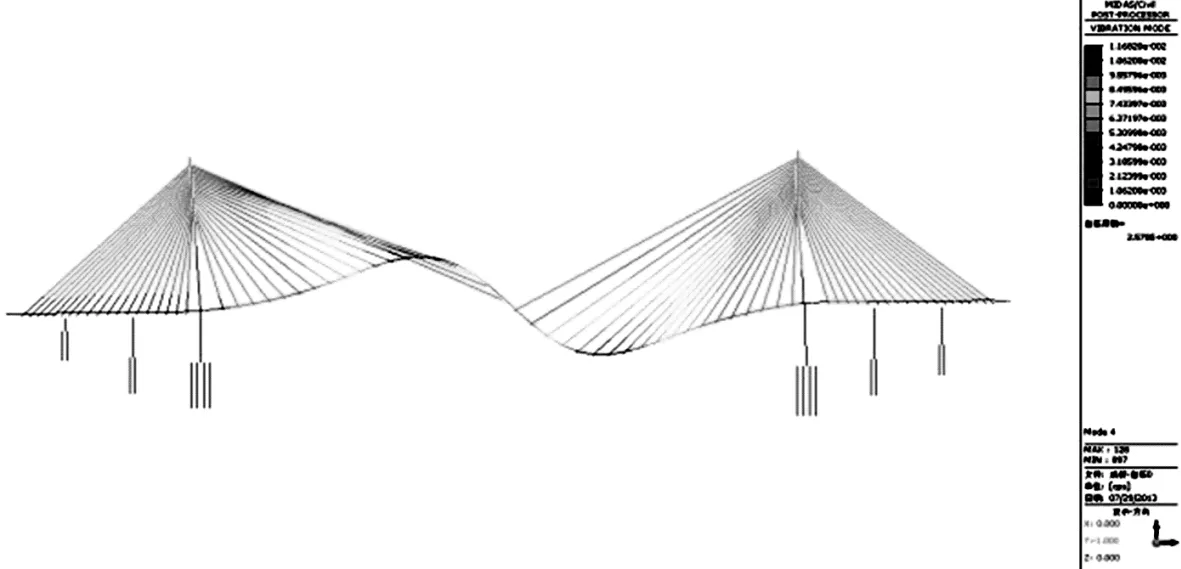
(d)第四阶(主梁的竖向二阶)图2　前四阶振型

频率和横弯的第三阶频率受结合段刚度的影响均较小，可忽略不计，而第二阶和第四阶频率随着结合段刚度的增大而略有增大。

表3为不同结合段刚度下结构的前两阶稳定系数[4]，图3为前两阶失稳模态。

由表3可知，结构的前两阶稳定系数均随着结合段刚度的增大略有增大，但由于结合段长度相对跨度较短，其对稳定系数的影响程度并不大，在设计时可不考虑其对整体稳定性的影响。

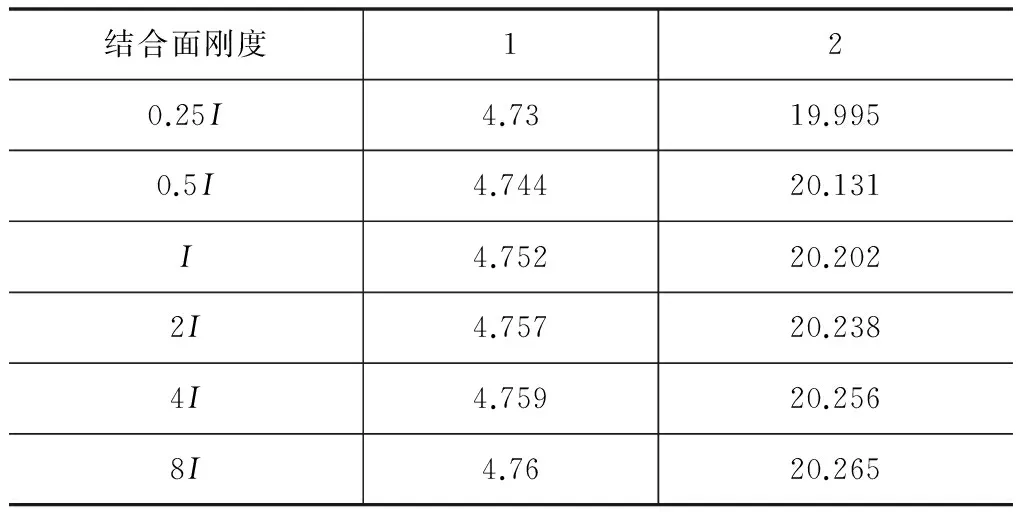
表3　结合段刚度对稳定系数的影响

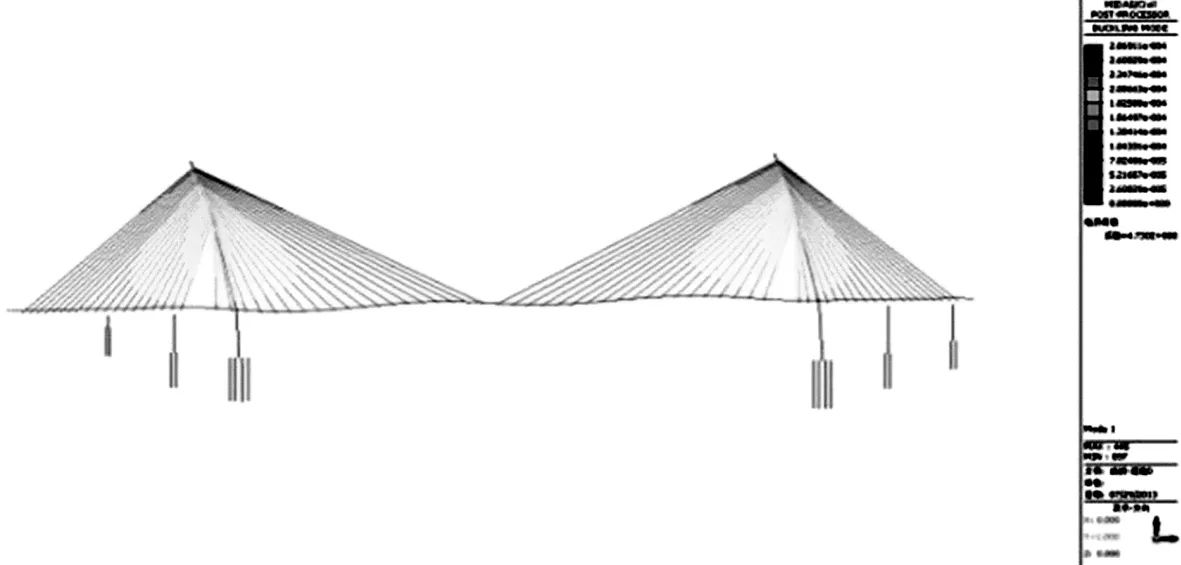
(a)第一阶(主梁的横向一阶)

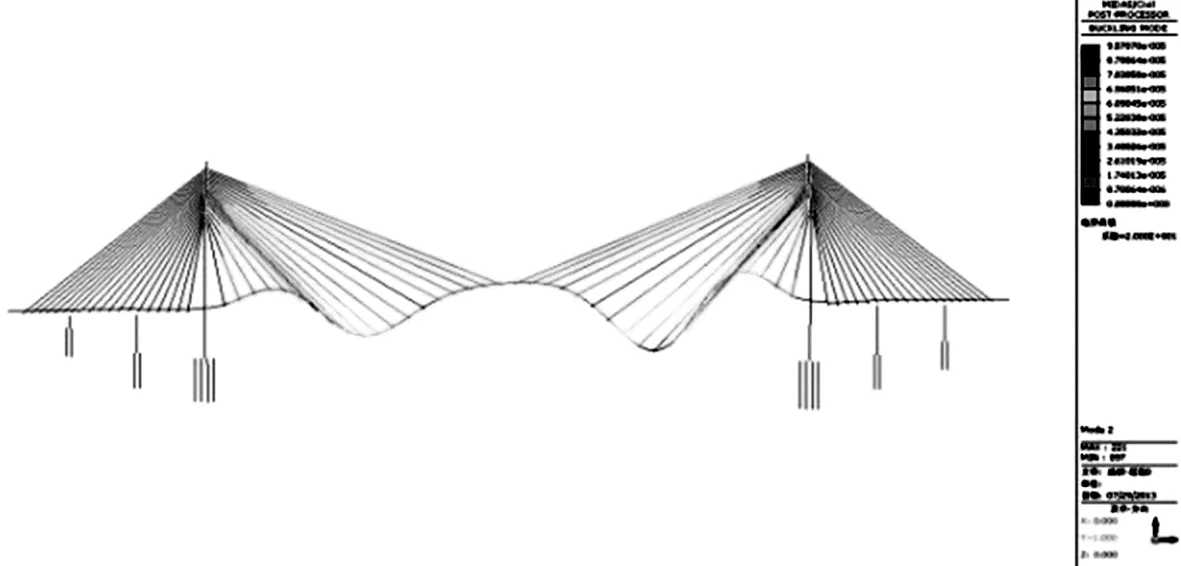
(b)第二阶(主梁的竖向一阶)图3　前两阶失稳模态

3结合段位置的影响

取结合面到塔中心的距离分别为3 m、12 m、22.8 m进行计算，研究结合段的设置位置对位移、内力、自振特性和稳定系数的影响。

3.1结合段位置对位移和内力的影响

选取跨中挠度、塔顶的横向位移、结合面和跨中截面的轴力和弯矩、边跨3#、7#、12#和中跨的9#、11#、14#索的索力为对象，研究结合段位置对位移和内力的影响。表4为不同结合段位置下的位移、内力和索力。由于结合面位置的改变使得结合段两侧梁段的材料和截面特性发生改变，自重荷载的分布也随之改变，为了保证荷载的一致性，将二期恒载作为施加的荷载。

由表4可知，随着结合段的位置越靠近跨中，跨中挠度略有增大，而塔顶的横向位移略有下降，但整体上影响并不大。结合面的轴力和弯矩受结合段位置的影响较大，越靠近跨中设置，结合面的内力越小，对该截面的受力是有利的，而跨中截面的内力受结合段位置的影响不大。由于在二期恒载作用下，部分索受压，表4只给出了拉力较大的索的索力，仍然是靠近结合段的索受结合段位置的影响较大，例如中跨9#索。

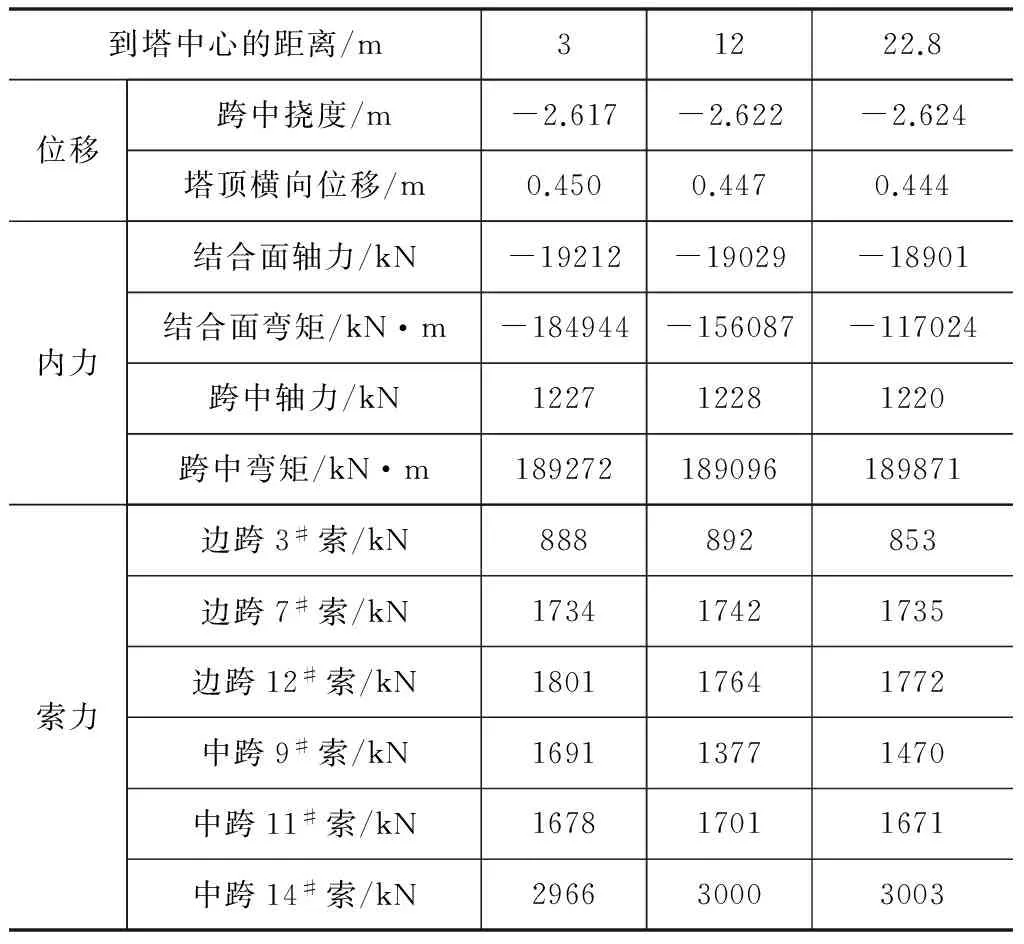
表4　结合段位置对位移和内力的影响

综上所述，结合段位置的改变对结合面的内力和附近索的索力影响较大，而对其他梁段和索力影响很小。

3.2结合段位置对自振特性和稳定系数的影响

表5为不同结合段位置下结构的前8阶频率。

表5　结合段位置对自振频率的影响

由表5可知，结合段位置的改变对低阶频率的影响较大，而对高阶频率影响较小。相对竖弯，结合段位置对横弯模态的影响较大，例如第三阶横弯模态，在结合段距塔中心22.8 m时相对距塔中心3 m时增大了4.7%，表明结合段靠近跨中能够提高主梁的横向刚度。

表6为不同结合段位置下结构的前两阶稳定系数。

表6　结合段刚度对稳定系数的影响

由表6可知，结构的第一阶稳定系数受结合段位置的影响很小，而第二阶稳定系数随着结合段越靠近跨中而略有增大，但整体上影响不大。可见由于结合段的长度相对跨度较小，其对结构整体稳定性的影响可忽略不计。

4结论

通过改变钢-混结合段的刚度和位置，研究其对斜拉桥全桥的位移、内力、自振特性和稳定系数的影响[5]，结果表明：

(1)结合段刚度的改变对结合段附近的梁段和索力影响较大，但对距离结合段较远的梁段和索力影响很小。

(2)结合段刚度的改变对结构整体的自振特性和稳定性影响很小。

(3)结合段位置的改变对结合面的内力和附近索的索力影响较大，而对其他梁段和索力影响很小。

(4)结合段靠近跨中能够提高主梁的横向刚度。

参考文献

[1]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社，2002.

[2]刘应才.大跨度斜拉桥结构计算分析研究[D].西南交通大学,2009.

[3]武利军.基于Midas的斜拉桥索力优化方法与工程实例[J].公路与汽运,2012(5):163-166.

[4]宋雨,陈东霞.斜拉桥动力特性分析[J].厦门大学学报: 自然科学版, 2006,45(1):56-59.

[5]杨万林,刘建军,丁作常.贵州大跨径斜拉桥建设发展与展望[J].公路交通科技:应用技术版, 2015(8).

【中图分类号】U448.27

【文献标志码】A

[定稿日期]2016-03-01