基于CML模型的编队器材携带方案优化方法*

金家善,蔡芝明,陈砚桥

(1. 海军工程大学 舰船动力工程军队重点实验室， 湖北 武汉　430033；2. 海军工程大学 动力工程学院， 湖北 武汉　430033)



基于CML模型的编队器材携带方案优化方法*

金家善1,2,蔡芝明1,2,陈砚桥1,2

(1. 海军工程大学 舰船动力工程军队重点实验室， 湖北 武汉430033；2. 海军工程大学 动力工程学院， 湖北 武汉430033)

摘要：随船备件配置优化问题研究目前主要集中在只有定量或定性约束上，而对既有定性约束又有定量约束的混合约束问题未见文章提及，同时研究对象多为单船，而对舰艇编队研究比较少。针对此问题，以舰艇编队出海任务准备阶段为背景，以保障费用、舰艇仓库空间、舰艇最大排水量及舰员维修能力作为模型的约束条件，以编队备件保障概率为目标函数，采用正态逆向云模型、边际效应法及拉格朗日乘子法(称为CML模型)对此类问题进行求解，给出系统资源因子求解步骤及分析方法，并对本模型进行动态调整和优化。实例分析表明本模型求解方法和步骤可以为多个定量和定性约束下舰船备件携带问题提供新的参考。

关键词：混合约束；编队；备件配置；云模型；边际效应法；拉格朗日乘子法

舰艇编队是现在及未来海军的主流作战样式，其备件携带方案将直接影响任务成功率及战备完好性，在其离码头去执行上级赋予的使命任务之前，必须对其备件携带方案进行优化，达到在满足多个定量或定性约束下保障方案最优及在满足任务要求的前提下最大限度地提高编队系统可用度，同时达到使后勤保障经费降低的目的。

文献[1-2]依据备件领域经典的METRIC理论[3]建立了舰船装备多层级模型；刘勇等[4]以可靠性、质量及经费为约束条件，建立了舰船远航备件存储决策模型；魏曙寰等[5]依据舰艇海上维修器材保障模式，建立了备件携带方案在保障经费及仓库空间约束下的优化模型；费广玉等[6]对随船备件影响因素及指标进行了详细说明，选择满足率作为评价指标；文献[7-8]主要针对航空类装备在经费和重量约束条件下的可用度进行了研究，并建立了相应的模型；阮旻智等[9-10]以经费、备件满足率等为约束条件，对舰载装备维修等级和备件库存模型进行了优化；王乃超等[11]建立了备件保障概率在两个约束因素下的模型，并对库存指标模型进行了优化；文献[12-15]以维修保障能力、虚警、运输时间及保障任务等作为定性约束条件，给出了相应约束条件下的备件最优携带方案和求解步骤。综合分析上述研究成果可以看出：首先，舰船携带备件方案在多个约束作用下，建立相应模型是有一定难度的，故其是研究的热点，同时也必然是难点；其次，目前研究主要集中在只有定性或定量约束问题上，而对既有定量约束又有定性约束的混合约束问题未见文章提及，同时可以看出定量约束问题的解决方法不能应用于定性约束，反之亦不成立，由此可见，寻找一种能够解决混合约束问题的方法的重要性；再次，单舰随船备件携带方案是之前国内外专家研究的主要对象，而把编队作为目标来研究的比较少，未来海军主要作战样式是以舰艇编队为单位进行的，其备件配置方案将直接影响任务成功率及战备完好性；最后，从技术和科学这方面来说，之前文献建立了许多编队备件携带优化模型，但因边际效应法中的边际成本只能为一个定量变量，所以这些模型大部分只针对变量为一个的情况，当变量为多个时，现有技术、模型和方法无法解决此类工程问题。因此，提出用正太逆向云模型将定性约束条件转换为定量约束条件，通过引入约束因素因子，再用拉格朗日乘子法将4个约束因素转换成1个拉格朗日乘子，最后用边际效应法求出最优方案。

舰艇编队备件携带方案需考虑多个定性及定量约束综合权衡得到，常用到的将定性约束条件转换成定量约束条件的方法有：专家打分法[16]、量化加权[17]、层次分析[18]等，这些方法利用不同模型对不确定性进行了研究，优点是：目标明确，边界条件清晰，在研究时分别从模糊性和不确定性两个方面建立模型求解，但二者往往是不能完全分开的。因而，李德毅等建立了云模型[19]，通过相互映射的方法将二者联系到了一起，同时该分析方法已被广泛应用到天气预测[20]、信息技术[21]等领域中。

舰船出海不能无限制地携带维修需要的所有备件，限制因素主要有保障经费、排水量、舰员维修能力和仓库空间，这些因素对舰艇备件携带都具有重要的影响，在建立模型求解的过程中，不能顾此失彼，必须同时考虑，已有模型和方法针对此问题研究比较少，本文以备件费用、质量、体积及维修工时作为约束条件，以备件保障概率作为目标函数，给出了基于CML模型的舰艇编队备件携带方案的优化程序和步骤，最后通过对单个约束条件下的备件携带方案和多个定量及定性约束条件下的备件携带方案进行对比，验证了模型和计算步骤的合理性。

1模型建立

1.1目标函数

舰船备件携带方案和陆地装备主要以后勤保障经费为约束，不同的是，前者还要考虑排水量、仓库空间大小及舰员维修能力，在满足多个约束条件下使其最优，文献[6, 22-25]建立了不同目标函数下的最优备件携带方案，但备件保障概率很少被作为优化对象，上述目标在舰艇编队实际出海备件携带方案制定过程中，管理部门是难以掌控和把握的，因而，本文以编队备件保障概率Ps为目标函数。船上电子设备累计概率密度函数都服从指数分布，计算每项备件保障概率Pi是一样的，即：

(1)

式中：i(i=0,1,2,…,I)为备件编号；j(j=0,1,…,J)为第i项元器件的备件需求量；Ni为第i项电子元件单机安装数；λi为第i项元器件故障率；ti为第i项备件供应周期。

舰艇装备主要由两个层级组成，即舰船现场可更换或拆卸单元(Line-Replaceable Unit， LRU)和车间可更换或拆卸单元(Shop-Replaceable Unit， SRU)，LRUi年平均故障率λi为：

(2)

式中：DCi为占空比；RIPi为故障件可以在故障现场修理的概率；T0为装备年平均工作时间；L为随船装备配置数量；MTBFi为部件i的平均故障间隔时间；RtOKi为部件i的重测完好率。依据故障树分析原理，母体的需求率是由其各个分部件SRUk(k∈sub(i))的需求率所引起的，若装备LRUi发生故障是由其组成部件引起的概率为Pik，则SRUk的需求率(故障率)λk为：

λk=λi·Pik

(3)

(4)

把式(4)代入式(3)得：

(5)

第y(y=1,2,…,Y)条船备件保障概率psy为：

psy=pscy·psdy

(6)

式中：pscy为修理所需求的备件放在故障现场的概率；psdy为假设在事先设定的约束条件下，需求的备件放在故障现场且可以获得的概率。其计算方法为：

(7)

(8)

式中，λTy为第y船总故障率，且

(9)

根据式(6)～(9)，按上述给定的计算步骤和方法可得到第y船的保障概率Psy，即：

(10)

编队舰艇在海上彼此之间的距离远比离岸上保障基地距离要近的多，因而可将编队看成一个整体系统，舰船修理车间不进行串件拼修的前提下，舰艇编队备件保障概率依据式(10)并考虑一些其他修理因素综合权衡分析可得到，即：

(11)

其中：

(12)

此时，目标函数为:

maxPs

(13)

1.2约束条件

舰船备件携带问题可以理解为在多个定量和定性影响因素下，综合考虑各种维修因素，通过携带不同种类和数量的备件，使舰艇编队Ps达到最优。

舰艇仓库携带的所有备件体积之和必须小于舰艇仓库空间所能承受的上限，即:

(14)

式中:viy为备件LRU，SRU的体积；Vt为舰艇编队仓库空间所能承受的上限值。

虽然与仓库体积及排水量相比，保障经费并非刚性约束，即以费用最小化和保障概率最大化共同作为优化目标更为实际，但为简化问题，本文将其作为约束因素，编队出海购买所有备件的费用总和必须小于保障经费的上限，即：

(15)

式中：ciy为单件LRU,SRU的费用；Ct为决策者所能给予的保障经费的最大值。

编队携带备件所有重量之和必须小于舰船载荷所能承受最大值的上限，即：

(16)

式中：miy为单件LRU，SRU的质量；Mt为事先给定的仓库质量指标。

维修能力对于舰船的重要性是显而易见的[6,14-15,23]。标准工时[26]：在规定的工作环境里，按规定的流程，以标准工作者正常速度完成装备修理所必要的时间。编队舰员更换及调试装备所需的维修工时之和必须小于所有维修人员所能承受的最大值，即：

(17)

式中：wiy为第y条船的第i个备件从拆卸开始到测试结束所需要的维修工时；Wt为编队舰员所能承受维修工时的最大值；w′y为第y船上单位时间内所具有的平均维修保障能力；Ty为任务周期。

1.3模型的建立

编队离码头执行上级下达的某项具体任务之前，决策者要综合影响备件携带的所有因素，在满足各种因素所能承受值的最大值的前提下，求出编队备件保障概率Ps最优值，所建模型如下：

(18)

2模型求解方法

2.1正态云模型的引入

目前将定性转换成定量的方法有很多，如专家打分法、模糊层次分析法等[16-18]，其包含着一些数学方法和计算模型，但上述方法并没有将研究对象的模糊性和随机性很好地统一起来[19]，因而李德毅建立了定性条件和定量条件转换模型，并给出了其求解步骤和程序，通过构建二者之间的映射关系，将定性和定量之间的信息进行处理，达到相互转化的目的。

定义1[27]正态分布通常用均值和方差两个特征值来表示；模糊理论中用的最多的是钟形隶属度函数，通常用

(19)

来定义，正态云模型是以两者为基础发展而来的一种新的模型。

定义2[27]设U是一个由很多精确数值确定的定量论域，C属于U的定性概念表现，若确定的数量值x∈U，且x是定性概念C的一次随机实现，若x满足：

x～N(Ex,En′2)

(20)

其中

En′～N(En,He2)

(21)

且x对C的确定度满足：

(22)

则x在论域U上的分布称为正态云。

定义3设U是维修能力T用精确数值给定的定量论域，X⊆U，T是U空间上的关于维修能力的定性概念，若对于维修工时x(x∈X)都存在一个稳定倾向的随机数CT(x)∈[0,1]，称为维修工时x对维修能力T的隶属度，即：

CT(x):U→[0,1],∀x∈X(X⊆U),x→CT(x)

(23)

无论在自然科学还是其他学科(如社会科学)都已经论证了李德毅所给出的正态云模型的科学性、合理性及普适性[27]。

一个云滴就是云模型中一次定性的随机实现，云模型中云滴是无限的，但其取值并不是绝对或连续的无限，文中处理的维修工时就是一次维修能力的定性实现，当得到多个维修工时云滴，便得到了装备的维修能力；常规意义上的定性概念(如高、中、低等)是有限取值和具体离散的值。从以上两个方面可以看出，二者相互联系但也有客观上的区别，这些不同决定了云模型中的定性概念和常规意义上的定性概念有本质区别。

2.2基于正态逆向云模型的定性与定量变量转换模型

从文献[27]给出的正态云模型可以看出，用该方法来还原云模型中的数字特征，更加符合舰船备件携带工程方面的要求，易于推广到高维逆向云模型中去，该方法是以统计原理为基础的，在实际计算过程中，不同的样本值有可能引起少量的误差，主要体现在计算超熵He时，容易出现超熵值为虚数的情况，若出现超熵值为虚数，则说明本次求解过程失败，需要选择新的云模型重新计算，为此，对算法进行了改进，对差值取绝对值并加上了控制参数，提高了计算的鲁棒性，减小了计算误差。算法具体计算步骤如下：

步骤1：输入第i个备件R个云滴样本的数字值xir(r=1,2,…,R);

步骤2：依据R个云滴数字值xir可求解出均值大小：

(24)

步骤3：计算样本期望：

(25)

步骤4：计算样本熵：

(26)

步骤5：计算R个样本云滴方差：

(27)

步骤6：计算样本超熵：

(28)

式中，Ci为控制参数，一般情况下取值为1，可对超熵进行适当调节，使其处于一个管理者可接受的合理范围。

步骤7：重复步骤1～6共I次，得到所有备件云模型的特征参数。

2.3模型的求解方法

由于涉及的约束变量为定性1个和定量3个，而边际效应法求解的原理是用边际效益除以边际成本得到边际效益值，通过逐次比较边际效益值的大小，从而确定编队携带备件的种类和数量，但边际效应法要求边际成本必须为一个定量变量，因而，一方面需要寻找一种可以将定性变量变成定量变量的方法，另一方面需要寻找将4个定量变量变成1个定量变量的方法，最后，用边际分析法求解得到编队库存备件最合理的携带方案。

用云模型将定性变量转换为定量变量，具体见2.1和2.2节，此方法求得的定量值可以作为拉格朗日乘子输入值；单纯拉格朗日乘子法主要思路是引入新的参数 进而求出极值解，本文主要是借用该数学方法的思想，引入4个变量因子，用拉格朗日乘子法将4个定量变量转换为1个定量变量(一个备件对应一个定量值)，文献[9,11]已验证了本文所用方法的正确性；最后，将备件定量值作为边际成本变量输入到边际效应方法中，求出编队最优备件携带方案，下面是该方法的具体求解步骤。

步骤1：从式(11)和式(18)可以看出，舰艇编队备件携带问题的影响因素有很多，需要将这些因素(舰艇载荷大小、备件体积、经费及舰员维修能力)统一转化为zi，即：

zi=λmmi+λvvi+λcci+λwwi

(29)

式中：zi为单元i的系统保障资源约束因子；λm为质量因子；λv为体积因子；λc为费用因子；λw为舰员维修能力因子。

步骤2：将备件的3个定量因素和1个定性约束因素，依据式(29)转化为系统资源约束Zi后，在其基础之上运用适当的数学变换，即可求出编队Ps，即：

(30)

步骤3：依据凸函数叠加之后仍然是凸函数的原理，依据式(29)及文中给的程序和步骤重复计算I次，可得到当前系统约束组合为：

zt=(z1,z2,…，zi，…,zI)

(31)

步骤4：对式(31)做一阶差分，即：

ΔPzi(si)=Pzi(si+1)-Pzi(si)

(32)

步骤5：将式(31)除以式(32)，即：

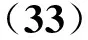
对Δ矩阵按边际效应分析法进行处理，逐次选择最大值，如此进行多次循环，当所有影响因素不再满足指标上限时停止。

步骤6：循环步骤4～5，直到携带备件种类和数量不能再增加时停止。

3初始约束因子的确定及动态调整

在求解得到备件综合资源约束Zi之前，必须先求出舰船备件配置初始方案，从而确定舰船载荷因子λm、舰船仓库空间因子λv、费用因子λc、维修因子λw的初值，记初始舰船载荷因子为λm0，初始仓库空间因子为λv0，初始维修因子为λw0，模型求解方法和优化步骤如下：

步骤1：当舰艇仓库空间、舰艇载荷及舰员维修能力不被作为约束条件时，通过费效曲线计算得到一组初始备件携带方案，即：

sc0=(s01j,s02j,…,s0ij,…,s0Ij)

(34)

步骤2：舰艇载荷、维修工时、保障经费及舰艇仓库空间都可在式(34)的基础上，运用文中模型给的步骤和程序求出，然后用两两之间的相互比值λcm0，λcv0，λcw0作为初始因子，即：

(35)

(36)

(37)

步骤3：将式(35)～(37)值代入式(29)，即：

zc0ij=cij+λcv0vij+λcm0mij+λcw0wij

(38)

步骤4：依据式(33)和式(38)按文中给定步骤再次求解备件携带方案，即：

sc1=(sc11j,sc12j,…,sc1ij,…,sc1Ij)

(39)

步骤5：在计算过程中可能会出现一种情况，计算得到总的备件质量、仓库体积和保障费用超过了指标最大值上限，需要对初始各种约束条件影响因子进行适当变换，即：

(40)

(41)

(42)

步骤6：依据式(40)～(42)对约束条件因子进行适当处理之后，绝大部分时候都会满足约束条件指标要求，但还有可能出现一种情况：无论怎么调整备件因子值的大小，求出的备件携带方案都不能满足所有约束指标的要求，总会有1个或多个指标不满足要求。此时，需要调整约束指标上限值，可增加舰艇载荷所能承受的指标M、舰船仓库所能承受指标V、维修人员能承受最大工作工时指标W或者舰船保障经费指标C。

依据第2节和本节内容，可以得出CML模型计算的流程如图1所示。

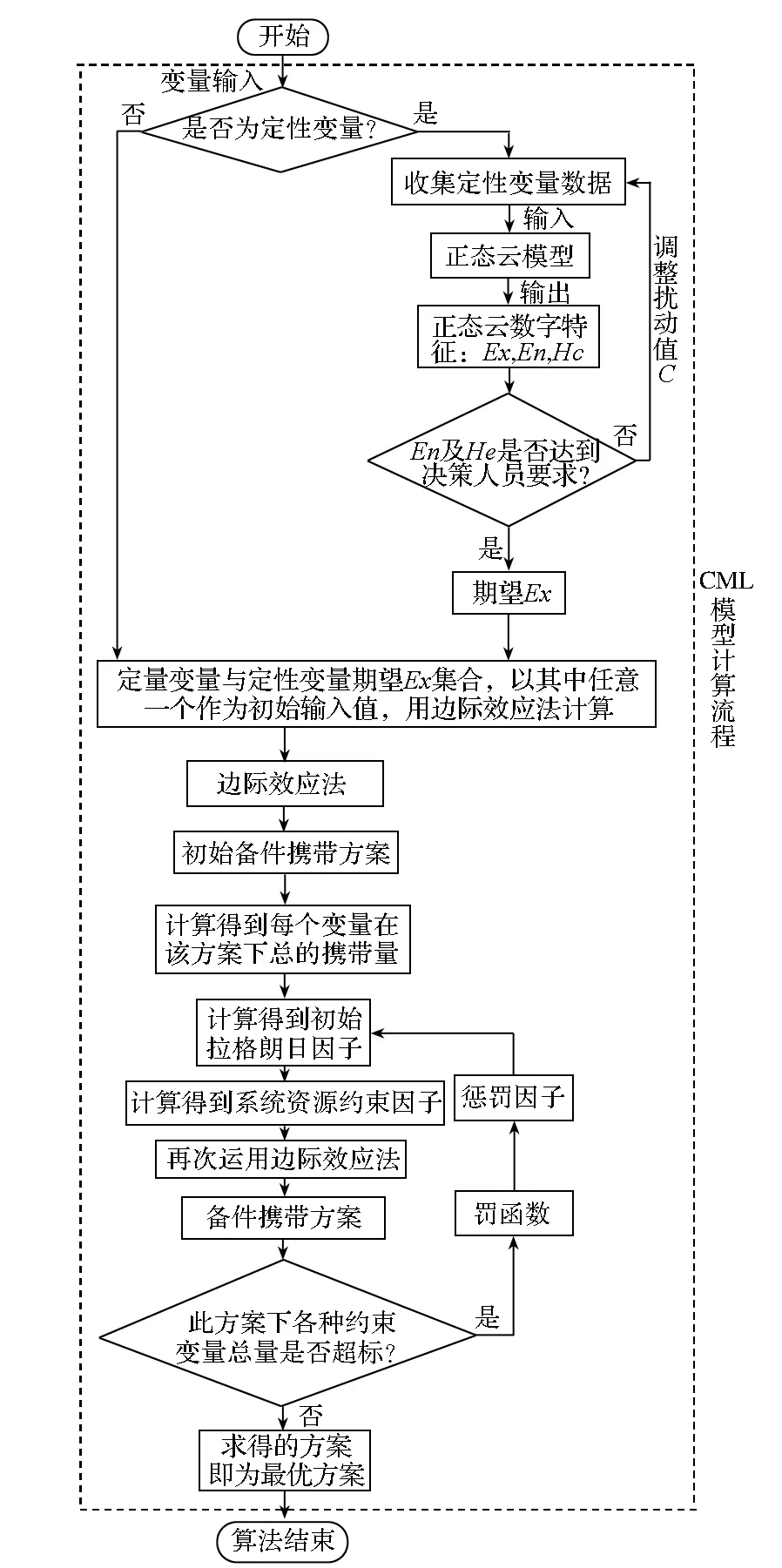
图1　CML模型流程图Fig.1　Flow chart of CML model

4案例分析

3艘最新型舰船准备出海去完成上级赋予的使命任务，离码头之前需要综合权衡保障经费、维修能力、仓库空间及排水量等约束条件，使保障方案在满足所有约束条件前提下最优。由于舰船装备种类和数量繁多不能一一列举，同时本文重点在于建立编队备件方案求解模型，并给出模型优化步骤，因此，表1只给出了会给舰艇航行带来致命性影响的一些重要装备，并对属性值进行了适当处理，其他装备求解

过程和计算流程是一样的。

按照文献[27]中关于维修工时的标准，去该类舰船进行调研，依据装备维修工作记录本等资料获取这10个备件维修所需工时，具体见表2。

按文中2.2节给定的计算步骤，得到10个备件的三个特征参数，并据此得出10个备件的云分布图，云滴分布符合决策人员要求的标准，具体见表3。依据表1～3的数据，按2.3节给定的模型求解方法及第3节模型优化方法，求解得到不同影响因素下对应的保障方案，具体见表4。

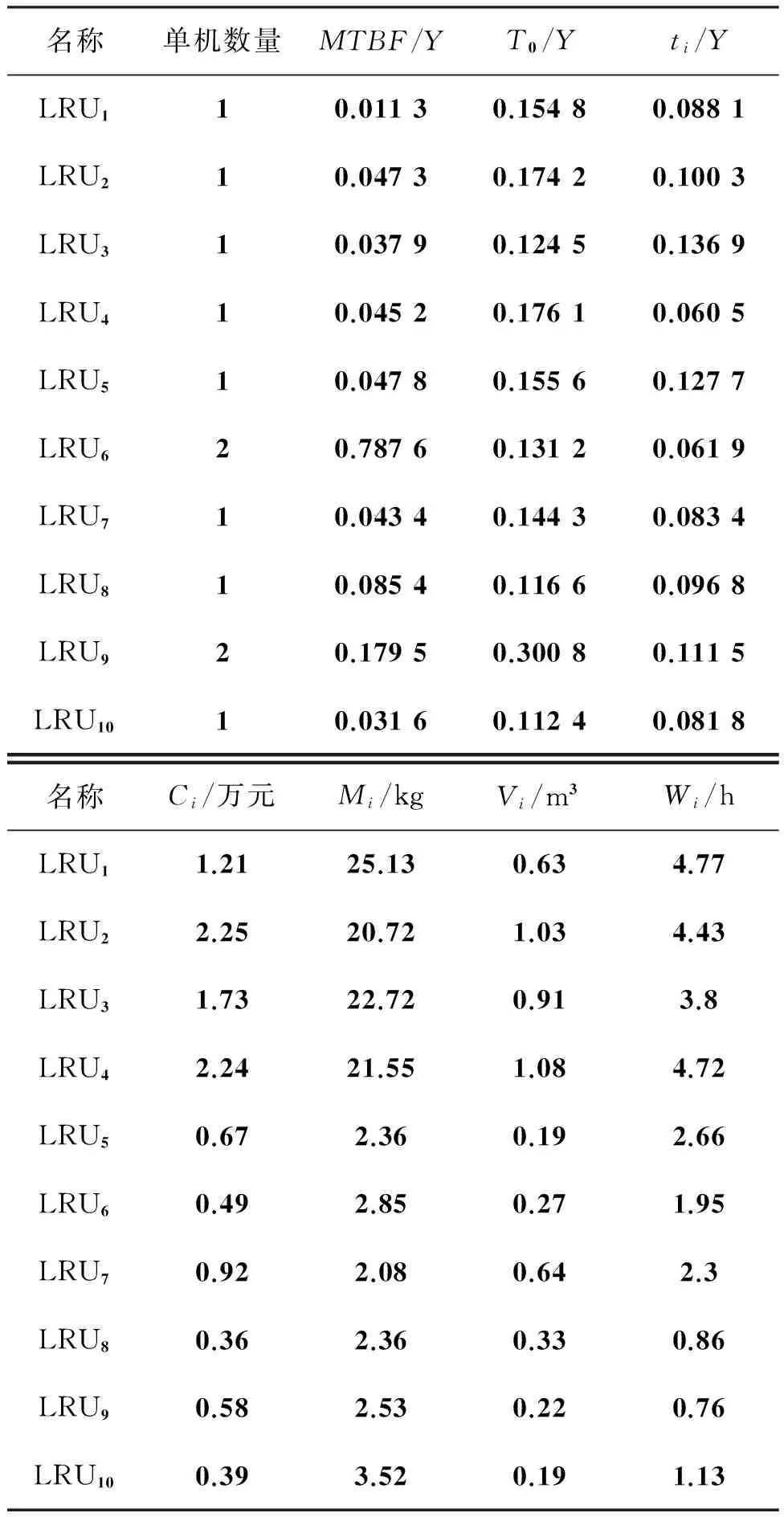
表1　备件属性表

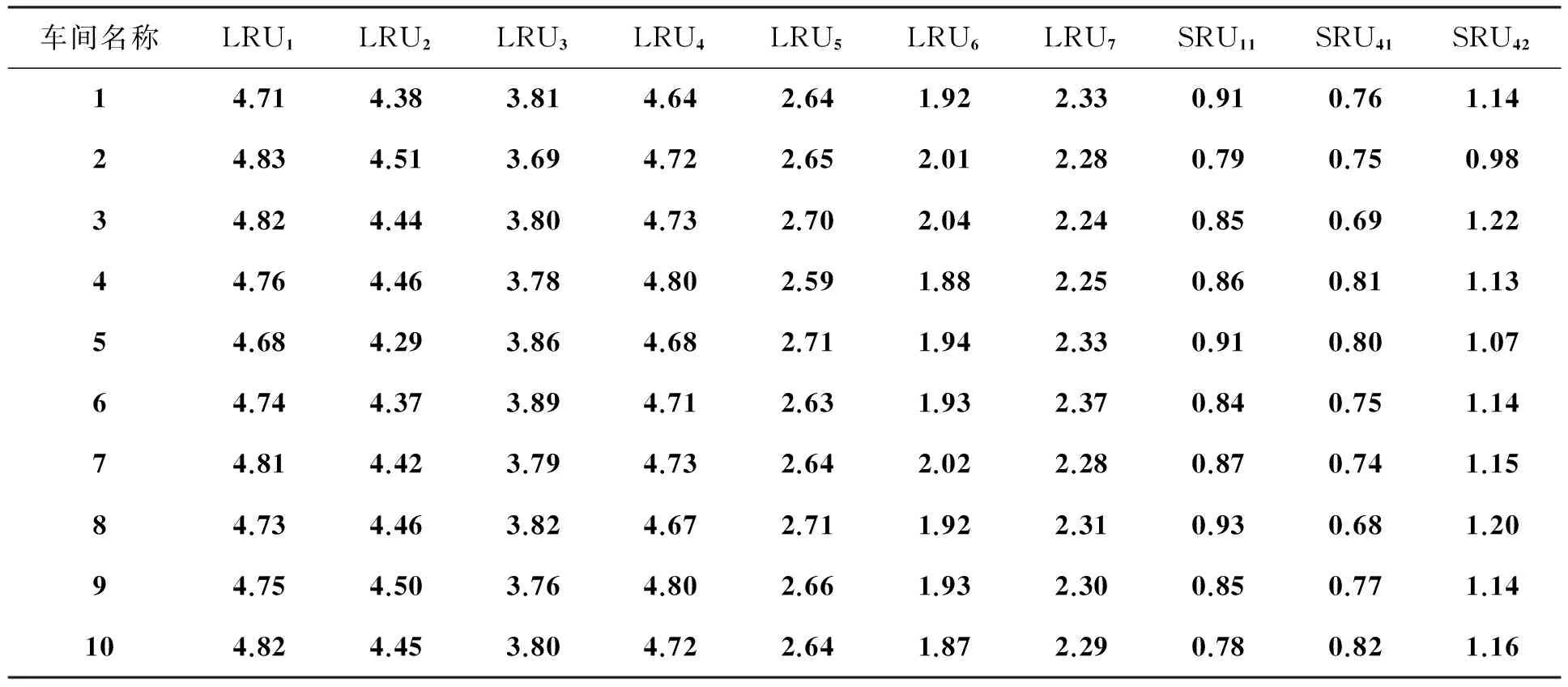
表2　备件维修工时表

表3　备件云模型数字特征

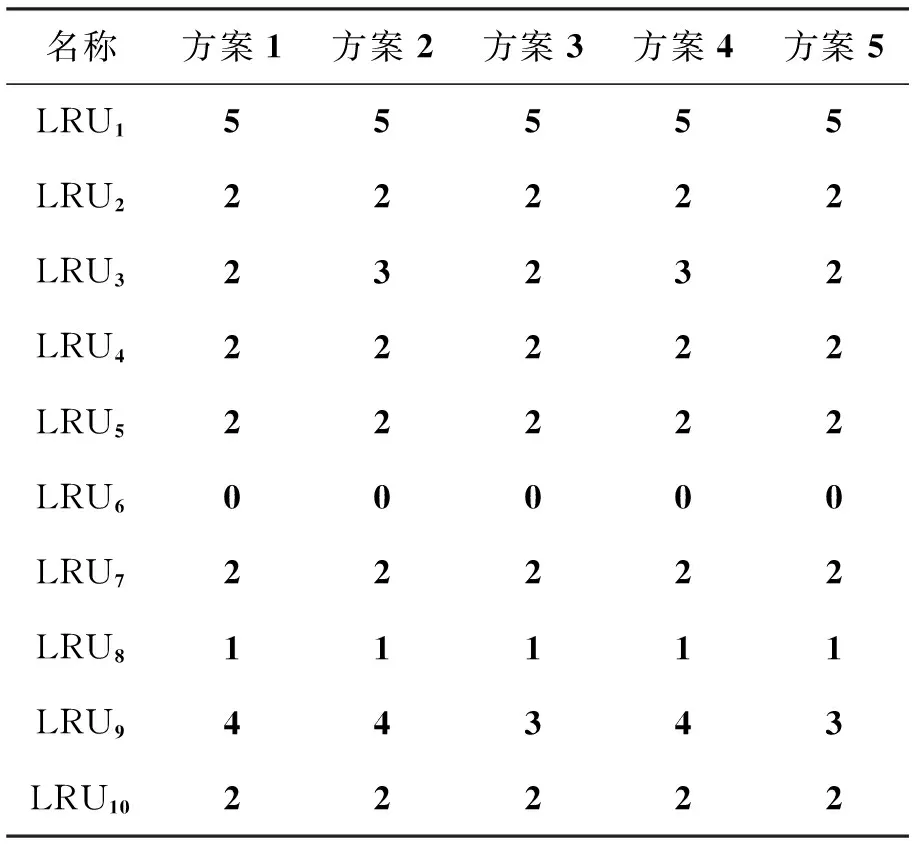
表4　不同约束条件下编队随船备件携带方案

舰艇编队给定的保障经费最大值为25.2万元，载重最大值为307 kg，仓库最大体积为13.5 m3，维修工时指标为65.1 h。依据表4的结果可以计算推导出表5，从表5的5个可行性方案可以看出，只有方案3和方案5的各项约束值均满足给定的影响因素所能承受最大值上限的要求，方案1、方案2和方案4分别有指标超过了给定指标，均不满足要求。

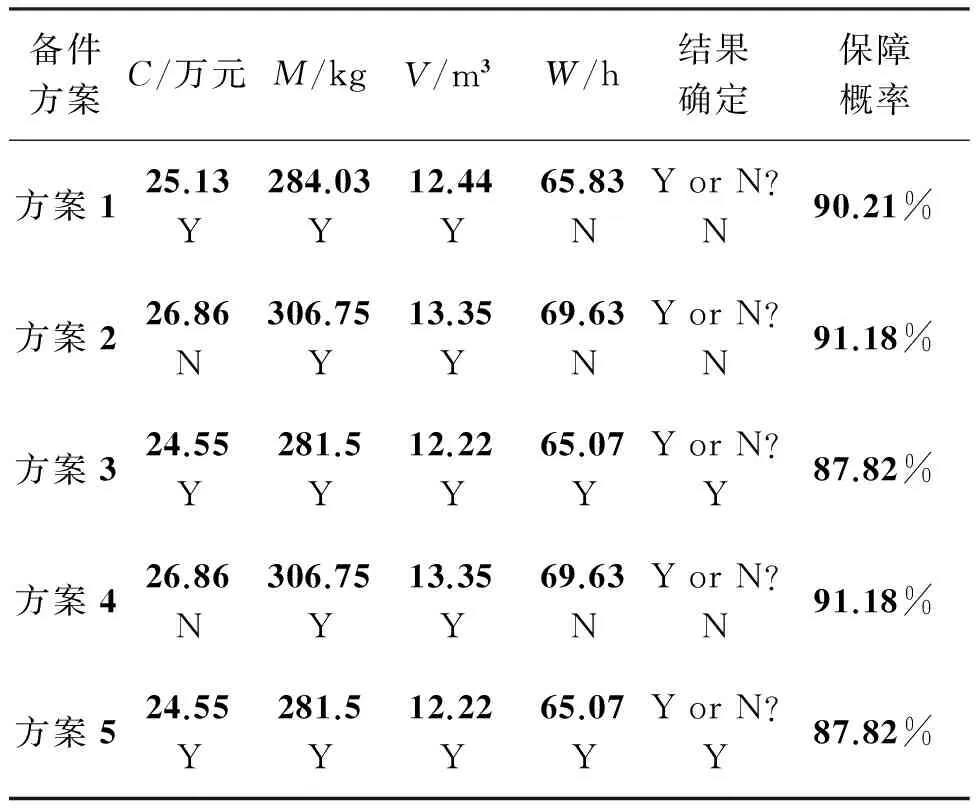
表5　不同约束下编队随船备件携带方案结果

从表5可以看出：

1)方案1，2和4因其都是将一个影响因素作为约束条件，求出的备件最优配置方案都不满足所有约束因素的要求，从上面可以看出随船备件配置必须考虑所有的影响因素，此时求出的才是符合所有约束因素要求的最优方案。

2) 一方面，综合考虑编队所有影响因素，按文中模型计算得到的备件携带方案，满足所有约束条件且是最优方案；另一方面，只考虑编队一个影响因素，按边际效应法计算得到的备件携带方案，是否能满足所有约束条件是偶然的，因此，这也从另一角度证明了本文研究的必要性。

3) 已有研究方法主要侧重对单船或陆地装备进行研究，取得了很多成果，但这些方法无法科学、合理地解决舰艇编队备件携带方案的制定问题，故提出CML模型和方法，通过和已有方法将编队中的舰艇分开来研究的情况进行对比，证明了本文方法在提高装备战备完好性的同时，可以有效降低保障经费。

不同约束下的舰艇编队最优保障曲线如图2～6所示。

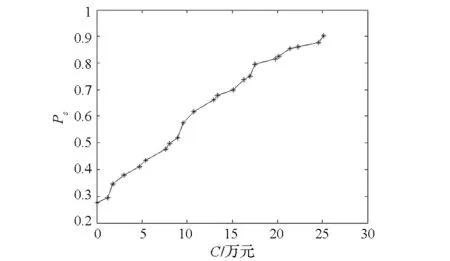
图2　费用约束下的最优Ps曲线Fig.2　Optimal curve of support probability under cost constraints

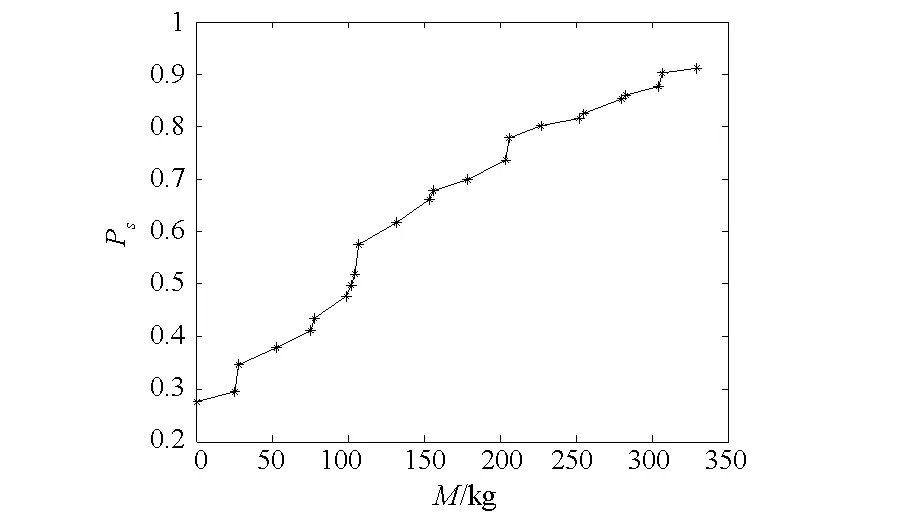
图3　质量约束下的最优Ps曲线Fig.3　Optimal curve of support probability under mass constraints

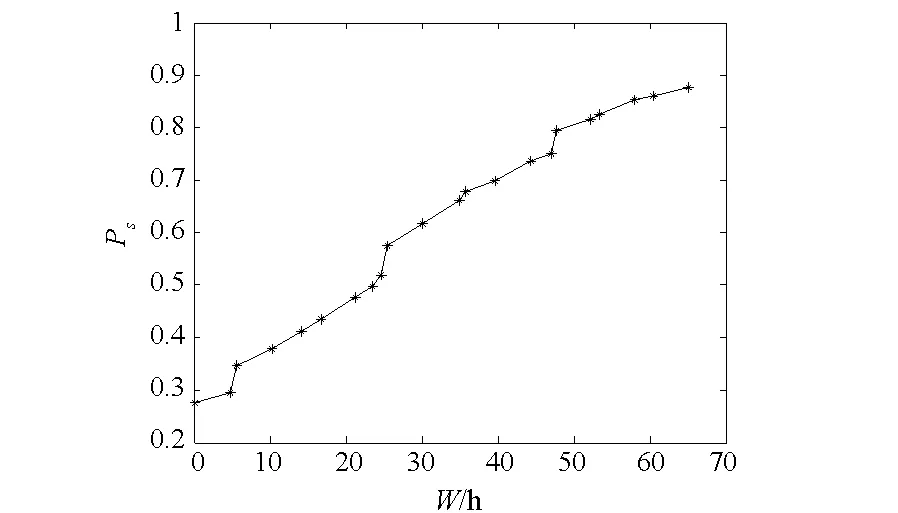
图4　维修能力约束下的最优Ps曲线Fig.4　Optimal curve of support probability under maintenance per hour constraints

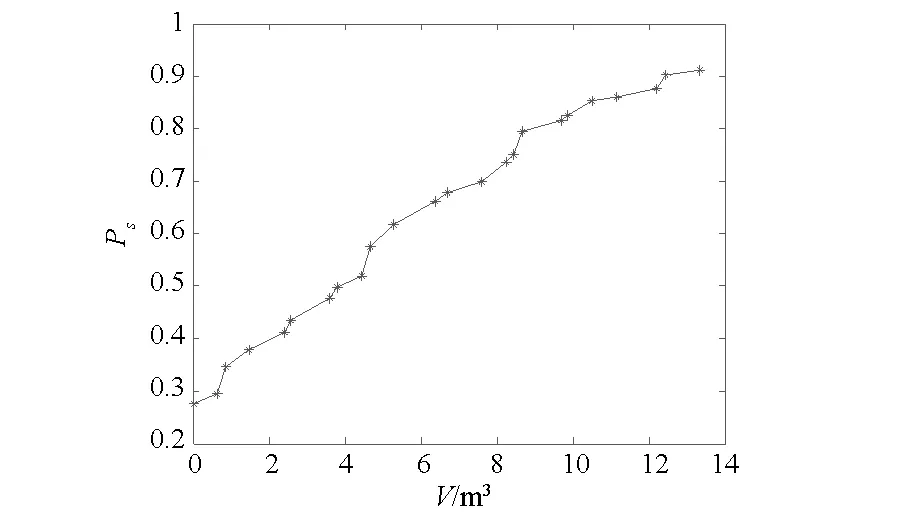
图5　体积约束下的最优Ps曲线Fig.5　Optimal curve of support probability under volume constraints

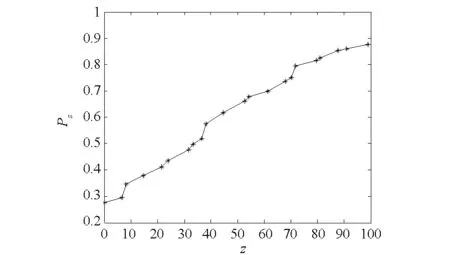
图6　混合约束下的最优Ps曲线Fig.6　Optimal curve of support probability under mix-constraints

综合分析约束因素下的最优Ps曲线，可以得到：

1)随船备件配置方案不仅受备件种类和数量的影响，同时也受其各种指标条件约束。根据不同因素条件，运用文中给定的模型求解得出不同优化曲线；

2)方案制定者依据最优Ps曲线，可以制定编队出海之前在相应影响因素下的最优备件携带种类和数量。例如，以图5中点(9.68，0.817 4)为例进行说明，当编队Ps达到81.74%时，所有备件体积之和为9.68 m3，因此，设定的体积最小指标值必须达到Vt≥9.68 m3，若给定的体积指标小于9.68 m3时，相应地应该通过适当降低Ps来达到满足约束条件上限要求；

3)上述影响因素和最优Ps在约束条件和目标函数之间是可以相互转换的，可根据具体工程决策者的要求具体分析。

5结论

主要针对编队随船备件配置方案中既有定量约束又有定性约束的混合问题进行了研究。可以为解决多个定量及定性约束的混合问题提供借鉴，当约束条件增加时，只要对模型系统资源约束因子适当调整即可，计算流程不变，模型的适用性比较强。模型可以有效克服主观方法的不足，同时兼顾复杂系统的随机性和模糊性。建立的模型、求解方法及优化程序对舰船备件携带有重要参考价值，而且对于其他复杂系统领域装备等同样具有一定的参考意义。一方面，编队的组成形式主要取决于任务样式，任务不同组成形式不同，但求解过程和用到的模型及方法是相似的；另一方面，若编队(有2艘或以上舰船即可组成编队)中舰艇数量随着实际情况有变化(假设有Z艘且Z>3)，舰船数量的增加将主要是增加计算工作量，而用到的模型和方法都是相同的。

随船备件配置方案不仅与备件种类和数量有关，还与任务强度及仓库地理位置等相关，同时本文并未考虑舰艇编队内部备件的串件拼修，这部分内容将是接下来研究的重点。

参考文献(References)

[1]Sleptchenko A, Van der Heijden M C, Van Harten A. Effects of finite repair capacity in multi-echelon, multi-indenture service part supply systems[J]. International Journal of Production Economics, 2002, 79(3): 209-230.

[2]Rustenburg W D, Van Houtum G J, Zijm W H M. Spare parts management at complex technology-based organizations: an agenda for research[J]. International Journal of Production Economics, 2001, 71(1/2/3): 177-193.

[3]Sherbrooke C C. METRIC: a multi-echelon technique for recoverable item control[J]. Operations Research, 1968, 16(1): 122-141.

[4]刘勇, 盖强, 赵翀, 等. 多约束下舰船远航备件储量决策[J]. 舰船科学技术, 2013, 35(11): 144-147.

LIU Yong, GAI Qiang, ZHAO Chong, et al. Research on spare parts storage decision for ships on sailing in multi-restrain[J].Ship Science and Technology, 2013, 35(11): 144-147. (in Chinese)

[5]魏曙寰, 陈砚桥, 金家善. 空间和费用约束条件下的随船备件配置优化方法[J]. 系统工程与电子技术, 2013, 35(12): 2540-2544.

WEI Shuhuan, CHEN Yanqiao, JIN Jiashan. Warship spare parts allotment method under space and cost constraints[J]. Systems Engineering and Electronics, 2013, 35(12): 2540-2544. (in Chinese)

[6]费广玉, 张志华, 刘军, 等. 舰船随舰备件配置方法[J]. 指挥控制与仿真, 2014, 36(3): 133-136.

FEI Guangyu, ZHANG Zhihua, LIU Jun, et al. Configuration method of spares on warship[J]. Command Control & Simulation, 2014, 36(3): 133-136. (in Chinese)

[7]Lee L H, Chew E P, Teng S, et al. Multi-objective simulation based evolutionary algorithm for an aircraft spare parts allocation problem[J]. European Journal of Operational Research, 2008, 189(2): 476-491.

[8]Kline R C, Bachman T C. Estimating spare parts requirements with commonality and redundancy[J]. Journal of Spacecraft and Rockets, 2007, 44(4): 977-984.

[9]阮旻智, 李庆民, 张光宇, 等. 多约束下舰船装备携行备件保障方案优化方法[J]. 兵工学报, 2013, 34(9): 1144-1149.

RUAN Minzhi, LI Qingmin, ZHANG Guangyu, et al.Optimization method of carrying spare parts warship equipment under multi-constraints[J]. Acta Armamentarii, 2013, 34(9): 1144-1149. (in Chinese)

[10]阮旻智, 李庆民, 彭英武, 等. 多指标约束下舰载装备维修级别建模与优化[J]. 系统工程与电子技术, 2012, 34(5): 955-960.

RUAN Minzhi, LI Qingmin, PENG Yingwu, et al. Modeling and optimization for repair level of shipborne equipment under multi-constraints[J]. Systems Engineering and Electronics, 2012, 34(5): 955-960. (in Chinese)

[11]王乃超, 康锐. 多约束条件下备件库存优化模型及分解算法[J]. 兵工学报, 2009, 30(2): 247-251.

WANG Naichao， KANG Rui. An optimization model for inventory spares under multi-constraints and its decomposition algorithm[J]. Acta Armamentarii, 2009, 30(2): 247-251.(in Chinese)

[12]卞洁辉, 郭霖瀚, 康锐, 等. 虚警影响下的备件库存优化[J]. 北京航空航天大学学报, 2014, 40(3): 1-4.

BIAN Jiehui, GUO Linhan, KANG Rui, et al. Spares optimization under the influence of false alarm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(3): 1-4. (in Chinese)

[13]徐立, 李庆民, 阮旻智. 具备有限维修能力的舰船编队保障方案优化 [J]. 系统工程与电子技术, 2014, 36(11): 2226-2232.

XU Li, LI Qingmin, RUAN Minzhi. Support project optimization for warship formation with finite repair capacity[J]. Systems Engineering and Electronics, 2014, 36(11): 2226-2232. (in Chinese)

[14]王正元, 曹继平, 朱昱, 等. 考虑维修能力的战时备件资源配置方法研究[J]. 兵工学报, 2014, 35(5): 719-724.

WANG Zhengyuan,CAO Jiping,ZHU Yu, et al. An optimization model of wartime spare parts resource allocation on consideration of maintainability[J]. Acta Armamentarii, 2014, 35(5): 719-724. (in Chinese)

[15]王正元, 曹继平, 朱亚红, 等. 可移动备件仓库设置优化方法[J]. 系统工程与电子技术, 2013, 35(11): 2352-2355.

WANG Zhengyuan,CAO Jiping, ZHU Yahong, et al. Optimization model on removable spare parts warehouse deployment[J]. Systems Engineering and Electronics, 2013, 35(11): 2352-2355. (in Chinese)

[16]郭海鹏, 黄胜, 王超. 基于改进德尔菲法的舰船总体方案群决策方法[J]. 上海交通大学学报, 2014, 48(4): 13.

GUO Haipeng, HUANG Sheng, WANG Chao. Group decision-making method of warship overall scheme based on improved Delphi[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 13. (in Chinese)

[17]蔡坦, 刘卫宁, 刘波. 一种新的基于直觉模糊集的制造云服务优选方法[J]. 中国机械工程, 2014, 25(3): 352-356.

CAI Tan，LIU Weining，LIU Bo. A new method of cloud manufacturing service optimal-selection based on intuitionistic fuzzy set[J]. Chinese Journal of Mechanical Engineering, 2014, 25(3): 352-356. (in Chinese)

[18]杨兆军, 王继利, 李国发, 等. 冲压机床可靠性增长的模糊层次分析预测方法[J]. 吉林大学学报: 工学版, 2014，44(3): 686-691.

YANG Zhaojun, WANG Jili, LI Guofa, et al. Reliability growth prediction based on fuzzy analytical hierarchy process for punching machines[J]. Journal of University (Engineering and Technology Edition), 2014， 44(3): 686-691. (in Chinese)

[19]李德毅, 孟海军. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995, 32(6): 15-20.

LI Deyi, MENG Haijun. Membership cloud and membership cloud generators[J]. Journal of Computer Research and Development, 1995, 32(6): 15-20. (in Chinese)

[20]Farley R D, Nguyen P, Orville H D. Numerical simulation of cloud seeding using a three-dimensional cloud model[J]. The Journal of Weather Modification, 2014, 26(1): 113-124.

[21]Rezaei R, Chiew T K, Lee S P, et al. Interoperability evaluation models: a systematic review[J]. Computers in Industry, 2014, 65(1): 1-23.

[22]Molenaers A, Baets H, Pintelon L, et al. Criticality classification of spare parts: a case study[J]. International Journal of Production Economics, 2012, 140(2): 570-578.

[23]Romeijnders W, Teunter R, Van Jaarsveld W. A two-step method for forecasting spare parts demand using information on component repairs [J]. European Journal of Operational Research, 2012, 220(2): 386-393.

[24]Costantino F, Di Gravio G, Tronci M. Multi-echelon, multi-indenture spare parts inventory control subject to system availability and budget constraints[J]. Reliability Engineering & System Safety, 2013, 119: 95-101.

[25]Caglar D, Li C L, Simchi-levi D. Two-echelon spare parts inventory system subject to a service constraint[J]. IIE Transactions, 2004, 36(7): 655-666.

[26]张峰, 殷秀清. 基于产品批量生产的标准工时测量[J]. 山东理工大学学报 (自然科学版), 2014, 28(3): 56-59.

ZHANG Feng, YIN Xiuqing. The standard time measurement based on product batch production[J]. Journal of Shangdong University of Technology(Natural Science Edition), 2014, 28(3): 56-59. (in Chinese)

[27]李德毅, 刘常昱. 论正态云模型的普适性[J]. 中国工程科学, 2004, 6(8): 28-34.

LI Deyi, LIU Changyu. Study on the universality of the normal cloud model[J]. Engineering Science, 2004, 6(8): 28-34. (in Chinese)

doi:10.11887/j.cn.201602022

*收稿日期：2015-03-12

基金项目：国家部委基金资助项目(51319060103)；中国博士后科学基金资助项目(2013T60921)

作者简介：金家善(1962—)，男，山东青岛人，教授，博士，博士生导师，E-mail：jinjiashan401@163.com

中图分类号：TJ83; U662.1

文献标志码：A

文章编号：1001-2486(2016)02-128-10

Optimization method of carrying maintenance material support project for warship formation based on CML model

JIN Jiashan1,2, CAI Zhiming1,2, CHEN Yanqiao1,2

(1. Military Key Laboratory for Naval Ship Power Engineering, Naval University of Engineering, Wuhan 430033, China；2. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China)

Abstract：At present, studies in spares allotment optimization area mainly focus on the conditions that there is only qualitative or quantitative constraint. Nevertheless, the mix-conditions have not been reported to the best of our knowledge from the literatures. The researches usually concern the single warship, but fewer show concern about the warship formation. In view of this problem, the mission preparation of warship formation before sailing was taken as a research background; the warship formation support cost, warship storage space, warship carrying ability and crew maintenance ability were adopted as the mixed-constraints conditions; the spare parts support probability was served as the objective function. A normal reverse distribution cloud model, the marginal effect and the Lagrange multiplier methods (CML model) were used to solve such warship formation spare parts allotment problem. A method was proposed for the determination and dynamical updating of system resource constraint factors, meanwhile, the selecting methods and calculating process of the model was optimized. The reliability of the method which can provide a new trial for the problem of warship formation spare parts allotment under the mixed constraints condition was proved by an actual case.

Key words：mixed-conditions; warship formations; spares allotment; cloud model; marginal effect method; Lagrange multiplier method

http://journal.nudt.edu.cn