高精度有限体积格式在三维曲线坐标系下的应用*

徐　丹，王东方，陈亚铭，邓小刚

(1.国防科技大学 航天科学与工程学院， 湖南 长沙　410073； 2.国防科技大学 理学院， 湖南 长沙　410073)



高精度有限体积格式在三维曲线坐标系下的应用*

徐丹1，王东方1，陈亚铭2，邓小刚1

(1.国防科技大学 航天科学与工程学院， 湖南 长沙410073； 2.国防科技大学 理学院， 湖南 长沙410073)

摘要：为了构造在光滑区具有较高分辨率并且可以无振荡捕捉激波的高精度有限体积格式，同时降低格式在模板选择上遇到的困难，基于逐维重构方法，发展了结构网格下的高精度有限体积格式，并将这一格式推广到三维曲线坐标系下，从而可以适应相对复杂外形下的计算。为充分验证格式的有效性，选取一系列典型算例进行计算：在等熵涡输运和二维喷管流动中验证了格式的精度可以达到设计精度；在双马赫反射问题中格式也表现出良好的捕捉激波的能力。数值计算表明，上述格式在曲线网格上具有较高的数值精度和鲁棒的激波捕捉能力，适用于流体力学方程的计算。

关键词：有限体积方法；高精度格式；曲线坐标系；逐维重构方法

凭借良好的数值特性和稳定性，有限体积方法被广泛应用于计算流体动力学(Computational Fluid Dynamics,CFD)研究，并被大部分商业软件采用。但是基于此方法的大部分应用和软件都仅限于2阶精度[1]，而随着计算气动声学、大涡模拟、直接数值模拟应用的兴起，高精度格式成为发展趋势。

对于有限体积方法，高精度格式主要依赖于有效无振荡(Essentially Non-Oscillatory，ENO)和加权有效无振荡(Weighted Essentially Non-Oscillatory，WENO)的重构方法。Abgrall[2]，Harten和Chakravarthy[3]，Sonar[4]分别将ENO应用于非结构网格下的有限体积方法。将ENO选择最光滑模板的方法发展为不同模板的非线性加权是WENO格式的基本构造思想。Friedrich[5]最早将WENO应用于非结构网格，但是没有实现最优化，这一工作由Shu等[6]完成。Tsoutsanis等[7]则在三维非结构网格的基础上，研究了任意混合网格的计算方法。最近Groth等[8]发展了一种同样基于光滑度测试的中心有效无振荡(Central Essentially Non-Oscillatory，CENO)格式，并分别用于结构、非结构网格。尽管CENO格式中并没有涉及多模板选择，但仍因其具有ENO特性而命名。

尽管基于ENO/WENO发展了众多的高阶有限体积算法，但是直接在物理空间上执行，特别是在非结构网格上，仍存在较大的问题，尤其是在高阶多维重构中存在模板选择困难，这将严重增加算法和代码的复杂性，并消耗大量的CPU和内存资源，从而无法应用于实际问题的计算。为解决这一问题，一个有效的方法就是在曲线网格下执行有限体积方法。此时需要使用结构网格，尽管灵活性会受到一定的影响，但是可以使用标准的多维重构方法，从而有效降低对计算机内存和CPU的要求。Casper等[9]较早讨论了将高阶ENO格式应用于结构网格的方法，并详细讨论了有限体积下的多维重构。Titarev和Toro[10]给出了三维条件下的多维重构方法，但仅限于笛卡尔网格。

本文以首个应用于临床的KATP开放剂尼可地尔为研究药物，构建高表达瑞典突变型淀粉样前体蛋白的神经母细胞瘤细胞作为AD的体外细胞模型，研究尼可地尔对AD细胞模型氧化应激和Aβ生成的影响，并探讨PI3K/AKT/GSK-3β通路在尼可地尔参与氧化应激、Aβ生成调节中的可能分子机制。

为进一步提高高精度有限体积方法的使用范围，将基于逐维重构的高精度有限体积格式推广到曲线坐标系，使格式在保持较高精度和激波捕捉能力的基础上，适应相对复杂外形下的计算。通过数值算例，验证格式的精度和对流场间断的分辨能力。

1曲线坐标系下的有限体积方法

考虑三维条件下的双曲守恒系统：

将真菌测得ITS rDNA序列以及放线菌16 S rDNA与GenBank数据库中已有的序列进行BLAST比对。结果证明菌株YX-25与Alternaria sp. 的同源性最高为99%。结合已观察到的菌落特征，鉴定为Alternariaalternate。菌株YX-32与Streptomyces sp. 的同源性最高为100%。结合已观察到的菌落特征，鉴定为Streptomycesexfoliatus，见图6、7。

(1)

经过坐标变换(x,y,z)→(ξ,η,ζ)可得：

(2)

网格导数在三维条件下存在多种等价的解析形式，但离散条件下各种表达式的数值表现却有很大差别。使用Deng等[11]在对称守恒网格导数计算方法(Symmetrical Conservative Metric Method, SCMM)中导出的对称守恒形式计算网格导数，如式(9)～(11)所示：

(3)

经过坐标变换，方程中出现网格导数和雅克比。对于静止网格，在曲线网格控制单元Iijk=[ξi-1/2,ξi+1/2]×[ηi-1/2,ηi+1/2]×[ζi-1/2,ζi+1/2]内对控制方程式(2)进行积分，可以得到如式(4)所示关系：

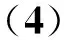
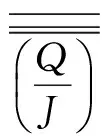
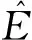
(5)

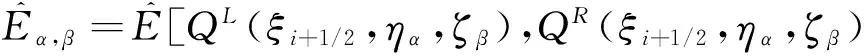
(6)

1.1逐维重构方法

曲线网格的一个重要优势就是可以在计算空间中通过逐维重构计算Gauss点处的QL和QR，而实际应用证明逐维重构是较为简单和节约计算时间的方法，其本质就是在计算Gauss点值时进行多次重构，但每次重构都等价于一维重构。接下来给出这一重构方法的简要说明。

其中：α，β代表η和ζ方向的Gauss点；Kα和Kβ为相应的权系数。那么有限体积方法构造的关键就在于如何得到Gauss点处的QL，QR以及相应的网格导数和雅克比。

(3) 土地开发度：车站周边土地开发强度越高，各种用地性质种类(居住、商业、办公和休闲服务等)越多，线路全日客流的强度就越有保障。本文通过统计车站周边600 m范围内的建筑面积，计算周边用地混合度得到每个车站的折算系数，然后将两者相乘得到车站周边土地开发度指标。

师：我们看出，有些立体图形的表面包含着一些平面图形．反之，我们也可以利用这些平面图形来描述立体图形．请观察手中的四棱锥模型，描述四棱锥的特征．

(7)

由表2可知，反应时间短，铁和硅含量指标明显偏高，随着反应时间的延长，铁和硅含量的急速下降，到2.5h以后，铁和硅含量变化趋于稳定。考虑工作时间效率，最佳反应时间为2.5h。

加强对蔬菜种植户的科技培训，按农时季节和生产需要及时分乡（镇）分村划片开展各类培训，经常深入设施温室大棚集中区进行现场咨询和指导，为广大菜农提供更好的信息和技术服务，提高菜农科学种菜水平和农产品质量安全意识，提高设施蔬菜生产销售的整体水平。建立蔬菜市场价格信息网络，及时提供市场信息，指导蔬菜生产和市场销售。

(8)

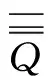
1.2网格导数和雅克比计算方法

2.2二维喷管流动

式中：

然后，利用面元平均值重构得到Gauss点所在沿ζ方向线元上的平均值：

(9)

(10)

(11)

根据积分变换定理可得：

(12)

当假设Q在空间分布为常数时，式(12)可以简化为：

(13)

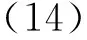
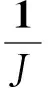
2算例验证

通过对二维、三维算例的计算，验证文中发展的高精度有限体积格式的精度和对激波的捕捉能力。

2.1等熵涡输运

为在曲线网格下验证有限体积格式，本算例中使用波形网格，其可以在均匀网格的基础上通过式(15)得到：

(15)

其中：n=4，A=0.4；L0为计算域的总无量纲长度；j,k,l为网格点坐标索引；x0,y0,z0为对应的坐标值；Δx0，Δy0，Δz0表示均匀网格长度，且满足Δx0=Δy0=Δz0。初始流场为等熵涡：

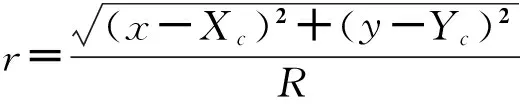
图1中给出了三维网格以及涡输运一个周期后的速度u分布。从图中可以看出，涡结构得到了很好的保持。考虑三维条件下计算量的限制，在二维条件下对这一问题进行了精度测试，表1给出了不同网格下速度v误差的L1范数及计算得到的格式精度。从表中可以看出，在曲线网格下，本文发展的有限体积格式达到了设计的5阶精度，对于光滑流场具有较高的分辨率。

(a)三维网格(a) Three-dimensional grid

(b)速度u等值线(b) Distribution of velocity u图1　三维等熵涡输运网格和计算结果Fig.1　Grid and numerical result in the three-dimensional isentropic vortex transport problem

网格误差精度40×401.020E-0480×809.129E-063.48120×1201.389E-064.64160×1603.416E-074.87240×2404.622E-084.93

（2）热料冷补。热料冷补技术施工时先将坑槽病害处旧路挖除并清理洁净，然后添加新沥青混合料并整平压实。该技术施工成本较低，适合大面积开展且修补效率较高，但存在弱接缝，受天气影响大，无法对病害进行及时快速修补。

为了进一步验证格式在管道流动中的模拟能力，选取Euler方程控制的等熵二维喷管流动进行计算。Casper等[13]最早对这一问题进行了研究。在本文中使用C3外形，中间段的形状通过式(17)拟合：

(17)

此算例中包含亚声速入口、出口及滑移边界条件。图2为喷管外形和网格示意图。

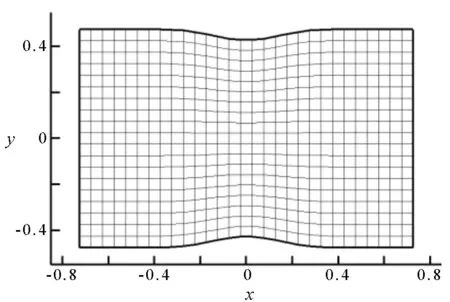
图2　二维喷管外形和网格Fig.2　Configuration and mesh used in the two-dimensional channel flow

图3给出了计算得到的流场压力，从图中可以看出压力分布对称。表2中给出了流场熵误差的L1范数和计算得到的格式精度。从表中可以看出，由于在边界处格式的精度要适当降低，总体精度略小于5.0，但格式仍可以保持较高的数值精度，这表明本文使用的格式在管道流动中也有较好的效果。

该微信小程序由俄语研习社研发设计，提供原创文章、刷题、翻译学习三方面内容。其中刷题方面针对俄语专业考级（四级和八级），提供1998年-2018年的俄语专业四级全部选择真题及2003-2018年的俄语专业八级全部选择真题。俄语四级选择真题共分为30课时，每人每天可解锁2课时；俄语八级选择真题共分为30课时，每人每天可解锁10课时。该程序还设有课程列表，可查看已选课程的完成情况。不仅如此，在每个课时的下方，用户可见其他用户做完该课时所花费的时间、准确率及分数。该程序设有积分规则，可以累积分数。根据积分总数，使用者可随时查看自己在参加该课程的微信用户中的排名，这项功能能够为用户的学习提供动力。

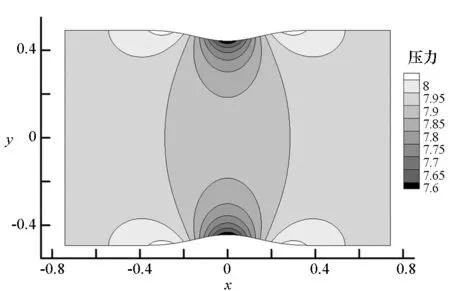
图3　二维喷管流动压力分布Fig.3　Distribution of the pressure in the two-dimensional channel flow

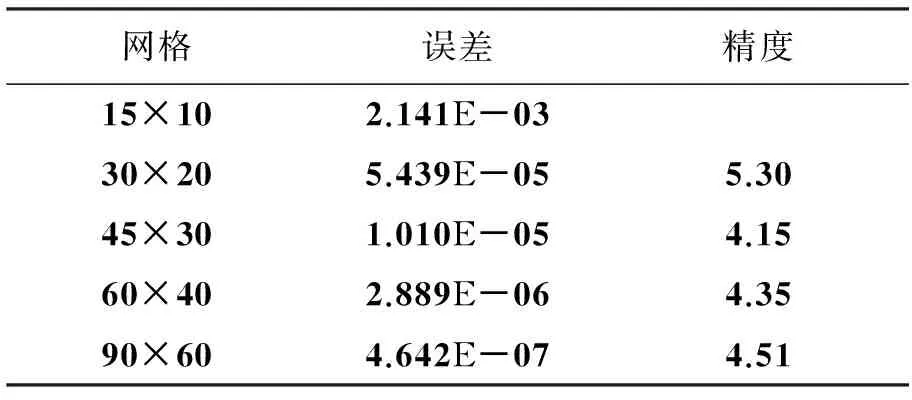
网格误差精度15×102.141E-0330×205.439E-055.3045×301.010E-054.1560×402.889E-064.3590×604.642E-074.51

2.3双马赫反射

为了考核高精度有限体积格式在激波捕捉方面的能力，对双马赫反射问题进行了计算。算例的计算域为[0,4]×[0,1]，反射位置从下壁面1/6处开始，初始时刻马赫数为10的右行激波位于(1/6,0)，并与壁面成60°角。上边界条件设为精确的激波移动条件，整个数值计算进行到t=0.2。

一般双马赫反射问题都在笛卡尔网格下计算，但为了测试本文中高精度有限体积格式在曲线网格下的应用，同时在随机网格上进行了计算。随机网格的生成方法是在笛卡尔网格的基础上对网格坐标增加一个随机量。这一过程由Fortran程序控制，但不会超过当地步长的20%。文中使用240×60的计算网格。图4中分别给出了笛卡尔网格和随机网格下的计算结果。从图中可以看出，两种网格下的计算结果基本相同，并且格式都很好地捕捉到了激波结构。这表明本文中使用的高精度有限体积格式同样具有很好的激波捕捉能力。

展开部长达120个小节（第95至214小节），在g小调上开始，使用了主部的主题材料。经过一系列的离调（a小调、d小调、c小调、降b小调）之后，在第150小节上，以降b小调出现了“假再现部”。然后在第161小节持续强调低音的降B音，右手则以半音上升，达到升G音，形成增六和弦，以不断增强的力度，强力返回到d小调的属和弦，为再现部的出现作准备。尾声之前再次出现类似手法，第323小节起，贝多芬不断地重复一个短小的音型，先是g小调，然后a小调，在第335小节，低音A持续了整整十六个小节，渐弱至pp，突然以ff返回主题，进入尾声，其效果极其富有戏剧性。

“这种事连我都不信，你们还当真了。”一向自诩为爱和正义化身的夏霖听到这个传闻后就开始怀疑真实性。在同学们眼中，夏霖一直是个中二少女，但看过上百本奇幻小说的她却觉得自己是个魔法少女，天不怕地不怕。于是，她决定去现场一探究竟。

(a)笛卡尔网格下计算结果(a) Result on Cartesian grid

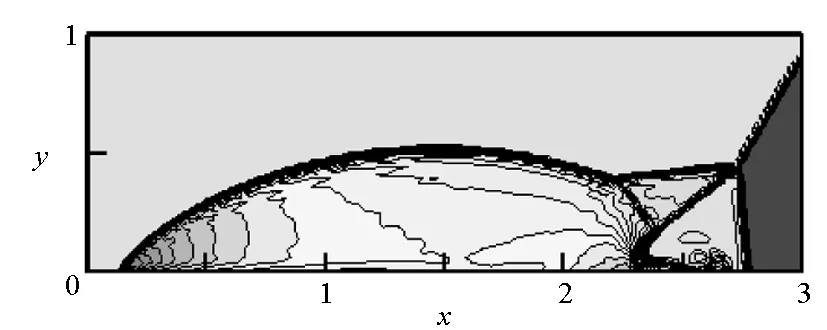
(b)随机网格下计算结果(b) Result on randomized grid图4　双马赫反射计算结果Fig.4　Results in the double Mach reflection problem

3结论

将基于逐维重构方法的高精度有限体积方法推广到三维曲线坐标系，讨论了曲线坐标系下的重构方法和网格导数、雅克比的计算方法。通过涡输运算例和喷管流动算例的计算，证明格式可以实现设计的精度，具有较高的空间分辨率。在双马赫反射算例中，一方面验证了格式具有良好的激波捕捉能力，另一方面也表明格式具有较强的网格适应能力，在随机网格上也可以得到较好的数值结果。在接下来的工作中，将考虑实现黏性项处理的高精度，从而将格式推广到NS方程的计算。

参考文献(References)

[1]Calhoun D A, Helzel C, LeVeque R J. Logically rectangular grids and finite volume methods for PDEs in circular and spherical domains [J]. SIAM Review, 2008, 50(4): 723-752.

[2]Abgrall R. On essentially non-oscillatory schemes on unstructured meshes analysis and implementation [J]. Journal of Computational Physics, 1994, 114(1): 45-58.

[3]Harten A, Chakravarthy S R. Multi-dimensional ENO schemes for general geometries [R]. ICASE Report No. 91-76, 1991.

[4]Sonar T. On the construction of essentially non-oscillatory finite volume approximations to hyperbolic conservation laws on general triangulations: polynomial recovery, accuracy and stencil selection [J]. Computer Methods in Applied Mechanics and Engineering, 1997, 140(1/2): 157-181.

[5]Friedrich O. Weighted essentially non-oscillatory schemes for the interpolation of mean values on unstructured grids [J]. Journal of Computational Physics, 1998, 144(1): 194-212.[6]Hu C Q, Shu C W. Weighted essentially non-oscillatory schemes on triangular meshes [J]. Journal of Computational Physics, 1999, 150(1): 97-127.

[7]Tsoutsanis P, Titarev V A, Drikakis D. WENO schemes on arbitrary mixed-element unstructured meshes in three space dimensions [J]. Journal of Computational Physics, 2011, 230(4): 1585-1601.

[8]McDonald S D, Charest M R J, Groth C P T. High-order CENO finite-volume schemes for multi-block unstructured mesh [C]//Proceedings of 20th AIAA Computational Fluid Dynamics Conference, AIAA 2011-3854, 2011.

[9]Casper J, Atkins H L. A finite-volume high-order ENO scheme for two-dimensional hyperbolic system [J]. Journal of Computational Physics, 1993, 106(1): 62-76.

[10]Titarev V A, Toro E F. Finite-volume WENO schemes for three-dimensional conservation laws [J]. Journal of Computational Physics, 2004, 201(1): 238-260.

[11]Deng X G, Min Y B, Mao M L, et al. Further study on geometric conservation law and application to high-order finite difference schemes with stationary grids [J]. Journal of Computational Physics, 2013, 239: 90-111.

[12]Abe Y, Haga T, Nonomura T,et al. On the freestream preservation of high-order conservative flux-reconstruction schemes [J]. Journal of Computational Physics, 2015, 281: 28-54.

[13]Casper J, Shu C W, Atkins H. A comparison of two formulations for high-order accurate essentially non-oscillatory schemes[J]. AIAA Journal, 1994, 32(10): 1970-1977.

doi:10.11887/j.cn.201602010

*收稿日期：2015-09-19

基金项目：国防科学技术大学科研计划资助项目(ZDYYJCYJ20140101)

作者简介：徐丹(1987—)，男，山东威海人，博士研究生，E-mail：13786146863@163.com；邓小刚(通信作者)，男，教授，博士，博士生导师，E-mail：xgdeng2000@vip.sina.com

中图分类号：V211.3

文献标志码：A

文章编号：1001-2486(2016)02-056-05

High-order finite volume schemes in three-dimensional curvilinear coordinate system

XU Dan1, WANG Dongfang1, CHEN Yaming2, DENG Xiaogang1

(1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China;2. College of Science, National University of Defense Technology, Changsha 410073, China)

Abstract：In order to develop a high-order finite volume scheme, which can perform with high fidelity in smooth regions, capture the discontinuities without oscillation, and overcome the difficulty in choosing stencils, a high-order finite volume scheme on structure meshes was developed on the basis of dimension-by-dimension reconstruction method. The scheme was also extended to the three-dimensional curvilinear coordinate system, which was suitable for the computation under relatively complex configurations. In order to validate the numerical scheme, some test cases were used. In the cases of the isentropic vortex and two-dimensional channel flow, it was found that the designed order of accuracy could be achieved. In the double Mach problem, it was proved that the scheme could well capture the discontinuities. The test cases show that the scheme has high numerical accuracy and robust capturing ability on curvilinear meshes and high efficiency in the simulations of the computational fluids dynamics.

Key words：finite volume method; high-order scheme; curvilinear coordinate system; dimension-by-dimension reconstruction method

http://journal.nudt.edu.cn