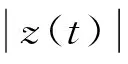引入电流变化率的电源分布网络最差噪声分析算法*

赵振宇，孙　浩，邓　全，蒋剑锋

(国防科技大学 计算机学院， 湖南 长沙　410073)



引入电流变化率的电源分布网络最差噪声分析算法*

赵振宇，孙浩，邓全，蒋剑锋

(国防科技大学 计算机学院， 湖南 长沙410073)

摘要：随着时钟频率的增加以及电源电压的降低，电源完整性问题日益凸显。将电流变化率加入到最差噪声算法的电流约束中，能够在任意电流变化率的情况下分析电源分布网络的最差噪声，从而获得更加真实的最差噪声。另外，利用改进的Knuth-Yao四边形不等式法对基于动态规划的最差噪声算法进行加速，加速后算法的时间复杂度从O(n2m)降为O(mnlogn)。

关键词：动态规划；最差噪声；变化率；电源分布网络；时域分析

最差噪声估计的目标是在不清楚芯片准确负载电流的情况下，为封装以及印刷电路板(Printed Circuit Board, PCB)设计者提供验证电源分布网络的可靠方法[1-2]。这是因为，在芯片设计完成之前，很难得到芯片上负载电流的详细信息。即使在芯片设计完成之后，也很难确定所有的输入情况能获得所有可能的输出电流。此外，为了保证系统的鲁棒性，模拟时必须遍历所有的输入电流，这样的代价是昂贵的。

为了描述不确定负载电流，Kouroussis和Najm[3]提出了“电流约束”这个概念。这个概念是合理的，因为，在芯片设计完成之前，芯片设计者即使不能够完整地掌握负载电流的信息，但还是对负载电流有一定程度的了解。这些了解可能基于前面的设计者，也可能基于设计初期的系统级模拟[4-5]。封装以及PCB设计者就可以利用这些信息对电源分布网络进行初期的验证[6]。然而，之前的一些工作仅考虑了电流幅值这个约束，却没有考虑电流的变化率，这会导致所估计的最差噪声过分悲观。因此，本文所构建的电流约束将考虑电流的最小变化率。

1问题定式化

最差噪声算法的目的是在电流约束下确定芯片的最差噪声[7-8]。如上一小节所述，负载电流的一个约束条件就是电流幅值，约束条件可以通过下面的式(1)表示：

0≤i(t)≤b, ∀t≥0

(1)

其中，b代表瞬态电流i(t)的上边界。在此约束条件下，电流变化率tr代表电流从0变化到b所需要的时间或者从b变化到0所需要的时间。此外，再增加一个电流约束条件，变化率的下边界tb，即tr≥tb。最小变化率的约束条件可以通过最大电流斜率的形式来表示：

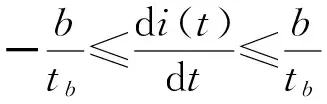
其中b/tb为电流的最大斜率。

将电源传输系统噪声表示为v(t)。为了简化分析过程，假设电压源Vdd为零。这样，噪声v(t)可以表示为输入电流和系统单位脉冲响应的卷积为：

(2)

其中z(τ)代表系统单位脉冲响应。由于卷积过程会对v(t)产生累加效果，我们将积分时间t设置为脉冲响应衰减到可以忽略的时候。通过将式(2)中i(t-τ)替换为一般函数f(τ)，将积分变量由τ变换为t，可以将最差噪声定式化为：

s.t.0≤f(t)≤b,∀t≥0

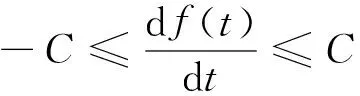
(3)

其中C=b/tb表示f(t)斜率的上边界。一旦确定了f(t)，相应的最差负载电流可以通过i(t)=f(T-t)得到。

值得注意的是，式(3)通过电流方向计算得到的是最大压降。电源传输系统的电感效应会引起Ldi/dt噪声，包括压降和偏差。对于最大偏差，仅需要在同样约束条件下，将式(3)中原函数进行最小化。因此，本文后面的内容主要是针对最大压降进行分析。

2最差噪声分析算法

首先，将卷积时间[0,T]分为m个时间段[t0=0,t1], [t1,t2],…,[tm-1,tm=T]，以保证系统单位脉冲响应在每一个时间段不发生正负变化，如图1所示。同时，在电流约束范围[0,b]选择n+1个采样点u0=0,u1,…,un-1,un=b，n的取值由计算精度要求决定。

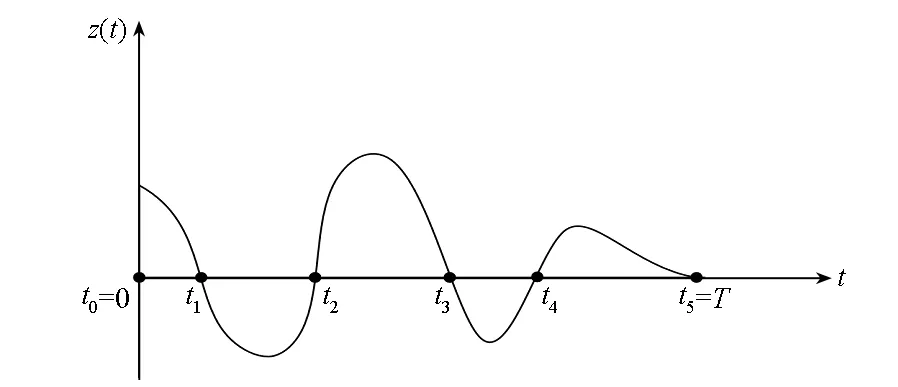
图1　卷积时间分段方法Fig.1　Division of convoluting time

选择一个时间段[tj,tj+1]，将Gj(k,i,t)定义为从tj时刻的uk到tj+1时刻的ui所产生的最差f(t)。将Vj(k,i)定义为对应的最差噪声。我们就可以得到：

(4)

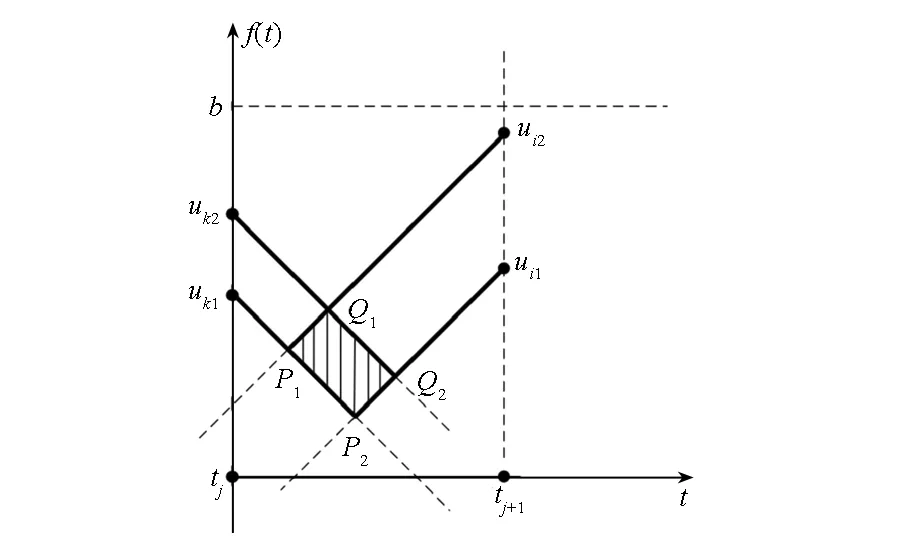
利用贪婪算法很容易地计算Gj(k,i，t)。如图2(a)和图2(b)所示，如果z(t)在[tj,tj+1]时间段为正，则从uk画一条斜率为C的直线，另外画一条到ui结束的直线，斜率为-C。如果两条直线在低于电流上边界b的地方相交，则Gj(k,i,t)为uk→P→ui，如图2(b)所示。如果直线交点高于上边界b，则将边界与两条直线的交点分别用P1和P2表示，Gj(k,i,t)为uk→P1→P2→ui，如图2(a)所示。

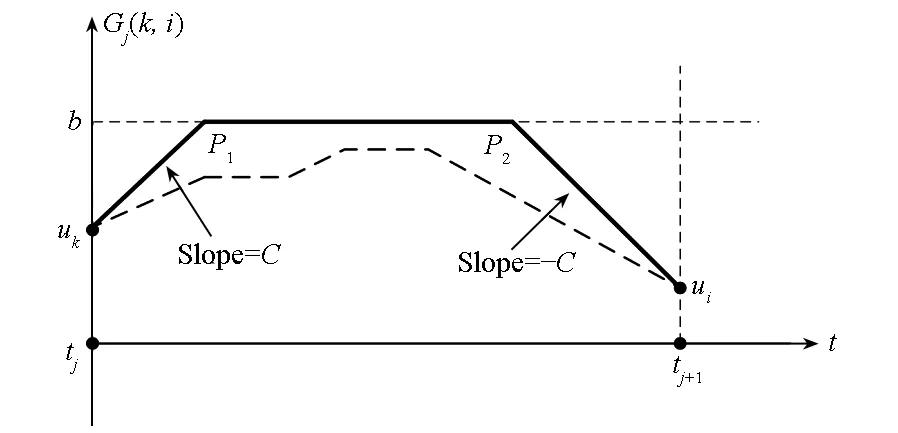
(a)交点超过边界(a) Intersection over border

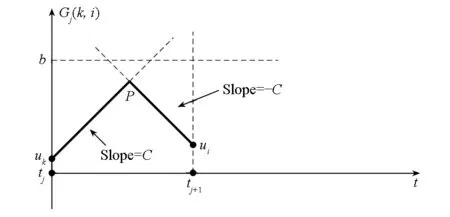
(b)交点未超过边界(b) Intersection under border图2　贪婪算法Fig.2　Greedy algorithm

如果z(t)在[tj,tj+1]时间段为负，Gj(k,i,t)可以表示为类似形式。以图2(a)所示情况为例来证明贪婪算法。假设G′j(k,i,t)为未经贪婪算法处理的f(t)，如图2(a)中虚线所示，可得在[tj,tj+1]上G′j(k,i,t)≤Gj(k,i,t)。由于z(t)在[tj,tj+1]为正，可得：

(5)

这就表示Gj(k,i)是在上述约束下的最差f(t)。

考虑Cr+1(r≥2)映射F:Ω⊆Cn→Cn，其中Ω是Cn中的一个原点领域.假设F(0)=0是F(x)在原点领域的不动点，因此可将F(x)表示为：

将OPT(j,i)(j∈[0,m],i∈[0,n])定义为电流停留在tj时刻电流值为ui时的最差噪声。OPT的一些基本特性如下：

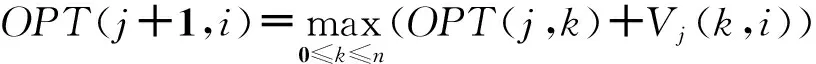
3算法加速

如果利用迭代方法计算OPT的所有值，时间复杂度为O(n2m)[9-10]。本小节，将通过一些方法对动态规划算法进行提速，经过算法加速，时间复杂度降低为O(mnlogn)。

3.1优化问题的性质分析

假设z(t)在[tj,tj+1]时间段为负，将Wj(k,i)定义为Gj(k,i,t)的绝对值，而Fj(k,i)为对应于k的OPT(j+1,i)候选值，即Fj(k,i)=OPT(j,k)-Wj(k,i)。关于W和F有以下几条有用的性质：

引理1：对任何0≤k1

Wj(k2,i2)-Wj(k1,i2)≤Wj(k2,i1)-Wj(k1,i1)

图3　函数W的四边形不等式Fig.3　Quadrangle inequality for the function W

值得注意的是，引理1就是W的四边形不等式[11]。然而，该不等式并不成立，也就是说无法推导出OPT的四边形不等式。因此，选择基于下面一条引理的Knuth-Yao加速方法来降低算法的时间复杂度。

引理2：假设k1i1，可以得到Fj(k1,i2)≤Fj(k2,i2)。

证明：

根据引理2，假设k1

i0=GetTransPos(j,k1,k2)

3.2加速算法伪代码描述

将S定义为OPT(j+1,i)的候选值k从小到大排列的队列。将Q定义为数据越小优先级越高的优先队列，队列可进行GetMin，DeleteMin和Add三种操作。GetMin和DeleteMin分别能够获取和删除优先队列中的最小元素，而Add(e)操作则可以将元素e插入到队列中。上述三种操作均可在时间复杂度O(logn)内完成。队列中每一个元素都包括三个分量：第一个分量是优先队列的关键码(key)，它表明了i0的位置。后面两个分量k1和k2对应于i0。加速动态规划算法可以通过伪代码“算法1”表示，该算法的时间复杂度为O(nlogn)。

算法1　加速优化

3.3时间复杂度

S队列可以通过双向链接表实现，同时还需要一个指针给出每一个k在S中的位置。这样，算法中第8步和第9步可在瞬间完成。更进一步，算法1中每一个候选值k仅能被删除n次，因此，第6步到第12步整个过程中最多运行n次。GetMin，DeleteMin和Add三种操作的时间复杂度为O(logn)，GetTransPos()的时间复杂度也为O(logn)。因此算法1的时间复杂度为O(nlogn)。

对于OPT，仅需对每一个i初始化OPT(0,i)=0，调用GetOPT算法m次，因此，OPT的时间复杂度为O(mnlogn)。

3.4算法加速效果

分别利用加速前算法和加速算法进行最差噪声估计，并对两种算法的运行时间进行对比，以检验算法的加速效果。算法通过C++语言实现，并运行于配置为2 GB内存，CORE i5的计算机。单位脉冲响应分为12段，即m=12。加速前算法与加速算法运行时间与电流采样点个数n的关系如图4所示。由图可知，加速算法的运行时间要远远小于加速前算法的运行时间，尤其当n足够大的时候。

图4　算法加速前后运行时间对比Fig.4　Run time comparison between the of O(n2m) algorithm and the O(mnlogn) algorithm

4结论

对最差噪声算法进行优化，引入电流变化率，反映了更真实的最差噪声，避免只考虑电流幅度所估计的较为悲观的最差噪声。同时利用Kunth Yao四边形不等式法对动态规划算法进行加速，有效地降低了运算的复杂度，从O(n2m)降为O(mnlogn)。在大规模集成电路设计中仿真时间收益明显，为后续电源的网络问题打下基础。

参考文献(References)

[1]Hu X, Zhao W B, Du P, et al. On the bound of time-domain power supply noise based on frequency-domain target impedance[C]//Proceedings of the 11th International Workshop on System Level Interconnect Prediction, ACM, 2009: 69-76.

[2]Wang Y Z, Hu X, Cheng C K, et al. A realistic early-stage power grid verification algorithm based on hierarchical constraints[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2012, 31(1): 109-120.

[3]Kouroussis D, Najm F N. A static pattern-independent technique for power grid voltage integrity verification[C]//Proceedings of the 40th Annual Design Automation Conference, ACM, 2003: 99-104.

[4]Abdul Ghani N H, Najm F N. Fast vectorless power grid verification using an approximate inverse technique[C]//Proceedings of the 46th Annual Design Automation Conference, ACM, 2009: 184-189.

[5]Ferzli I A, Najm F N, Kruse L. A geometric approach for early power grid verification using current constraints[C]//Proceedings of the IEEE/ACM International Conference on Computer-aided design, 2007: 40-47.

[6]Xiong X, Wang J. Verifying RLC power grids with transient current constraints[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2013, 32(7): 1059-1071.

[7]Zhu H, Wang Y, Liu F, et al. Efficient transient analysis of power delivery network with clock/power gating by sparse approximation[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2015, 34(3): 409-421.

[8]Ferzli I A, Chiprout E, Najm F N. Verification and codesign of the package and die power delivery system using wavelets[J]. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2010, 29(1): 92-102.

[9]Zhao W, Cai Y, Yang J L. A multilevel 64-matrix-based approximate matrix inversion algorithm for vectorless power grid verification[C]//Proceedings of the 18th Asia and South Pacific Design Automation Conference (ASP-DAC), IEEE, 2013: 163-168.

[10]Zhao W, Cai Y, Yang J L. Fast vectorless power grid verification using maximum voltage drop location estimation[C]//Proceedings of the 19th Asia and South Pacific Design Automation Conference (ASP-DAC), IEEE, 2014: 861-866.[11]Yao F F. Efficient dynamic programming using quadrangle inequalities[C]//Proceedings of the 12th Annual ACM Symposium on Theory of Computing, ACM, 1980: 429-435.

doi:10.11887/j.cn.201602014

*收稿日期：2015-03-09

基金项目：国家自然科学基金资助项目(61272139)

作者简介：赵振宇(1973—)，男，辽宁朝阳人，研究员，博士，E-mail：zyzhao@nudt.edu.cn

中图分类号：TN47

文献标志码：A

文章编号：1001-2486(2016)02-082-05

A time-domain worst-case noise algorithm for power delivery network with non-zero current transition times

ZHAO Zhenyu, SUN Hao, DENG Quan, JIANG Jianfeng

(College of Computer, National University of Defense Technology, Changsha 410073, China)

Abstract：With the increasing of clock frequency and the decreasing of supply voltage, power integrity becomes a critical issue. The effect of the transition time of load currents was taken into account, and a more realistic worst-case noise prediction was obtained. In addition, a dynamic programming algorithm is introduced for the time-domain impulse response of the power distribution system, and a modified Knuth-Yao quadrangle inequality speedup method is developed which reduces the time complexity of the algorithm from O(n2m) to O(mnlogn).

Key words：dynamic programming; worst-case noise; transition time; power delivery network; time-domain analysis

http://journal.nudt.edu.cn