球形永磁阵列振动能量收集器设计与优化

丁志强， 陈仁文， 章飘艳， 夏桦康， 杨　沛

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京　210016)



球形永磁阵列振动能量收集器设计与优化

丁志强， 陈仁文， 章飘艳， 夏桦康， 杨沛

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京210016)

摘要：为实现多方向环境能量收集，设计球形电磁式振动能量采集器。基于二维Halbach阵列设计的球面Halbach永磁阵列，较传统永磁阵列能提高线圈中磁链变化梯度，从而提高结构输出性能；建立数学解析模型，据解析结果对模型各参数进行优化；对该模型进行有限元仿真分析及实验性能测试。结果表明，该模型能有效响应空间任意方向振动，进而转化为电能；外部激励为10 Hz、激励为水平方向、负载阻值50 Ω时，该球形振动能量采集器输出电能达最大，单个线圈中最大负载功率可达0.8 mW。

关键词：振动能量采集；电磁式；多方向；Halbach阵列；有限元

随科学的高速发展，环境能量采集技术应运而生[1]。环境能量采集指将自然界中广泛存在的环境能量如太阳能、风能、热能、振动能等利用各种换能材料或结构转换成电能并存储利用[2]。而环境能量中的振动能作为最常见能量形式可通过能量收集装置收集，用于补充或取代传统的电力供应。环境振动能量具有高效、便携、环保、性价比高等优点，因而具有较高研究价值及应用前景[3]。目前环境振动能量采集主要有静电式[4-5]、电磁式[6-10]及压电式[11-13]三种，其中电磁式振动能量采集器以体积小、输出电能大等最具优势。本文采用电磁式。

电磁式振动能量采集结构主要含拾振系统及换能系统。前者一般由弹簧、悬臂梁、质量块等组成，后者由线圈、磁体、铁轭等组成。以往研究中，振动能量采集装置只能收集单个或几个特定方向的振动能量，与环境振动的随意性、多方向不符，为此，本文设计出球形能量采集结构，能有效收集环境中各方向振动能，大大提高其适用性[14]。而针对换能结构多为单一永磁体，导致磁路设计单一及线圈磁链变化梯度较小，本文结合Halbach永磁阵列[15-17]设计出足球型换能系统，建立数学模型，据解析式进行结构参数优化，并与仿真结果对比，验证本文球形结构的可行性。

1球形振动能量收集器结构

新型球形振动能量收集装置示意图见图1。中间球形永磁阵列为质心偏离形心转子，线圈、存储电路镶嵌于内球壳，内、外球壳相互固定作为定子。球形永磁阵列用Halbach阵列以减弱球体内部磁场、加强球体外部磁场。当外界给整个球形振动能量收集器任意方向冲击或转矩时，内部偏心球形磁铁阵列会在重力作用下与外部定子线圈发生相对转动，使线圈切割磁力线产生电能，通过存储电路收集利用。

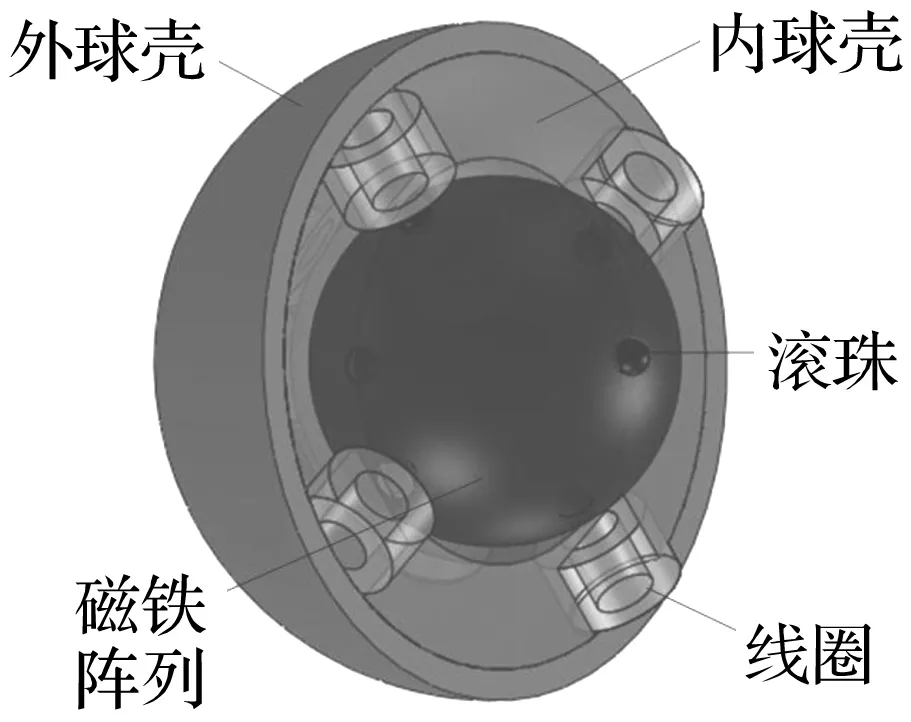
图1　球形振动能量收集装置示意Fig.1 Spherical vibration energy harvester

2Halbach阵列

Halbach永磁体阵列为新型方式，可有效增加单边磁场，达到用少量永磁体能满足磁场强度要求效果。该阵列将磁化方向按一定规律排布，主要包括直线形、圆形、环形等。图2为普通径向永磁阵列与典型直线形Halbach阵列励磁效果图。由图2看出，较径向永磁阵列，直线型Halbach永磁阵列减弱下部空间磁场、有效增强上部空间磁场，忽略端部效应后，可将直线型Halbach阵列视为单边磁场，使Halbach阵列在某些场合亦能应用。

图2　不同永磁阵列励磁效果图Fig.2 Excitation effect of different magnet arrays

3球形阵列永磁体模型

3.1足球形永磁阵列模型

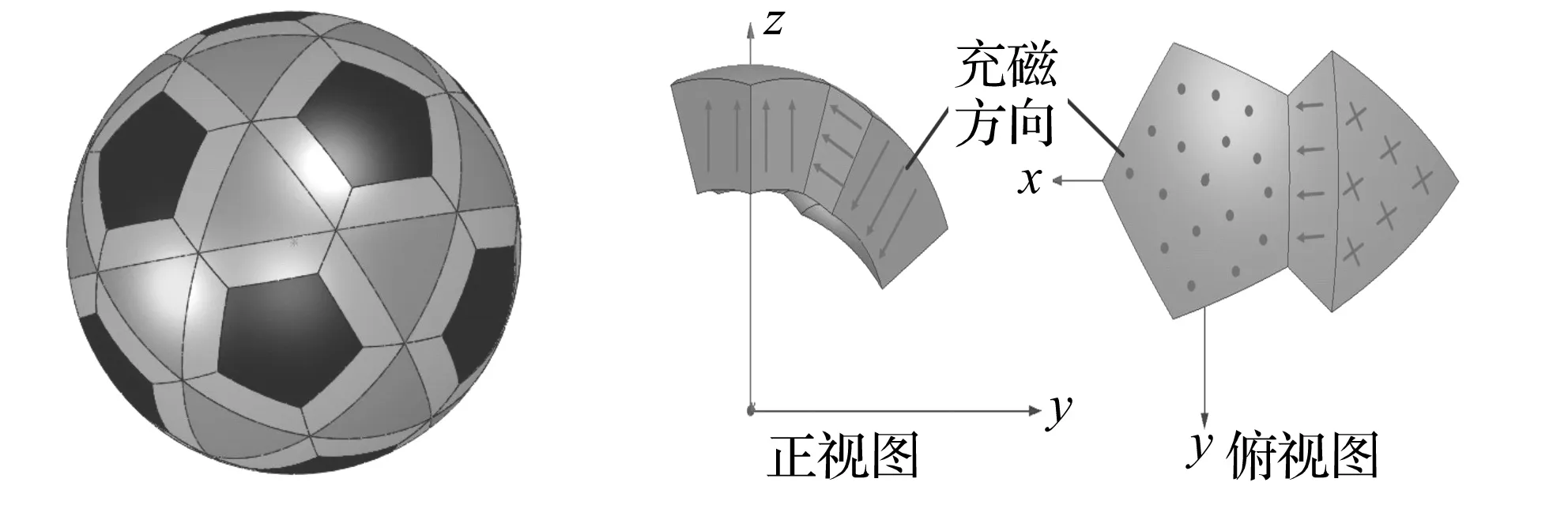
球形振动能量收集器中磁铁阵列采用类似Halbach阵列方式，具体排布见图3，可见形状像足球。传统足球含12个五边形块及20个六边形块。永磁阵列中，将每个六边形块分解成1个中心三角形块及3个梯形块。12个五边形磁铁充磁方向由球心指向五边形面心，20个三角形磁铁充磁方向由三角形面心指向球心，其余60个梯形磁铁充磁方向由与梯形相邻的三角形面心指向与五边形面心。其中3块相邻五边形、三角形、梯形磁铁、外部气隙及线圈组成一磁阻回路，充磁方向见图4。

3.2足球形永磁阵列的等效磁路模型

3.2.1球形永磁阵列模型建立

球形永磁铁阵列磁场在空间各方向呈对称分布，分析永磁阵列等效此路模型时可取其中相邻3块磁铁组成磁铁回路，见图5，其中S1，S2，S4分别为3块磁铁上表面灰色区域面积；S3为梯形磁铁截面积。

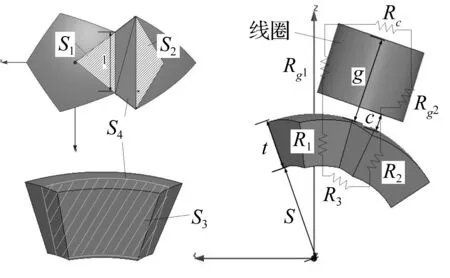
图5　球形永磁阵列中相邻3块磁铁尺寸Fig.5 The dimensions of 3 adjacent magnets in the football-shape magnet array

足球形永磁阵列中每个梯形磁铁均与1个五边形磁铁及1个三角形磁铁相邻，与气隙、线圈共同组成磁阻回路。设此磁阻回路无磁漏并忽略外球壳磁阻RC，由磁路基本原理得

(R1+R2+R3+RG)Φg=HCds

(1)

式中：R1，R2，R3为五边形磁铁S1部分磁阻、三角形磁铁S2部分磁阻及梯形S4磁阻；RG为两气隙磁阻之和；Φg为气隙磁通量；ds为相邻3块磁铁沿充磁方向总厚度；同时设k=t+s为球形永磁阵列半径；c为线圈与永磁阵列气隙间距；d，D为线圈内外径；HC，Br，μr为永磁体矫顽力、剩磁强度及回复磁导率,μ0为真空磁导率。

3.2.2足球模型几何参数计算

设足球半径为r，表面积为S。将足球表面曲面的五、六边形视为平面，边长均为l，得

(2)

求解式(2)得足球几何参数为

(3)

3.2.3气隙磁通参数解析

气隙横截面积S5可表示为

S5=S1′+S2′+S4′

(4)

式中：S1′，S2′，S4′为半径k+g/2球面部分对应半径k的球面S1，S2，S4部分，结合式(2)计算得

S5=0.209 42(s+t+g/2)2

(5)

计算3块磁铁总厚度ds为

ds=0.18s+2.09t

(6)

永磁体、气隙磁阻分别表示为

(7)

将以上数值代入式(1)，得气隙磁通Φg为

(8)

取HC=1.353×106A/m，μr=0.823，μ0=4π×10-7T·m/A，得

(9)

气隙磁通密度Bg及永磁体磁通密度Ba关系(忽略磁漏)为

BgAg=BaAa

(10)

永磁体总厚度ds用气隙磁通密度Bg表示为

(11)

气隙磁通密度Bg表示为

(12)

3.2.4线圈阻尼解析

当球形永磁阵列振动能量收集器不接负载，即将线圈短接时可计算单个线圈绕组产生的阻尼为

P=cv2

(13)

式中：P为线圈磁路总功率；c为线圈绕组产生的阻尼；v为线圈垂直磁场方向速度分量。

据法拉第电磁感应定律得线圈在磁场中切割磁力线产生的电动势为

U=Bvl

(14)

式中：B为线圈的磁场磁感应强度；L为切割磁场线圈长度；ρ为线圈导线电阻率。

本文结构中设线圈匝数为N，线圈整体横截面积为AC；平均直径为DC，线圈中单根导线横截面积为AW；直径为dw，计算得

(15)

据以上公式可推导出单个线圈绕组阻尼为

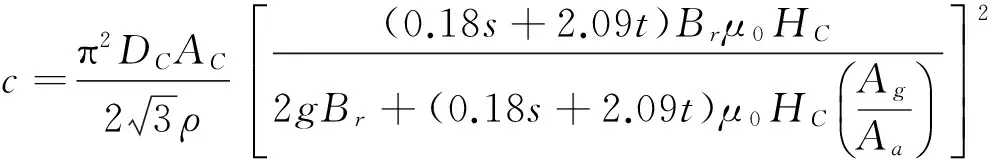
4球形永磁阵列模型参数优化

据式(16)分析永磁阵列中不同尺寸参数对气隙磁通影响，进行优化设计。

球形永磁阵列总半径为k=t+s，令α=t/k，气隙磁通Φg与参数α、g、k关系见图6。由图6看出，球形永磁阵列半径k不变时气隙磁通Φg随α增大先急剧增大再缓慢变小，α≈0.2时达到峰值，气隙间距g越大Φg越小；g不变时Φg随球形半径增大而增大，因α不变k越大其中各永磁尺寸越大，气隙磁通会越大。

考虑整个结构尺寸，取α=0.2。令β=t/(t+s+g)、DS=t+s+g、Da=t+s+c，代入式(16)，结合表1的参数组合，得单个线圈阻尼c与参数β关系，见图7。由图7看出，单个线圈阻尼c随其外径与内径平方差(即D2-d2)的增加显著增加。在整个半径DS及线圈参数确定时c随β增大先增大再减小，β≈0.15时达峰值，β≈0.18时降到0。线圈参数确定时c随DS的增加显著增加。由于设计尺寸限制，取DS=40。表2为优化设计后结构中各参数最终尺寸。

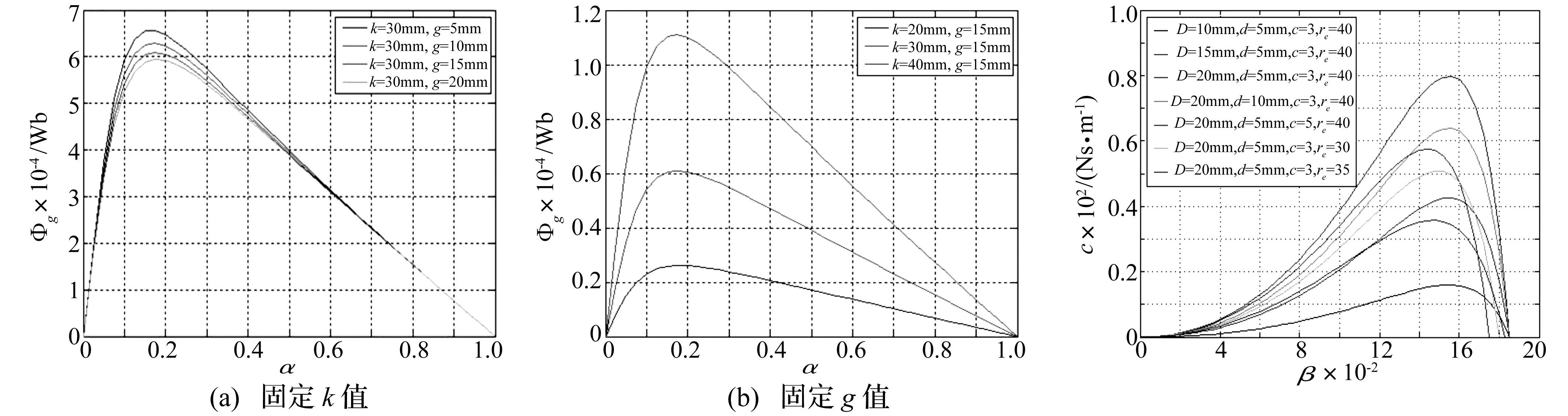
图6 气隙磁通Φg与参数α,g,k关系Fig.6RelationshipbetweenΦgandα,gandk图7 单个线圈阻尼c与参数β关系Fig.7Therelationshipbetweencandβ

表1　结构尺寸参数组合

表2　结构优化后各参数尺寸(单位：mm)

5结果分析及仿真比较

设动子永磁阵列在外激励作用下与定子线圈发生角速度为ω的相对运动，气隙磁通在球形永磁阵列外表面按永磁体分布成正弦变化，即

(17)

得单个线圈绕组感应电动势为

E=-2.492×10-4ωNcos(4ωt)

(18)

设动子永磁阵列相对定子线圈运动角速度为ω=4πrad/s，单个线圈匝数为N=50，代入式(18)，得本文的球形永磁阵列振动能量收集器在一定环境振动条件下产生的能量为

E=-0.181 6cos(4.815wt)

(19)

为验证上述理论的正确性，用Ansoft Maxwell 2D分析球形永磁阵列在稳态时的磁密度云；再用Ansoft Maxwell 3D对结构进行瞬态仿真。图8、图9为通过Ansoft Maxwell 3D静磁场仿真所得结果。由两图看出，球形永磁体表面产生类似于正弦的磁链变化梯度，使动子永磁体相对定子线圈发生转动时，线圈中磁链能发生剧烈变化，从而产生较强的感应电动势。

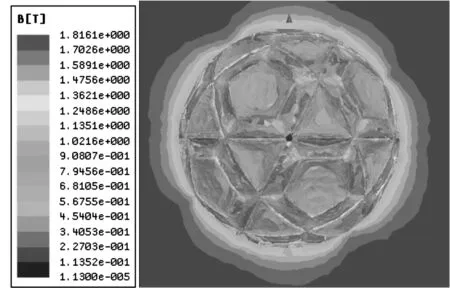
图8　球形永磁阵列稳态时磁密度云图Fig.8 Magnetic density contours of the spherical magnet array at steady state

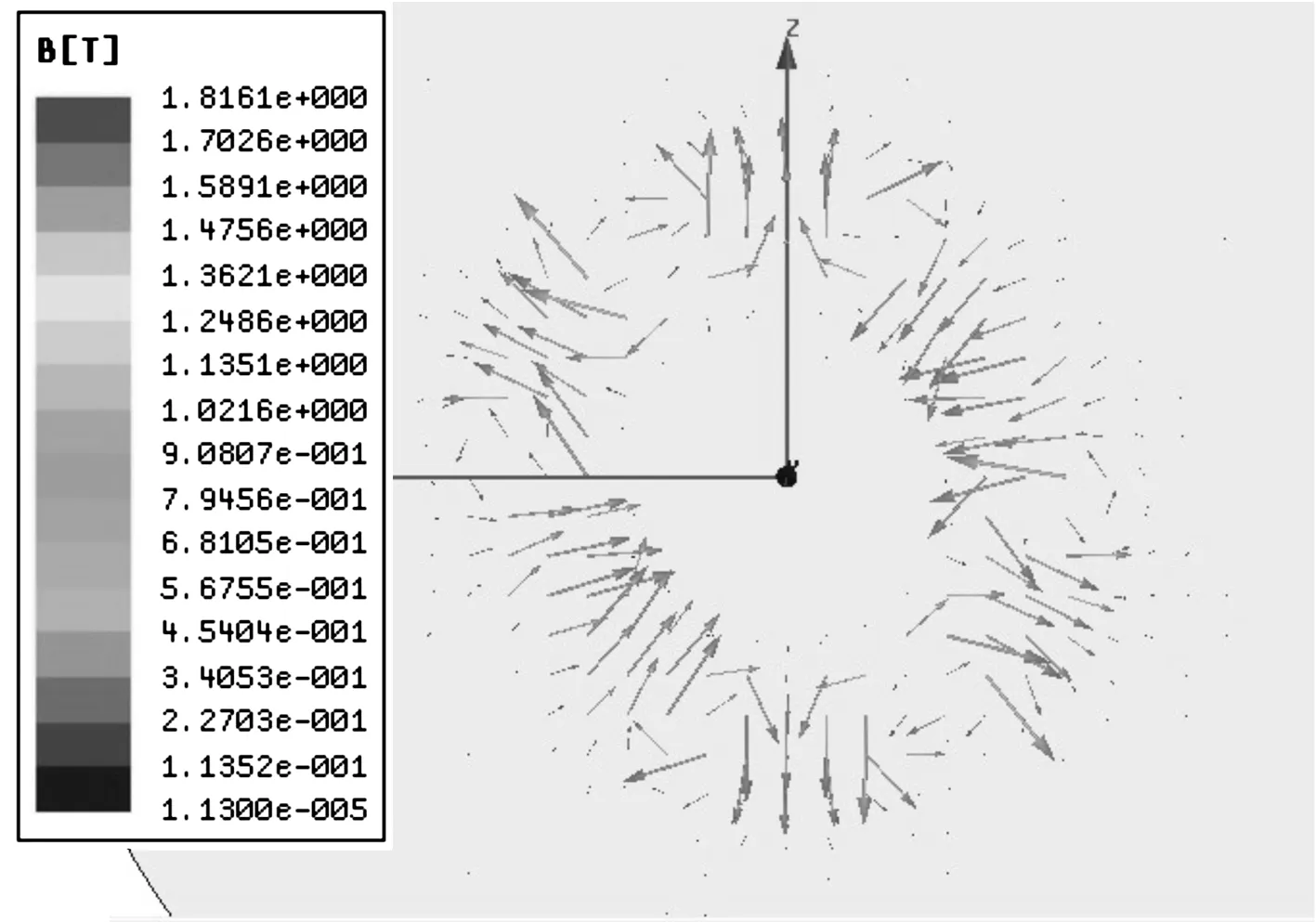
图9　球形永磁阵列稳态时磁感应线分布Fig.9 Distribution of magnetic induction line of the spherical magnet array at steady state

通过Ansoft Maxwell 3D有限元电磁瞬态仿真，得单个线圈以不同角速度绕球形永磁阵列一圈时线圈内产生的感应电动势。图10为角速度ω=4πrad/s时仿真所得线圈中感应电动势变化。经分析总结得不同角速度下解析法及仿真结果差异，见图11。

本文球形永磁阵列在经过圆心的截面上，轴、径向充磁磁铁不属于严格的对称分布，见图12，相邻3块永磁阵列构成磁铁回路，与图9磁感应线分布吻合。因此，动子永磁阵列相对定子线圈运动时3D瞬态仿真所得单个线圈内感应电动势未成严格的正弦变化，而在每个单独磁铁回路中成类似正弦变化(图10)。

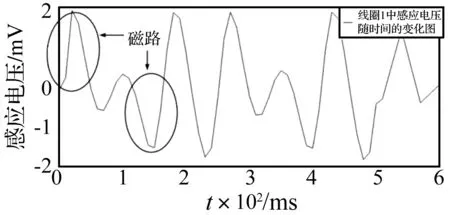
图10　线圈内感应电动势的变化图Fig.10 Changes of coil induction electromotive force

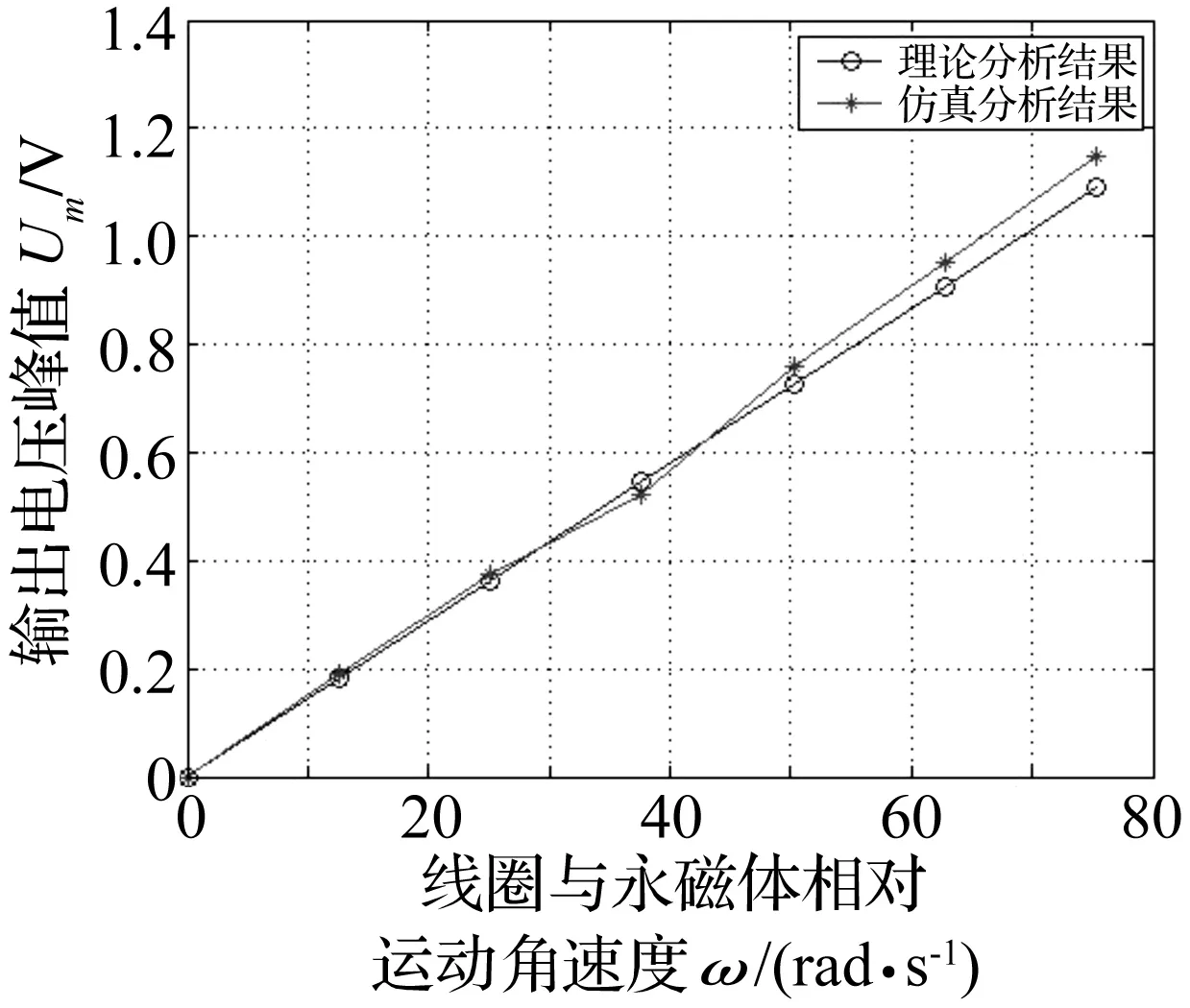
图11　不同角速度时解析法及仿真输出结果Fig.11 Output results of analytical method and simulation method under different angular velocity

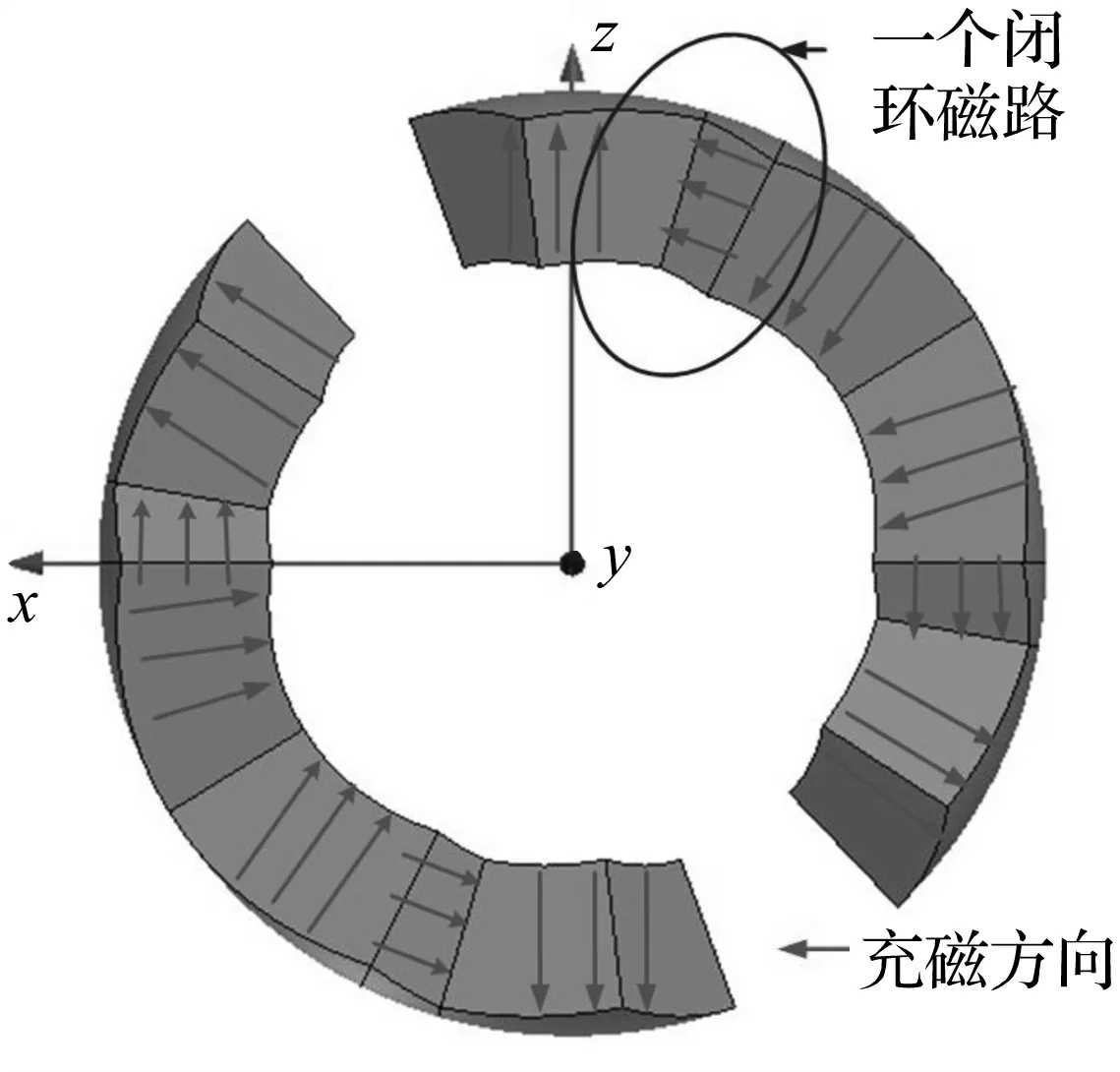
图12　磁铁回路示意图Fig.12 The diagram of magnet circle

将仿真所得线圈内感应电动势变化与计算结果比较知，两种方法所得结果近似相同，误差约5.56%。此误差因有限元网格剖分选择及解析计算忽略部分磁漏所致。

6实验性能测试

为测试该结构输出性能、验证其对多方向振动能回收的适应性，制作样机并搭建实验系统平台见图13。

图13　性能测试平台Fig.13 Performance test platform

实验性能测试系统中，由信号发生器产生所需频率及振幅信号，经功率放大器后给激振器模拟环境振动，其中激振器可调节激振方向模拟多方向激振效果；激光测距仪用于实时监测激振平台位移，通过后续PC机软件处理得激振平台振幅及加速度；示波器通过输出波形获得该样机的输出性能。实验测试结果为，激振方向为z轴(即空间中竖直方向)时。由调节信号发生器产生的信号频率可获得该结构开路电压与激振频率关系，见图14。由图14看出，激振为z轴方向、结构在频率10 Hz时单个线圈开路输出达最大，约250 mV。

为测试结构对多方向振动能收集特性，调节激振方向，获得该结构开路输出电压与激振方向关系曲线，见图15。由图15看出，结构在空间任意方向外激励下均能产生一定输出。水平激振时单个线圈开路输出电压最大，约400 mV。

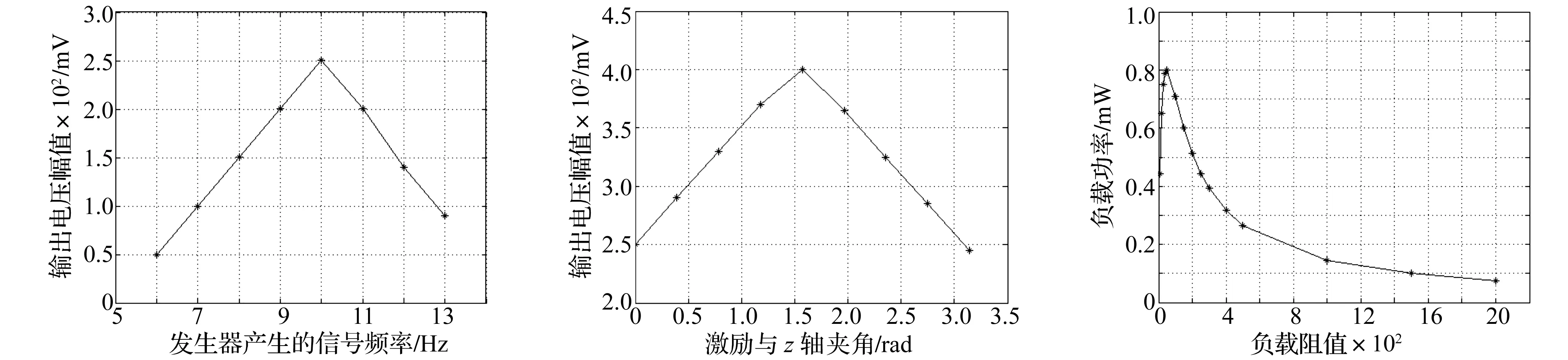
图14 开路电压与激振频率关系Fig.14Relationshipbetweenopen-circuitvoltageandexcitationfrequency图15 开路电压与激励方向关系Fig.15Relationshipbetweenopen-circuitvoltageandexcitationdirection图16 负载功率与负载阻值关系Fig.16Relationshipbetweenloadpowerandloadresistance

为更具体测试该结构输出性能接入负载，经测试、计算分析获得水平激振方向时结构负载功率与负载阻值关系曲线，见图16。由图16看出，负载功率随负载阻值增大先增大再减小，负载阻值约50 Ω时单个线圈负载功率达最大，约0.8 mW。实验测得该线圈阻值约47.8 Ω，与负载电阻与线圈内阻相匹配时负载功率达最大理论匹配。

7结论

(1) 本文设计的球形永磁阵列振动能量采集器能有效收集环境中任意方向振动能。利用Halbach阵列，据法拉第电磁感应定律推导模型工作时线圈气隙磁通及感应电动势解析公式，并据理论分析结果对模型进行参数优化设计。

(2) 模型性能测试表明，该模型能有效响应空间中任意方向振动，获得输出电能。外激励为10 Hz、水平激励方向、负载阻值50 Ω时该球形振动能量采集器输出电能达最大。该球形振动能量采集器对多方向环境振动适应性较好。本成果对多方向振动能量采集研究有一定指导意义。

参 考 文 献

[1] Guan M J, Liao W H. On the efficiencies of Piezoelectric energy harvesting circuits towards storage device voltages [J].Smart Materials and Structures, 2007, 16(2):498-505.

[2] 陈仁文.新型环境能量采集技术[M].北京:国防工业出版社,2011.

[3] 袁江波,谢涛,单小彪,等.压电俘能技术研究现状综述[J].振动与冲击,2009,28(10):36-42.

YUAN Jiang-bo, XIE Tao, SHAN Xiao-biao, et al. Piezoelectric status of Technology[J]. Piezoelectric Status of Technology, 2009,28(10):36-42.

[4] Mitcheson P D, Miao P, stark B H, et a1. MEMS Electrostatic micro power generator for low frequency operation[J].Sensors and Actuators A,2004,115(2/3):523-529.

[5] 李林,郭隐彪,陈旭远. 基于微机电系统的振动能量采集器件设计分析[J]. 机械工程学报,2009,45(9):238-242．

LI Lin, GUO Yin-biao, CHEN Xu-yuan. Design and analysis of vibration energy collector based on MEMS[J]. Journal of Mechanical Engineering, 2009, 45(9): 238-242.

[6] Wang P H, Dai X H, Fang D M, et a1. Design fabrication and performance of a new vibration-based electromagnetic micro power generator[J]. Microelectronics, 2007, 38(12): 1175-1180.

[7] Williams C W, Yates R B. Analysis of a micro-electric generator for Microsystems[J]. Sens Actuators A,1996, 52:8-11.

[8] Williams C W, Woods R C, Yates R B. Feasibility of a vibration powered micro-electric generator[C]//IEE Colloquium on Compact Power Sources,1996: 1-7.

[9] Perez-Rodriguez A, Serre C, Fondevilla N,et al. Design of electromagnetic inertial generators for energy scavenging applications proceedings of eurosensors XIX[C]//Barcelona, Spain, Paper MC5,2005.

[10] Beeby S P, Torah R N, Tudor M J,et al. A micro electromagnetic generator for vibration energy harvesting [J]. J. Micromech. Microeng,2007, 17: 1257-1265.

[11] Feenstra J, Granstrom J, Sodano H. Energy harvesting through a backpack employing a mechanically amplified-piezoelectric stack[J].Mechanical Systems and Signal Processing, 2008, 22(3): 721-734.

[12] Xue H, Hu Y T, Wang Q M. Broadband piezoelectric energy harvesting devices using multiple bimorphs with different operating frequencies[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2008, 55(9): 2104-2108.

[13] Erturk A, Renno J M, Inmall D J. Piezoelectric energy harvesting from a L-shaped beam-mass structure with an application to uAVs[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(5): 529-544.

[14] 刘祥建,陈仁文．Rainbow型压电换能结构的有限元分析与实验[J]．光学精密工程,20ll,19(4):789-796．

LIU Xiang-jian, CHEN Ren-wen. Finite element analysis and experiments on rainbow shape piezoelectric energy transferring elements[J].Optics and Precision Engineering,2011,19(4): 789-796.

[15] Halbach K. Design of permanent multipole magnets with oriented rare earth cobalt material[J]. Nuclear instruments and methods, 1980,169(1): 1-10.

[16] Raich H, Blümler P. Design and construction of a dipolar Halbach array with a homogeneous field from identical bar magnets: NMR mandhalas[J]. Concepts in Magnetic Resonance, 2004, 23(1): 16-25.

[17] Choi J S, Yoo J. Design of a halbach magnet array based on optimization techniques[J]. Magnetics, IEEE Transactions on, 2008, 44(10): 2361-2366.

收稿日期：2014-09-15修改稿收到日期：2015-01-20

通信作者陈仁文 男，教授，博士生导师，1966年1月生

中图分类号:TN384

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.02.036

Design and optimization of spherical magnet array structure of energy harvesting system

DING Zhi-qiang, CHEN Ren-wen, ZHANG Piao-yan, XIA Hua-kang, YANG Pei

(State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:A spherical electromagnet vibration energy harvester was designed to harvest multi-directional vibration energy. Based on the 2D Halbach array model, a novel sphere Halbach array was designed, which increases the magnetic field gradient in the coil as compared with the traditional permanent magnet array, so as to improve the output performance. The parameter optimization of the spherical structure was carried out according to the analytic results by using the corresponding mathematical model. The finite element simulation analysis and experimental performance test were carried out on the spherical structure model. The experiment results show that the new structure can respond to vibration from any direction, and then transfer the vibration energy to electricity. When the external excitation frequency is 10 Hz, the direction of excitation is horizontal and the load resistance is 50 Ω, the electricity output of this spherical vibration energy harvester reaches maximum. The maximum load power of a single coil is 0.8 mW.

Key words:vibration energy harvesting; electromagnetic; multi-direction; Halbach array; finite element

第一作者 丁志强 男，硕士生，1989年9月生

邮箱：rwchen@nuaa.edu.cn