排爆机械臂多目标轨迹规划研究
马振书, 张云峰, 孙华刚, 陆继山
(1.军械技术研究所,石家庄 050003;2.军械工程学院,石家庄 050003)
排爆机械臂多目标轨迹规划研究
马振书1, 张云峰2, 孙华刚1, 陆继山2
(1.军械技术研究所,石家庄050003;2.军械工程学院,石家庄050003)
摘要:针对排爆机械臂轨迹规划问题,提出多目标轨迹规划方法。建立三次样条曲线分段轨迹描述方程,采用外加虚拟点法保证三次样条曲线可任意指定轨迹初始速度、加速度,提出灵活性优化目标以提高机构灵活性;将优化目标及运动学约束以轨迹方程参数表示,转化为对各段运动时间的寻优;采用CNSGA-Ⅱ对排爆机械臂运动进行多目标轨迹优化,处理非线性约束最优化,建立排爆机械臂多目标轨迹规划算法流程。结果表明,该方法能有效提高规划结果灵活性,各项目标均优于线性加权单目标规划,所得轨迹平滑可控。
关键词:排爆机械臂;轨迹规划;多目标优化;NSGA-Ⅱ
排爆机器人(Explosive Ordnance Disposal Robot)指替人在爆炸等危险环境中完成任务的机器人[1]。大多数排爆机器人为遥控操作,通过监视器观察作业环境,操纵机械臂关节完成作业。此控制较易产生视觉疲劳,在精神高度紧张下较难精确控制机械臂,易引发爆炸等危险。因此,自主决策、运动的排爆机器人成为发展方向[2-4]。排爆机械臂为排爆机器人的作业部分,其轨迹规划为排爆机器人性能的关键因素,决定排爆机械臂的运动方式。
轨迹规划为机器人学的基本问题,其任务即据路径规划结果产生随时间连续变化的各关节运动律。机器人轨迹规划主要有笛卡尔空间规划[5-6]及关节空间规划[7-9],前者形象直观,但要实现快速逆运动学计算,运动轨迹可能穿过奇异区域[10];而关节空间规划优点在于控制系统直接作用于关节,易满足设计要求及运动约束,避免奇点、关节突变,减少正逆运动学计算[11]。轨迹规划基本的优化条件为最小执行时间[12-13]、最小能量[14]及最小脉动[15-16],大多混合优化方法均基于此。Gasparetto等[17]以时间-脉动最优为目标,研究该优化条件对机械臂运动性能影响,经与传统的时间最优对比表明,该方法能有效减小关节脉动,减小机械磨损及振动,使机器人运动性能更好。庞慧[18]提出的基于三次样条插值的时间最优轨迹规划方法,能初步解决排爆机械臂轨迹规划问题,但仍有待进一步解决的问题,即① 轨迹规划目标中未考虑机械臂的灵活性,实际应用中若机械臂在某位置灵活性较低,其末端微小运动会导致关节速度突然变化。② 混合目标优化各目标间相互冲突,其权值靠经验设定,对结果影响较大;多目标优化方法并未给出从Pareto解集中选择最优解方法;传统NSGA-Ⅱ较难处理复杂非线性约束组优化问题。③ 经典三次样条插值无法同时保证第一、二类初始条件,高次样条曲线构造复杂,龙格现象明显。
为此,本文以某型排爆机器人二代样机为原型,研究其排爆机械臂多目标轨迹规划技术。在优化目标中加入灵活性函数,使轨迹规划结果易于跟踪;采用改进三次样条曲线在过渡点间插值,使机械臂轨迹满足任意初始条件;用NSGA-Ⅱ算法轨迹规划获得满足多约束条件、多优化目标的Pareto解集,并提出最优解选择方法。
1排爆机械臂结构及灵活性
1.1机械臂结构
排爆机械臂结构见图1,机械臂有六个自由度,即腰部回转、大臂俯仰、小臂俯仰、小臂伸缩、手腕俯仰及手腕旋转。建立D-H坐标系,参数见表1。工作空间末端位姿与关节空间坐标可通过齐次变换矩阵相互转化。机械臂由电液混合驱动,机构复杂,对轨迹平滑度要求较高;排爆机器人能源来自蓄电池,能耗低的工作轨迹可增加排爆机器人续航能力。

图1 排爆机械臂结构Fig.1 Structure of explosive ordnance disposal manipulator

#θdaα0-1θ1(90)00-901-2θ2(-90)0a202-3θ3(0)0a3-903-40d40904-5θ5(0)00-905-6θ6(0)000
1.2机械臂灵活性
引起机械臂末端特定的关节空间运动需用雅克比矩阵计算。雅克比矩阵为奇异矩阵或机械臂运动到变化范围极限时,其末端微小运动会导致关节速度突然变化,此时对应的机械臂位形称奇异位形。
图2为机械臂前三个关节的速度椭圆,椭圆半径越短机械臂末端越难实现与该半径对应方向的运动[19]。图2(a)为正常位姿的速度椭圆,图2(b)为接近奇异位形的速度椭圆。可见,当机械臂接近奇异位形时其末端失去某些方向的灵活性,严重影响机械臂关节速率的控制效果。

图2 机械臂末端速度椭圆Fig.2 End-effector velocity ellipsoids
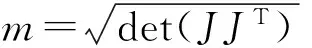
排爆机器人抓取重量大,工作环境危险,一旦机械臂失控会导致事故发生,因此其轨迹规划须避开奇异位形附近区域,保证机械臂灵活可控。
2多目标轨迹规划问题构造
关节空间轨迹规划以工作空间路径的点经逆运动学计算所得关节变量值作为过渡点,过渡点间采用插值函数构造排爆机械臂运动轨迹。
2.1改进三次插值函数
为满足速度、加速度连续性要求,用三次样条函数对过渡点插值。传统三次样条插值无法同时满足第一、二类边界条件,文献[8]的改进方法虽能使轨迹始末速度、加速度同时为零,但不能任意指定采用始末速度、加速度,不适用于实时轨迹规划。本文用在第二及倒数第二位置添加两个虚拟点方式改进三次样条函数。设N关节机械臂工作有n-2个路径点,加两个虚拟点,每个关节有n个过渡点。
三次样条曲线加速度为线性函数,因此关节j在第i段加速度函数Wj,i(t)计算式为
(1)
式中:wj,i为关节j在第i过渡点处加速度;hi=ti+1-ti为通过相邻过渡点所用时间;ti为轨迹通过第i过渡点时刻。
对式(1)积分两次消去任意常数,得位移公式为

(i=1…n-1,j=1…N)
(2)
式中:Qj,i(t)为关节j在第i段位移函数;qj,i为关节j在第i过渡点处位移。
对式(2)求导得速度公式为
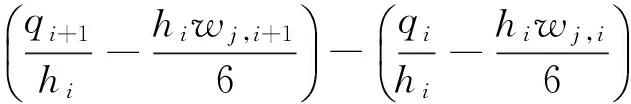
(i=1…n-1,j=1…N)
(3)
式中:Vj,i(t)为关节j在第i段的速度函数。
式(3)代入连续性条件,得
Vj,i(ti-0)=Vj,i+1(ti+0)
(4)
整理得
uiwj,i-1+2wj,i+(1-ui)wj,i+1=di,
(i=2,5,…,n-1,j=1…N)
(5)
为使机械臂能实时规划含任意初始速度、加速度的运动轨迹,虚拟过渡点位置公式为
(6)
qj,n-1=qj,n-hn-1vj,n+
(7)
最终获得求过渡点处加速度线性方程组,系数矩阵为严格对角占优的三对角阵,故方程组有解,已知wj,1,wj,n,vj,1,vj,n,qj,i,hi的值即可求得过渡点处加速度wj,i,即

2.2轨迹规划目标
针对排爆机械臂轨迹规划问题,提出4个轨迹规划目标,分别为执行时间、脉动目标、加速度目标及机械臂灵活性,以此满足排爆机械臂对工作效率、轨迹平滑度、能量消耗及机械臂灵活性要求。据三次样条曲线构造目标函数,表达式分别为
(9)
(10)
(11)
(12)
式(9)~(13)中:J为机械臂雅克比矩阵;VCj,ACj,JCj为关节j的速度、加速度及脉动约束;Hlb为各段运动时间下限。
(13)
由以上推导过程知,机械臂最优轨迹规划问题转为在非线性约束下对各段运动时间hi的多目标优化问题。式(9)为执行时间目标函数,以过渡点间运动时间之和表示,目的为减小机械臂运动时间;式(10)为轨迹脉动目标函数,以各过渡点间脉动平方和表示,目的为使运动轨迹更平滑,减小加速度突然变化;式(11)为加速度目标函数,目的为减小机械臂运动过程中加速度,进而减小能量消耗;式(12)为机械臂灵活性目标函数,可增加机械臂运动中的灵活性,使运动轨迹远离奇点;式(13)为约束条件,依次为速度约束、加速度约束、脉动约束、时间约束。传统单目标轨迹规划方法的目标函数表达式为
(14)
式中:k1,k2,k3,k4为权重系数;N1,N2,N3,N4为归一化参数。
优化结果取决于凭直觉及先验知识设置的权重系数,较难获得多目标优化条件的近似最优解。
3非支配排序遗传算法(NSGA-Ⅱ)
传统线性加权多目标优化方法各优化目标间相互冲突,优化结果过度依赖人为设置的权重系数。而基于非支配排序的多目标优化方法可较好的解决此问题。对多目标优化问题,一般无法找到使所有目标最优的解,因此引入非次解概念。非次解指无法在改进一个目标函数的同时不削弱其它目标的解,基于非次解的多目标优化亦称Pareto最优化。
NSGA-Ⅱ(Nondominated Sorting Genetic Algorithm)为由Deb等[20]提出基于Pareto的多目标进化算法,其结果能较好逼近Pareto前沿,能有效解决多目标优化问题。较NSGA,NSGA-Ⅱ引入精英机制,保留前代优秀个体,并用快速非支配排序,算法复杂度由O(mN3)降为O(mN2),其中m为优化目标数,N为种群数;NSGA-Ⅱ无需设置主观可调参数,能消除共享参数对算法效果影响。因此,NSGA-Ⅱ在收敛性(更接近真实Pareto前沿)及多样性(结果分布性好)均优于其它多目标优化算法。
3.1约束非支配排序遗传算法(CNSGA-Ⅱ)
传统NSGA-Ⅱ难以处理含复杂非线性约束的多目标最优化问题,本文对其进行改进。
为维持NSGA-Ⅱ流程的模块性,改变个体i,j支配关系,定义若以下任一条件成立,则个体i约束-支配个体j:①i满足约束条件而j不满足约束条件;②i、j均不满足约束条件,但i拥有较小的约束超越量;③i、j均满足约束条件,且i支配j。
个体约束超越量计算式为
(15)
式中:m为非线性约束数量;n为线性约束数量;h为个体;Cv为个体h约束超越量,非线性约束nc及线性约束lc被转化为不等式形式,若个体在约束范围内则Cv=0。
CNSGA-Ⅱ不改变算法的复杂度,无需增加惩罚函数,只改变支配关系定义,使符合约束条件或约束超越小的个体支配不符合约束条件或约束超越大的个体,其它过程与传统NSGA-Ⅱ相同。
3.2多目标轨迹规划流程
CNSGA-Ⅱ算法求解排爆机械臂多目标轨迹规划问题算法流程见图3。其中选择算子为随机遍历抽样;交叉算子为独立点交叉;变异算子为高斯变异。

图3 多目标轨迹规划算法流程Fig.3 Process of multi-objective trajectory planning algorithm
4仿真与分析
用CNSGA-Ⅱ规划排爆机械臂运动轨迹。机械臂运动所经关节位置序列见表3,各关节运动学约束见表4。以改进三次样条曲线对过渡点间轨迹插值,设始末速度、加速度均为零,种群规模为500,各段运动时间上限由经验给出,下限计算式为
(16)
式中:v,w,j为以Hlb各段运动时间所得速度、加速度、脉动。

表3 轨迹规划输入

表4 关节运动学约束
图4为多目标轨迹规划所得Pareto前沿,图4为加入灵活性目标后的优化结果。其中图4(b)未加入灵活性目标,可见两条曲线形状发生明显变化,因轨迹规划结果会过于靠近奇点,导致机械臂失去灵活性及可操纵性。

图4 Pareto前沿Fig.4 Pareto front
表5、6分别为不考虑、考虑灵活性的多目标表优化所得Pareto最优解中单一目标最优个体目标值。对比看出,加入灵活性最优条件使机械臂灵活性有所提高,但会牺牲时间最优目标。由雅克比矩阵定义,机械臂轨迹绕过低灵活性区域需增加运动时间,因此目标对执行时间影响较大,而对脉动目标、加速度目标影响较小。
据混合优化目标式(14),令N1=40,N2=0.001,N3=0.01,N4=0.000 01,k1=0.4,k2=0.2,k3=0.2,k4=0.2;其中归一化系数N1,…,N4由单一目标优化结果获得,权重系数k1,…,k4据实际经验取得。用经典遗传算法进行传统单目标轨迹规划,与多目标轨迹规划所得Pareto解集中时间目标最接近的解对比,结果见表7。由表7看出,时间相同时Pareto最优解的脉动、加速度、灵活性目标均远优于传统混合单目标优化,表明多目标优化结果较好逼近Pareto前沿。
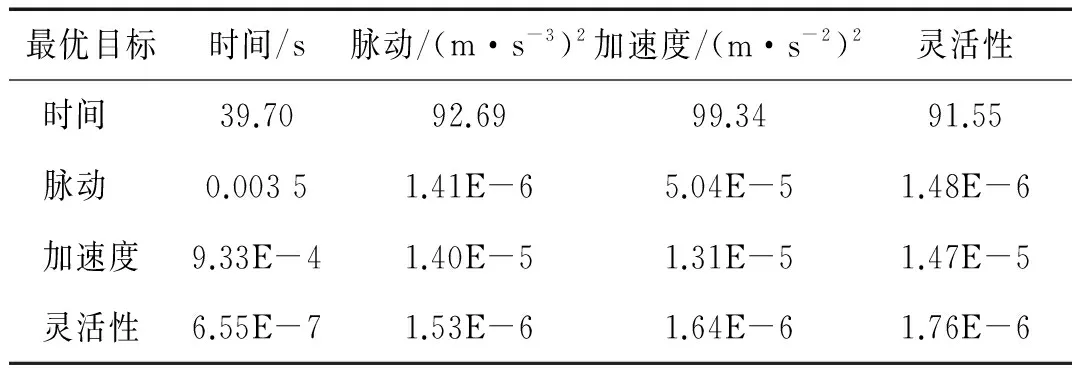
表5 多目标优化结果
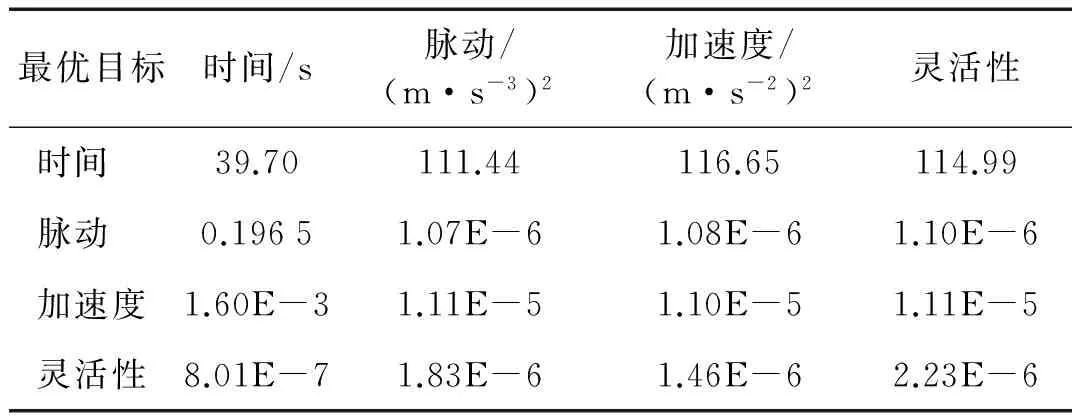
表6 考虑灵活性的多目标优化结果

表7 优化结果比较
多目标轨迹规划所得结果为一组近似Pareto最优解,因此用平均最优解从Pareto解集中选最优解。表达式为
(16)
式中:Fmean为平均最优解;Objmax,Objmin分别为一组Pareto最优解中某优化目标最大、最小值,可选使Fmean值最小的解作为多目标轨迹规划最终结果。
图5~图8为平均最优解与采用传统GA法所得位移、速度、加速度及脉动曲线。图中实线为多目标优化结果,虚线为传统线性加权法优化结果。可见位移、速度、加速度曲线平滑连续,各曲线变化范围均在运动学约束内,满足工作、设计要求。除关节5外,其它各关节虚线变化幅度均大于实线,表明同等运动时间下,

图5 各关节位移Fig.5 Displacement of joints

图6 各关节速度Fig.6 Velocity of joint

图7 各关节加速度Fig.7 Acceleration of joints

图8 各关节脉动Fig.8 Jerk of joints
多目标轨迹规划的关节空间轨迹更平滑,可减小机械磨损与多余振动;优化时考虑机构灵活性,使机械臂易于跟踪运动轨迹,该运动律可直接作为控制器输入引导机械臂运动。
5结论
(1) 利用基于改进三次样条插值及CNSAGA-Ⅱ多目标轨迹规划方法,所得排爆机械臂运动轨迹平滑,较好满足排爆机械臂动作时避免加速度突变、减小消耗能量要求。通过在目标函数中加入机构灵活性指标,能提高轨迹规划结果的灵活性、便于机械臂跟踪规划轨迹,轨迹灵活性高也可提高机构的控制性能。
(2) 多目标优化的结果为Pareto解集,较难从中选择某个合适的解。平均最优解通过多目标归一化加合方式选择最优解,避免结果选择的盲目性。本文所提算法可应用于其它类型串联机械臂系统的轨迹规划。
参 考 文 献
[1] 范路桥,姚锡凡,祁亨年,等.排爆机器人的研究现状及其关键技术[J].机床与液压,2008,36(6):139-143.
FAN Lu-qiao, YAO Xi-fan, QI Heng-nian, et al. Research progress and key techniques of explosive ordnance disposal robot[J].Machinetool & Hydraulics,2008,36(6):139-143.
[2] 范路桥,姚锡凡,蒋梁中,等.半智能排爆机器人的单手双目手眼系统[J].华南理工大学学报:自然科学版,2008,36(4): 40-44.
FAN Lu-qiao,YAO Xi-fan,JIANG Liang-zhong,et al. Single-hand and binocular eye-in-hand system for semi-intelligent EOD robot[J]. Journal of South China University of Technology :Natural Science Edition,2008,36(4):40-44.
[3] 申加刚,董再励,郝颖明,等.排爆作业机器人模拟训练系统研究[J].机器人,2005,27(5):426-430.
SHEN Jia-gang, DONG Zai-li, HAO Ying-ming, et al. Research on a virtual training simulator for explosive-handling Robot[J].Robot, 2005,27(5):426-430.
[4] 曾建军,杨汝清,张伟军.有限人参与下的排爆机器人半自主抓取[J].上海交通大学学报,2007,41(8):1238-1342.
ZENG Jian-jun, YANG Ru-qing, ZHANG Wei-jun. Research of semi-automatic bomb fetching with limited support of human in explosive ordnance disposal robot[J]. Journal of Shanghai Jiaotong University, 2007,41(8):1238-1342.
[5] 陈国梁,王心汉,王敏.机械手圆周运动的轨迹规划与实现[J].华中科技大学学报:自然科学版,2005,33(11):63-66.
CHEN Guo-liang, WANG Xin-han, WANG Min. Trajectory planning for the circular motion of manipulator and its implementation[J]. J.Huazhong Univ. of Sci. & Tech.:Nature Science Edition,2005,33(11):63-66.
[6] 任敬轶,孙汉旭.一种新颖的笛卡尔空间轨迹规划方法[J].机器人,2002,24(3):217-221.
REN Jing-yi, SUN Han-xu.A novel method of trajectory planning in cartesian space[J].Robot,2002,24(3):217-221.
[7] Solteiro Pires E J, de Moura Oliveira P B, Tenreiro Machado J A.Manipulator trajectory planning using a MOEA[J]. Applied Soft Computing,2007(7):659-667.
[8] Gasparetto A, Zanotto V. A technique for time-jerk optimal planning of robot trajectories[J]. Robotics and Computer-Integrated Manufacturing,2008(24):415-426.
[9] Rossi C, Savino S. Robot trajectory planning by assigning positions and tangential velocities[J]. Robotics and Computer-Integrated Manufacturing, 2013 (29):139-156.
[10] Niku S B.孙富春,朱纪洪,刘国栋,等,译.机器人学导论 分析、控制及应用[M].2版.北京:电子工业出版社,2013.
[11] Gasparetto A, Zanotto V. Optimal trajectory planning for industrial robots[J]. Advances in Engineering Software, 2010(41):548-556.
[12] Shiller Z, Chang H, Wong V. The practical implementa- tion of time-optimal control for robotic manipulators[J]. Robotics & Computer-Integreted Manufacturing,1996,12(1):29-39.
[13] Lee Y D, Lee B H, Kim H G. An evolutionary approach for time optimal trajectory planning of a robotic manipulator [J].Information Science,1999(113):245-260.
[14] Oen K T, Wang L C T. Optimal dynamic trajectory planning for linearly actuated platform type parallel manipulators having task space redundant degree of freedom [J]. Mechanism and Machine Theory,2007(42): 727-750.
[15] Boscariol P, Gasparetto A. Model-based trajectory planning for flexible-link mechanisms with bounded jerk[J]. Robotics and Computer-Integrated Manufacturing, 2013(29): 90-99.
[16] Gasparetto A, Zanotto V. A new method for smooth trajectory planning of robot manipulators[J]. Mechanism and Machine Theory,2007 (42):455-471.
[17] Gasparetto A, Lanzutti A, Vidoni R, et al. Experimental validation and comparative analysis of optimal time-jerk algorithms for trajectory planning[J]. Robotics and Computer-Integrated Manufacturing, 2012(28):164-181.
[18] 庞慧.危险弹药处理机器人工作装置的性能分析及优化[D].天津:河北工业大学,2010.
[19] Corke P. Robotics, vision and control[M]. Berlin: Springer, 2011.
[20] Deb K, Agrawal S, Pratap A, et al. A fast elitist nondominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[J]. Evolutionary Computation, 2002,6(2):182-197.
基金项目:国家863项目(2001AA422420)
收稿日期:2014-12-16修改稿收到日期:2015-01-30
通信作者张云峰 男,硕士生,1990年生
中图分类号:TP241.3
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.02.019
Multi-objective trajectory planning of explosive ordnance displosal manipulators
MA Zhen-shu1, ZHANG Yun-feng2, SUN Hua-gang1, LU Ji-shan2
(1. Institute of Mechanical Technology, Shijiazhuang 050003, China; 2. Mechanical Engineering College, Shijiazhuang 050003, China)
Abstract:A multi-ojective optimization technique was presented to solve the problem of explosive ordnance displosal manipulators’ trajectory planning. Cubic splines were used to connect each pair of consecutive via-points. Two virtual points were introduced to ensure the initial and final conditions of velocity and acceleration to be respected. A manipulability optimization objective was developed to enhance the manipulability of mechanism. The objective functions and kinematic constraints were described by the parameters of cubic splines, so that the problem was transformed into the optimization of each time interval. The constraint NSGA-Ⅱ was adopted to plan the multi-objective trajectory, which is suitable to solve optimization problems with nonlinear constraints. The procedure of the algorithm based on NSGA-Ⅱ was created. Comparing with the traditional method, the simulation results indicate that the developed technique can improve the manipulability effectively and every optimization index achieved is better than the results of linear weighting coefficient technique. The obtained trajectories are smooth enough and easy to control.
Key words:explosive ordnance displosal manipulator; trajectory planning; multi-objective optimization; NSGA-Ⅱ
第一作者 马振书 男,博士,研究员,1966年生

