基于拟静态初值的载荷识别数值修正算法
徐 菁, 张 方, 姜金辉, 浦玉学, 蒋 祺
(南京航空航天大学 航空宇航学院 机械结构力学及控制国家重点实验室,南京 210016)
基于拟静态初值的载荷识别数值修正算法
徐菁, 张方, 姜金辉, 浦玉学, 蒋祺
(南京航空航天大学 航空宇航学院 机械结构力学及控制国家重点实验室,南京210016)
摘要:推导拟静态法获得载荷初值及稳定不发散计算结果,分析获得初值不准确原因,推导获得新的载荷识别方法。该方法基于数值原理,利用步步修正达到减少累积误差效果,可较大程度提高计算稳定性,并将数值迭代修正方法用于有限元模型载荷识别。结果表明,该方法能较准确识别出工程中常见的多种载荷,并具有一定抗噪能力。
关键词:载荷识别;时域;拟静态法;数值修正
动载荷识别技术为结构动态设计关键,属于结构动力学第二类逆问题。其原理为据已知系统特性及动响应求得结构所受动载荷。研究内容为加载位置识别及动载荷量值识别。目前,动载荷识别技术主要有频、时域两类方法,其中时域法可直观表现载荷随时间历程的变化规律。
张方等[1-2]利用广义正交多项式导出基于多节点时间有限元的载荷识别模型,将广义正交域线性算子逆运算替代时域的复杂逆卷积关系,通过计算正交多项式系数求解载荷,使复杂结构分布动态载荷识别问题得以解决。Nordstrǒm等[3]采用时延方法将载荷识别过程中存在的不适定问题转化为适定问题,研究时间延迟选取对激励力识别精度影响。Hashemi等[4]为识别施加于简支梁的动载荷引入遗传算法,仿真结果表明该方法的正确性及对测量噪声、传感器位置的鲁棒性。Gunawan等[5]采用正则化二次样条函数拟合系统冲击载荷,利用基于L曲线的TSVD方法求解动态载荷。该方法虽能提供较精确的载荷识别结果,但不能准确识别冲击载荷卸载过程。Kazemi等[6]利用应变响应时间积分识别动载荷。结果表明,用应变识别的载荷波动较大,需用正则化方法修正,且结果对测试噪声较敏感。韩旭等[7]将动态载荷表示为一系列脉冲或阶跃函数的叠加,并用零相位滤波器、正则化技术及优化策略实现载荷的稳定重构。郭杏林等[8]针对结构受多点分布载荷识别问题提出精细正则化算法,对载荷识别求解过程中的方程病态问题用正则化奇异值分解技术进行处理。姜金辉等[9-10]研究基于Wilson-θ反分析法的动载荷时域识别方法及θ取值、时间间隔、阻尼比、测量点位置数目及采样中噪声干扰等因素对动载荷识别精度影响,并在Wilson-θ反分析法基础上提出多种修正方案,使计算结果趋于收敛。朱涛等[11]引入Newmark积分获得系统离散运动方程,并基于动态规划法及Bellman最优化原理,推导出动态优化载荷识别算法公式,该方法抗噪性能较好。王静等[12]利用系统响应构造状态空间方程组,建立精确非递推连锁计算格式的时域内动载荷反演模型,通过正则化技术克服模型算子的病态特性及响应测量中噪声不利影响。
本文通过拟静态法获得不发散的识别力初值,并说明改初值偏离真实载荷原因。在此基础上推导获得基于数值迭代的修正算法并推广到多输入模型;用仿真算例及实验考察该算法的收敛性及抗噪能力。
1拟静态法获得初值
用数值迭代算法前提之一需获得可靠初值范围,此范围须含真实值且大小合适。本文所用拟静态载荷法即为能方便获得初值方法,计算过程简单,结果不发散。
加速度信号为工程中载荷识别常见输入形式,Wilson-θ法计算由加载力得到加速度响应时具有良好的数值稳定性。取θ>1.37即可保证结果无条件收敛,本文取θ=1.4,结合Wilson-θ法,可推导出拟静态法求载荷公式。对离散多自由度系统,动力学平衡方程为

(1)
在Wilson-θ法计算中[13],设外力在t~θΔt时间内线性变化,则有
f(t~θΔt)=f(t)+θ(f(t+Δt)-f(t))
(2)
由此,可得t+θΔt时刻系统等效静力方程为

(3)
(i=1,2,…,n)
(4)


(5)
求解上式可得di(t+θΔt),再据式(4),式(3)的解满足线性关系,即
(6)
设有m个测点,若已测出加速度响应,据Wilson-θ法假设,有

(7)

(8)
(9)

(10)
该方程组的解可分为3种情况:①m≤n即测点数小于未知载荷数时不能得到唯一解,无法识别;②m=n时可求得唯一解;③m≥n时对位移矩阵求广义逆,可得一组最小二乘解。
求出{λ}t+θΔt后,据式(4)可求出t+θΔt时刻动载荷值fi(t+θΔt),由于上一步载荷fi(t)已知,故可识别出下一步载荷为
fi(t+Δt)=
[fi(t+θΔt)-fi(t)]/[θ+fi(t)]
(11)
2数值迭代修正算法
拟静态法计算简便,虽对已知加速度响应求解所得载荷计算结果不会发散,但假定结构处于静载荷状态,独立计算每个时间间隔点,未考虑一个时间步长内前一时间点载荷、响应对后一时间点响应影响,故不适用于动载荷识别问题。
为进一步获得较精确结果,可用数值迭代修正拟静态法求得载荷初值,使每个时间间隔点载荷更接近真实载荷。其中,二分法与黄金分割法为常用数值迭代算法。由Wilson-θ法知
(12)
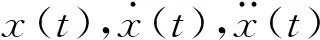
(12)化简为
(13)
若在第b1,…,bi,…bn自由度上施加载荷,在第a1,…,aj,…,am自由度上测量响应加速度,则有
f(t+Δt)={0,…,0,f(t+Δt)b1,0,…,0,f(t+Δt)bj,
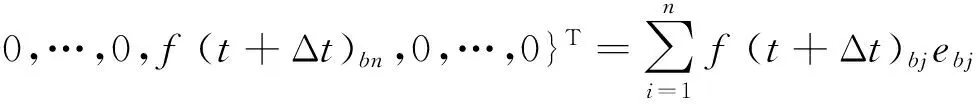
(15)
即
⋮
⋮
简写为
(16)
在该方程组中取n个方程,得
(17)
解方程,消去未知量,只保留f1得
(18)
式中:Ai1为系数矩阵去掉第i行第1列代数余子式;其余未知量用f1表示,则有
(19)
式中:Ain,1j为系数矩阵去掉第i、n行第1、j列代数余子式。令
(20)
对g(f1)求导,即
(21)
由拟静态法获得识别载荷的初始时间序列f(t)。设时间点tm对应的力为f(tm),令a0=-rf(tm),b0=rf(tm),r为区间放大倍数,且能满足g(a0)g(b0)<0,则[a0,b0]为初始含根区间(设f(tm)>0)。据单调函数性质知,此区间内g(f1)零点即为真实载荷。一般,若已获得含根区间[ak,bk](k=1,2,…),则令
(22)
用二分法[14]计算时取q=0.5;用黄金分割法计算则q=0.618,若

(23)
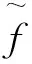
(24)
实际计算中所用终止原则为bk-ak≤10-p,p为正整数,有
ε≤(1-q)(bk-ak)=10-p(1-q)
(25)
式(24)可化为
(26)
求解以上不等式得
(27)
所需迭代步数上限为
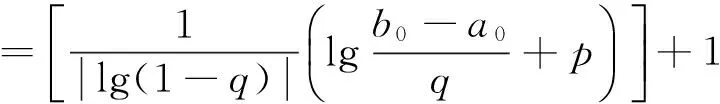
(28)
式中:[ ]为取整。
可见,步步迭代算法增加的计算量主要取决于每次K*的大小。因此确定所用迭代法后,计算耗时与初始含根区间边界值a0,b0及精度要求p密切相关,而结果的精确性主要由p决定。
3仿真计算
建立自由-自由梁矩形截面梁计算模型,梁长2 m,截面0.08 m×0.02 m,各阶阻尼比0.02,弹性模量72 GPa,材料密度2 700kg/m3,划分为20个有限元单元,每节点有平动、转动2个自由度,共42个自由度。结构单元节点示意见图1。

图1 结构单元节点示意图Fig.1 Diagram of structure elements and nodes
3.1算例1
在第29、33自由度分别加载f1=10sin(4πt)N,f2=15sin(8πt)N的正弦力。已知数据为第15、21、35自由度的加速度响应。无噪声下,取Δt=0.001 s,识别结果见图2。图2(a)为静态拟合算法所得识别力,可见,此拟合算法虽不能获得准确载荷,但结果未现发散且能稳定在一范围内,符合数值迭代修正的初值要求。图2(b)为修正后的识别力,故在精度要求合适前提下,数值迭代算法可获得较准确的计算载荷。
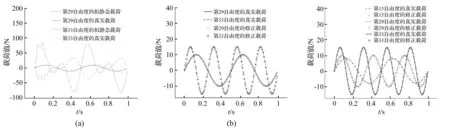

图2 二输入载荷识别对比图Fig.2Two-inputloadidentification图3 三输入载荷识别对比图Fig.3Three-inputloadidentification
3.2算例2
在上算例基础上增加一输入载荷,所测加速度响应增加到5个,即第15、29、33自由度上分别加载f1=8sin(4πt)N,f2=10sin(6πt)N,f3=15sin(8πt)N的正弦力,已知数据为第11、17、21、35、39自由度的加速度响应。3个输入载荷对比见图3。
实际问题中往往所遇为非规则正弦加载。对以上算例3个自由度的工程常见集中载荷,考察数值迭代修正法的识别效果。图4(a)为在第15、29、33自由度上加载半正弦、三角波及方波载荷,图4(b)为在第15、29、33自由度上加载锯齿波、组合正弦及冲击载荷。由图4知,该加载下结果均未发散,说明此算法对各种载荷具有良好的适应性及收敛性。
工程中噪声影响不可忽略,具不具备良好抗噪性能是判断算法稳定与否的重要依据。为验证数值修正算法的抗噪性能,在两算例正弦输入下,对已知加速度响应加入5%高斯白噪声。图5(a)、(b)分别为二、三输入下数值迭代修正算法识别结果。由图5看出,修正后识别曲线虽与真实结果存在一定偏离,但整体并未出现发散,能基本体现真实加载。
4实验验证
实验模型采用仿真计算的自由-自由梁,将其划分为20个有限元单元。
主要仪器设备有:NI PXI-4496机箱,NI USB-4431数据采集卡,PCB模态力锤,ICP型加速度传感器及连接线等。将实验梁用橡皮绳悬挂于支架上,实验装置见图6。
利用m+p SmartOffice软件进行模态实验,获得梁前几阶固有频率及阻尼比。建立梁仿真模型、计算固有频率,并用实验数据对仿真模型进行修正,使两者尽量吻合,弹性模量为68 GPa,材料密度2 700kg/m3,模型参数见表1。
用力锤快速敲击实验梁,利用Labview Signal Express软件采集数据,获得固定位置加速度响应。用其作为修正模型的加载响应,利用数值修正算法回推计算输入载荷,对比实验所测得真实输入载荷,分析算法的可行性。

图4 多形式加载识别对比图Fig.4 The identification in multiple types of load

图5 加噪后的识别结果图Fig.5 The identification after adding noise

参数第1阶第2阶第3阶第4阶第5阶第6阶第7阶第8阶第9阶固有频率/Hz实验值25.771.7141.4235.1348.3486.1645.7828.81032.2计算值25.771.1139.4230.5344.3481.1640.8823.71031.1 模态阻尼比/%2.5011.2870.4552.0470.2210.1680.1580.1590.164

图6 实验装置Fig.6 Experimental setup figure
取第7、15号节点为锤击加载点,第5、13号节点为响应采集点,采样率20 kHz。据加速度与模型参数,用数值修正算法计算获得冲击载荷曲线,见图7。
设fpeak为加载峰值,进一步分析实验结果数据,引入峰值误差参考量Epeak
(29)
实验中,Epeak,1=4.12%,Epeak,2=3.24%。
由图7及误差看出,识别曲线基本能反映真实加载趋势。冲击载荷加、卸载过程虽曲线平直段误差较大,但总体未现发散趋势。实验中造成误差原因较多,如梁的有限元模型与实际模型并不完全一致。实验仪器设备亦存在不稳定及固有误差,且锤击点亦会有偏离。
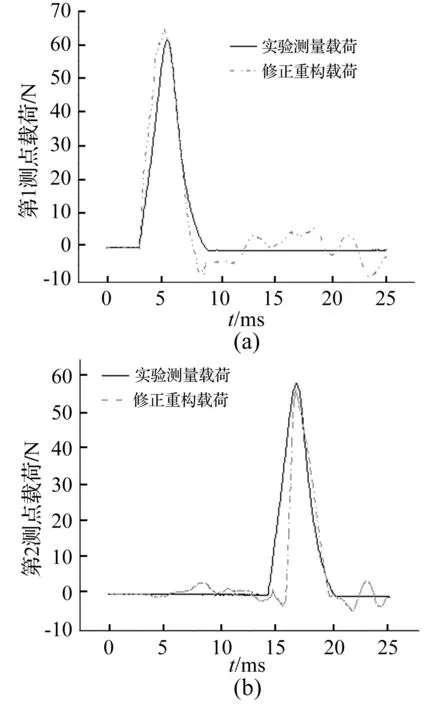
图7 实验结果曲线Fig.7 The identified curve of experimental result
5结论
载荷识别计算过程中,误差累积导致的发散难以克服。对此,本文提出载荷识别的新思路,在每个时间步长内利用数值算法进行迭代修正。仿真、实验结果表明,该修正算法可有效获得稳定的识别结果,基本收敛于真实加载。
参 考 文 献
[1] 张方,朱德懋. 基于广义正交域的一种动载荷识别方法研究[J].南京航空航天大学学报, 1996, 9(1):1-8.
ZHANG Fang, ZHU De-mao. A new theoretical study of dynamic load identification based on generalized polynomial expansion[J]. Journal of Nanjing University of Aeronautics & Astronautics, 1996, 9(1):1-8.
[2] 张方,秦远田,邓吉宏. 复杂动态载荷识别技术研究[J].振动工程学报, 2006, 19 (1): 81-85.
ZHANG Fang, QIN Yuan-tian, DENG Ji-hong. Research of identification technology of dynamic load distributed on the structure[J]. Journal of Vibration Engineering, 2006,19(1): 81-85.
[3] Nordström L J L, Nordberg T P. A time delay method to solve non-collocated input estimation problems[J]. Mechanical Systems and Signal Processing, 2004,18:1469-1483.
[4] Hashemi R,Kargarnovin M H.Vibration base identification of impact force using genetic algorithm[J]. International Journal of Mechanical Systems Science and Engineering, 2007,1(4): 204-210.
[5] Gunawan F E, Homma H, Morisawa Y. Impact force estimation by quadratic spline approximation[J]. Journal of Solid Mechanics and Materials Engineering, 2008, 2(8): 1092-1103.
[6] Kazemi M, Hematiyan M R, Ghavami K. An efficient method for dynamic load identification based on structural response[C]//EngOpt 2008 International Conference on Engineering Optimization,Rio de Janeiro, Brazil, 2008: 1-5.
[7] 韩旭,刘杰,李伟杰,等. 时域内多源动态载荷的一种计算反求技术[J]. 力学学报, 2009, 41(4): 595-602.
HAN Xu, LIU Jie, LI Wei-jie, et al. A computational inverse technique for reconstruction of multisource loads in time domain[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4): 595-602.
[8] 郭杏林,毛玉明,赵岩,等. 基于Markov参数精细积分法的载荷识别研究[J]. 振动与冲击, 2009, 28(3):27-30.
GUO Xing-lin, MAO Yu-ming, ZHAO Yan, et al. Load identification based on precise time-step integration for markov parameters[J]. Journal of Vibration and Shock,2009,28(3):27-30.
[9] 徐菁,张方,马小艳. 时域动载荷识别的若干修正算法[C]//第十届全国振动理论及应用学术会议论文集,南京, 2011: 796-802.
[10] 姜金辉,徐菁,张方,等. Wilson-θ反分析法的动载荷识别精度的若干问题[J]. 振动、测试与诊断, 2013,33(5):783-788.
JIANG Jin-hui, XU Jing, ZHANG Fang,et al. Accuracy of the load identification based on inverse analysis of Wilson-θmethod[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(5):783-788.
[11] 朱涛,肖守讷,阳光武. 一种新的时域动载荷识别方法[J]. 西安交通大学学报, 2012, 47(6): 968-973.
ZHU Tao, XIAO Shou-ne, YANG Guang-wu. A new time-domain method for force identification[J]. Journal of Southwest Jiaotong University, 2012, 47(6): 968-973.
[12] 王静, 陈海波,王婧. 基于精细积分的冲击载荷时域识别方法研究[J]. 振动与冲击, 2013, 32(20):81-85.
WANG Jing, CHEN Hai-bo, WANG Jing. Impulsive load identification in time domain based on precise time-integration method[J]. Journal of Vibration and Shock, 2013, 32(20):81-85.
[13] 张雄,王天舒. 计算动力学[M].北京:清华大学出版社, 2007.
[14] 蔺小林. 计算方法[M]. 西安:西安电子科技大学出版, 2009.
基金项目:航空科学基金(2012ZA52001);高等学校博士学科点专项科研基金(20123218120005);中央高校基本科研业务费专项资金(NS2012080);国家自然科学基金资助项目(51305197);机械结构力学及控制国家重点实验室自主研究课题(0115K01)
收稿日期:2014-06-30修改稿收到日期:2015-01-22
通信作者张方 男,教授,博士生导师,1962年8月生
中图分类号:TH 113; O 327
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.02.007
Numerical correcting algorithm for load identification based on quasi-static initial value
XU Jing, ZHANG Fang, JIANG Jin-hui, PU Yu-xue, JIANG Qi
(State Key Laboratory of Mechanics and Control of Mechanical Structures,College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
Abstract:A quasi-static method was presented to obtain the initial value of loading, which is a simple and quick algorithm to get stable and convergent results. The reason why the initial value of the algorithm would be not accurate was analysed, and a new load identification algorithm was deduced. The method is based on the principle of numerical algorithm and uses the idea of step-by-step correction, which can reduce the effect of cumulative error and greatly improve the stability of calculation. This numerical iteration method was applied to the load identification of a finite element model. The results of simulation and experiment show that the method can accurately identify the common variety of loads in engineering, and it has a certain ability to resist noise.
Key words:load identification; time domain; quasi-static method; numerical correction
第一作者 徐菁 女,博士生,1988年9月生

