基于动质量块和声激励共同作用下的各向同性矩形薄板动态响应分析

周志勇， 秦卫阳

(西北工业大学 力学与土木建筑学院，西安　710072)



基于动质量块和声激励共同作用下的各向同性矩形薄板动态响应分析

周志勇， 秦卫阳

(西北工业大学 力学与土木建筑学院，西安710072)

摘要：针对以往研究过程中忽略质量块惯性和声源激励对板动态响应的影响，在考虑质量块惯性对板的影响基础上，采用哈密顿原理和Kronecke δ函数建立板在动质量块和声源激励共同作用下的运动微分方程，再采用模态变换将运动微分方程进行解耦，然后采用微分求积法(DQM)求解系统动态响应。数值算例结果表明：相比Runge-Kutta算法，取样网点较少时，DQM得到的动态响应值精度更高。动质量块的质量、移动速度和阻尼系数及声激励的声频和声强对矩形薄板的动态响应曲线具有明显的影响。

关键词：动态响应；边界条件；动质量块；DQM

矩形板在动质量块和外部激励作用下的动态响应行为分析已在实际工程领域中被高度重视：在高速公路、铁路和桥梁等的设计中，众多研究人员将多数类型的桥梁近似简化为各向同性板，即将公路桥梁在外荷载作用下的振动简化为各向同性板在动质量和外部荷载激励共同作用下的振动。肖新标等[1]将列车简化成移动简谐力模型，对列车过桥时桥梁的振动形态幅频特性作了详细的探讨，给出了桥梁在不同速度下的幅频特性曲线以及TMD控制的质量比影响曲线，为进一步的桥梁振动控制提供详尽的参考数据。刘维宁等[2]以 Duhamel积分为基础，应用动力互等定理，得到了移动荷载作用下半无限弹性空间体上任意点的动力响应的一般表达式从而得到了轨道结构在移动荷载作用下动力响应的解析解形式。王少钦等[3]基于振型叠加原理， 采用广义坐标变换的方式建立了移动荷载匀变速通过简支梁桥时系统的动力平衡微分方程并以一铁路多跨简支箱梁桥为例，计算得到车辆匀速运行时桥梁最大挠度随车速的变化曲线，从车桥共振的角度详细分析了桥梁最大挠度的变化趋势以及车辆变速运行对桥梁最大挠度的影响。Wu等[4]利用有限元法(FEM)和Newmark直接积分法对承受各种动载荷的板进行受迫振动分析。Raske等[5-6]对移动荷载作用下各向同性板的动态响应进行了很好的研究，并且得到了经典的解决方案。Shadnam等[7]采用模态叠加法，简化动力学方程，基于Runge-Kutta算法实现了承受动质量块的简支矩形薄板近似解。Nikkhoo等[8]研究了四边简支矩形薄板在承载动荷载时的动力响应特性。Uzal等[9]得到了圆形薄板在动荷载作用下动态响应的解析解，但未考虑动载惯量影响。Vaseghi[10]给出了不同边界和荷载分布条件下剪切变形板振动的半解析模拟，将矩形桥面模型简化为板单元，将车辆模型近似看作动质量块。Humar等[11]基于大挠度理论和Galerkin方法，解决了车桥相互作用的问题，并确定了动态响应的相关参数。Wang等[12]研究了板自重引起的静态响应以及由动荷载耦合的动态响应。Miha等[13]研究了四边简支板在动质量块作用下的振动响应,并把质量块的荷载分布形式分别简化为集中载荷、均布载荷和线性分布载荷,研究发现质量块移动速度、荷载分布形式和质量块的质量大小对板的振动响应影响较大。Gbadeyan等[14]研究了在点声源激励下四边简支板和四边固支板的振动响应，并给出时域声压分布近似解,并对其进行了试验研究，其试验值与理论解有着较高的一致性。

基于以上分析，针对以往研究过程中忽略质量块惯性和声源激励对板动态响应的影响，本文在考虑了质量块惯性对板的影响基础上，采用哈密顿原理和Kroneckeδ函数建立了板在动质量块和声源激励共同作用下的运动微分方程；再采用模态变换将运动微分方程进行解耦，然后采用微分求积法(DQM)，求解系统动态响应。并通过不同边界条件下的算例验证了本文所提方法的可行性，着重分析了质量块质量，移动速度，边界条件，阻尼系数，声频和声强对板振动响应的影响效果。

1动质量块和声激励共同作用的各向同性矩形薄板动力学方程

均质材料的各向同性矩形薄板，x向长度为a，y向长度为b，动质量块与x轴距离为e，动质量块M在声激励作用下以速度v沿x向运动，如图1所示。

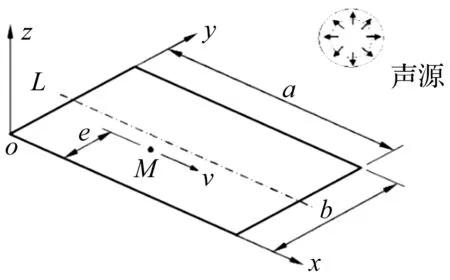
图1　动质量块和声激励共同作用下的各向同性矩形薄板Fig.1 A thin rectangular isotropic plate under moving mass and sound excitation

系统的动能：

vt)δ(y-e))dxdy

(1)

式中：M为质量块的质量；ρ，h，c分别为板的密度，厚度和阻尼系数；w(x,y,t)为板在坐标(x,y)处t时刻的挠度；用δ函数描述质量块的位置，δ函数定义如下：

(2)

板势能：

(3)

式中：μ是泊松比；D为板的弯曲刚度；

(4)

应用一般完整系哈密顿原理：

(5)

得到基于动质量块和声激励共同作用的各向同性矩形薄板运动方程：

p(x,y,t)+Mgδ(x-vt)δ(y-e)+Y

(6)

其中：

(7)

(8)

(9)

(vt,e)表示为质量块的坐标；Y表示动质量块的惯性作用。

由于本文采用单极子声源作为声激励，故p(x,y,t)可表示为坐标(x,y)处t时刻板上的声压，即考虑声源激励对矩形薄板的作用，如下式所示[15-16]：

(10)

其中：

(11)

根据以上分析，采用模态叠加法，板的挠度w(x,y,t)可表示为如下级数形式：

(12)

式中：Wmn(x,y)为对质量归一化的第(m,n)阶振型函数，Tmn(t)为相应的模态坐标函数。

将式(12)代入式(6)，并在方程两端同时乘Wηε(x,y)，再对x从零到a积分，对y从零到b积分，假设阻尼在模态变换中可对角化并令2ωηεζηε=c，可得：

(13)

若η为1…nq，ε为1…mq，则方程(13)可写成矩阵形式：

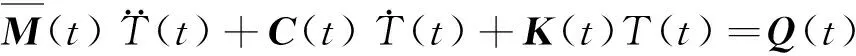
(14)

(15)

(16)

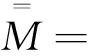
(17)

C(t)=Cd+Cu

(18)

其中：

Cd=2Diag[ζ11ω11…ζ1nqωmnζ21ω21…

ζ2nω2nqζmq1ωmq1…ζmqnqωmqnq]

(19)

Cu=

(20)

K(t)=Kd+Ku

(21)

Kd=

(22)

Ku=

(23)

Q(t)=[W11…W1nqW21…

W2nqWmq1…Wmqnq]T×

(24)

(25)

2不同边界条件下板振型求解方法

根据上述动力学方程的分析可知，求解矩形薄板的动力学方程时，需要求解板的各阶振型函数，即求解式(12)。本文以四边简支矩形薄板和对边简支对边自由的矩形薄板作为例，给出了相应的各阶振型函数求解方法：

(1) 四边简支板(SSSS)

四边简支板的振型边界条件[17]：

(27)

(28)

满足式(27)和(28)的振型解可直接用双三角函数来表示：

(29)

相应的第(m,n)阶固有频率ωmn可表示为：

(30)

其中：

(31)

(2) 对边简支对边自由板(SSFF)

平行于x轴两边为自由边界情况下，振型边界条件为[17]：

(32)

(33)

相应的第(m,n)阶固有频率ωmn可由下式得到：

(34)

相应的振型函数为：

(35)

其中：

αmn=

β1m,β2m为满足振动微分方程的特征方程的特征根：

(37)

(38)

平行于x轴两边为自由边界情况下，振型边界条件为[17]：

(39)

(40)

相应的第(m,n)阶固有频率ωmn可由下式得到：

2β1mβ2m(cosβ1mbchβ2mb-1)=0

(41)

相应的振型函数为：

Wmn(x,y)=[(β2mnsinβ1mny-β1mnshβ2mny)+

(42)

其中：

(43)

(4) 四边固支板(CCCC)

对于四边固支板可采用梁函数法，振型解可表示为[18]：

Wmn(x,y)=Xm(x)Yn(y)

(44)

式中：

Xm(x)=A1msinαmx+A2mcosαmx+

A3mshαmx+A4mchαmx

(45)

Yn(y)=B1nsinβny+B2ncosβny+

B3nshβny+B4nchβny

(46)

相应的第(m,n)阶固有频率ωmn可由下式得到:

(47)

其中：

A1m=-A3m=1,

(48)

(49)

其中参数αm,βn可由固支梁弯曲振动特征方程得到：

cosλchλ-1=0

(50)

其中：

λ=aαm或bβn

(51)

3微分求积算法(DQM)

设f(ti)为一任意微分方程的解，选取非均匀网点m个，网点坐标为：

(52)

其中tT所求的时间区间长度。

(53)

(54)

其中:Aij和Bij分别为一阶导数加权系数和二阶导数加权系数。

可利用Lagrange插值函数得到一阶导数加权系数：

其中：

(56)

二阶导数加权系数为：

4微分求积(DQM)近似解

采用DQM法解方程(14)，本文选取非均匀网点N个，网点坐标为：

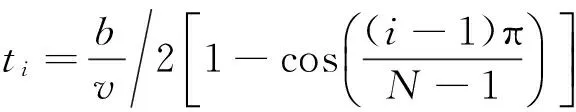
i=1,2,…,N

(58)

其中:b/v是时间跨度，模态坐标函数Tmn(t)的一阶导数，二阶导数为：

l=1,2,…,nq

(59)

在任意网点处的模态坐标函数为：

[K(ti)]{T(ti)}={Q(ti)},

i=1,2,…,N

(60)

其中：

(61)

(62)

方程(61)和(62)的级数形式可分别写为：

(63)

(64)

将式(63)和(64)代入式(60)可得：

[K(ti)]{T(ti)}={Q(ti)},

i=1,2,…,N

(65)

根据以上分析，式(65)可写为如下形式：

(66)

其中：

式(66)可简化如下：

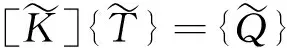
(68)

5微分求积(DQM)初始条件及方程组求解

给出式(68)的初始条件为：

{T(ti)}={T(0)}={T0}

(69)

(70)

根据式(69), 式(70)可写为：

(71)

将方程(69)和(71)代入方程(68)可得：

(72)

(73)

(74)

(75)

根据以上公式，即可求得式(73)中的动态响应值。

6数值算例与分析

算例1采用本文所提方法计算四边简支各向同性板在8.894 N的移动荷载下的DMF(Dynamic Magnification Factor)指数，DMF表示矩形薄板的最大中心动力挠度与最大中心静力挠度之比，然后与已有参考文献[15-16,18]的结果做了对比。临界速度为SP=vcr=1表示移动荷载以板为一阶频率自振周期的时间通过板的速度。板的参数如下：板长宽a=b=0.101 6 m，板厚h=0.002 54 m，e=b/2，弹性模量E=2.068 4e11 Pa，密度ρ=10 695.790 2 kg/m3，泊松比μ=0.3，选取非均匀网点个数N=40。

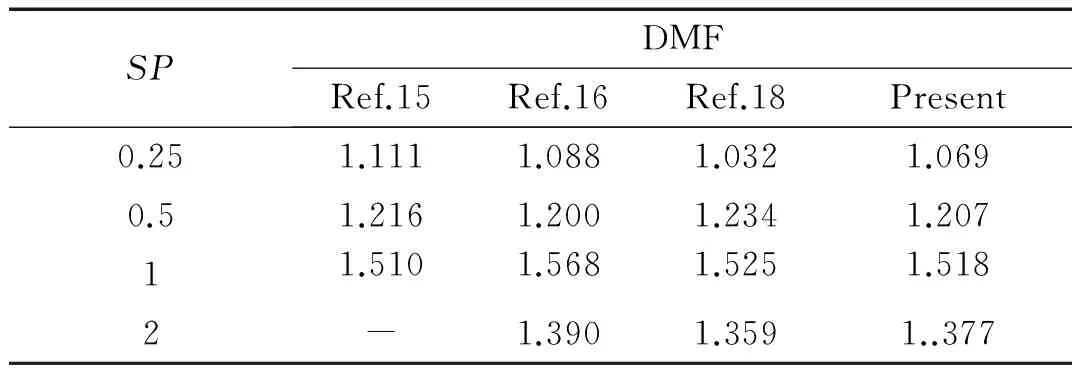
表1　在移动荷载作用下板的DMF

算例2设板的参数如下：板的长度a=24 m，宽度b=8 m，板厚h=1 m，弹性模量E=50 GPa，密度ρ=2 400 kg/m3，泊松比μ=0.3，动质量块系数λ=M/ρabh，声频率用sf表示，临界速度vcr=af，其中f为

板的一阶频率。

图2～图11均为对边简支对边自由(SSFF)板。图2给出基于DQM算法与Runge-Kutta算法得到的动态响应曲线对比图。Wdc为移动质量块引起的板中心挠度，Wsc为相对应静力荷载作用在板中心时引起的板中心挠度。为了能够清楚地反映质量块经过板时，给予板的振动能量。当vt/a(质量块位置/板跨度)小于1时表示质量块未离开板，当vt/a大于1时表示质量块滑出了板的边界，此时对应于板的自由振动，主要是为了分析一个板的振动全过程。从图中可以看出，当取样点数较多，如N=40时，DQM算法与Runge-Kutta算法均可取得较好的精度；当取样点数降低时，相比Runge-Kutta算法，基于DQM算法求解得到的动态响应值精度较高，亦采用DQM算法可大大减少计算量，原因在于Runge-Kutta算法采用均匀取样点，DQM算法则采用非均匀取样点。鉴于此，为减少计算代价，应优先考虑DQM算法。

图2 不同求解方法下板的中心挠度随质量块位置变化图(λ=0.01,ξ=0,Q=0,e=4,v=vcr)Fig.2Thedeflectionoftheplatefordifferentsolvingmethodsundermovingmass图3 在不同声压作用下板的中心挠度随质量块位置变化图(λ=0.01,ξ=0,e=4,v=vcr)Fig.3Thecentredeflectionofplatewithdifferentsoundpressureversusmassposition图4 不同移动速度下板的中心挠度随质量块位置变化图(λ=0.01,ξ=0,Q=0,e=4)Fig.4Thecentredeflectionofplatefordifferentmovingspeedsversusmassposition

图5 板在质量块和移动荷载作用下板的中心挠度随质量块位置变化曲线(ξ=0,Q=0,e=4,v=vcr)Fig.5Thecentredeflectionofplatefordifferentmassparametersversusmasspositionundermovingmassormovingload图6 板在质量块和移动荷载速度不同时板中心挠度随质量块位置变化曲线(λ=0.01,ξ=0,Q=0,e=4)Fig.6Thecentredeflectionofplatefordifferentmovingspeedsversusmasspositionundermovingmassormovingload图7 板的DMF在不同质量块作用下随速度变化曲线(ξ=0,Q=0,e=4)Fig.7TheDMFofplatefordifferentmassparametersversusmovingspeed

图3给出不同声压时，矩形薄板的动态响应值随质量块的位置变化曲线。从图中可以看出，质量块位置一定时，随着声压的增大，板的动态响应曲线不断上移，即板的挠度不断增大。

图4表示质量块在不同移动速度时，矩形薄板的动态响应值随质量块位置变化曲线。从图中可以看出, 质量块位置一定时，随着速度的不断增加，动态响应曲线幅值变化明显，且最大响应值不断增大，曲线亦越平滑。

图5给出矩形薄板在质量块和移动荷载作用下，动态响应值随质量块位置变化曲线。从图中可以看出，相比移动荷载而言，由于板的动态响应受动质量块惯性的影响，板的动态响应峰值增加，可见动质量块的惯性是影响曲线变化的因素之一，随着动质量块系数的不断增大，曲线的峰值的绝对值不断上移，即峰值不断增加。

图6给出矩形薄板在质量块和移动荷载速度不同时，动态响应值随质量块位置变化曲线。从图中可以看出，随着质量块移动速度的增加，板的中心挠度曲线变的越来越平滑，随着速度的增加，板动态响应幅值越来越大。质量越大，质量块的惯性作用对板的影响越大。当动质量块移动速度较大时，曲线的峰值亦较大。

图7给出矩形薄板在不同质量块作用时，DMF值随速度变化曲线。从图中可以看出，随着质量块移动速度的增加，板的DMF值越来越大，当速度达到一定值时，DMF值达到最大，即DMF出现峰值，继而随着速度再次增大时，DMF从峰值开始下降。 随着动质量块系数λ的增大，DMF曲线不断上移，表明随质量块质量的增加质量块惯性对板的DMF影响越大。

图8给出矩形薄板在不同阻尼作用时，DMF值随速度变化曲线。从图中可以看出，随着速度的增加，板的DMF值越来越大，当速度达到一定值时，DMF值达到最大，即DMF出现峰值，继而随着速度再次增大时，DMF从峰值开始下降。因为阻尼力的方向总是与板运动的方向相反，所以随着阻尼比系数ξ的增大，DMF曲线不断下移，表明质量块的阻尼比系数对板的DMF影响越大。

图9给出矩形薄板在不同声压幅值作用时，DMF值随质量块位置变化曲线。从图中可以看出，当质量块位置的不断增加，但小于0.5时，DMF值曲线会出现不规则趋势，这是由于质量块低速运动时，通过板的时间较长，受声源影响时间较长，受声压影响较大，导致和动质量块共同作用在板上时使板的动态响应DMF曲线发生不规则变化，当动质量块移动速度不断增大时，声激励作为外部激励与质量块共同作用的时间较短，作用在板上得到的动态响应DMF曲线则会出现规则变化。另外声源激励对质量块移动产生了一定的影响，这在后续工作是研究的热点，后续工作可考虑外部激励与动质量块的协同耦合相关作用。随着声压幅值Q的增大，DMF曲线不断上移，表明声压幅值Q对板的DMF影响越大，出现这种情况的原因在于声压大，在板上的压力就越大，进而增加了板的挠度。

图10给出矩形薄板在不同声压频率作用时，DMF值随质量块移动速度变化曲线。从图中可以看出，在速度小于0.5倍的临界速度时，当声压的频率等于板的一阶自振频率时，声压与板产生共振作用，声压对板的DMF影响显著，当质量块速度大于0.6倍的临界速度时，由于速度增大质量块在板上运动的时间减少，共振对板的影响时间变短，所以对板的DMF影响相对减小。当速度增加，声压频率越小板DMF影响越大。以上分析表明考虑动质量块和声激励共同作用具有重要的研究意义。

图8 不同阻尼作用下板的DMF随速度变化曲线(λ=0.01,Q=0,e=4)Fig.8TheDMFofplatefordifferentdampingparametersversusmovingspeed图9 不同声压幅值作用下板的DMF随质量块速度变化曲线(λ=0.01,Q=0,e=4,sf=0.5f)Fig.9TheDMFofplatefordifferentsoundpressureversusmovingspeed图10 不同声压频率作用下板的DMF随速度变化曲线(λ=0.01,ξ=0,Q=1000,e=4)Fig.10TheDMFofplatefordifferentsoundexcitingfrequencyversusmovingspeed

图11 不同阻尼作用下板的最大中心加速度随速度变化曲线(λ=0.01,Q=0,e=4)Fig.11Themaximumcenteraccelerationofplatefordifferentdampingparametersversusmovingspeed图12 不同边界条件板的DMF随移动速度(vcr为相应边界条件极限速度)变化曲线(λ=0.01,Q=0,e=4)Fig.12TheDMFofplatewithdifferentboundaryplatesvarieswithspeed(vcrisrelativecriticalspeed)图13 不同边界条件板的DMF随移动速度(vcr(CCCC)为四边固支板极限速度)变化曲线(λ=0.01,Q=0,e=4)Fig.13TheDMFofplatewithdifferentboundaryplatesvarieswithspeed(vcr(CCCC)isthecriticalspeedofallclampedplate)

图11给出不同阻尼作用下，矩形薄板的最大中心加速度随速度变化曲线。从图中可以看出动质量块速度在0.7和0.9的临界速度时，阻尼对板的DMF影响显著, 板的振动幅值受到外界激励力的频率影响和阻尼率的影响较大，出现该现象的原因在于阻尼力的方向与板运动方向相反，故阻尼越大，在到达某一速度时，矩形薄板的最大中心加速度受到阻尼率的影响极为显著，故在那一速度时，板的最大加速度有显著的变化。当超越那一临界速度时阻尼率的影响又逐渐变弱。

7结论

本文针对不同边界条件下各向同性矩形薄板振动研究过程中忽略质量块惯性和声源激励对板的相互作用，提出了基于动质量块和声激励共同作用的各向同性矩形薄板动态响应分析。该方法采用Kroneckeδ函数描述动质量块的位置及其与板的相互作用，同时考虑单极子声源作为外部激励，建立了动质量块和声激励协同作用的运动微分方程。基于微分求积法，求解动态响应值，并通过不同边界条件下的算例验证了本文所提方法的可行性，得到如下结论：

(1) 相比Runge-Kutta算法，取样较少时，DQM算法计算量小，可以用权重系数表示高阶导数，得到的动态响应值DMF精度更高，且数学原理简单，可操作性强，易于在计算机上实施，精度较高，是一种有效的数值计算方法。

(2) 采用微分求积法计算板在移动荷载用下板的DMF，并与现有文献进行了对比，用于保证计算结果的准确性。

(3) 当同时考虑动质量块和声源激励对矩形薄板的作用时，质量块速度，板的阻尼，声压幅值，声压频率，质量块质量均对矩形薄板动态响应DMF值有着非常明显的影响。

(4) 当同一质量块通过不同边界条件的板时，对于自振频率较小的板，其相对应的临界速度亦较小，其实际挠度值较大。反之，对于自振频率较大的板，其相对应的临界速度亦较大，其实际挠度值较小。

参 考 文 献

[1] 肖新标, 沈火明. 移动荷载作用下的桥梁振动及其TMD控制[J]. 振动与冲击,2005, 24(2): 58-62.

XIAO Xin-biao, SHEN Huo-ming. Vibration and the TMD control of bridges under moving loads[J]. Journal of Vibration and Shock, 2005, 24(2): 58-62.

[2] 刘维宁，张昀青. 轨道结构在移动荷载作用下的周期解析解[J]. 工程力学, 2004, 21(5):100-103.

LIU Wei-ning, ZHANG Yun-qing. A periodic analytical solution of railway track structure under moving loads[J]. Engineering Mechanics, 2004, 21(5):100-103.

[3] 王少钦, 夏禾, 郭薇薇, 等. 变速移动荷载作用下简支梁桥的动力响应及共振分析[J]. 振动与冲击,2010,29(2): 26-32.

WANG Shao-qin, XIA He, GUO Wei-wei, et al. Dynamic response and resonance analyses for a simply-supported bridge under speed-varying loads[J]. Journal of Vibration and Shock, 2010, 29(2): 26-32.

[4] Wu J S, Lee M L, Lai T S. The dynamic analysis of a flat plate under a moving load by the finite element method [J]. International Journal for Numerical Methods in Engineering, 1996, 193(1): 307-314.

[5] Raske T F, Schlack A L. Dynamic response of plates due to moving loads [J]. Journal of the Acoustical Society of America, 1967, 42(3):625-635.

[6] Fryba L. Vibration of Solids and Structures under Moving Loads[M]. London: Thomas Telford Publishing,1972.

[7] Shadnam M R, Mofid M, Akin J E. On the dynamic response of rectangular plate with moving mass [J]. Thin-Walled Structures, 2001, 39(9):797-806.

[8] Nikkhoo A, Rofooei F R. Parametric study of the dynamic response of thin rectangular plates traversed by a moving mass [J]. Acta Mechanica, 2012, 223(1): 15-27.

[9] Uzal E, Sakman, L E. Dynamic response of a circular plate to a moving load [J]. Acta Mechanica, 2010, 210 (3/4):351-359.

[10] Vaseghi A J, Mehri B. A new orthonormal polynomial series expansion method in vibration analysis of thin beams with non-uniform thickness [J]. Applied Mathematical Modelling, 2013, 37(18/19):8543-8556.

[11] Humar J L, Kashif A H. Dynamic response analysis of slab-type bridges[J].Journal of Structural Engineering, 1995, 121(1): 48-62.

[12] Wang R T, Kuo N Y. Nonlinear vibration of Mindlin plate subjected to moving forces including the effect of weight of the plate[J]. Structural Engineering and Mechanics,1999,8(2): 151-164.

[13] Miha P, Gregor C, Miha B. Structural-acoustic model of a rectangular plate-cavity system with an attached distributed mass and internal sound source: Theory and experiment [J]. Journal of Sound and Vibration, 2014, 333(7): 2003-2018.

[14] Gbadeyan J A, Dada M S. A comparison of dynamic responses of three versions of moving load problem involving elastic rectangular plates [J]. Journal of Vibration and Control, 2010, 17(6): 903-915.

[15] Kinsler L E. Fundamentals of Acoustics[M].New York: Wiley,1982.

[16] Reynolds D D. Engineering Principles of Acoustics, Noise and Vibration Control [M]. Boston: Allyn and Bacon Inc.

[17] 曹志远. 板壳振动理论[M].北京：中国铁道出版社,1986.

[18] Au F T K, Wang M F. Sound radiation from forced vibration of rectangular orthotropic plates under moving loads [J]. Journal of Sound and Vibration, 2005, 281(3/4/5): 1057-1075.

基金项目：国家自然科学基金 (11172234) 资助

收稿日期：2014-09-12修改稿收到日期：2015-01-07

通信作者秦卫阳 男，教授,博士生导师，1967年4月生

中图分类号:O321

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.022

Dynamic responses of thin rectangular isotropic plates under actions of moving mass and acoustic excitation

ZHOU Zhi-yong, QIN Wei-yang

(School of Mechanics, Civil & Architecture, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:Aiming at that in the past studies the effects of mass inertia and sound source excitation on dynamic responses of a plate were ignored, here the differential equations of motion for a plate under action of moving mass and sound source excitation were established using Hamilton’s principle and kronecke δ function. The differential equations of motion were decoupled using the modal transformation, then they were solved with the differential quadrature method (DQM). The numerical results showed that DQM has a higher accuracy for the dynamic responses of the plate than Runge-Kutta algorithm does when the number of grid points is small; the moving mass, moving speed, damping, and acoustic excitation frequency and intensity have significant impacts on the dynamic responses of the plate.

Key words:dynamic response; boundary conditions; moving mass; DQM

第一作者 周志勇 男，博士生，1986年9月生