基于EEMD的混合陶瓷球轴承故障双冲击特征提取

孔佑炳， 郭　瑜, 伍　星

(昆明理工大学 机电工程学院，昆明　650500)



基于EEMD的混合陶瓷球轴承故障双冲击特征提取

孔佑炳， 郭瑜, 伍星

(昆明理工大学 机电工程学院，昆明650500)

摘要：疲劳剥落是导致滚动轴承失效的主要原因，当滚道出现剥落故障时滚动体在进入和退出剥落区时的加速度振动信号表现出不同特征：进入故障区时产生以较低频率成分为主的阶跃响应；退出剥落区则引起频带较宽的脉冲响应。有效分离这两类信号特征，对实现对混合陶瓷球轴承剥落区长度的测量有重要意义。提出一种基于总体经验模态分解(EEMD)的混合陶瓷球轴承剥落故障双冲击特征提取方法，该方法首先用AR模型对原始振动信号进行预白化处理，然后利用EEMD对白化后的振动信号进行去噪，并结合Hilbert包络提取算法实现对剥落故障混合陶瓷球轴承振动信号双冲击特征的有效分离提取。仿真及试验研究表明该方法能够有效地分离出混合陶瓷球轴承故障双冲击特征。

关键词：包络分析；EEMD；混合陶瓷球轴承；双冲击；轴承故障

近年来，混合陶瓷球轴承[1](内外圈为金属，滚动体为氮化硅(Si3N4)等陶瓷材料)在高端机床电主轴上得以广泛应用，但目前针对混合陶瓷球轴承故障检测和评价方法极其有限[1]，周井玲等[2]指出混合陶瓷球轴承最常用的氮化硅(Si3N4)陶瓷球的主要失效形式也是疲劳剥落，开展相关研究有重要意义。另一方面，剥落区长度是表征故障程度的重要特征量之一，通过对滚动轴承剥落区长度测量实现对混合陶瓷球轴承故障程度的评价有重要研究价值，但对剥落故障区长度的测量，通常需要将轴承拆下进行，显然并不适合在运行工况下进行。Randall等[3-4]提出了一种基于球轴承疲劳剥落故障引起振动信号的双冲击特征进行剥落区长度估计的方法，即提取振动信号中对应进入和退出剥落故障区的两个时间点，实现对剥落区长度的估算。该方法通过对故障振动信号双冲击特征的提取，为实现在运行工况下剥落区长度的测量提供了一种较为可取的方法。但值得指出的是对混合陶瓷球轴承振动信号故障特征提取的研究还鲜有报道。

本论文研究中通过QPZZ-Ⅱ旋转机械振动故障模拟试验台对已知的外圈故障尺寸的混合陶瓷球轴承进行了大量试验，研究发现有剥落故障的混合陶瓷球轴承故障振动信号同样存在双冲击现象，且与金属球轴承疲劳剥落故障振动信号特征类似，其在剥落区进入时具有阶跃响应特征，退出时具有脉冲响应特征。但由于旋转机械工况条件下其振动为多源混合信号，在原始振动信号中通常不易直接观察到双冲击现象。为了有效地分离出混合陶瓷球轴承剥落故障引起振动的双冲击特征，本文提出了一种基于总体经验模态分解(EEMD)的混合陶瓷球轴承故障双冲击特征提取方法，即先对原始振动信号进行预白化处理，再利用EEMD对白化后的信号进行降噪处理，并结合Hilbert包络提取方法实现对剥落故障混合陶瓷球轴承振动信号双冲击特征的分离提取，为故障程度评价奠定了基础。

1故障轴承双冲击现象

1.1双冲击特征研究简介

Epps[5]最先论述了滚动轴承故障的双冲击现象，并以外圈滚道点蚀剥落为例，指出发生剥落故障的滚动轴承，其滚动体进入剥落区前边缘和撞击剥落区后边缘时，相应的振动信号表现出不同的特征：进入剥落区前边缘时(进入点)振动信号呈现出阶跃响应特性，以相对较低(与退出时引起的冲击相比)的频率成分为主；撞击剥落区后边缘时(退出点)振动信号则呈现出频带较宽脉冲响应特性，且进入点、退出点的时间间隔随着故障尺寸的增加而增加。Dowling[6]指出了退出点相对于进入点有180°相位突变，且这两个事件均为脉冲响应，其认为两个脉冲峰值间隔和故障尺寸相对应，但其并未给出相关理论说明。Randall等[3-4]研究了外圈滚道剥落故障振动信号双冲击特征分离提取，其结果与Epps所提观点更为相似，而非Dowling所提出的两个事件均为脉冲响应。

图1　外圈剥落故障引起双冲击现象示意Fig.1 Double impulses phenomenon illustration caused by peeling off the bearing outer ring

图1为双冲击现象示意，如图1(a)所示，阶跃响应特征是由于滚动体中心旋转位于剥落区前缘正上方时，滚动体回转中心变为A点，同时受力减小(非瞬间减小[3])而产生；脉冲冲击响应特征的发生是由于滚动体撞击剥落区后缘产生(图1(b)可看出，此时滚动体中心刚好滚过剥落区的一半距离)，滚动体回转中心由A点变到B点，同时其回转方向也在此刻发生变化，在一个完整剥落区运动过程中，滚动体从进入剥落区前缘时受力减小到撞击后缘时的重新受力，会产生一个更剧烈的冲击，进而可知进入退出两个事件具有不同的响应特征。但应指出的是，在机械工作过程中，采集到的振动信号有多个振源组成，且受背景噪声等多重因素的影响，使得采集到的原始振动信号较为复杂，通常需要对原始振动信号采用适合的信号处理方法处理后才能对双冲击现象进行有效分离。

1.2混合陶瓷球轴承双冲击特征

本文通过对故障尺寸分别为0.5 mm，1.0 mm，2.0 mm的单一混合陶瓷球轴承外圈故障(图2)在不同转速下运转过程中的振动信号进行采集分析研究，得到双冲击特征结果如图3所示(以转速为586 r/min为例)，可以明显看出进入退出具有不同信号特征，且其冲击时间间隔随着故障尺寸增加而增加。

图2　故障尺寸分别为0.5 mm,1.0 mm,2.0 mm混合陶瓷球轴承外圈Fig.2 Hybrid ceramic ball bearing outer race with the fault sizes (0.5 mm,1.0 mm, 2.0 mm)

图3　转速为586 r/min下的双冲击信号特征Fig.3 Double impulses characteristic waveform under 586 r/min

2基于EEMD的双冲击特征分离提取

2.1EEMD算法简介

经验模态分解(EMD)方法可将复杂信号自适应地分解成一系列本征模态函数(Intrinsic Mode Function，IMF)之和，通过将某些IMF进行重新组合可实现信号的降噪，其原理详见文献[7]。其分解结果依赖于信号本身，较适用于非线性非平稳过程分析，目前在机械故障诊断领域得以广泛应用[8]。但若被分析信号中存在间断信号，脉冲干扰和噪声等干扰，会使EMD产生模态混叠，为此Wu等[9]提出一种集合经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)方法，可有效抑制模态混叠现象。EEMD的本质是一种叠加高斯白噪声的多次EMD，利用了高斯白噪声具有频率均匀分布的统计特性，使加入噪声后的信号在不同尺度上具有连续性，有效地解决了由间歇性成分导致的模态混叠问题。文献[10]对EEMD降噪原理进行了详述，并指出EMD执行次数取100～300时，加入白噪声的强度选择0.01～0.5倍待分析信号的标准偏差较为适宜，且两个参数均可随噪声的强度而适当增大。

2.2包络提取方法简介

虽然近年来提出了基于复频移Morlet小波变换的包络提取、基于谱峭度的复包络提取[11]等包络提取算法，因论文主题非包络提取技术，论文研究中仍使用目前广泛使用的基于Hilbert变换的包络提取，但其他包络提取应同样适用。基于Hilbert变换的包络提取法以信号本身作为实部，以信号的Hilbert变换作为虚部构建解析信号。其解析信号的幅值即为信号的包络。

2.3基于EEMD的双冲击特征分离提取方法

由于滚动球轴承故障引起的振动信号易被噪声干扰所淹没，从原始振动信号中不易直接观察到双冲击特征。Randall等[3]研究了基于Morlet小波降噪的故障滚动轴承双冲击特征的包络提取方法，但Morlet小波存在需要根据信号选取适合中心频率及带宽等问题。EEMD分解可以弥补小波降噪方法对调频调幅信号处理过程中存在的特征波匹配缺陷[9]，同时还能有效抑制EMD分解所存在的模态混叠现象。因此，为准确分离出双冲击特征，本文提出了一种基于EEMD的自适应降噪的混合陶瓷球轴承双冲击特征包络提取分离方法，其基本步骤包括：

步骤1预白化处理。自回归(AR)模型可用于去除信号中的确定成分[4]，而峭度对冲击十分敏感。因此，以峭度值最大时所对应的AR模型阶次对信号进行滤波，不仅可以去除信号中的确定成分，还可使残余信号中故障对应的冲击较为明显。预白化处理步骤如下：首先确定AR 的阶次范围(本文取400以内)，并计算各阶次下的峭度值K[12]：

(1)

式中：xi为振动信号，x为信号均值，N为信号采样长度，σ为信号标准差。找出最大峭度值，并以其对应的阶次作为AR模型最优阶次对信号按下式所示AR模型[12]进行线性预测。

(2)

式中:p为AR模型的阶次，ak(k=1,2,…,p)为自回归加权参数，ηi为AR模型残余信号，主要包含噪声及信号中非平稳信号，即故障轴承冲击的主要成分。

步骤2基于EEMD的降噪处理。对步骤1中所得残余信号进行EEMD分解得到一组从高频到低频的本征模态函数(IMF)。首先自动筛选IMF重构的方法去除含噪比例较大的IMF分量[10]，再对剩余的IMF进行重构，并计算各IMF分量与重构后信号的互相关系数及其峭度值，最后选取互相关系数及峭度值较大的IMF进行重构[13]，得到去噪后信号。具体步骤如下：

① 按下式计算各IMF分量的能量密度与其平均周期的积[10]：

(3)

式中：N为各IMF的长度，Aj为第j个IMF分量的振幅，Kj为第j个IMF的极值点总数。再计算系数RPj(j≥2)[10]：

(4)

当RPj≥ 1时，则将前面的j-1个IMF分量作为噪声去除，同时将所有剩余IMF分量进行重构；

② 计算各IMF分量与步骤①中重构信号的互相关系数及各IMF分量的峭度值，然后选取相关系数及峭度值均较大的IMF分量进行重构，得到降噪信号。

步骤3包络提取双冲击特征。对去噪后的信号进行基于Hilbert变换实现双冲击特征的有效提取。

3仿真和试验

3.1仿真研究

仿真一转速为586 r/min的混合陶瓷球轴承匀速运转过程多振源信号，其阶跃响应sδ(t)表示为[2]：

sδ(t)=Aδe(-t/3τ)sin(2πfrt)

(5)

脉冲响应冲击数学模型sε(t)表示为[2]：

sε(t)=-Aεe(-t/5τ)cos(2πtfr/1.8)+e(-t/8τ)

(6)

式中：Aδ、Aε分别为阶跃响应、脉冲响应信号幅值，τ为阻尼系数，fr为轴承固有频率。研究中取fr= 10 500 Hz，τ=0.000 1，Aδ=1，Aε=1。并按两个阶跃响应、脉冲响应之间存在小于2%的随机滑移分别生成阶跃、脉冲响应系列，并分别按以下两式分别进行调制处理：

sδ_fa(t)=a(0.02+bsδ)cos(2πfzt+βsδ)

sε_fa(t)=a1(0.02+b1sε)cos(2πfzt)e(-t/5τ)+

e(-t/0.5τ)

(7)

式中：a为调幅信号幅值，b为调制指数，fz为载波频率，研究中取a=1，b=1，β=50，fz= 105 000 Hz。得到调制后阶跃响应如图4(a)，调制脉冲响应如图4(b)。调制后脉冲响应系列延迟35个采样点后加到阶跃响应系列，作为轴承的双冲击特征信号如图4(c)所示，仿真中再加与双冲击特征信号信噪比为30 dB的粉红色噪声及另外两个其他结构共振信号:

(8)

式中:取幅值Aδ1=5、Aδ1=1.6；固有频率fr1= 1 800 Hz，fr2= 6 400 Hz。对其进行归一化处理后得到波形如图4(d)所示，与图4(e)为实验采集所得原始振动信号归一化处理波形比较，两者基本一致。

图4　仿真双冲击信号Fig.4 Simulated waveform of double impulses

IMF系列号123456RP系数0.90611.51231.85392.616711.49525.2365

表2　剩余各IMF分量与重构信号互相关系数及其峭度值

按2.3节所述方法对仿真信号如图5(a)所示，经AR处理后得到残余信号波形如图5(b)所示，图5(c)，5(d)分别为图5(a)，5(b)的局部放大图。从图5(d)中可以看出，原始振动信号经AR预白化处理后，双冲击现象明显增强，然后对白化残余信号利用EEMD进行分解得到各IMF如图6所示(分解得到13个IMF，选取了前6个IMF进行显示)，分解过程中高斯白噪声标准差为0.016 8，分解次数为180次。再按2.3所述重构方法，计算出各IMF分量的RP系数如表1所示。

图5　仿真振动信号Fig.5 Simulated vibration signal

图6　仿真信号EEMD分解结果Fig.6 Ensemble empirical mode decomposition (EEMD) results of simulation signal

由表1知第二个IMF的RP系数为1.512 3>1，因此，第一个IMF应作为噪声去除直接去除，再将剩余各IMF进行重构并计算剩余各IMF分量与重构后信号的互相关系数及峭度值如表2所示，取互相关系数及峭度值均较大的IMF2、IMF3、IMF4、IMF5进行重构得到最终降噪信号如图7(a)所示波形，对重构信号进行希尔伯特包络提取后所得波形如图7(b)所示，图7(c),7(d)分别为图7(a),7(b)的局部放大波形，从图7(d)所示波形可以清晰看出双冲击特征，及其所对应的冲击间隔，和仿真延时35采样点几乎一致。

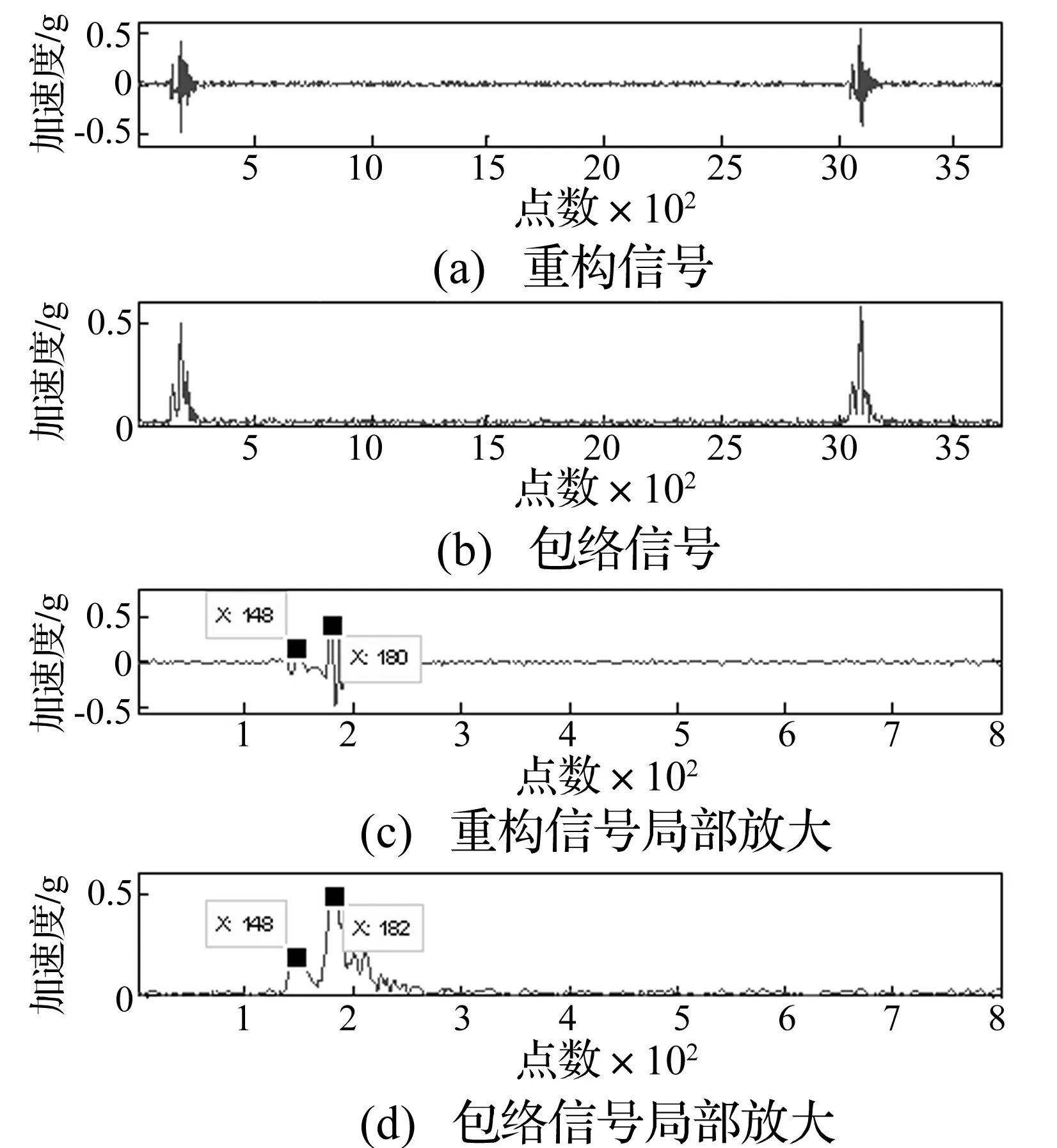
图7　Hilbert包络信号Fig.7 Enveloped signals based on Hilbert

3.2测试试验分析

研究中以旋转机械振动及故障模拟实验台QPZZ-Ⅱ系统(图8)为测试对象进行了实际试验研究。在轴承座内安装一存在外圈单一故障的混合陶瓷球轴承。

图8　QPZZ-Ⅱ试验台Fig.8 QPZZ-Ⅱ test rig

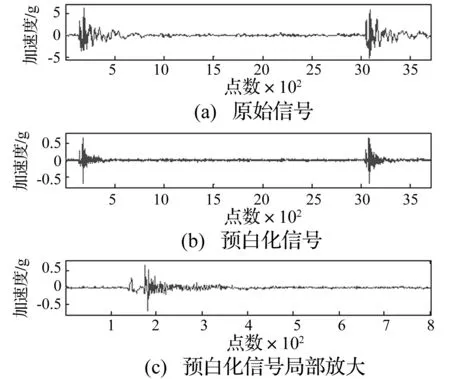
图9　实测信号Fig.9 Measured vibration signal

本文所用试验参数如下：轴承型号为6205，其内径为25 mm，外径为52 mm，滚动体为氮化硅(Si3N4)陶瓷球，直径为7.938 mm，滚动体数目为9，接触角为0°；外圈故障尺寸：0.5 mm；轴转速586 r/min，数据采集设备为NI USB9215采集卡，采样频率为102.4 kHz。采集获得的原始振动信号波形如图9(a)所示。采用本文所提出方法，先对原始测试振动信号进行白化处理得到的残余信号如图9(b)所示，对其进行局部放大后可以看到阶跃响应及脉冲响应特征得到明显增强如图9(c)所示。对残余信号进行EEMD分解得到IMF分量，如图10所示(分解得到13个IMF，显示了前6个IMF)，分解过程中高斯白噪声标准差为0.089 8，分解次数为180次。按2.3所述重构方法，计算出各IMF分量的RP系数如表3所示(EEMD分解得到13各IMF，表里只显示了其前6个)。

表3　各IMF分量RP系数

图10　实测信号EEMD分解结果Fig.10 Ensemble empirical mode decomposition (EEMD) results of the measured signal

由表3知第二个IMF的RP系数为1.143 6>1，则第一个IMF分量应作为噪声直接去除，然后将剩余各IMF进行重构，并计算剩余各IMF分量与重构后信号的互相关系数及峭度值如表4所示，取互相关系数及峭度值均较大的IMF2、IMF3、IMF4、IMF5进行重构得到降噪信号如图11(a)所示，对重构信号进行希尔伯特包络提取后所得波形如图11(b)所示，图11(c),11(d)分别为图11(a),11(b)的局部放大波形。由图11(d)中可以看出，经过EEMD降噪并进行包络处理后可以清晰的看出滚子进入和退出故障区时的双冲击特征，从而实现了混合陶瓷球轴承双冲击分离及冲击时间间隔的提取。其双冲击时间间隔与剥落区长度的对应关系及其剩余使用寿命预测方法将在下一步的研究工作中开展。

表4　剩余各IMF分量与重构信号互相关系数及其峭度值

图11　Hilbert包络信号Fig.11 Enveloped signals based on Hilbert

4结论

外圈剥落故障混合陶瓷球轴承运转过程中，滚子进入和退出剥落区时，其加速度振动信号同样存在双冲击现象。本文所提基于EEMD的剥落故障混合陶瓷球轴承的双冲击特征提取方法，能够在机械运转过程中受多振源、强背景噪音及信号传输路径等诸多因素的影响下，实现混合陶瓷球轴承双冲击特征的包络提取，对实现其剥落区长度在运转条件下的预测具有潜在研究价值，仿真和实验证明了本方法的有效性。

参 考 文 献

[1] Dempsey P J, Certo J M, Morales W. Current status of hybrid bearing damage detection[R]. NASA/TM—2004-212882, NASA, Cleveland, OH, 2004.

[2] 周井玲, 吴国庆, 陈晓阳. 氮化硅陶瓷球滚动接触疲劳寿命模型[J].机械工程学报，2008, 44(2):37-42.

ZHOU Jing-ling, WU Guo-qing, CHEN Xiao-yang. Tensile stress life model for rolling contact fatigue of silicon nitride ceramic balls [J]. Journal of Mechanical Engineering, 2008, 44(2):37-42.

[3] Sawalhi N,Randall R B. Vibration response of spalled rolling element bearings: observations, simulations and signal processing techniques to track the spall size[J]. Mechanical Systems and Signal Processing,2011,25(3): 846-870.

[4] Randall R B. Vibration-based condition monitoring: industrial, aerospace and automotive applications[M]. John Wiley & Sons, 2011.

[5] Epps I K. An investigation into vibrations excited by discrete faults in rolling element bearings[D]. Christchurch,New Zealand:The University of Canterbury,1991.

[6] Dowling M. Application of non-stationary analysis to machinery monitoring[R]. IEEE Paper, No. 0-7803-0946-4/93, 1993:159-162.

[7] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[8] Gao Q, Duan C, Fan H, et al. Rotating machine fault diagnosis using empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2008, 22(5): 1072-1081.

[9] Wu Z H，Huang N E．Ensemble empirical mode decomposition: a noise assisted data analysis method[J]．Advances in Adaptive Data Analysis，2009，1(1): 1-41．

[10] 陈仁祥, 汤宝平, 马婧华,等. 基于EEMD的振动信号自适应降噪方法[J].振动与冲击,2012,31(15):82-86.

CHEN Ren-xiang，TANG Bao-ping，MA Jing-hua. Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal [J]. Journal of Vibration and Shock, 2012,31(15):82-86.

[11] 郭瑜, 郑华文, 高艳,等. 基于谱峭度的滚动轴承包络分析研究[J]. 振动.测试与诊断，2011, 31(4): 517-521.

GUO Yu, ZHENG Hua-wen, GAO Yan, et al. Envelope analysis of rolling bearings based on spectral kurtosis [J]. Journal of Vibration，Measurement & Diagnosis, 2011, 31(4): 517-521.

[12] 石林锁, 沈金伟, 张亚洲,等. 基于 AR 模型和谱峭度法的滚动轴承故障诊断[J]. 振动与冲击, 2011, 30(12): 257-260.

SHI Lin-suo, SHEN Jin-wei, ZHANG Ya-zhou, et al. Fault diagnosis of a rolling element bearing based on AR model and spectral kurtosis [J]. Journal of Vibration and Shock, 2011, 30(12): 257-260.

[13] 苏文胜, 王奉涛, 张志新,等. EMD 降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3): 18-21.

SU Wen-sheng, WANG Feng-tao, ZHANG Zhi-xin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings [J]. Journal of Vibration and Shock, 2010, 29(3): 18-21.

基金项目：国家自然科学基金(51365023)

收稿日期：2014-11-12修改稿收到日期：2014-12-20

通信作者郭瑜 男，博士,教授，1971年12月生

中图分类号:TH133.33

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.01.004

Double-impulse feature extraction of faulty hybrid ceramic ball bearings based on EEMD

KONG You-bing, GUO Yu, WU Xing

(Kunming University of Science and Technology, Kunming 650500, China)

Abstract:Fatigue spalling is the most common cause of rolling bearing failure. When spalling failure occurs in a rolling ball bearing, the vibration acceleration signals have different features during rolling elements entering the spall area and leaving it. During rolling elements entering the spalling area, the signals are step responses, with mainly lower-frequency components, but during rolling elements leaving the spalling area, they are broader frequency impulse responses. The effective separation of the two features plays an important role in measuring the length of hybrid ceramic ball bearings’ spalling area. Here, an envelope extraction method based on ensemble empirical mode decomposition (EEMD) was proposed for the double-impulse extraction of faulty hybrid ceramic ball bearings. With this approach, firstly the auto-regressive(AR) model was used to pre-whiten the original vibration signals of feaulty hybrid ceramic ball bearings. Then, the pre-whitened signals were denoised based on EEMD. Lastly, Hilbert envelope extraction method was employed to extract the double-impulse. Simulation and tests were conducted respectively to verify the validity of the proposed method.

Key words:envelope analysis; EEMD; hybrid ceramic ball bearing; double-impulses; bearing fault

第一作者 孔佑炳 男，硕士生，1991年2月生