圆钢管混凝土压弯构件轴力——弯矩相关曲线分析及其应用

李仁哲，覃　浩，赵　鸣

(1.平壤建筑综合大学建筑工程系建设力学教研室，朝鲜 999093；2.同济大学土木工程学院，上海 200092)



圆钢管混凝土压弯构件轴力
——弯矩相关曲线分析及其应用

李仁哲1，覃浩2，赵鸣2

(1.平壤建筑综合大学建筑工程系建设力学教研室，朝鲜 999093；2.同济大学土木工程学院，上海 200092)

摘要：基于合理的钢材和核心混凝土拉压本构模型,利用截面分层法对钢管混凝土压弯构件轴力-弯矩-曲率进行全过程分析,建立了圆钢管混凝土压弯构件截面轴力-弯矩相关方程的计算公式和轴力-弯矩-曲率关系的实用计算方法，并对构件弹塑性状态下截面的弯矩-转角关系进行推导，进而提出了圆钢管混凝土柱塑性铰特性值的计算方法。

关键词：钢管混凝土柱;轴力-弯矩相关方程;塑性铰特性值

钢管混凝土具有承载力高、延性好、施工方便以及造价经济合理等优点，近年来在高层建筑和大跨度桥梁结构中得到广泛的应用[1]；实际工程中钢管混凝土受偏心荷载较常见，对钢管混凝土偏压构件进行研究有现实意义。关于圆钢管混凝土压弯构件截面数值计算的报道不少,丁发兴[2-4]、吝红育[5]、尧国皇[6]等在对钢管混凝土压弯构件截面进行数值分析的基础上，建立了钢管混凝土压弯构件截面轴力-弯矩-曲率关系实用计算方法，但文献[5]给出的计算公式过于简化，参数n0没有考虑到混凝土抗压强度。本文尝试通过理论推导给出n0的公式形式，再对数据进行拟合，以建立圆钢管混凝土柱压弯构件截面轴力-弯矩相关方程的理论计算公式。

该相关方程可以应用于在推导轴力-弯矩-曲率关系以及圆钢管混凝土柱塑性铰特性值的计算方法，此方程也可以用于圆钢管混凝土压弯构件弯矩-转角关系的计算。

1基本假设

对于钢管混凝土压弯构件截面分析，采用分层法计算模型，见图1。

图1　轴力-弯矩-曲率关系计算简图

图1中εc,k,εs,k分别为第k条带混凝土和钢管的轴向应变。

为简化分析，作如下基本假设:

1)平截面假定截面沿构件的轴向变形呈线性分布;

2)无滑移假定不考虑钢管与核心混凝土粘结滑移的影响;

3)无剪切假定钢管混凝土压弯构件变形以弯曲变形为主，忽略剪切变形的影响。

材料本构关系具体确定方法见文献[1]，以下为混凝土和钢材的本构关系。核心混凝土应力-应变曲线见图2。

图2　核心混凝土应力-应变曲线

压区混凝土的本构关系为:

σc=σ0[A(εc/ε0)-B(εc/ε0)2](εc≤ε0)

(1)

式(1)中：

σ0=σck[1.19+(13/fck)0.45(-0.074 85ξ2+0.578 9ξ)]

ξ0=1 300+14.93fck+[1 400+800(fck-

20)/20]ξ0.2

A=2-k,B=1-k,k=0.1ξ0.745

q=k/(0.2+0.1ξ)

式中:fck为混凝土抗压强度标准值，MPa;

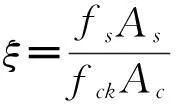
As、Ac为钢管混凝土横截面的面积。

拉区混凝土的本构关系为：

(2)

式(2)中：σp为峰值拉应力，σp=0.26(1.5fck)2/3;

εp为峰值拉应变，εp=43.1σp(με)。

在钢管应力为:

σ=

(3)

式(3)中：Es=2.06×105MPa

εc=0.8fy/Es,εc1=1.5εc,εc2=10εc1,

εc3=100εc1,A=0.2fy/(εc1-εc)2,

钢材应力-应变曲线见图3,fp、fy和fu分别为钢材的比例极限及屈服极限和抗拉强度极限；Es为钢材的弹性模量。

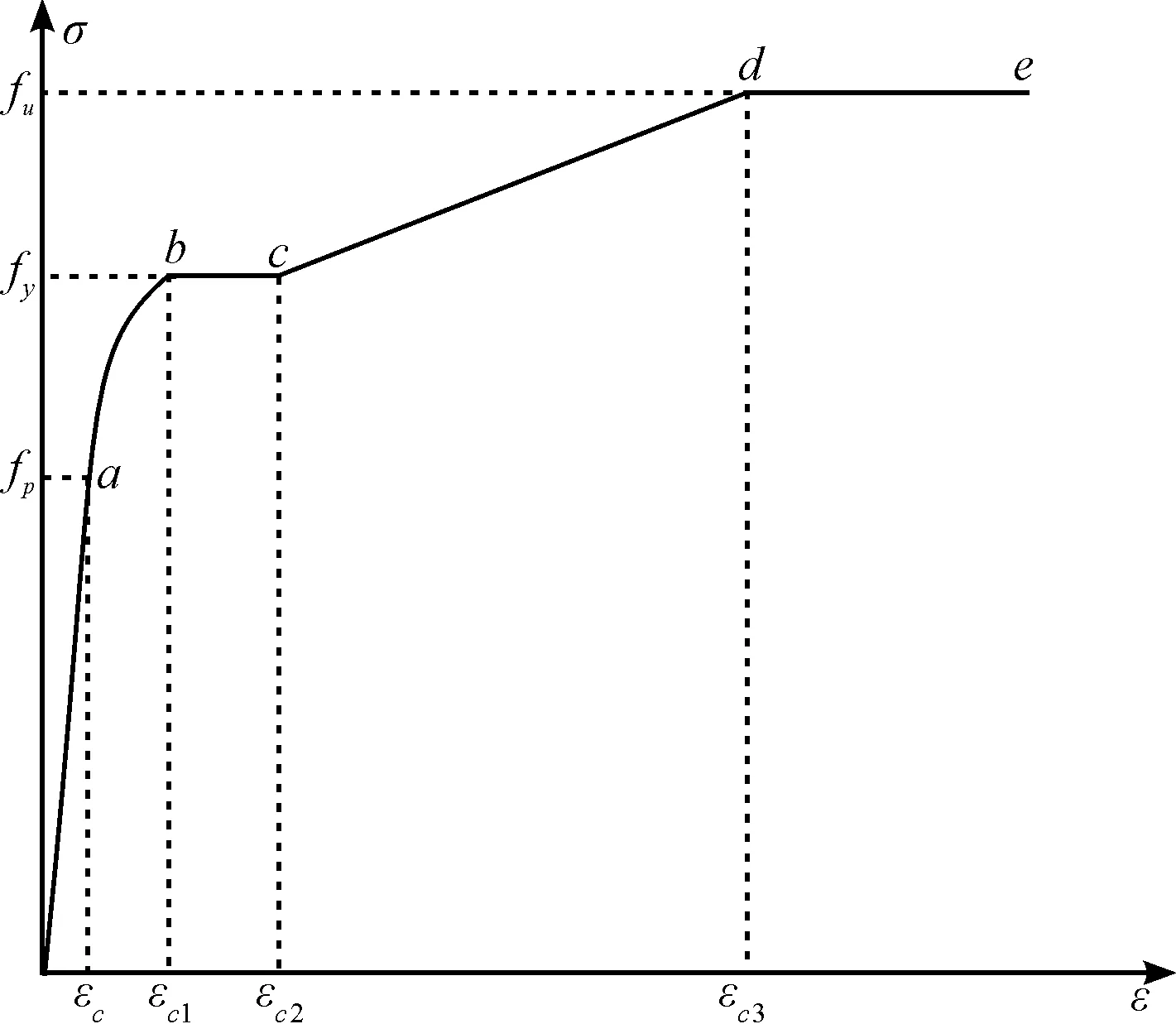
图3　钢材应力-应变曲线

2轴力-弯矩-曲率数值分析

钢管混凝土构件截面在轴力和弯矩作用下,设已知曲率为φ,由平截面假定可得到截面上任一点应变εk的计算公式

εk=ε0+ykφ

(4)

式(4)中:ε0为截面形心处的应变，yk为计算点的坐标。

因此

(5)

将截面划分为2n等分,每一段对应的圆心角为

dθ=2π/(2n)=π/n

θk=kdθ(k=1,2,…,n)

dAsk=(rc+t/2)tdθ

其中rc和t分别为混凝土的半径和钢管的壁厚。

由此可以得到该截面内弯矩

(6)

式(6)中:σc,k、σs,k分别为第k条带混凝土和钢管的轴向应力。

yck=rcsin(θk-0.5dθ)

ysk=(rc+t/2)sin(θk-0.5dθ)

内轴力

(7)

对于压弯构件截面，故应保证轴力Nin=N0(N0为钢管混凝土压弯构件截面上的外轴力)。

具体计算方法为:在给定截面曲率φ的情况下，通过调整截面形心应变ε0,当截面内轴力Nin等于外轴力N0时,计算得到截面弯矩Min。数值计算得到的典型钢管混凝土压弯构件截面N0-M-φ关系见图4。

na=N0/Nu

(8)

Nu为圆钢管混凝土轴压短柱的极限承载力。

Nu=Ascfscy

(9)

fscy=(1.212+Bξ+Cξ2)fck

(10)

式(10)中：对于圆钢管混凝土

B=0.175 9(fy/234)+0.974

C=-0.103 8(fck/20)+0.030 9

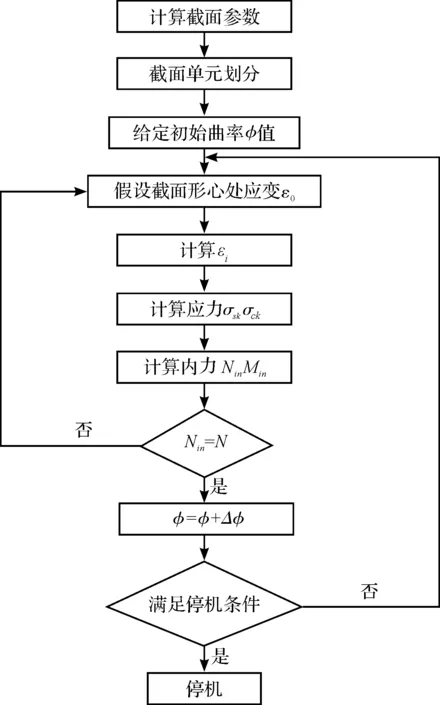
图4　计算步骤

3轴力-弯矩相关曲线计算公式

根据轴力-弯矩图形的形状，假设为抛物线，通过抛物线的一般公式可以得到下列关系式为

(11)

通过一系列计算推导可得计算公式形式为

(12)

式(12)中:

(13)

式(13)中：M0为压弯构件截面N0-M-φ曲线上的极限弯矩;

Mu为纯弯构件的极限弯矩；

n0为压弯构件截面极限弯矩M0=Mu时的轴压比；

Ncr为压弯构件达到极限弯矩时的轴力。

通过对由4组钢材屈服强度fy(Q235、Q345、Q390、Q420),4组混凝土强度等级(C30、C40、C50、C60),9组含钢率ρ(ρ=As/Asc,As和Asc分别为钢管截面面积和总的截面面积)和10组轴压比相互正交共2 880组工况的钢管混凝土压弯构件截面轴力-弯矩相关曲线参数分析,拟合钢管混凝土压弯构件截面轴力-弯矩相关实用计算公式。

(14)

式(14)中:ξ为套箍指数。

方差为0.000 6，变异系数为0.045。

4轴力-弯矩-曲率实用计算公式

通过对2 880组工况的钢管混凝土截面的参数分析，可以将钢管混凝土压弯构件截面N0-M-φ曲线用双折线进行拟合，见图6、图7。

图5　典型压弯构件截面N0/Nu-M0/Mu相关曲线图

图6　典型钢管混凝土N0-M-φ关系

(D=100 mm,t=1 mm,fy=235 MPa,C30,ξ=0.731 2)

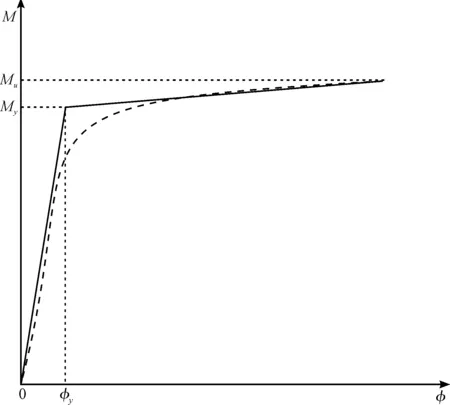
图7　钢管混凝土柱屈服弯矩定义

(15)

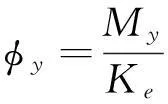
设My为屈服弯矩，My=0.89Mu，

Ke、Kp分别为钢管混凝土弹性阶段刚度和强化阶段刚度,见文献[1]。

Ke=0.216Mu/φe,φe=0.416fy/(EsD)

Kp=αpKe,αp=0.018+0.026n-0.012n2

n压弯构件为轴压比。

5M-θ关系曲线

将上述M-φ关系曲线，转化为M-θ关系曲线，假定:

1)单元内弯矩沿杆件为线性分布;

2)弹塑性变形集中于构件的两端区域;

3)反弯点位于构件的中点。

根据假定，取杆件长度一半作为计算转角的简化模型，以反弯点为坐标原点如图7所示。沿杆件方向，构件截面弯矩由0不断增加至Mu的过程中，其截面状态划分为两个区段:

1)当杆件端A截面达到屈服弯矩My时，此构件各截面状态均为第I区段，见图8a)所示。

图8　杆件M-φ分布图

在杆件的任何处曲率为：

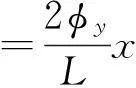
边界条件

由此

杆件端截面转角θA为

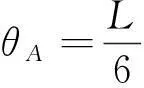
2)当杆件端A截面达到极限弯矩Mu时，构件曲率弯矩分布为第Ⅱ区段，见图8b)。

对曲率进行分段积分可求得构件的相对转角。

在杆件的任何处曲率为：

其中

杆件端截面转角θA为：

通过上述过程将钢管混凝土构件的M-φ关系转化为以M-φ表述的本构关系，并进一步转换为以M/My为横坐标、θ/θy为纵坐标的塑性铰本构关系的曲线形式。

6结语

1)基于数值分析和理论推导，建立了钢管混凝土压弯构件截面轴力-弯矩相关曲线实用计算公式和钢管混凝土压弯构件轴力-弯矩-曲率关系实用计算公式。该公式比文献[5]得出的公式均值更接近1，且方差更小，采用工况数也更多。

2)根据钢管混凝土压弯构件的弯矩-曲率曲线，对钢管混凝土压弯构件弹塑性状态下截面弯矩-转角关系进行推导,给出了钢管混凝土压弯构件塑性铰特性值的计算公式。该公式可以用于各软件中确定钢管混凝土柱塑性铰特性值[7]。

参 考 文 献

[1]韩林海.钢管混凝土结构[M].北京:科学出版社,2000.

[2]丁发兴,余志武，蒋丽忠.圆钢管混凝土结构非线性有限元分析[J].建筑结构学报,2006,27(4):110-115.

[3]丁发兴,余志武.钢管混凝土基本力学性能研究-实用计算方法[J].工程力学,2005,22(3):134-138.

[4]丁发兴,张鹏,余志武,等.圆钢管混凝土截面轴力-弯矩-曲率关系实用计算方法[J].哈尔滨工业大学学报，2009(12):133-137.

[5]吝红育.基于Pushover理论的钢管混凝土构件塑性铰特性值研究[J].郑州大学学报：工学版,2013(5):7-11.

[6]尧国皇,韩林海.钢管混凝土轴压与纯弯荷载-变形关系曲线实用计算方法研究[J].中国公路学报，2004,17(4):50-54.

[7]北京金土木软件技术有限公司.Pushover分析在建筑工程抗震设计中的应用[M].北京：中国建筑工业出版社，2010.

收稿日期：2016-01-18

作者简介：李仁哲(1971—)，男，朝鲜民主主义人民共和国人，教师，同济大学土木工程学院结构工程专业高级进修生。

中图分类号：TU398

文献标志码：A

文章编号：1008-3707(2016)05-0011-05

Analysis and Application of the Correlation Curve of AxialForce Bending Moment for the Beam——Columns ofCircular Steel Tube Concrete

LI Renzhe1, QIN Hao2, ZHAO Ming2