DEM地形描述误差的概率分布特征研究

杨灿灿，王　春，江　岭，钟文军

(1.滁州学院 地理信息与旅游学院，安徽 滁州 239000;2.滁州学院 安徽省地理信息集成应用协同创新中心,安徽 滁州 239000)



DEM地形描述误差的概率分布特征研究

杨灿灿1，2，王春1，2，江岭1，2，钟文军1，2

(1.滁州学院 地理信息与旅游学院，安徽 滁州 239000;2.滁州学院 安徽省地理信息集成应用协同创新中心,安徽 滁州 239000)

摘要：：以黄土丘陵1:1万DEM为基础数据，通过稀疏抽点法获取不同格网点布设位置下的DEM，进而分析不同分辨率DEM中单个地面点和区域地形单元的Et概率分布特征。实验结果表明：对于任意格网分辨率DEM，无论是不同布设方案下的单个地面点，还是区域地形单元，其Et的概率密度均呈现正态分布特征。对于单个地面点，如果以其为中心的3×3DEM格网单元区域以凸地形为主，其Et概率密度呈现出右偏正态分布特征；如果以凹地形为主，则呈现左偏正态分布特征,其他区域则呈现标准正态分布特征。

关键词：DEM;地形描述误差;概率分布;正态分布;误差场

DEM地形描述误差(简称Et)指在DEM格网点高程采样误差忽略不计的条件下，由DEM离散格网采样点重构的，模拟地形表面与自然地形表面点之间存在的高程偏差[1]。随着现代高分对地观测技术的不断发展，DEM误差研究的日益深入，Et已逐步成为影响国家系列比例尺DEM质量的主要因素[1-7]。汤国安、王光霞等对地形描述精度进行研究，并建立区域Et中误差的初步估算模型[8-9]。王耀革、Chen C F、赵牡丹等研究指出Et具有与地形部位显著相关的空间结构性分布特征，并与地形因子等密切相关[10-14]。王春等研究指出，对于任意已知格网分辨率DEM，其Et的空间分布是一个围绕实际地形上下波动且具有特定厚度的误差壳[15]。据此可以预见，对于任意已知格网分辨率DEM，随着DEM格网点实际布设位置的不同，任意一点在其垂直方向具有无穷多不同大小的Et值，揭示其概率分布特征，有望建立Et等概率面模型，进而实现顾及Et空间分布特征的DEM数字地形分析不确定性的推演。鉴于此，本文以黄土丘陵1∶1万DEM为基础数据，采用重采样法生成不同格网分辨率DEM，从单点和区域视角进行Et的概率分布研究，剖析其在误差壳中的概率分布特征，进一步完善和发展DEM误差分析理论与方法。

1Et数值解算模型及检验模型

1.1Et数值解算模型

假定P的实际高程为hp，在当前格网分辨率DEM中的高程为Hp_i。对于任意一点P的Eti(i为不同DEM格网布设方案的编号)值被定义为

(1)

如图1所示(虚线框为包含P点的不同位置DEM的格网线)，假定参考真值DEM的格网分辨率为d，待分析的DEM格网分辨率为kd，对于任意一地面点P，只要当前DEM格网的左下角点位于ABCD实线矩形框内，则地面点P均属于虚线所示DEM格网单元内部的点。显然，地面点P与实际DEM格网有着无穷多的位置关系，其Et值也会随着实际DEM格网点布设位置的不同而不断改变，对此，文献[16]提出了支持不同DEM布设方案的Eti计算模型。

图1　地面点P与DEM格网间位置关系

首先，以高分辨率DEM为参考真值，采用抽点法获得其他分辨率不同位置的DEM数据。如图2所示，在格网分辨率为d的参考真值DEM基础上，采用抽点法获得2d格网分辨率的DEM，则总共可有4种格网布设方法；采用抽点法获得3d格网分辨率的DEM，则总共可有9种格网布设方法。以此类推，如果采用抽点法获得kd格网分辨率的DEM，则总共可有k2种格网布设方法。然后，采用以4×4 DEM格网单元为搜索圆的完全规则样条函数插值模型，计算出P点在DEM地形曲面上的高程Hp_i，减去P点在参考真值DEM中的高程hp，完成Eti的解算。

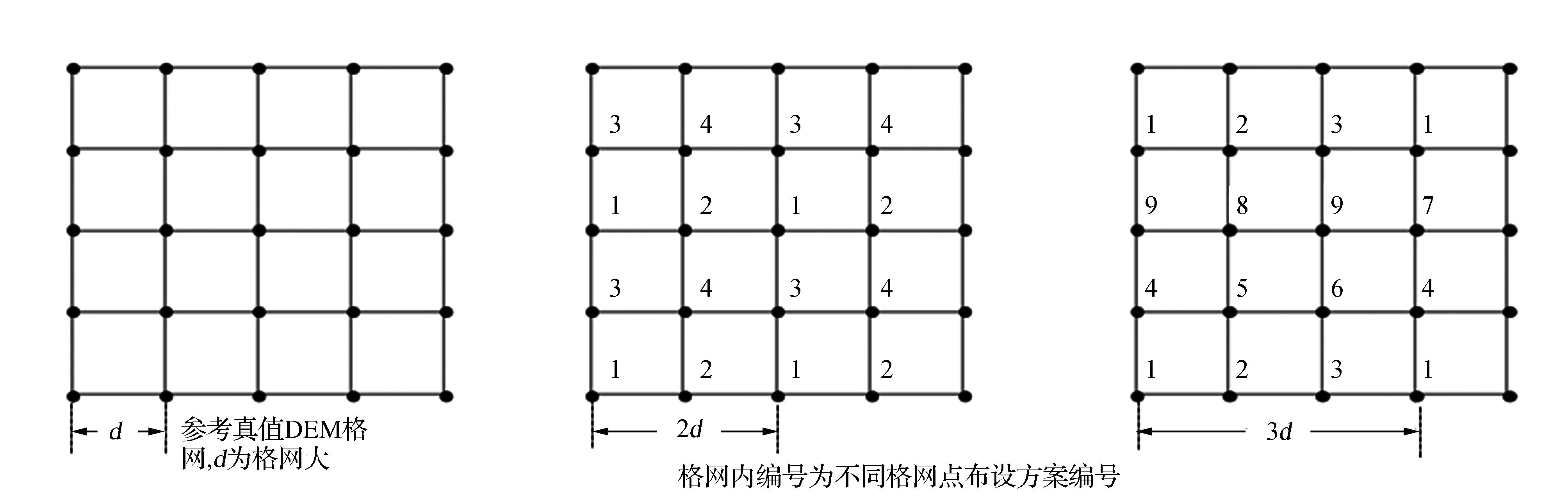
图2　不同基准点位置的DEM格网布设方案示意图

1.2Et数值概率分布检验模型

对于Et数值概率分布特征单样本参数进行的检验是建立在总体服从一定分布假设的基础之上。本文首先假设Et数值概率分布特征服从正态分布，借鉴DEM精度评定的经典方法——等高线套合法，通过数据序列构成的分布曲线与假设分布曲线进行套合对假设进行检验。统计假设检验模型是统计学中的常用方法，亦可验证Et数值概率密度函数是否服从正态分布，进而本文利用Kolmogorov-Smirnov(K-S)检验模型以及Q-Q图检验模型进行假设检验。

K-S假设检验是将一组样本值的分布和某一指定的理论分布函数进行比较，确定两者之间的符合程度[17]。假设样本Xi来自正态总体，F(x)表示理论分布的分布函数，Fn(x)表示一组随机样本的累积频率函数，D为二者差距的最大值，则有

(2)

当实际观测D>D(n,α)，则拒绝假设；反之则接受其为正态分布，其中D(n,α)是显著水平为α，样本容量为n时，D的拒绝临界值。为方便起见，统计软件直接输出在该统计检验值下得出的相伴概率P值，并与显著性水平α作比较，进而得出拒绝或是接受假设的结论。

若把观测数据从小到大排列x(1)≤x(2)≤…≤x(n)，则经验分布函数为

(3)

式中：k为数据从小到大排列的序号。由于理论分布函数近似等于样本经验分布函数，有

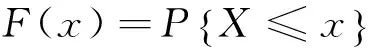
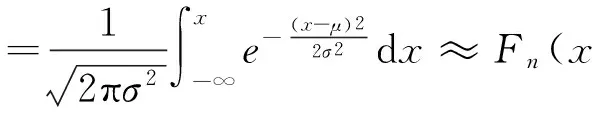
(4)

式(4)中σ表示标准差，μ为期望，若记标准正态分布的函数为Φ(x)，则

(5)

故在Oux平面上，有

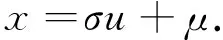
(6)

2实验与结果分析

2.1实验数据

实验样区位于陕西省绥德韭园沟，韭园沟地处水土流失严重的陕北黄土高原，地表形态主要由梁、茆和分割梁茆的沟谷组成，平均坡度28.6°，平均地形起伏度7.49 m，此地区最低高程为848.697 m，最高高程为1 132.31 m。图3为实验区DEM影像。

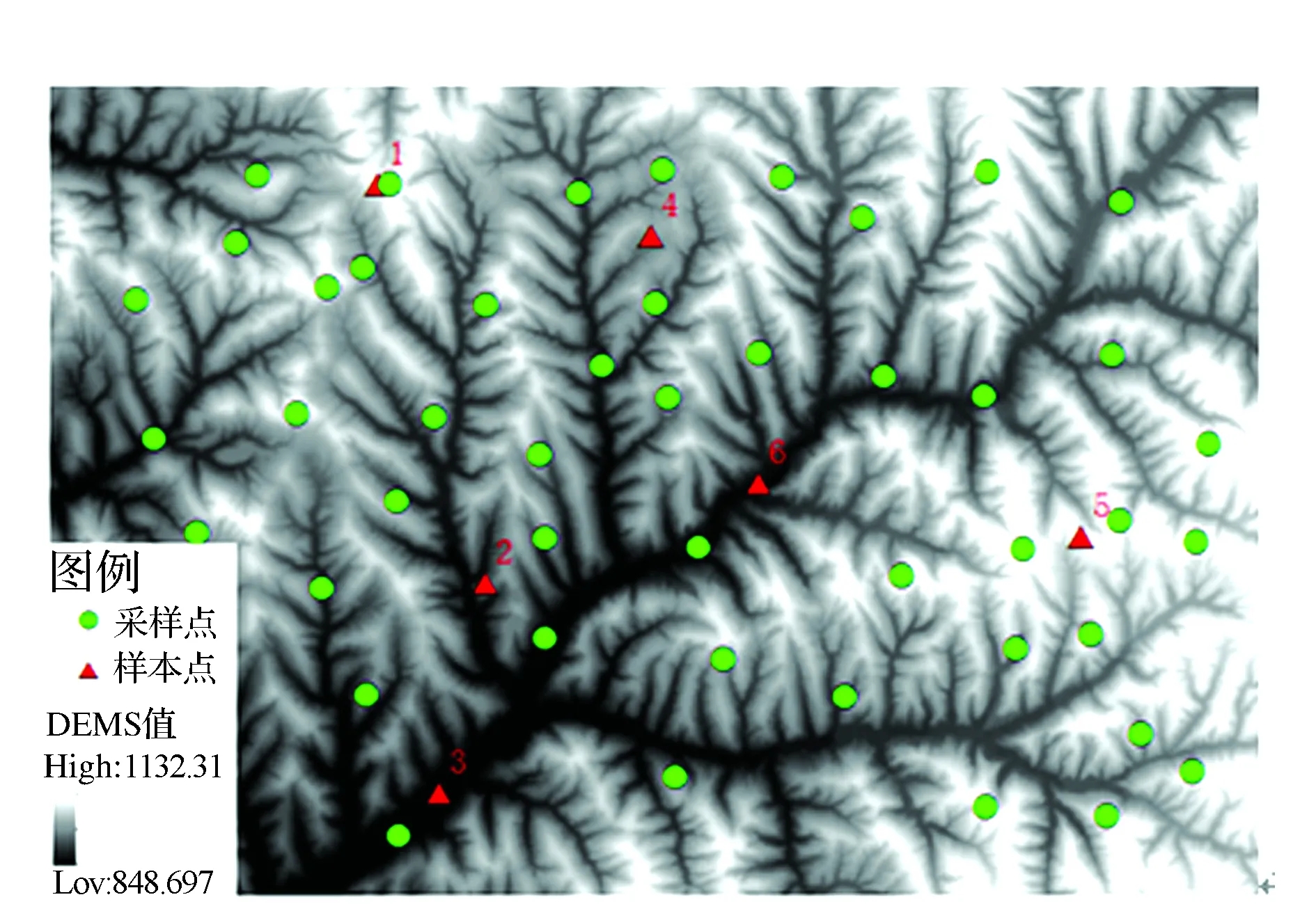
图3　试验区DEM及采样点示意图

本文以实验区1∶1万DEM为基础数据，通过稀疏抽点法获取不同格网布设位置且格网分辨率分别为5 m，15 m，25 m，35 m，…,125 m的DEM数据，进而通过Et值解算模型分别获取其Et值信息，其中5 m为参考真值。

2.2单地面点Et数值变化特征

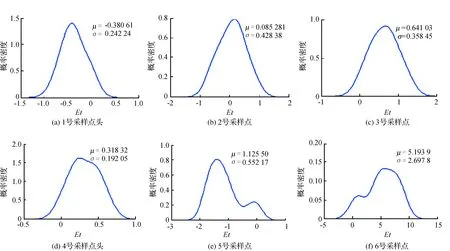
在研究区域中随机选择54个地面采样点(如图3所示)，以25 m DEM为例通过上文布设方案得到每一个地面采样点在25种格网位置关系下的地形描述误差Eti值，并对其进行统计分析，统计结果如图4所示(此处只选6点进行展示)。图中曲线为Et概率密度函数曲线，横轴表示Et值，纵轴表示概率密度，即对应横轴值得到的Et概率密度函数值。

Et概率密度函数曲线图显示单点在不同布设方案下的Et值统计特征近似服从正态分布。本文假设此系列Et值服从标准正态分布，继而以1号采样点为例通过标准正态分布曲线套合法以及SPSS统计检验法分别对此假设进行检验。

1)曲线套合法：对任意一点对应的25个Et值求期望和方差，画出正态概率密度函数曲线并与此点的概率密度函数曲线进行套合。实验证明，两条曲线趋势相同(如图5(a)所示)，且在波动允许的范围内可用同一函数进行描述，即此组数据近似服从标准正态分布。

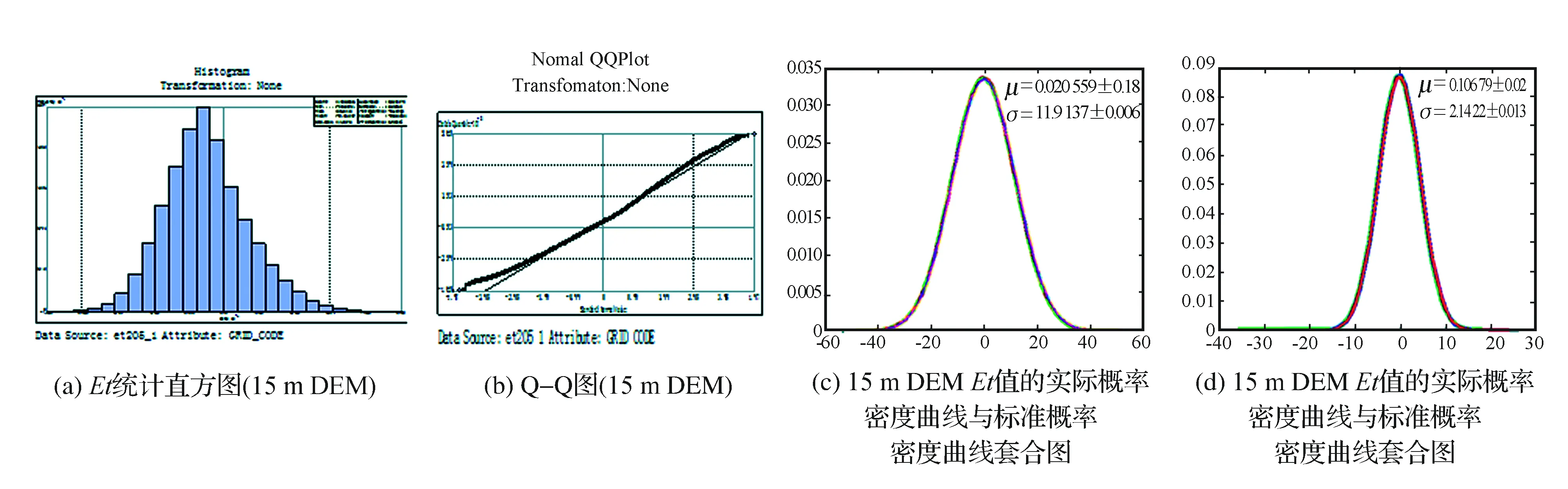
2)K-S检验：在SPSS中，利用非参数检验K-S方法得出相伴概率值P，并与显著性水平0.05进行比较。实验结果表明P值为0.773大于0.05，D为0.132，查表可得D(n,α)=0.264，D

3)Q-Q图检验：依据Q-Q图检验方法，以样本的分位数作为横坐标，以按照正态分布计算的相应分位点作为纵坐标，在上述平面坐标系中做散点图，经实验样本点成围绕第一象限对角线的直线分布，说明此数据服近似服从标准正态分布，Q-Q图如图5(b)所示。

图4　Et分布概率密度曲线

图5　单地面点Et值服从正态分布统计规律的检验

在进行凸地形为主的5号点和以下凹地形为主的6号点进行正态分布检验时，发现5号点的P值为0.663大于0.05，D值为0.146小于D(n,α)，偏度系数Skewness为0.944大于0且偏度较大，说明此数据为正态分布呈右偏状态。6号点中，偏度系数为-0.503小于0，说明此组数据服从左偏态分布。具体分析则会发现，以地面点为中心的3×3 DEM格网分辨率下，若以上凸地形为主，地面起伏较大时，格网间隔大于凸起地形的一半，或者是格网间隔恰巧包含了地形凸起部分，则会使DEM的描述值小于真实地形的高程，从而使地形描述误差绝对值较大且Et值表现为右偏态；同样，在下凹地形中，DEM格网间隔大于地形中两高峰之间的距离，或者下凹地形长度恰为格网间隔，则会使概率密度曲线表现为朝向偏左的偏态分布。

利用同一方法，对其余地面采样点进行正态分布统计假设检验，结果表明实验区内任意单一地面点在不同布设方案下的Et值，以其为中心的3×3 DEM格网分辨率区域以上凸地形为主，其Et概率密度呈现出右偏正态分布特征；如果以下凹地形为主，则呈现出左偏正态分布特征；其他区域则呈现标准正态分布特征。

2.3区域地形单元Et概率变化特征

单点Et数值的变化特征能够为等概率面的构建提供前提和基础，但是还需从整体上研究区域地形单元Et概率变化特征，从而科学有效的进行Et误差传播和不确定性应用研究。本文以5 m、15 m格网分辨率为例进行区域地形单元的Et概率变化特征的分析。

图6(a)为格网分辨率15 mDEM中区域地形单元的Et数值统计直方图，通过目视可以看出Et的统计规律近似服从正态分布，由统计指标偏度系数为0.344，图6(b)Q-Q图中各点表现为围绕对角线近似直线分布，此数据服从正态分布统计特征。利用此方法分别对不同布设方案下的Et值进行实验，结果表明在15 m格网分辨率下，区域单元地形描述误差的期望和标准差会因布设方案的不同略微变动，但是整体的地形描述误差服从正态分布，而且可以用期望为-0.02，方差为11.916 7的概率密度函数来描述。不同布设方案下区域单元Et值的概率密度曲线叠加情况见图6(c)，其中±0.18以及±0.06分别表示期望和方差的波动范围。

图6　区域单元Et值服从正态分布统计规律的检验

选取5 m DEM，利用相同的方法对研究区域内Et值进行分析，结果如图6(d)所示。此图说明5 m格网分辨率下，期望和方差也会因布设方案的不同而有所变化，期望的变化范围为±0.02以及±0.013，区域地形单元Et数值的变化特征可近似用期望为-0.108 8，方差为2.142 2的概率密度函数表示。利用相同的方法对其他任意格网分辨率下的区域地形单元Et数值进行分析，结果表明，区域地形单元Et的概率密度均呈现理想的正态分布特征。

3结束语

基于Et解算模型，获取了任一地面点在不同格网分辨率及不同格网位置下的Et值，在此基础上分别对单点和区域单元的Et值进行概率分布及数值变化特征分析。实验结果表明：对于任意确定格网分辨率的DEM，无论是单点Et值，还是区域单元的Et值，均近似服从正态分布；同时在以当前地面点为中心的3×3 DEM格网分辨率范围内，当其地表曲面呈现显著的以凸地形为主(或以下凹地形)为主时，Et值的概率分布曲线也会在出现一定的右偏态(或左偏态)的现象，其余皆服从正态分布。

依据Et值正态分布特点，由1σ，2σ，3σ，……不同倍率的Et标准差，构建Et误差壳等概率面模型，将为实现顾及Et空间场分布特征的DEM数字地形分析误差传播推演奠定基础。然而，要实现完整意义的上述误差传播推演，还需在等概率面基础上研究揭示Et值在横向空间相关性特征，即各格网单元Et值与其相邻格网单元Et值之间的空间相关关系。

参考文献：

[1]TANG G A. A sensitivity analysis of errors in digital terrain models[D]. Salzburg: Salzburg University,1998.

[2]KINGDER D B.High-order Interpolation of Regular Grid Digital Elevation Models[J].Inernational Journal of Remote Sensing,2003,21(14):2981-2987.

[3]FISHER P F, TATE N J.Causes and Consequences of Error in Digital Elevation Models[J].Progress in Physical Geography,2006,30(4):467-489.

[4]王春,刘学军,汤国安,等.格网DEM地形模拟的形态保真度研究[J].武汉大学学报(信息科学版)，2009,34(2):146-150.

[5]胡海, 吴艳兰, 胡鹏. 数字高程模型精度标准、质量理论和科学观念讨论[J]. 武汉大学学报(信息科学版),2011,36(6):713-717.

[6]张朝忙，刘庆生，刘高焕，等.中国地区SRTM3 DEM高程精度质量评价[J].测绘工程，2014,23(4)：14-19.

[7]OKSANEN J,SARJAKOSK T.Uncovering the statistical and spatial characteristics of fine toposcale DEM error[J].Phptogrammetric Engineering and Remote Sensing,2006, 57(10):1329-1332.

[8]汤国安,龚健雅,陈正江,等. 数字高程模型地形描述精度量化模拟研究[J].测绘学报, 2001, 30(4):361- 365.

[9]王光霞，朱长青，史文中，等. 数字高程模型地形描述精度的研究[J].测绘学报,2004,33(2)：168-173.

[10] 王耀革，王志伟，朱长青.DEM误差的空间自相关特征分析[J].武汉大学学报(信息科学版)，2008，33(12):1259-1262.

[11] CHEN C F, YUE T X.A method of DEM construction and related error analysis[J]. Computers& Geosiences,2010,36(6):717-725.

[12] 汤国安,赵牡丹,曹菡. DEM地形描述误差空间结构分析[J].西北大学学报(自然科学版), 2000, 30(4):349-352.

[13] 贾敦新，汤国安，王春，等.DEM数据误差与地形描述误差对坡度精度的影响[J].地球信息科学学报，2009,11(1):43-49.

[14] 刘春，孙伟伟，吴杭彬.DEM地形复杂因子的确定及与地形描述精度的关系[J].武汉大学学报(信息科学版)，2009，34(9)：10105-1019.

[15] 王春，汤国安，戴仕宝，等. DEM地形描述误差场量化分析研究[J]. 武汉大学学报(信息科学版)，2014,39(9)：1074-1079.

[16] 王春，顾留碗，陶旸，等. DEM地形描述误差(Et)计算模型研究[J]. 地球信息科学学报，2014,18(5)：699-708。

[17] 王星.非参数统计[M].北京：清华大学出版社，2010.

[责任编辑：李铭娜]

DOI:10.19349/j.cnki.issn1006-7949.2016.08.005

收稿日期：2015-09-07

基金项目：安徽省自然科学基金资助项目(1408085MD77);教育部科学技术研究重点项目(212078);安徽省高校自然科学研究一般项目(KJ2015B13);滁州学院科研基金资助项目(2014KJ02)

作者简介：杨灿灿(1988-)女，硕士，助教.

中图分类号：P208

文献标识码：A

文章编号：1006-7949(2016)08-0019-05

Probability distribution characteristics of DEM terrainrepresentation error

YANG Cancan1,2, WANG Chun1,2, JIANG Ling1,2，ZHONG Wenjun1,2

(1.Geographic Znformation and Tovrism College,Chuzhou University,Chuzhou 239000,China;2.Anhui Center for Collaborative Innovation in Geographical Information Integration and Application, Chuzhou University, Chuzhou 239000, China)

Abstract：Taking a 1∶10 000 DEM of loess hill as the source data, this paper analyzes the probability distribution characteristics of Et for individual points and regional terrain units via getting DEMs with different layout schemes through sparse resampling technique. Experimental results show that:for any resolution of DEM, the probability density of Et appears in the characteristics of a normal distribution, no matter it is gotten from individual points or regional terrain units;for a single ground point, if located in an area corresponding to 3×3 grid cells with this point as the center and this area has mainly a convex terrain on the earth, the probability density of Et shows a right skewed normal distribution. If this area corresponds mainly to a concave surface, the probability density of Et shows a left skewed normal distribution, and it shows a standard normal distribution for the area with other surface forms.

Key words：DEM; terrain representation error; probability distribution; normal distribution; error field