基于控制向量参数化和迭代凸规划的无人机编队飞行的建立

过娟, 褚晶, 闫杰

(1.西北工业大学 航天学院, 陕西 西安　710072; 2.西北工业大学 航空学院, 陕西 西安　710072)



基于控制向量参数化和迭代凸规划的无人机编队飞行的建立

过娟1, 褚晶2, 闫杰1

(1.西北工业大学 航天学院, 陕西 西安710072; 2.西北工业大学 航空学院, 陕西 西安710072)

摘要：多个无人机组成的编队飞行可以作为很多应用中现有技术的一种高效、低成本的替代方案。研究了能满足最终编队队形约束的且能量最优的无人机编队飞行的建立。首先，将编队建立问题建模成一个受非线性动力学约束的能量最优控制问题。其次，采用直接法来求解该最优控制问题。在采用的直接法中，利用控制向量参数化方法将原始问题转化成一系列待求解的凸优化问题；然后，运用迭代凸规划(SCP)技术求得其最优解。在求解过程中，SCP迭代的每一步本质上都是一个二次型规划问题；由于该规划问题的约束是线性约束，因此可以高效地进行求解。最后，将提出的方法运用到3个无人机的V型编队建立中，并使用了免费的开源求解器CVX进行求解。与MATLAB中提供的全局优化技术相比，文中提出的算法能够快速地收敛到全局最小值。

关键词：无人机编队飞行；最优控制；控制向量参数化；迭代凸规划

编队飞行中的多个无人机(UAVs)可以通过相互协作实现单个无人机无法完成的复杂任务。因此，对现存的很多技术而言，多个无人机的编队飞行，特别是小型无人机的编队飞行，是一个前景广阔且成本很低的替代方案，能够在很多领域得到广泛应用，例如国土测绘、海洋勘探、高速公路/石油/天然气/电力线路巡检、气象/环境监测、警用巡逻、灾情防护、应急救援、公共安全、通信中继等[1]。

然而，在许多应用中，为了能实现之后的协同操作，多无人机首先需要建立起所需的编队。例如，一组无人机从一个小型跑道起飞后，通常会形成一个直线编队[2]。然而为了执行某个侦察任务，则要求一个V型编队以降低被敌方雷达发现是多架飞机的概率。因此，这组无人机需要根据当前的飞行状态建立起任务所需的V型编队。该编队的建立过程通常被要求是能量最优的，使得全局能量消耗最小；或者是时间最优的，使得系统快速具备空中作业的能力，例如，快速实现对森林火灾的监控为消防单位提供宝贵的灾情信息。此外，编队的建立还需满足各种约束。这里主要有2种类型的约束。一种是局部约束，例如动力学约束、状态约束、控制输入约束、避障约束等；另外一种是耦合约束，这种约束与编队中的其他无人机相关联，例如无人机之间的避撞约束、通信网络拓扑约束、最终编队队形约束等。

本文研究了典型的局部约束和耦合约束下，能量最优的无人机编队飞行的建立。在本文的研究中，局部约束包括状态约束、控制约束和非线性动力学约束。与线性动力学约束相比，非线性动力学约束更加复杂，这是因为线性动力学的解可以通过解析推导获得[3]。同时，对于典型耦合约束，本文考虑了最终队形约束。在本文中，最终队形约束不仅约束无人机的最终状态，同时也存在着待确定的未知参数。例如，为了建立一个V字型编队，最终队形约束只设定了无人机之间的最终相对位置，然而在空间什么位置建立起所需编队却作为待优化的未知参数进行求解。

一般地，可以将编队的建立建模为开环最优控制问题，然后采用直接法或间接法进行求解[4-5]。直接法将最优控制问题转换为参数优化问题进行求解，而间接法利用由变分法推导出的解析必要条件进行求解。然而，对于存在终端约束的编队建立(例如，最终编队队形约束)，间接法不再适用，这是因为此时由最优一阶必要条件得到的两点边值问题(TPBVP)的解很难求得[4-5]。相反地，直接法更加适合求解此类问题，因为编队建立问题被直接转换为参数优化问题后，可由各种成熟的非线性规划(NLP)求解器求解。

本文的目的便是为多无人机的编队建立设计一个基于直接法的最优控制算法。为实现这一目标，我们利用控制向量参数化方法将原问题转化为参数优化问题。在控制向量参数化方法中，时间域被划分成有限个子区间，且在每个子区间中，控制量被近似为一个分段常值参数[6]。之后可利用诸如龙格-库塔法进行非线性动力学方程的求解。这样，原始最优控制问题就可以被转换为一个非线性规划问题，而非线性规划问题可通过多种技术求解。本文采用迭代凸规划(SCP)技术对其进行求解，这主要是因为SCP简单、高效且是免费开源的[7]。而在运用SCP之前，需要推导出状态约束和最终编队约束相对于优化变量的梯度。本文采用灵敏度法求得上述梯度，主要原因是灵敏度法精度较高并且便于实现。在本文提出的方法中，SCP迭代的每一步本质上是一个受线性约束的二次型规划问题。对于这种问题，如果采用定制的而非标准的优化算法，求解速度可以提高2～3个数量级[8]。

1编队建立问题的建模

在本节中，将受非线性动力学约束，且能量最优的多无人机编队的建立建模成一个最优控制问题。在问题建立之前，首先设定本文研究的背景。

1.1研究背景

假设现在有n个无人机在三维空间中自由飞行。而由于任务要求的改变,需要这n个无人机建立一个编队,且该编队需满足最终几何约束,即最终队形约束。这些几何约束可以由1组未知参考参数和相应设定的差量确定。例如,在V型编队约束中,参考参数是编队建立的空中位置,而相应差量是每个无人机相对于该位置的相对位置。因此,只需要对参考参数进行优化。除了参考参数的优化之外,编队的建立还需要在规定的时间内完成并尽可能少地消耗能量。另外,在此过程中,无人机的状态变量必须满足非线性动力学约束,控制输入也要满足无人机平台的控制输入约束,并且每个无人机的状态变量应该始终保持在它们的规定范围域内。

在本文研究中,无人机飞行的非线性动力学方程表示如下[9]

(1)

式中,Xi=[xi,yi,zi,θi,ψi]T是第i个无人机的状态变量,Ui=[ui1,ui2]T是控制向量,(xi,yi,zi)是第i个无人机的坐标,Vi是该无人机的飞行速度,设定为常值,θi和ψi分别是第i个无人机的攻角和方向角,ui1和ui2分别控制第i个无人机的攻角和方向角。

1.2编队建立问题的建模

将能量最优的无人机编队飞行的建立建模为最优控制问题。目标函数为最小化系统总能量的消耗

(2)

该最优控制问题受到的约束有:(1)式中所示的动力学约束

(3)

控制输入约束

(4)

初始边界条件约束

(5)

状态约束

(6)

以及最终编队队形约束

(7)

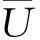
2编队建立的最优控制

如同之前所阐述的,能量最优问题的建立是采用直接法的第一步。在本节中,首先将之前建立的最优控制问题转换成一个非线性规划问题,这一步采用控制向量参数化方法实现;其次,确定状态约束和最终编队约束相对于所有优化变量的梯度;最后将能量最优控制问题近似为SCP问题进行求解。

2.1控制向量参数化

为了求解1.2节中建立的问题,根据标准的控制向量参数化方法将控制向量近似成一个分段常值函数。首先,将时间区间[t0,tf]分成N个相等的子区间,其中各个时刻满足

之后,在每一个时间段,将第i个无人机的控制向量Ui做如下的近似

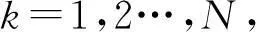
(8)

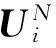
(9)

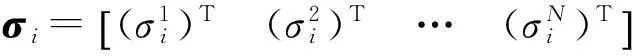
控制参数化后,可以重新建立能量最优控制问题。将(9)式带入(3)式,动力学方程可以写为

(10)

初始条件在(5)式中给出。类似地,(4)式中显示的控制约束可转变成对σi的约束,即

(11)

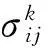
对于第i个无人机,将满足(11)式的所有σi的集合记作Ξi。对每个无人机而言,当给定一个σi∈Ξi,就可以利用(5)式中给出的初始条件求解(10)式,从而得到Xi(τ)。实质上,这是一个初始值问题(IVP),而求解该问题的计算方法已经相当成熟[10]。大部分方法可以被归纳为单步法,例如龙格-库塔(RK)方法,或者多步法,例如求解非刚性问题的Adams-Bashforth法,以及求解刚性问题的向后差分法(BDF)。另外一类求解初始值问题的方法是基于配置法,它通过一个分段多项式近似每个子区间的状态变量[11]。一旦计算得到无人机飞行轨迹的解,就可以重新建立最终编队队形约束,如下

(12)

式中,Xi(tf|σi)是给定N个子区间对应的分段常值控制参数后求得的第i个无人机的最终状态解;显然,它是σi的函数。

至此,可以将编队建立问题重新写成一种简单形式。该形式便于处理状态约束和最终队形约束:

(13)

2.2梯度计算

本文采用灵敏度法计算状态约束和最终队形约束相对于ξ的梯度。由于状态约束和最终队形约束都是ξ的隐函数,使得梯度的计算更加复杂。在文献中,这些梯度通常被称作敏感变量。

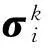
对于每个无人机i,给定一个σi∈Ξi,对(10)式积分计算即可求得任意τ∈[τk-1,τk)时的状态变量。

(14)

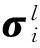
(15)

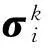
(16)

(17)

这样,在区间[τk-1,τk)内,可以通过(15)～(17)式对τ求导从而可以得到计算∂Xi(τ|σi)/∂σi的辅助方程如下

(18)

为了计算∂Xi(tf|σi)/∂σi,需要对(18)式在整个时间区间[0,tf]进行积分,且积分初始状态为

(19)

在本文研究中运用龙格-库塔法来求解推导出的初始值问题,这仅仅是因为该方法在解决后面算例时的高效性和准确性,然而对于特定的问题可以选择特定的方法。因此,可以采用更加合适的方法来解决具体的刚性或非刚性问题。注意,在对(18)式积分的过程中,需要用到求解(10)式得到的状态信息,因此需要联立进行求解。由于同时求解状态方程和辅助方程,因此可以对状态变量和敏感变量同时施加一个局部控制误差以提高解的精度。

2.3迭代凸规划方法

一旦目标约束和最终编队队形约束相对于优化变量的梯度已知,在文献中通常采用NLP技术中的SQP或者内点法求解问题(13)。然而,在本文中,选择SCP技术是因为它简单、高效且是免费开源的。

SCP的基本思想是通过迭代求解原始问题的凸逼近序列来求解问题(13)。在问题(13)中,只有状态约束和最终队形约束需要进行近似,而由于它们相对于优化变量的梯度可以积分求得,因此可以采用一阶泰勒展开进行近似。对于第k个序列,利用下面给出的问题(20)以及优化变量ξ来近似问题(13)。明显地,问题(20)是一个凸优化问题。在问题(20)中,所有的偏微分以及所有无人机状态Xi,k都可以利用前面小节中推导出的方程计算得到。在问题(20)中,为了保证初始猜测值任意选择时的全局收敛性,需要将一个信任域(trustregion)施加在ξ上。然而,由于只有优化变量中的控制参数出现在目标函数中,信任域只需要设定在所有控制参数当前点的周围即可,如(21)式所示。

(20)

(21)

3多无人机编队建立的优化算法

至此,基于控制向量参数化方法和SCP技术,可以构建求解能量最优控制问题的算法,如算法1所示。在算法1中,步骤2利用控制参数化方法,而步骤3采用了SCP方法。在SCP方法中,优化变量{ξk}k≥1一直迭代直到满足预先设定的收敛条件ε>0为止。在该算法中,可运用开源软件CVX求解问题(20)[12],同时也可以求得相对于最终队形约束的拉格朗日算子。一旦计算得到能量最优控制向量,对(10)式积分即可得到建立编队的飞行轨迹。

算法1求解能量最优控制问题的SCP算法

1:迭代开始

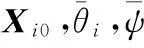
3:运用CVX求解问题(20),得到ξk的一个解。

4:k=k+1。

5:直到‖ξk-ξk-1‖≤ε时迭代结束。

输出:ξ

4V型编队建立的仿真算例

在本节中,将提出的算法运用到3个无人机的V型编队建立中,并且将仿真结果与运用Matlab中全局优化方法得到的结果进行比较,其中,该全局优化方法采用了多个起始点。首先,假设3个无人机当前分别以200 m/s、100 m/s和100 m/s的速度飞行,它们的初始状态如下所示

假设上面的这3个无人机需要在50 s内建立1个V型编队。在最终编队队形中,编队建立将要到达的位置和编队建立时的飞行攻角以及方向角一起被定义为参考参数。对于V型编队,这3个无人机的最终状态与参考参数之间的差值设置如下

在本文的仿真中,将时间区间划分为60个相等的子区间。在算法实现中,并没有设定停止准则来结束该仿真;相反,只限制了迭代次数(例如,进行50次迭代)。对于每一次迭代,它的最优控制问题都使用免费开源软件CVX进行求解。当仿真结果收敛时,编队建立过程中消耗的总能量是0.254 6,计算得到的参考参数及各个无人机的最终状态为

图1显示了总能量消耗随着迭代次数收敛的曲线。图2显示编队建立过程中,所有无人机的三维轨迹,而图3显示了X-Y平面内的二维轨迹。

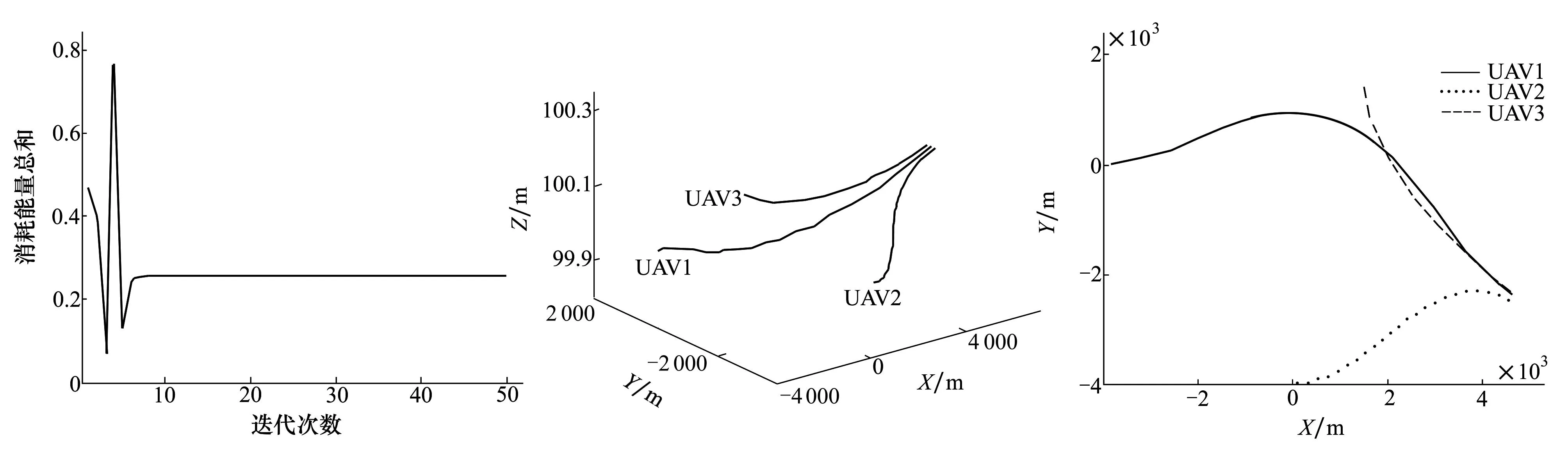
图1　V型编队建立过程中的总能量消耗　图2　V型编队建立的3-D轨迹　图3　X-Y平面内V型编队建立的2-D轨迹

因为状态约束和最终编队队形约束的梯度方程可以视为已知,所以也可以采用SQP和内点法来求解能量最优的编队建立问题。在研究中,内点法直接通过Matlab提供的fmincon函数实现。如果将之前的仿真设置再次用到内点法中,将会得到与运用SCP法相似的结果。然而,内点法需要进行67次迭代才能收敛,而本文提出的方法仅需11次迭代就可收敛,如图1所示。另外,除了将SCP法与上述局部优化方法进行比较,本文还采用多个初始点的全局优化技术来寻找全局最小值。具体采用的是Matlab中的MultiStart求解器,它利用随机分布的初始点寻找多个局部最小值。对于上述能量最优的编队建立算例,在优化变量ξ允许的范围内,总共产生了20个随机初始点。对于每个初始点,MultiStart求解器采用内点法求解相应的优化问题。最终计算结果表明,能量消耗0.254 6是全局最小值。

5结论

本文提出了一个简单高效的算法可实现多无人机能量最优的编队建立。该方法利用了控制向量参数化方法以及迭代凸规划技术的优点,且可以基于一个免费开源的凸优化求解器进行算法的实现。该方法可应用于存在非线性动力学约束和非凸局部约束和/或耦合约束的编队建立问题。本方法在直接法的基础上先将最优控制问题近似为非线性规划问题,再进一步使用迭代凸规划技术(SCP)将其近似为一系列凸规划问题。SCP迭代的每一步本质上是一个受线性约束的二次型规划问题,可以高效地进行求解。与Matlab中提供的全局优化技术相比,采用本文算法能够非常迅速地收敛到全局最小值。

参考文献：

[1]Burkle A, Segor F, Kollmann M. Towards Autonomous Micro UAV Swarms[J]. Journal of Intelligent Robotic Systems, 2011, 61(1): 339-353

[2]Navaravong L, Kan Z, Shea J M, et al. Formation Reconfiguration for Mobile Robots with Network Connectivity Constraints[J]. IEEE Trans on Network, 2012, 26(4): 18-24

[3]Raffard R L, Tomlin C L, Boyd S P. Distributed Optimization for Cooperative Agents: Application to Formation Flight[C]∥Proceedings of 43rd IEEE Conference on Decision and Control, 2004: 2453-2459

[4]Betts J T. Survey of Numerical Methods for Trajectory Optimization[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 193-207

[5]Conway B A. A Survey of Methods Available for the Numerical Optimization of Continuous Dynamic Systems[J]. Journal of Optimization Theory and Applications, 2012, 152(2): 271-306

[6]Teo K L, Goh C, Wong K. A Unified Computational Approach to Optimal Control Problems[M]. Longman Scientific and Technology, Essex, 1991

[7]Boyd S, Vandenberghe L. Convex Optimization[M]. Cambridge University Press, New York, 2009

[8]Mattingley J, Boyd S. Cvxgen: a Code Generator for Embedded Convex Optimization[J]. Optimization and Engineering, 2012, 13(1): 1-27

[9]Bai R, Sun X, Chen Q, et al. Multiple UAV Cooperative Trajectory Planning Based on Gauss Pseudospectral Method[J]. Journal of Astronautics, 2014, 35(9): 1022-1029

[10] Chachuat B. Nonlinear and Dynamic Optimization: from Theory to Practice[R]. Technical Report, 2007

[11] Rao A V. A Survey of Numerical Methods for Optimal Control[J]. Advances in the Astronautical Sciences, 2009, 135(1): 497-528

[12] Grant M, Boyd S. Graph Implementations for Nonsmooth Convex Programs[M]. Springer, Berlin, 2008, 95-110

Establishment of UAV Formation Flight Using Control Vector Parameterization and Sequential Convex Programming

Guo Juan1, Chu Jing2, Yan Jie1

1.School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.School of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China

Abstract:Formation flight of multiple Unmanned Aerial Vehicles (UAVs) could provide an effective, efficient yet cost reduction alternative to existing technologies of various applications. This paper addresses the energy-optimal establishment of UAV formation flight that shall satisfy final configuration constraints. First, the problem of formation establishment is formulated as an energy-optimal control problem which is subject to the nonlinear dynamics constraints. Then, the optimal control problem is solved using a direct method. In this direct method the original problem is transcribed into a sequence of convex optimization problems via the control vector parameterization approach. After that, the sequential convex programming (SCP) technology is employed to derive the optimal solution. Essentially, each instance of SCP is a quadratic programming problem subject to linear constraints that can be solved very efficiently. In the end, the proposed method is applied to the establishment of V formation for three UAVs, where the free open source CVX is exploited. By comparison with the global optimization technique provided in MATLAB, the solution converges very fast to the global minimum.

Keywords:convex optimization, cost reduction, MATLAB, parameterization, unmanned aerial vehicles(UAVs), formation flight, optimal control, control vector parameterization, sequential convex programming

收稿日期：2016-03-25

作者简介：过娟(1986—)，女，西北工业大学博士研究生，主要从事分布式优化及制导技术的研究。

中图分类号：TP391

文献标志码：A

文章编号:1000-2758(2016)04-0607-07