机动目标的IMM扩展卡尔曼滤波时间配准算法
高颖, 韩宏帅, 武梦洁, 王永庭
(1.西北工业大学 航海学院, 陕西 西安 710072; 2.光电控制技术重点实验室, 河南 洛阳 471009)
机动目标的IMM扩展卡尔曼滤波时间配准算法
高颖1,2, 韩宏帅1, 武梦洁2, 王永庭2
(1.西北工业大学 航海学院, 陕西 西安710072; 2.光电控制技术重点实验室, 河南 洛阳471009)
摘要:针对目前研究的时间配准方法是在目标运动模型已知的情况下进行时间配准,难以保证目标在复杂机动情况下运动模型多变时的时间配准精度。提出了机动目标的交互多模型扩展卡尔曼滤波(IMM-EKF)时间配准算法,该算法将交互多模型中的每个运动模型分别进行扩展卡尔曼滤波输出同时根据滤波过程中得到的残差计算每个模型的概率,根据模型概率和各模型滤波输出得到时间配准周期内最后一个采样点的测量数据,利用该点的状态和模型概率进行外推就得到时间配准周期和传感器采样周期不成整数比时配准时刻的位置。通过仿真结果表明该算法能够有效降低整体的时间配准误差。该算法提高了时间配准的精度,为数据融合提供了良好的基础。
关键词:信息融合;交互多模型;扩展卡尔曼滤波;时间配准
在多传感器信息融合系统中,综合使用多个传感器的观测值,能够更加有效地对目标的位置和速度信息进行精确估计[1]。由于传感器的采样频率、传感器测量误差、采样起始时间的不同以及数据链传输数据的时延不同,所以在进行融合处理前必须将这些数据同步到相同的时刻上,即进行时间配准。时间配准过程就是在已有数据基础上产生配准时刻的数据。若融合时直接使用未经过时间配准的数据进行融合,可能会导致融合输出的结果比单独使用某一传感器的数据还要差,因此,在多传感器信息融合处理前必须考虑时间配准问题[2],对多传感器探测数据进行时间配准处理精度直接关系到信息融合的最终效果。
目前常用的时间配准方法主要包括内插外推法、滤波方法、曲线拟合法、最小二乘法等,各算法都有其优缺点。文献[3]中的内插外推法是一种较常用的方法,采用三点插值法或拉格朗日插值法,将配准时刻定为插值点,从而得到配准时刻的数据,实现时间配准,但是根据插值法的算法原理,为了保证较高的插值精度,插值数据应处在插值区间中部,因此该算法用于事后处理效果较好,但无法满足机动目标配准的精确性要求。在解决时间配准问题时,滤波的方法也被应用时间配准中,其中文献[4]采用EKF算法对目标进行精确时间配准是一种较好的时间配准方法,但是该算法的滤波过程是在假设目标运动模型为匀速直线运动模型、匀加速直线运动和匀速圆周运动单个运动模型的基础之上进行准确时间配准的,但是实际机动目标的运动模型未知且是复杂多变的,若运动模型失配,则该滤波算法的配准精度急剧下降;文献[5]采用UKF算法同时对时间和空间进行配准,该方法不失为一次较好的尝试,但其推导过程是基于目标匀速运动的假设,也是在模型已知的基础上进行时间配准,若运动模型失配,则时间配准精度降低。文献[6-7]中曲线拟合算法根据一段区间内的采样数据,由最小二乘准则拟合出一条以时间为变量的多项式曲线,从而得到配准时刻的数据,实现时间配准,但是当配准时刻在拟合曲线的端点处时存在发散现象,导致时间配准的精度在端点处急剧下降,而且该算法同样无法解决时间配准的准确性问题。文献[8]对曲线拟合的方法进行了改进,提出了自适应变长滑窗曲线拟合时间配准算法,该算法在大时延、目标大机动条件下仍然具有较好的可靠性,但是若传感器的数据采样周期和时间配准周期相差不大时,就无法采用该算法进行时间配准,因此限制了此算法的应用范围。文献[9]提出了多模型最小二乘算法,该算法解决了时间配准周期与传感器采样周期比为非整数这一问题,但是该算法也是在运动模型已知的情况下进行外推得到配准时刻的值,不适用于机动或复杂运动模型时的时间配准精度。文献[10]提出了基于机动检测的自适应时间配准算法,由于数据存在滤波误差,自适应算法的门限判断并不能保证完全准确切换为目标当前的运动模型,此外目标机动时滤波结果与真实值相比存在一定的滞后性,再加上自适应算法需要对两点数据进行差分以计算目标的加速度,这都给该配准算法的实时切换带来影响,进而影响时间配准的准确性。在机动目标的跟踪中,交互多模型等机动跟踪算法[11],实现对机动目标的稳定跟踪,文献[12-13]把交互多模型运用到机动跟踪算法中,由于使用了交互多模型算法,机动目标的跟踪精度有了较大提高,这主要是因为交互多模型算法对机动目标运动模型的精确估计,所以利用交互多模型的方法来解决时间配准过程中模型失配的问题。
针对机动目标时间配准中的运动模型失配导致配准精度降低的问题,根据交互多模型算法对机动目标运动模型的准确估计和扩展卡尔曼滤波在时间配准上可滤除由于雷达传感器引入的随机噪声,在交互多模型算法和扩展卡尔曼滤波算法的基础上提出了交互多模型扩展卡尔曼滤波时间配准算法,该算法中由多个运动模型组成,通过对多个运动模型进行滤波并根据模型概率将这些滤波结果融合输出,得到距配准时刻最近采样点的滤波输出,然后根据该点状态和该点到配准时刻的时间间隔外推求解时间配准周期和传感器采样周期不成整数比时时间配准时刻的位置。
1基于IMM-EKF的时间配准算法
1.1整数周期比条件下IMM-EKF时间配准
交互式多模型算法利用模型的转移和多个模型的组合对机动目标的状态进行估计,通过选取或设计一个模型集来描述目标系统的行为模式,其中每个模型与系统的一个特定模式相匹配;然后基于每一个模型的滤波器并行滤波,通过EKF滤除测量过程中的随机误差以此来提高测量数据的精度,利用每个滤波器输出的残差以及各模型的先验概率密度,得出当前时刻与模型匹配的模型概率,系统最终的测量数据就是各模型滤波器输出的概率加权融合。算法流程如图1所示。
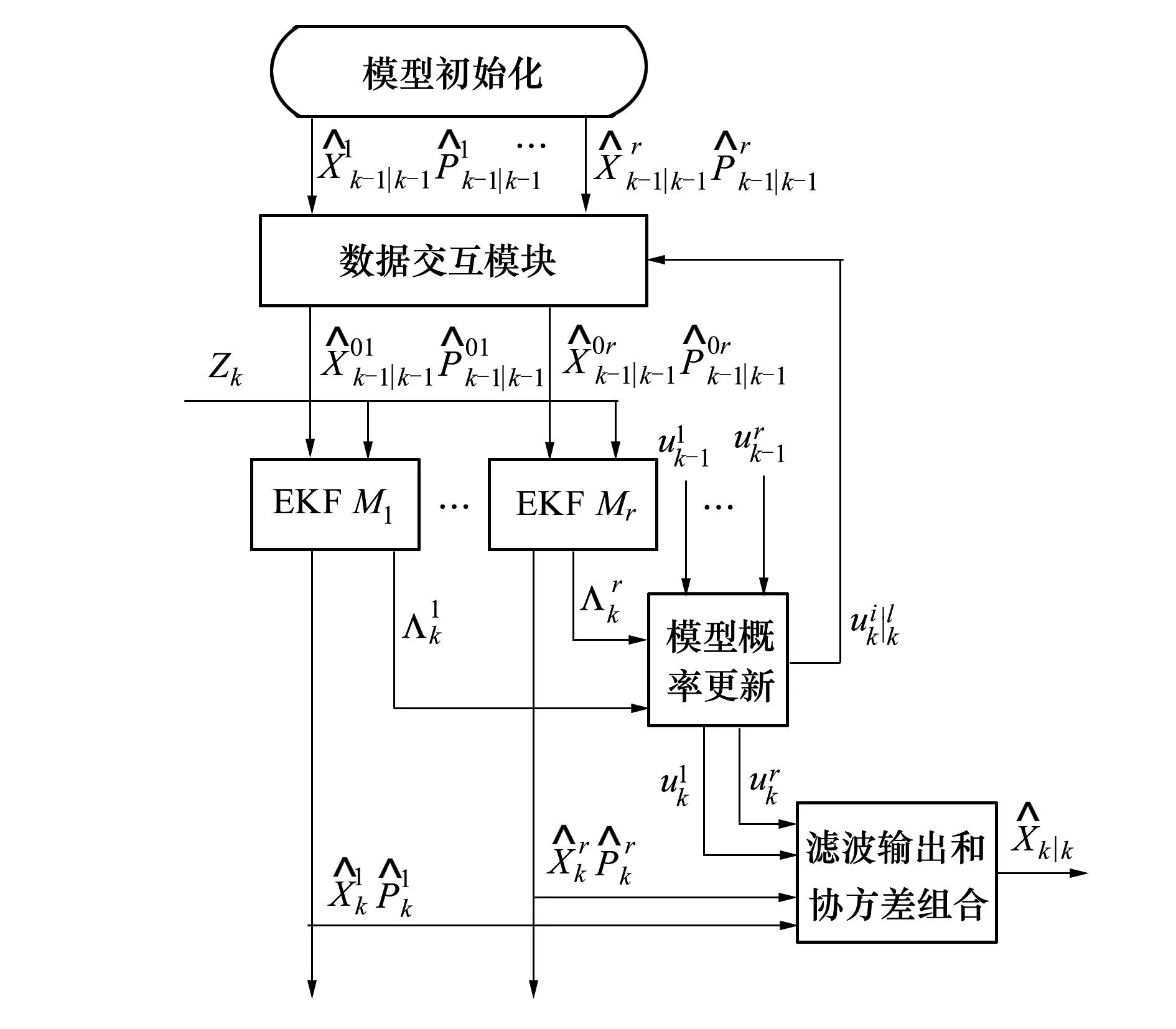
图1 交互多模型算法流程
该算法假设配准周期为T,传感器的采样周期为τ,配准周期与传感器的采样周期成整数比,所以T=nτ。
假定有r个模型
(1)
式中,Fi是由运动模型而确定的状态转移矩阵,wi(k)是均值为零、协方差矩阵为Q的白噪声序列。
测量模型为
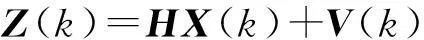
(2)
由图1可知,IMM-EKF算法主要包括四个步骤:①输入交互;②各模型扩展卡尔曼滤波;③模型概率更新;④交互输出。具体内容如下:
1) 输入交互
(3)
(4)
(5)
(6)
2) 各模型扩展卡尔曼滤波
根据输入交互及k时刻的量测数据Zk,对各个模型进行扩展卡尔曼滤波。
预测:
(7)
卡尔曼滤波增益
(8)
状态估计更新
(9)
状态协方差阵更新
(10)
(11)
(12)
3) 模型概率更新
模型概率更新方程为
(13)
(14)
(15)
4) 交互输出
(16)
1.2非整数周期比条件下IMM-EKF时间配准
若配准周期与传感器的采样周期比不是整数倍时,即T=nτ+ε,其中,n是一个配准周期内的n个采样点,ε为一个配准周期内最后一个采样点到配准时刻的时间间隔。其具体情形如图2所示。
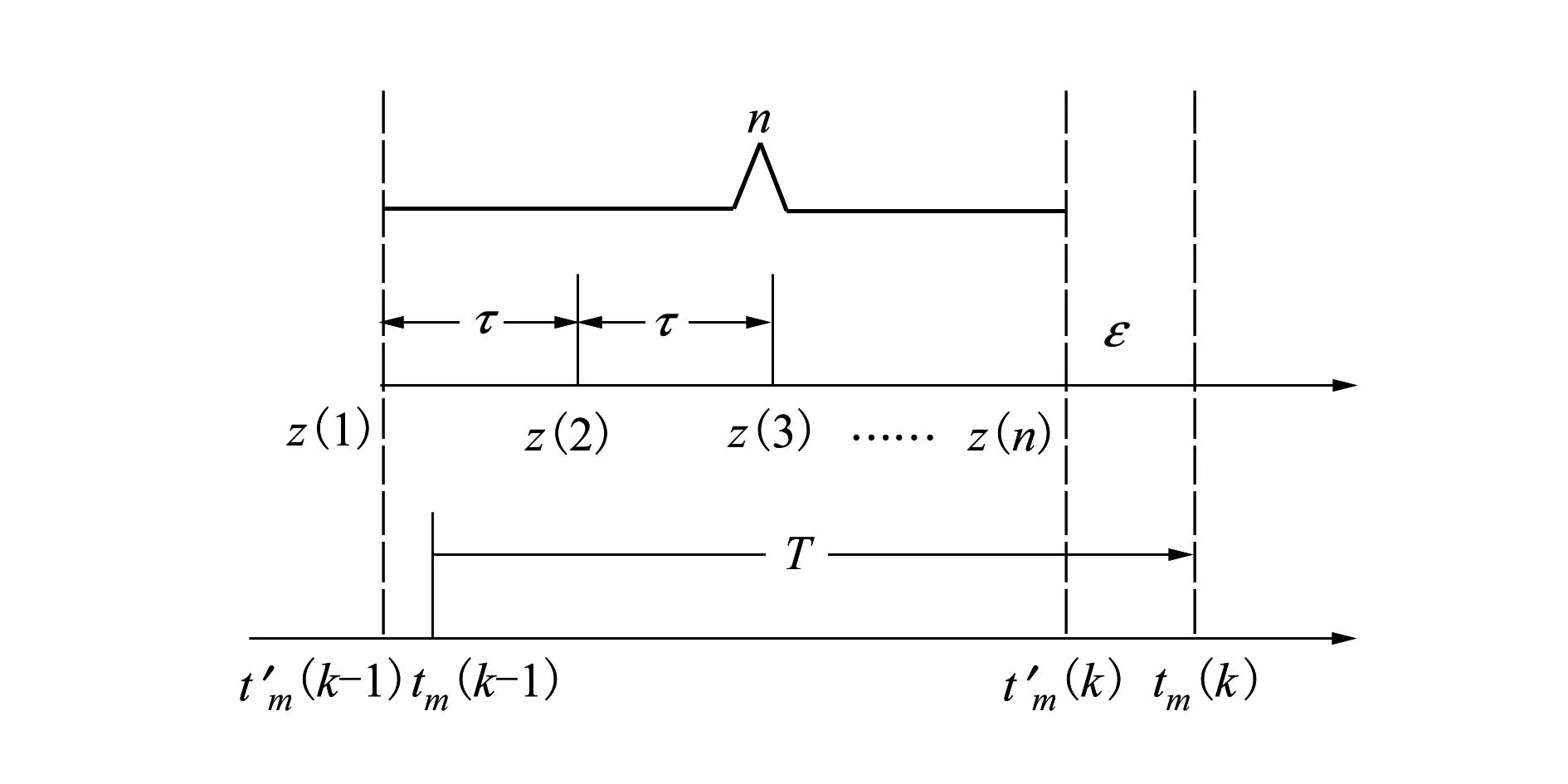
图2 非整数周期比条件下IMM-EKF时间配准
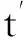
(17)
(18)
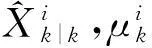
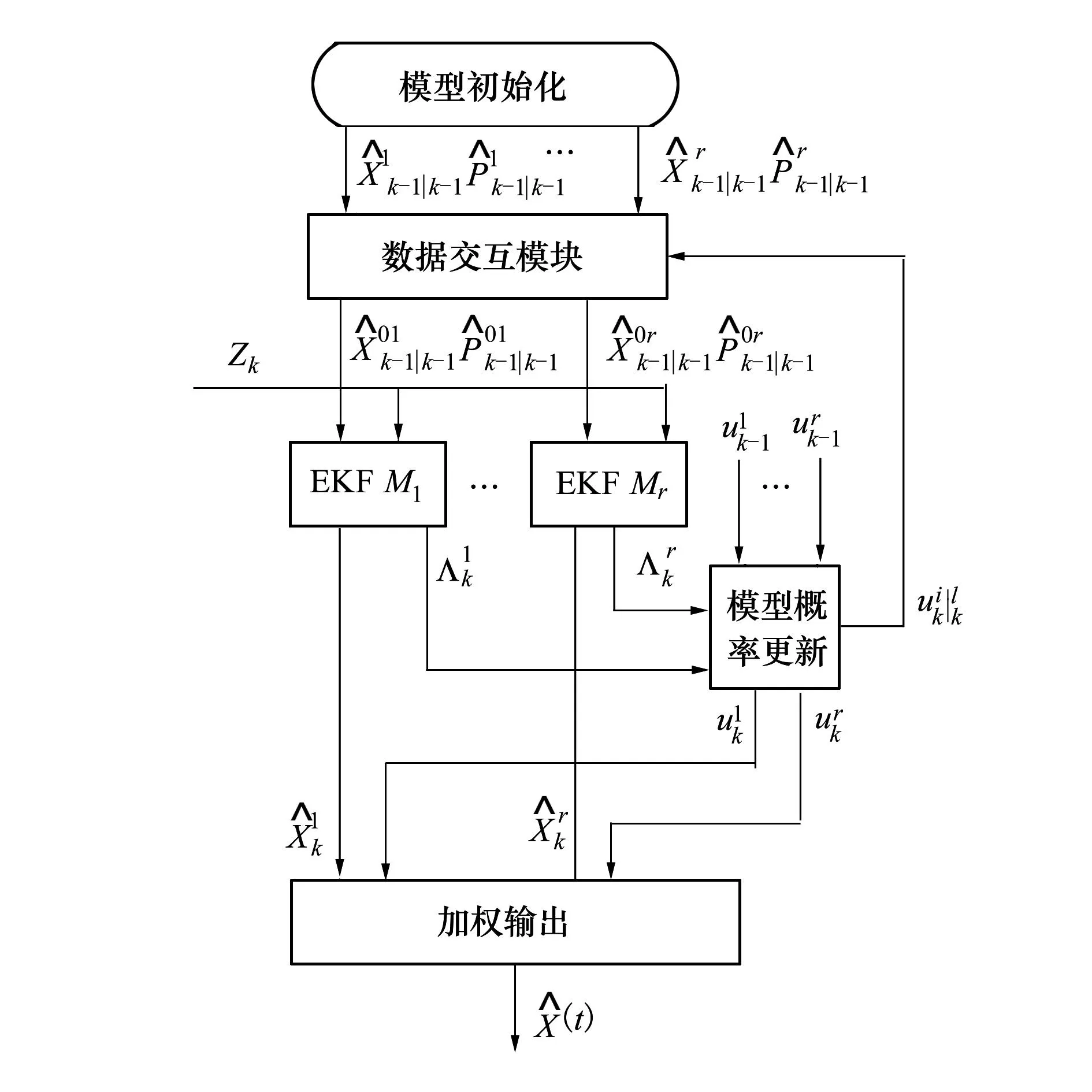
图3 非整数周期比条件下配准算法流程
2仿真结果和分析
为了验证本文所述算法的有效性,将该IMM-EKF算法和匀速(CA)、匀加速(CV)模型下的EKF算法进行了一组仿真对比实验, IMM-EKF算法中的模型为匀速和匀加速运动模型。仿真实验假设目标在X-Y平面上做蛇形机动,初始位置为(200m,150m),仿真时间设为100s,机动目标的实际运动轨迹如图4所示。
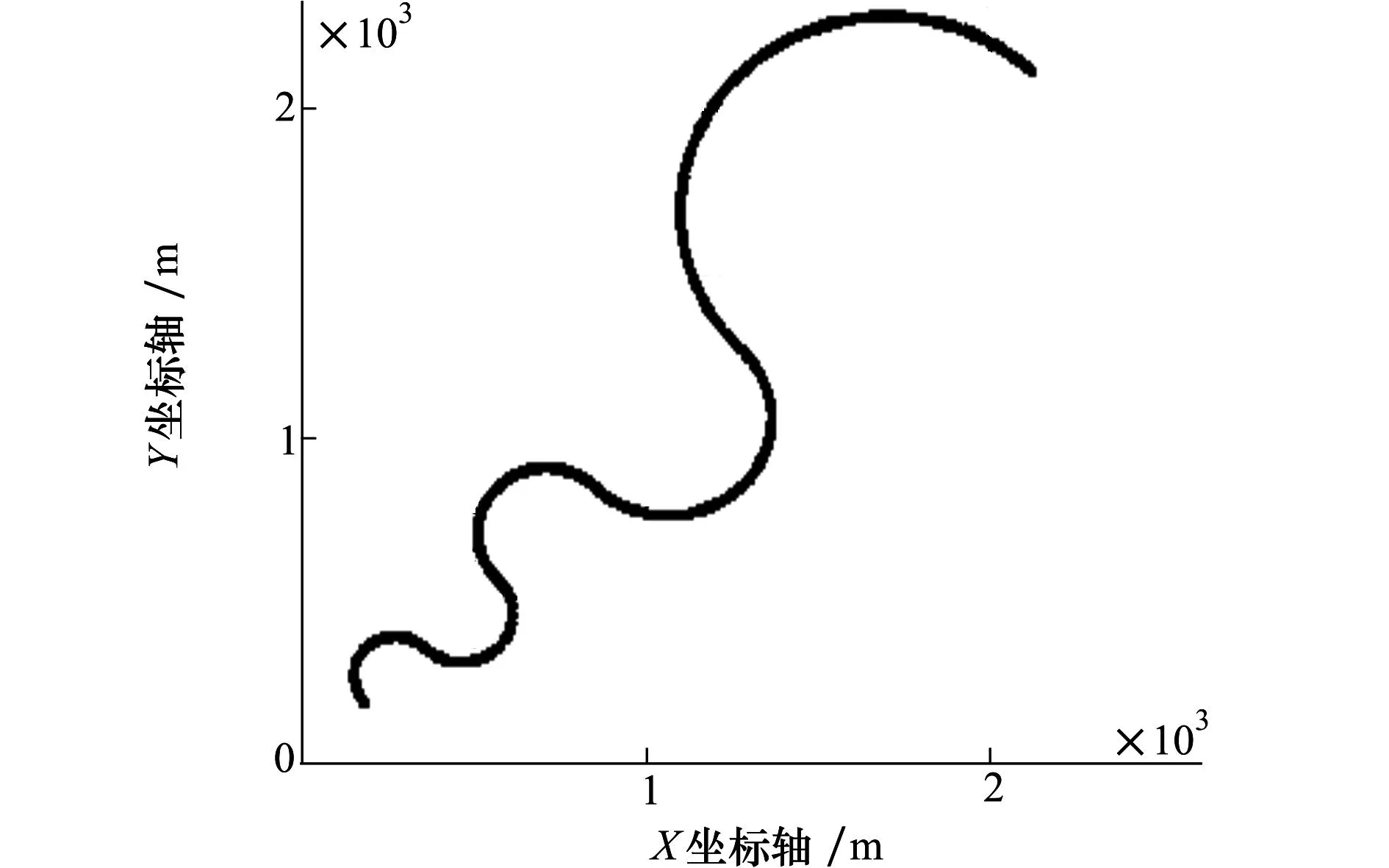
图4 机动目标的运动轨迹
雷达的测距误差为30m。假设雷达传感器位于坐标原点,其中在交互多模型中,多模型由匀速(CA)、匀加速(CV)2个运动模型组成,这2个模型在IMM-EKF中对应的状态转移矩阵F1、F2为:
(19)
(20)
在仿真实验中,蒙特卡洛仿真次数M为50次,以位置估计均方根误差(RMSE)作为目标跟踪性能的比较依据,表达式如下
(21)
(22)
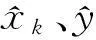
1) 雷达传感器采样周期与时间配准周期成整数比时,当雷达传感器的采样周期为0.15s,时间配准周期为0.9s时,CV、CA模型和IMM3种情况下的时间配准仿真实验结果如图4所示,在配准时刻位置估计的均方根误差均值如表1所示。
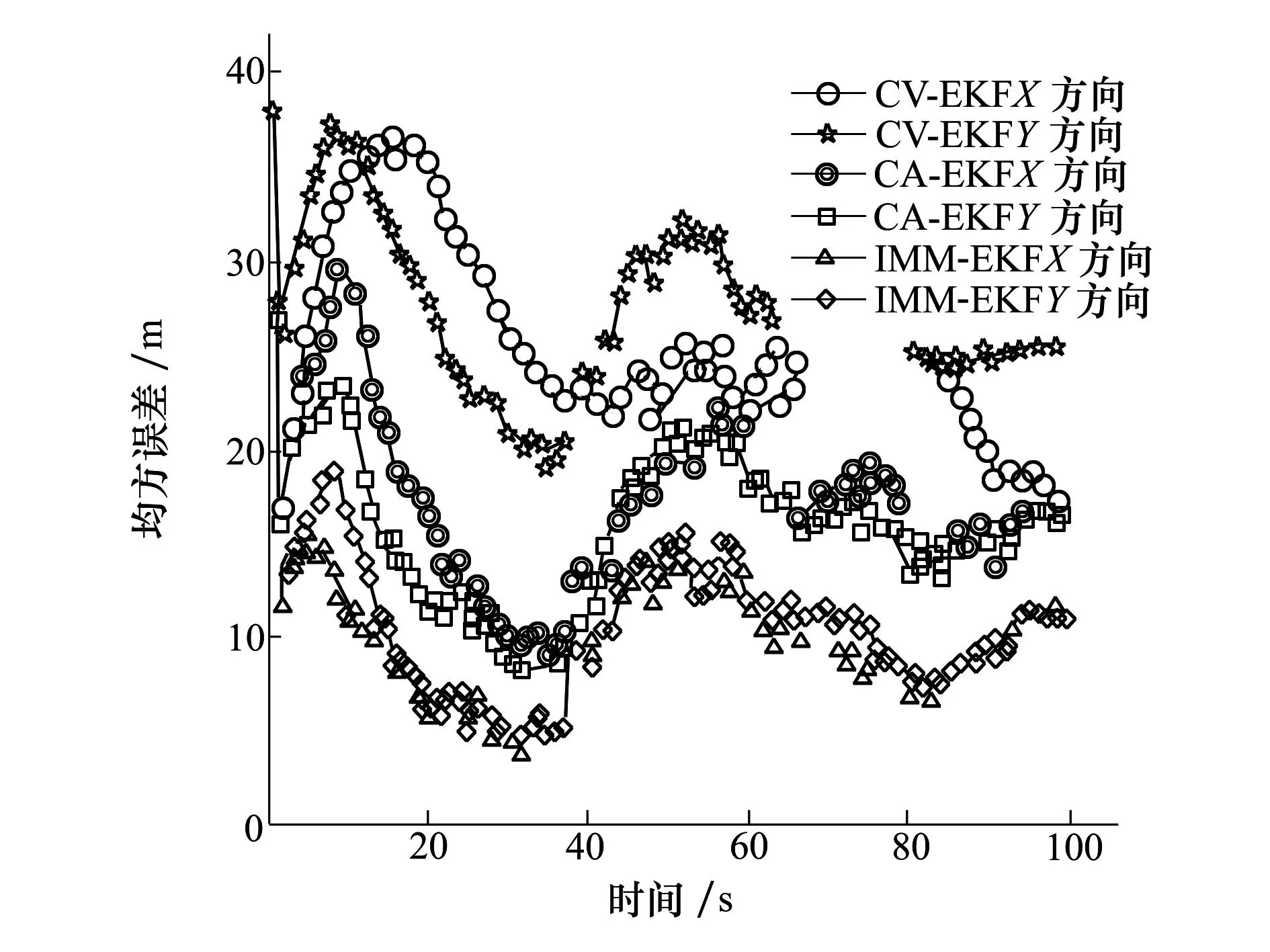
图5 时间配准算法性能比较
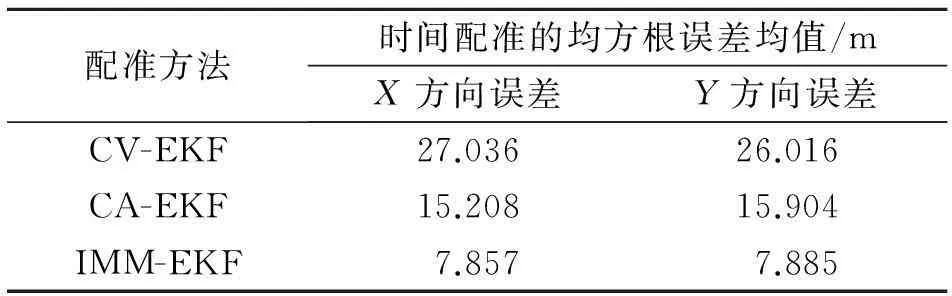
配准方法时间配准的均方根误差均值/mX方向误差Y方向误差CV-EKF27.03626.016CA-EKF15.20815.904IMM-EKF7.8577.885
由图5和表1当雷达传感器的采样周期和时间配准周期成整数比,IMM-EKF时间配准算法明显优于单个CV、CA模型的时间配准精度,表明IMM-EKF时间配准算法的时间配准精度优于单模型下的时间配准精度。
2) 雷达传感器采样周期与时间配准周期不成整数比时,以上仿真参数不变,雷达传感器的采样周期为0.15 s,时间配准周期为1 s时,CV、CA模型和IMM 3种情况下的时间配准仿真实验结果如图6所示,在配准时刻位置估计的均方根误差均值如表2所示。
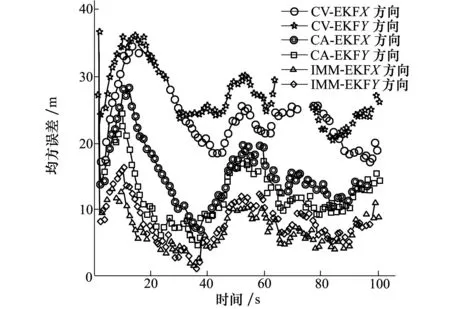
图6 时间配准算法性能比较
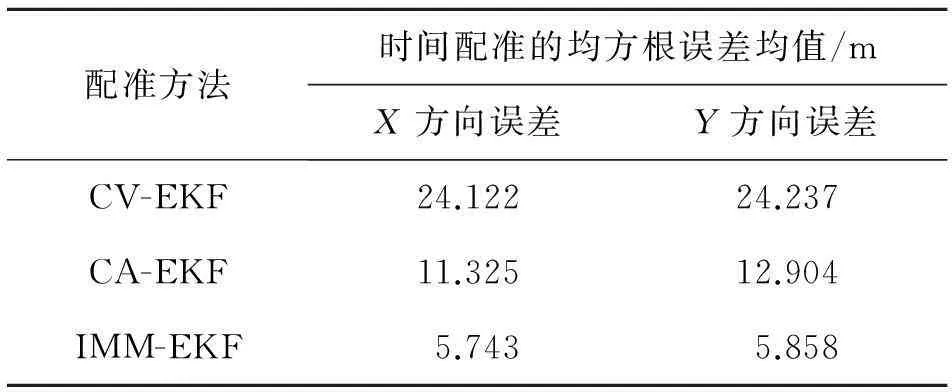
配准方法时间配准的均方根误差均值/mX方向误差Y方向误差CV-EKF24.12224.237CA-EKF11.32512.904IMM-EKF5.7435.858
从图6及表2中的仿真结果可以看出:IMM-EKF的时间配准精度优于单个CV、CA模型下的EKF时间配准精度。单个CV、CA模型下的EKF时间配准算法在对机动目标进行时间配准是由于运动模型失配,导致配准误差逐增大,所以单个运动模型下的EKF时间配准算法无法保证目标在复杂机动条件时间配准的精度。而IMM-EKF时间配准算法由于其利用了交互多模型算法,将每个模型与对应的滤波器进行滤波输出并根据残差计算每个模型的概率从而能够精确估计距配准时刻最近采样点的状态,然后就能正确外推出配准时刻的位置,从而提高了时间配准算法的精度。
3结论
针对传统时间配准算法在运动模型失配时配准精度下降问题,将交互多模型(IMM)算法和扩展卡尔曼滤波相结合,提出了交互多模型扩展卡尔曼滤波(IMM-EKF)时间配准算法,通过仿真验证该算法明显优于传统单模型的扩展卡尔曼滤波(EKF),解决了机动目标时间配准过程中的模型失配问题。另外,将单模型扩展卡尔曼滤波扩展到多模型,解决了复杂机动目标的时间配准问题,提高时间配准的精度。所以该算法能够根据传感器的观测值精确估计机动目标在配准时刻运动的位置,具有广泛的实用价值。
参考文献:
[1]胡国平,张守宏. 多传感器协同探测目标的分类识别研究[J]. 西安电子科技大学学报,2009,36(3):443-447
Hu Guoping, Zhang Shouhong. Study of Target Recognition Based on Multi-Sensor Cooperating with Exploration[J]. Journal of Xidian University, 2009, 36(3): 443-447 (in Chinese)
[2]Hernandez M, Benavoli A, Graziano A, et al. Performance Measures and MHT for Tracking Move-Stop-Move Targets with MTI Sensors[J]. IEEE Trans on Aerospace and Electronic Systems, 2011, 47(2): 996-1025
[3]王宝树, 李芳社. 基于数据融合技术的多目标跟踪算法研究[J]. 西安电子科技大学学报,1998,25(3): 269-272
Wang Baoshu, Li Fangshe. Multi Target Tracking Algorithm Base on Data Fusion[J]. Journal of Xidian University,1998, 25(3): 269-272 (in Chinese)
[4]施立涛. 多传感器信息融合中的时间配准技术研究[D]. 长沙: 国防科技大学,2010
Shi Litao. Study on Time Registration Technology for Multi-Sensor Information Fusion[D]. Changsha, National University of Defense Technology, 2010 (in Chinese)
[5]Li W, Leung H, Zhou Yifeng. Space-Time Registration of Radar and ESM Using Unscented Kalman Filter[J]. IEEE Trans on Aerospace and Electronic System, 2004, 40(3): 824-836
[6]潘自凯,董文锋,王正国. 基于曲线拟合的PRS/IRS时间对准方法研究[J]. 空军雷达学院学报,2011,25(5): 343-346
Pan Zikai, Dong Wenfeng, Wang Zhengguo. Study on PRS/IRS Time Registration Based on Curve Fitting[J]. Journal of Air Force Radar Academy, 2011, 25(5): 343-346 (in Chinese)
[7]梁凯, 潘泉, 宋国民,等. 基于曲线拟合的多传感器时间对准方法研究[J]. 火力与指挥控制, 2006,31(12): 51-53
Liang Kai, Pan Quan, Song Guoming, et al. The Study of Multi-Sensor Time Registration Method Based on Curve Fitting[J]. Fire Control and Command Control, 2006, 31(12): 51-53 (in Chinese)
[8]雍霄驹,方洋旺,高翔,杨鹏飞. 自适应变长滑窗曲线拟合时间配准算法[J]. 西安电子科技大学学报, 2014, 41(3): 209-213
Yong Xiaoju, Fang Yangwang, Gao Xiang, Yang Pengfei. Time Registration Using the Curve Fitting Algorithm of the Adaptive Changed Length Moving Window[J]. Journal of Xidian University, 2014, 41(3): 209-213 (in Chinese)
[9]雍霄驹,方洋旺,高翔,张磊,封普文. 用于多源信息中制导的MM-LS时间配准算法[J]. 西安电子科技大学学报,2014,41(4):166-172
Yong Xiaoju, Fang Yangwang, Gao Xiang, Zhang Lei, Feng Puwen. MM-LS Time Registration Algorithm in Middle Guidance Using Multi-sensor Information[J]. Journal of Xidian University, 2014, 41(4): 166-172 (in Chinese)
[10] 董凯,关欣,刘瑜,何友. 基于机动检测的自适应实时时间配准算法[J]. 雷达科学与技术,2014,12(2):86-90
Dong Kai, Guan Xin, Liu Yu, He You. Adaptive Real-Time Registration Algorithm Based on Target Maneuver Detection[J]. Radar Science and Technology, 2014, 12(2): 86-90 (in Chinese)
[11] Chang Dahchung, Fang Mengwei. Bearing-Only Maneuvering Mobile Tracking With Nonlinear Filtering Algorithms in Wireless Sensor Networks[J]. IEEE Trans on Systems Journal, 2014, 8(1): 160-170
[12] 李世忠,王国宏,吴巍,苏少涛. 雷达间歇工作下的雷达/红外复合制导跟踪[J]. 红外与激光工程,2012,41(6): 1405-1410
Li Guozhong, Wang Guohong, Wu Wei, Su Shaotao. Radar and Infaraed Sensor Compound Guidance with Radar Under Intermittent-Working State[J]. Infrared and Laser Engineering, 2012, 41(6): 1405-1410 (in Chinese)
[13] 张俊根,姬红兵. IMM迭代扩展卡尔曼粒子滤波跟踪算法[J]. 电子与信息学报,2010,32(5):1116-1120
Zhang Jungen, Ji Hongbing. IMM Iterated Extended Kalman Particle Filter Based Target Tracking[J]. Journal of Electronics & Information Technology, 2010, 32(5): 1116-1120 (in Chinese)
IMM Extended Kalman Filter Time Registration Algorithm Based on Maneuvering Target
Gao Ying1,2, Han Hongshuai1, Wu Mengjie2, Wang Yongting2
1.School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China 2.Science and Technology on Electro-Optic Control Laboratory, Luoyang 471009, China
Abstract:Now time registration process is researched at the situation of the target model known. In fact, it is difficult to make ensure accuracy of the time registration when sports model of the maneuvering target are always varied and not known previously. This paper presents an algorithm on IMM extended Kalman filter (IMM-EKF) time registration based on maneuvering target. In the algorithm, each motion model were output by extended kalman filter while residues obtain by the filtering process differential probability to calculate for each model, and use the model probability and output of each model to calculate last sample point state estimation, then use the point of state and probabilistic models to extrapolate to obtain the registration time position when ratio between the period of time registration and the period sensor sampling is not an integer. The simulation results show that the algorithm can effectively reduce the overall time of registration error. The algorithm improves the accuracy of the registration period for data fusion provides a good foundation.
Keywords:data fusion, extended Kalman filters, information fusion, IMM, EKF, time registration
收稿日期:2016-03-03
基金项目:光电控制技术重点实验室与航空科学基金(20145153027)资助
作者简介:高颖(1965—),西北工业大学副教授,主要从事虚拟现实及数据融合研究。
中图分类号:TN95.3
文献标志码:A
文章编号:1000-2758(2016)04-0621-06

