新型机翼后缘变弯运动机构仿真及其气动影响研究

沈广琛, 白俊强, 刘南, 刘睿

(西北工业大学 航空学院, 陕西 西安　710072)



新型机翼后缘变弯运动机构仿真及其气动影响研究

沈广琛, 白俊强, 刘南, 刘睿

(西北工业大学 航空学院, 陕西 西安710072)

摘要：采用计算流体力学方法和CATIA DMU Kinematics机构仿真,对一套可用于目前及未来民用客机机翼后缘变弯的增升装置系统进行研究,主要包括襟翼运动机构和扰流板下偏。通过运动学分析,采用的襟翼机构可保证巡航阶段后缘变弯过程中机构上下表面无缝,同时满足起降过程对襟翼的运动轨迹的要求。相比简单铰链机构,应用该机构的起飞构型线性段升力系数增加0.05,升阻比的增加量在0.2%～3%范围内;着陆阶段扰流板下偏,较未偏转扰流板的最大升力系数增加1.14%,且线性段上移0.15,显示了该机构具有较高的增升效率。在二维翼型上应用该机构实现后缘变弯度,升阻比有较大提升,且根据来流马赫数的不同改变后缘弯度可以有效地提高阻力发散马赫数。在某远程宽体客机翼身组合体构型上应用该机构实现巡航阶段后缘变弯度,巡航升阻比的增加量在0.345%～2.28%范围内。综上所述,在不增加机构复杂性和重量的前提下,研究的新型机翼后缘变弯运动机构能够有效地提高气动效率。

关键词：增升装置;空气动力学;机构;后缘变弯度;计算流体力学;气动构型;升阻比;马赫数

飞机的气动效率(L/D)是影响航空公司运营的一个重要因素。对于现代一些远程宽体客机,燃油费用接近航空公司运营费用的50%。每架飞机减少3%的燃油消耗,每年便可节约300 000美元[1]。如何降低巡航时的阻力以提高空气动力效率,进而降低油耗以提高经济性是目前及未来民用客机设计中面临的主要技术难题之一。

层流的研究和实现还面临着很多的困难[2]。在不同工况下,通过改变机翼不同展向位置的弯度以优化机翼的几何外形,为提高民机经济性提供了新思路。传统民用飞机的机翼设计多是针对某个固定巡航状态进行设计,综合考虑整个飞行任务剖面各个飞行状态。飞机在设计点具有较优的气动性能,即对应特定的高度、马赫数和飞机重量。通常情况下,在飞机的整个飞行任务剖面中,这些参数是连续变化的。飞机有很大一部分时间是远离设计点的,在非设计点机翼的气动性能仍有很大的提升空间。通过改变机翼不同展向位置的弯度以优化机翼不同工况下的几何外形,可以保持较高升阻比,从而提高气动效率,降低燃油消耗。波音公司在1980年首先完成了机翼变弯度在运输类飞机上应用的评估。通过风洞试验及理论计算,论证了机翼变弯度在民用飞机上应用的可行性。其研究结果表明:变弯度构型显著提高了整个飞行剖面非设计点的气动性能。对于远程客机,可节约燃油3.1%以及减少2%的直接运营费用(DOC)[3]。同一时期,德国梅塞施密特-伯尔科-布洛姆(MBB)公司针对变弯度机翼也开展了大量研究工作,其研究工作构成了空客公司在A330/340机型上尝试变弯度基础设计工作的一部分[4]。随着材料科学的发展,基于智能材料的机翼连续变弯度成为近年来的研究热点[5],但距离工程实用还很遥远。目前所有的大型民用客机为了提高起降特性,都在前后缘分别安装了缝翼(或克鲁格襟翼、前缘下垂)和襟翼,而增升装置系统在巡航等除起降外的其他任务阶段并没有进行任何操纵。在巡航过程中通过偏转增升装置以优化机翼不同工况下的弯度,可减小巡航阻力,提高气动效率,在工程上也最易于实现。2006年,波音公司对外宣布针对B787客机测试发展了后缘可变弯度系统(trailing edge variable camber system,下文简写为TEVC),飞机巡航时可减小阻力0.4counts,相当于减轻重量340～450 kg[6]。同年7月,空客公司公布了A350XWB的设计,采用了与B787类似的后缘变弯度系统。国内关于变弯度机翼的研究较少,且在近几年才兴起。研究内容多是在二维翼型基础上,采用先进智能材料等实现光滑连续变弯度[7-8],还难以在工程实践中应用。在我国大力发展宽体民用飞机的背景下,研究工程实用的变弯度实现方式显得极为重要。本文研究了一套可用于巡航机翼变弯度的增升装置机构。分析了该机构的运动学特性并评估了其増升装置效率。研究了应用该机构实现后缘变弯度的二维翼型的气动性能,以及某远程宽体客机翼身组合体巡航构型后缘变弯度在气动上所能产生的收益。

1气动分析方法

随着计算机技术的提高,计算流体力学(CFD)逐步成为飞机设计的重要手段。与试验方法相比较,CFD花费低、周期短、损耗小,且方便流场显示及分析。本文运用CFD方法进行研究,其中求解雷诺平均Navier-Stokes方程在机翼设计和多段翼型的设计中得到广泛应用,其控制方程为

(1)

式中，U是解向量,F、G、H是通量项,J代表源项(当体积力和体积流可忽略时等于零)[9]。空间离散格式为二阶迎风Roe格式,隐式时间推进采用近似因子分解,湍流模型为k-ωSST[10]。

选择典型的二维增升装置起飞构型L1T2作为计算对象以验证计算方法的可靠性。网格为多块结构网格,如图1a)所示,网格单元总数8.4×104。在Ma=0.197,Re=3.52×106状态下进行计算。图1b)、图1c)分别为计算的升力系数和阻力系数,计算结果与试验值吻合较好。

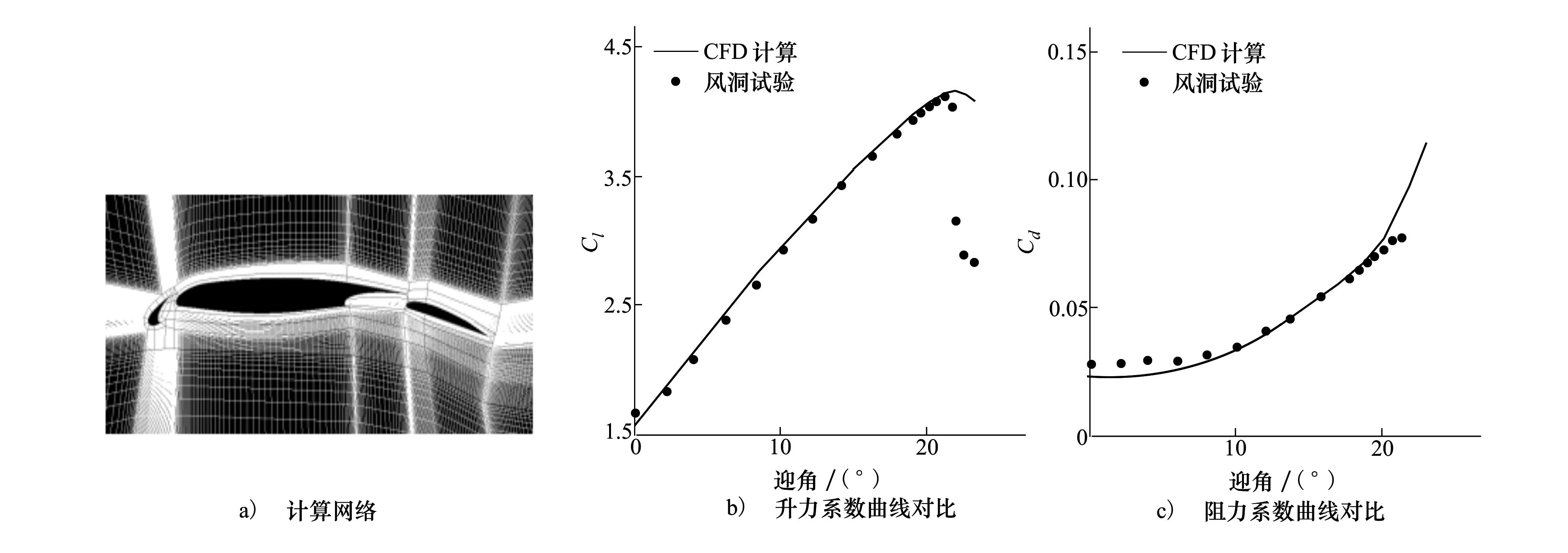
图1　L1T2网格及计算结果

为了更加全面地验证本文采用的气动分析方法的可靠性,采用半展长、无扭转角的后掠机翼ONERAM6机翼进行计算分析。计算状态为:M∞=0.839 5,Re=11.72×106(基于平均气动弦长0.646 07m),迎角α=3.06°。计算网格节点数为1 701 725,网格单元数为1 655 552。ONERAM6机翼计算网格如图2a)所示。图2b)为计算结果与试验结果对比,可以看出,本文计算方法准确捕捉到了压力峰值及激波位置。验证了气动分析方法的可靠性。

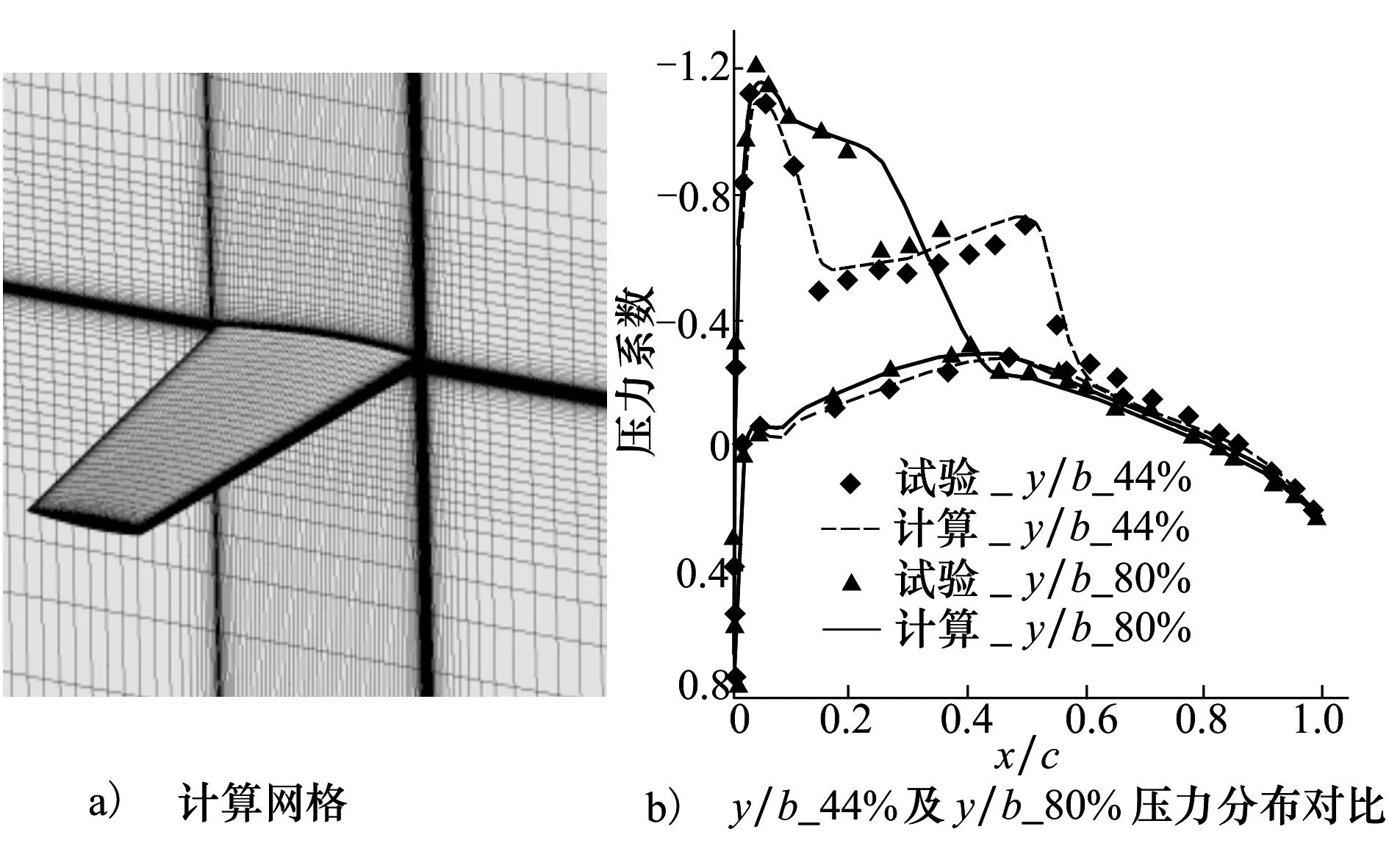
图2　ONERA M6网格及计算结果

2机构及运动学分析

由于襟翼占据了机翼后缘展长的大部分位置,故本文重在研究后缘襟翼机构。后缘襟翼机构与下偏扰流板协同作用构成了本文的后缘变弯系统。

2.1机构组成

以截取的某宽体飞机翼身组合体KINK位置处的翼型为研究对象进行机构设计,局部放大图如图3所示。襟翼弦长为21.78%C。在波音公司专利US2013/0075537Al[11]基础上,优化各构件杆长以及连接铰链的位置等,在保证良好的起飞着陆特性的同时,满足巡航阶段后缘变弯度的要求。

图3　机构侧视图

该机构属于连杆机构,如图4所示。

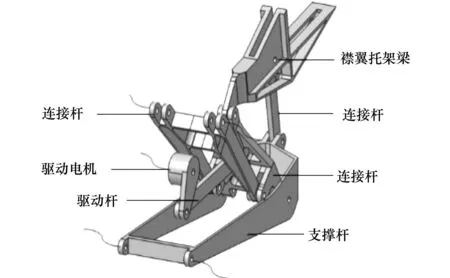
图4　机构组成

主要由7个构件组成:支撑梁(supportbeam)、襟翼托架梁(carrierbeam)、驱动电机(actuator)以及连接杆(AB杆、CD杆、connectionlink、drivelink),襟翼机构与可上下偏转扰流板组成后缘变弯度系统(TEVCsystem)。S形曲线处固定铰支在机翼结构上。驱动电机输入驱动力,通过各杆件传动使襟翼托架梁带动襟翼运动。巡航阶段,襟翼后缘向上向下最大可偏转1.5°,且每隔0.5°为一个档位。同时,扰流板下表面紧贴襟翼上表面,在变弯过程中随着襟翼的上下运动而运动,实现机翼表面连续无缝。起降阶段,襟翼向下最大可偏转37°。此时,通过调整扰流板位置可改变缝道参数,形成更有效的缝道射流,提高增升装置的效率。

2.2运动学分析

为了更好地分析机构的运动,通过CATIA软件的DMUKinematics模块,对巡航阶段机翼后缘襟翼变弯度以及起飞着陆阶段襟翼展开过程分别进行运动仿真。输出巡航及起飞着陆阶段襟翼运动轨迹进行运动学分析。

图5为变弯度时各档位所对应的襟翼头部位置。黑色实线表示巡航时的翼型。圆点是巡航襟翼最前缘点在各档位的位置轨迹。可以看出,在整个变弯过程中,襟翼前缘的运动轨迹大体上平行于机翼下表面。这可以保证在变弯过程中不会引起下表面过大的曲率变化。上表面通过扰流板的偏转保证翼型表面连续无缝。

图5　巡航阶段襟翼运动轨迹

引入典型的简单铰链机构(即定轴转动,波音B787及空客A350XWB均采用类似机构,文中以simplehingedflap表示)的圆弧轨迹进行对比分析TEVC机构起飞着陆阶段运动学特性。根据TEVC襟翼机构输出的襟翼最大偏角时的位置,设计了可得到相同位置时简单铰链机构。并同样进行了运动仿真,输出轨迹。

图6为两机构输出的轨迹及起飞着陆阶段襟翼相同偏角时的位置。以实线表示变弯度机构输出的轨迹,虚线表示简单铰链机构所对应的轨迹。图中标示出了起飞阶段3个襟翼偏角(15°、17°、20°)及着陆阶段3个襟翼偏角(33°、35°、37°)时襟翼位置及前缘点的轨迹。

图6　起飞着陆阶段襟翼运动轨迹

飞机起飞阶段需要合适的Cl及L/D。在起飞阶段,增加襟翼偏角提高Cl的同时,会减小L/D。因此要求起飞阶段襟翼机构在相同襟翼偏角时有尽可能大的富勒运动以增加升力来提高起飞阶段的L/D[12]。起飞阶段相同襟翼偏角时,变弯度机构比简单铰链机构可产生较大的富勒运动。如在襟翼偏角为20°时沿x方向后退量,前者比后者增加25%。

而在着陆阶段,飞机要求有最大的升力系数。变弯度机构襟翼偏角从33°增大到37°沿x方向后退量为简单铰链机构后退量的52%,即襟翼大偏角

时,小的后退量便能产生大的襟翼偏角变化,能保证着陆阶段较快的达到最大升力系数。

3后缘变弯度系统对增升装置效率的影响

民机应具有良好的高升力系统(增升装置)以提供良好的起飞和着陆性能,进而保证飞机的总体性能。对于一架典型的大型双发民航机:着陆时,在固定进场速度条件下,1.0%的最大升力系数增量可以转化为相当于多载22名旅客或1 995kg货物;对于给定的飞机航程,起飞阶段升阻比提高1%可以转化为相当于多载14名乘客或1 270kg货物[12]。以上数据说明了增升装置气动特性相对较小的改变量也会对飞机重量和性能产生大的影响。因此,TEVC系统应具有较高的増升装置效率,保证飞机的起飞着陆性能。

3.1起飞构型气动性能分析

在相同缝翼偏角(20°)的条件下,对TEVC系统及简单铰链机构(simplehinge)不同的襟翼偏角15°和20°进行计算。TEVC构型扰流板下偏3°使两构型缝道宽度相同,如图7a)所示。计算状态为海平面大气状态,Ma=0.2,Re=30×106。

图7　起飞构型及计算结果

图7b)和图7c)为起飞阶段升力系数曲线和升阻比曲线。对于应用同一机构的起飞构型,襟翼偏角越大,增升装置的升力系数越大,失速迎角减小。升阻比随着襟翼偏角的增大而减小。因此,起飞阶段需要确定合适的襟翼偏角以保证满足起飞要求的升力系数及升阻比。

对于应用不同机构的起飞构型,TEVC比简单铰链起飞构型升力线线性段平均增加0.05,最大升力系数提高0.5%。升力线线性段迎角对应的升阻比的增加量从3%减小到0.2%。

一方面TEVC机构使襟翼有较大的后退量,另一方面扰流板下偏增大了主翼的弯度使应用该机构的增升装置有更好的起飞性能。

3.2着陆构型气动性能分析

本节针对应用TEVC机构的偏转扰流板的着陆构型与相同缝道参数的未偏转扰流板的着陆构型(命名为landing)进行了计算及比较。其中缝翼偏转30°,襟翼偏转35°,扰流片下偏3.7°。图8a)为两着陆构型几何外形对比。

图8b)和图8c)分别为两构型的升力及升阻比曲线。TEVC机构的失速迎角比着陆构型小1°,最大升力系数增加1.14%,且线性段上移0.15。

升力的增大主要是由主翼上升力增大引起的,扰流板下偏增加了主翼的弯度,使主翼升力增加明显。同时,TEVC构型在失速迎角前的大部分区域阻力与另一着陆构型相近。因此,失速迎角前的区域下偏扰流板后的TEVC机构升阻比均高于相同缝道参数的扰流板未偏的常规构型。

图8　着陆构型及计算结果

4后缘变弯度对气动性能的影响

4.1二维翼型后缘变弯度对气动性能的影响分析

为了研究利用本文机构实现巡航机翼后缘变弯度在气动上所能产生的收益,本文先在二维巡航翼型基础上进行变弯度的计算及研究,重在研究后缘变弯度对二维翼型气动方面影响变化的趋势。

本文参考波音B787的变弯策略,巡航构型后缘襟翼向上向下最大偏转1.5°,每隔0.5°设一个档位。同时偏转扰流片使翼型上表面连续无缝。在设计升力系数0.6,马赫数为0.729,单位米雷诺数为6.69×106状态下进行计算。

图9a)给出了后缘不同偏角时升力系数曲线,可看出翼型后缘变弯度不改变升力线的斜率,而是改变了翼型的零升迎角。翼型后缘下偏角度越大,相同迎角下的升力系数越大。图9b)所示为1°迎角时后缘偏转不同角度对应的压力分布。

图9　二维翼型后缘变弯计算结果

后缘弯度增大使其环量增大,对前缘上表面产生正的诱导速度,上表面流速加快,压力减小,负压峰值增高。下表面流速变慢,压力增大,因此,升力增大。同时,上表面流速加快使激波强度增强,激波位置后移。

图9c)给出了后缘不同偏角时的升阻比曲线变化。在升力系数较小时,自由来流为负迎角。后缘上偏可增大相同升力系数时的来流迎角,减小压差阻力,增大了升阻比;升力系数较大时,后缘下偏可减小相同升力系数时的来流迎角,进而减弱激波强度及阻力,提高升阻比。值得注意的是,计算所用的翼型为直接截取的三维Wingbody的KINK处翼型,在设计升力系数0.6时升阻比并非最大。后缘下偏1.5°时,升阻比相比于初始翼型提高了6.8%。

图10为定升力系数Cl=0.6时阻力发散特性曲线。阻力发散马赫数(dCd/dMa=0.1)随后缘弯度增大而增大,即后缘偏角增加可提高阻力发散马赫数,改善翼型的阻力发散特性。

图10　Cd随Ma变化曲线

4.2翼身组合体后缘变弯度对气动性能的影响及分析

为了减少网格量,降低计算难度,缩短计算的时间,本文在某远程宽体飞机翼身组合体上对TEVC系统进行计算和评估,旨在研究增升装置机构实现后缘变弯度及在气动上的收益,未考虑副翼、前缘缝翼参与变弯度及其对气动的影响。

CATIA三维模型如图11所示。通过KINK处机构输出的变弯位置,利用刚体运动,可分别确定内外段襟翼的偏转,进而确定后缘襟翼不同偏角时的变弯构型。配合扰流板下偏,使上下翼面连续无缝。

图11　后缘变弯构型

在巡航马赫数为0.85,单位米雷诺数6.69×106状态下进行计算,设计升力系数为0.515,即对应飞机携带50%机内燃油量时的升力系数。在巡航范围内,对应机体内剩余燃油变化为80%～20%,即确定巡航阶段的升力系数变化范围Cl=0.465～0.565。

采用多块结构网格,近壁面处网格加密,计算网格量为810万,物面网格如图12所示。为了给出正确的比较结果,各变弯构型之间网格数量和分布都分别保持不变,这样就将网格差异引起的流场计算结果的差别减到了最小。

图12　计算网格

本文分别针对后缘几种不同的变弯构型进行了计算:沿弦向弯度变化,即内外段襟翼同时偏转相同角度,如±1.5°(下偏为正,上偏为负)、±1°、±0.5°。沿展向弯度变化,如仅内侧襟翼偏转-0.5°、-1°;仅外侧襟翼偏转0.5°、1°;内外翼段偏转不同角度,如内侧上偏0.5°,外侧下偏0.5°。

表1给出了在设计点,Ma=0.85,Cl=0.515时,几种不同变弯构型相比于初始构型在该设计工况时的阻力及升阻比变化。

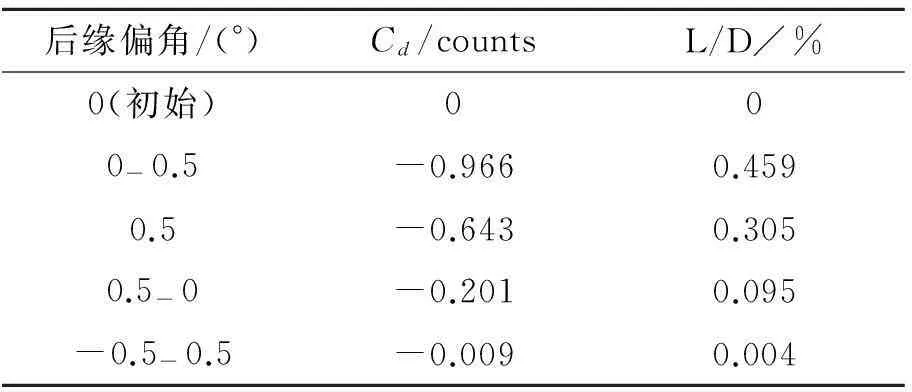
表1　Cl=0.515时阻力系数及升阻比

表1中的几种变弯构型均降低了设计点的阻力系数。仅外翼段下偏0.5°时,阻力降低0.966counts,升阻比提高0.459%。

飞机刚开始进入巡航,即Cl=0.565时,初始构型及不同变弯构型在该工况时的阻力系数及升阻比变化如表2所示。

表2　Cl=0.565时阻力系数及升阻比

表2列出了内外段襟翼同时下偏1°、1.5°、0.5°时的阻力系数。后缘襟翼下偏1°时,阻力降低5.368counts,升阻比提高2.28%。

巡航末端,即Cl=0.465时,初始构型及不同变弯构型在该工况时的阻力系数及升阻比变化如表3所示。

表3　Cl=0.465时阻力系数及升阻比

对比初始构型,仅内翼段襟翼上偏1°时,阻力降低0.665counts,升阻比提高0.345%。

巡航阶段机翼后缘变弯度系统的气动收益可用图13表示。虽然本文变弯度构型存在以下限制条件:计算的构型后缘襟翼弦长较短,沿弦向的弯度变化有限;为了评估本文利用増升装置的变弯效果,后缘未考虑副翼参与变弯,也在一定程度上降低了气动上的收益;襟翼仅分为内外两段,与波音787内襟翼、襟副翼、外襟翼、副翼的四段变弯相比,沿展向的弯度变化有限。但在整个巡航段仍取得了可观的收益,巡航阶段升阻比提高0.345%～2.28%。

后缘变弯度系统通过后缘偏转不同的角度持续优化机翼外形,降低巡航时的阻力。传统的机翼设计局限于仅优化单个设计点(对应50%燃油重量时的升力系数)的翼型或机翼参数,兼顾设计升力系数±0.05变化范围内的阻力特性。而变弯度可为机翼设计提供更多的设计点,在传统机翼设计的基础上,通过优化巡航阶段几个状态时的后缘偏角,可进一步降低巡航阶段的阻力,减少油耗。

后缘弯度变化会改变翼型上表面压力,进而影响激波位置或减弱激波强度来减小阻力。图14至图16分别给出了Cl=0.565时,初始构型与后缘下偏1°时机翼表面的压力云图和19 m站位处的压力分布,可看出襟翼下偏1°后,弯度增加,巡航迎角减小,从而前缘吸力峰值降低,激波位置后移,外翼段激波更弱且位置更向后。

图13　升阻比曲线对比　　　　　　　图14　初始构型表面压力　　图15　后缘下偏1°时表面压云图及极限流线力云图及极限流线

后缘变弯度也会改变机翼展向的环量及升力分布。图17和图18分别给出了Cl=0.465时,最佳椭圆型环量分布与初始构型和仅内翼段襟翼上偏1°构型环量分布对比及对应的升力系数的对比。可看出,变弯后的构型环量更贴近椭圆形分布,有利于减小诱导阻力。

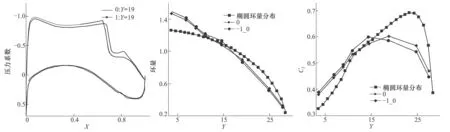
图16　Y=19 m处压力分布对比　　　　　图17　环量分布对比　　　图18　升力系数分布对比

5结论

1) 通过运动仿真对本文研究的増升装置机构进行运动学分析。在巡航阶段变弯度时,襟翼前缘的运动轨迹大体上平行于机翼下表面,这可以保证在变弯过程中不会引起下表面过大的曲率变化。上表面通过扰流板的偏转保证翼型表面连续无缝。与简单铰链机构的圆弧轨迹相比,起飞阶段,即襟翼偏角较小时具有较大的后退量;着陆阶段,即襟翼大偏角时,小的后退量能尽可能大的增加襟翼偏角。该机构良好的运动学特性使其能满足巡航阶段变弯度及起飞着陆的要求。

2) 评估了可用于机翼变弯度的襟翼机构对增升装置效率的影响,与简单铰链机构起飞构型以及传统着陆构型相比,应用该机构的起飞着陆构型,线性段及最大升力系数、升阻比均有增加,即具有更好的起飞着陆性能,满足增升装置的气动设计要求。

3) 研究了机翼后缘变弯度对其气动性能的影响。后缘变弯度不改变二维翼型的升力线斜率。在升力系数较小时,后缘上偏增大了升阻比;升力系数较大时,后缘下偏提高了升阻比。后缘偏角增加可提高阻力发散马赫数,改善翼型的阻力发散特性。在远程宽体客机翼身组合体基础上改变后缘弯度,巡航段升阻比提高0.345～2.28%之间,验证了本文所研究的增升装置机构在气动上取得了较大的收益。

参考文献：

[1]Bolonkin A, Gilyard G B. Estimated Benefits of Variable-Geometry Wing Camber Control for Transport Aircraft[R]. NASA/TM-1999-206586

[2]Aaron A Tucker, Helen L Reed, William S Saric. Laminar Flow Control Flight Experiment Design and Execution[C]∥52nd Aerospace Sciences Meeting, Maryland, 2014

[3]Preliminary Design Department. Assessment of Variable Camber for Application to Transport Aircraft[R]. Seattle: Boeing Commercial Airplane Company, 1980: 1-89

[4]Szodruch J. The Influence of Camber Variation on the Aerodynamics of Civil Transport Aircraft[M]. Messerschmitt-Bölkow-Blohm, Information and Dokumentation, 1985: 1-5

[5]Kota S. Synthesis of Joint Less Compliant Mechanisms for Adaptive Compliant Wing(ACW)[R]. MI-48109-2125, 2000: 1-13

[6]Guy Norris. Boeing Unveils Plans for Trailing Edge Variable Camber on 787 to Reduce Drag, Save Weight[EB/OL]. (2006-6-12). http:∥Tlightglobal.com/news/articles/.

[7]杨智春,解江. 柔性后缘自适应机翼的概念设计[J]. 航空学报, 2009, 30(6): 1028-1034

Yang Zhichun, Xie Jiang. Concept Design of Adaptive Wing with Flexible Trailing Edge[J]. Acta Aeronoutica et Astronautica Sinica, 2009, 30(6): 1028-1034 (in Chinese)

[8]杨文超, 杨剑挺, 王进, 等. 变弯度机翼准定常流动分离特性的实验研究[J]. 中国科学: 物理学力学天文学, 2012, 42: 531-537

Yang Weicao, Yang Jieting, Wang Jin, et al. Experimental Investigation on the Quasi-Steady Flow Separation Behaviors of a Variable Camber Wing[J]. Sci Sin Phys Mech Astron, 2012, 42: 531-537 (in Chinese)

[9]John D Anderson. 计算流体力学基础及其应用[M]. 吴颂平, 刘赵淼, 译. 北京: 机械工业出版社, 2007: 52-59

John D Anderson. Computational Fluid Dynamics[M]. Wu Songping, Liu Zhaomiao, Translator. Beijing, China Machine Press, 2007: 52-59 (in Chinese)

[10] Menter F R. Zonal Two-Equation K-W Turbulence Model for Aerodynamic Flows[R]. AIAA-1933-2906

[11] Sakurai S, Wheaton J M, Fox S J, et al. Aircraft Flap Mechanism Having Compact Large Fowler Motion Providing Multiple Cruise Positions[P]. US:2013/0075537 A1. 3,28, 2013

[12] Smith Amo. High-Lift Aerodynamics[J]. Journal of Aircraft, 1975, 12(6): 501-530

Mechanical Simulation and Aerodynamic Analysis on a New Type of Wing Trailing Edge Variable Camber

Shen Guangchen, Bai Junqiang, Liu Nan, Liu Rui

(School of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:By using computational fluid dynamics and CATIA DMU Kinematics, a high-lift system that could be used on the present and future civil aircraft for varying wing camber during cruise has been studied. It consists of flap mechanism and drooping spoiler. Kinematic analysis of the flap mechanism shows that there won't be any gap on the wing surface during cruise. Besides, the track of flap meets the requirements of takeoff and landing. Compared with the simple hinged flap, the linear range of lift coefficient of takeoff configurations that applied the flap mechanism increases by 0.05, and the corresponding increase of lift to drag ratio is from 3% to 0.2%. The maximum lift coefficient of landing configuration with drooping spoiler increases by 1.14% and the linear range of lift coefficient increases to 0.15 than the configuration without spoiler droop, which demonstrates its high efficiency. The flap mechanism has been used to change trailing edge camber on the basis of 2D cruise foils and the lift to drag ratio has been improved. The drag-divergence Mach number increases with trailing edge deflection angle. The flap mechanism has also been used to change trailing edge camber of a long-range, wide-body transport aircraft. In the entire range of lift coefficient available during cruise, the L/D of initial configuration has increased by 0.345%～2.28%. In conclusion, the high-lift system used for varying camber during cruise shows great benefits on aerodynamics without increasing complexity and weight of mechanism.

Keywords:high-lift system; aerodynamics; mechanisms; trailing edge variable camber; computational fluid dynamics; aerodynamic configurations; lift to drag ratio; Mach number

收稿日期：2016-03-08

作者简介：沈广琛(1991—),西北工业大学硕士研究生,主要从事飞行器气动外形优化设计研究。

中图分类号：V211.3

文献标志码：A

文章编号:1000-2758(2016)04-0578-09