电机转速环节Super-Twisting算法二阶滑模控制律设计与研究

张庆超, 马瑞卿, 皇甫宜耿, 王姣

(1.西北工业大学 自动化学院, 陕西 西安　710129; 2.中国兵器第203研究所, 陕西 西安　710065)



电机转速环节Super-Twisting算法二阶滑模控制律设计与研究

张庆超1, 马瑞卿1, 皇甫宜耿1, 王姣2

(1.西北工业大学 自动化学院, 陕西 西安710129; 2.中国兵器第203研究所, 陕西 西安710065)

摘要：针对电机转速环节，研究了以Super-Twisting算法(STA)为基础的转速闭环二阶滑模控制律设计方法，无需对转速求导或求解转速极值。利用Lyapunov函数证明了系统的稳定性，并分析了系统中比例滑模项对系统收敛的稳定性和快速性的影响，以及不同类型比例滑模项的共同点与区别。仿真结果表明，在STA基础上人为增加比例滑模项可以提高系统的收敛速度，而不受系统工作状态影响，并且不改变系统的STA二阶滑模特性。由于各种电机都具有统一的转子运动方程，因此，研究结果对各种电机的转速环节二阶滑模闭环控制具有通用性。

关键词：电机；转速闭环；二阶滑模；Super-Twisting算法；稳定性；收敛性

滑模控制由于对系统匹配的有界不确定扰动具有强鲁棒性，在各种电机控制系统中得到了广泛关注与研究[1-6]。在高性能转速、电流/转矩双闭环电机调速系统结构，转速外环控制律输出就是内环的给定，要求是连续控制指令。但传统滑模控制是一种非连续控制方法，输出控制信号存在离散化的高频抖振，导致传统滑模不适合用于多环级联系统的外环控制。

针对传统滑模控制中的抖振问题，众多学者提出了多种抖振抑制方法，例如趋近律法、边界层法、高阶滑模等，并将其用于各种电机控制系统中[1-2,5-6]。在这些方法中，高阶滑模控制是一种既能够保留传统滑模强鲁棒性，又能够有效抑制抖振的新型滑模控制方法，而考虑到电机系统阶数以及控制律复杂性，电机调速系统通常采用二阶滑模。

常见的二阶滑模控制算法有Twisting算法、Super-Twisting算法、Sub-Optimal算法、Drift算法和Prescribed Convergence Law算法等[7-9]。其中，Super-Twisting算法(Super-Twisting Algorithm,STA)由于无需求取滑模变量的导数或极值，且输出控制信号连续无抖振，因此，被广泛应用于各种电机调速控制中[3-4,10-12]。

文献[3]将STA用于开关磁阻电机调速控制；文献[4]将STA用于风力发电系统中绕线转子感应发电机的转矩控制；文献[10]将STA用于有刷直流电机调速控制；文献[11]将STA用于BLDCM的高性能转速控制；文献[12]将STA用于永磁同步直线电机的速度控制。但上述方法都属于电机的单转速闭环二阶滑模控制，无法控制电流，并且需要对转速求导，增加了系统引入干扰、噪声等风险。

对于电机的双闭环滑模控制，文献[13]对采用指数趋近律法的BLDCM转速、电流双闭环滑模控制进行了仿真研究；文献[14]提出一种基于高阶非奇异终端滑模的控制方法，用于永磁同步电机的转速、电流双闭环控制；文献[15]将二阶滑模Sub-Optimal算法用于永磁直流电机的转速、电流双闭环控制；文献[16]将二阶积分滑模用于永磁同步电机的转速外环控制。上述双闭环滑模控制方法，也都需要对转速求导或求导数为零处的滑模变量极值。

本文针对电机双闭环系统中转速外环的二阶滑模控制，基于STA设计了二阶滑模控制律，无需对转速求导或求极值；利用Lyapunov 函数证明了系统的稳定性，并分析了比例滑模项对系统收敛的稳定性和快速性的影响，在此基础上，设计了带有比例滑模项的电机转速外环STA 二阶滑模控制律；最后，根据系统特点，结合仿真分析了不同类型的比例滑模项的共同点与区别。

1电机转速环节误差状态方程

对于各种旋转电机，例如无刷直流电机、永磁同步电机、开关磁阻电机、异步电机、直流电机等，其转子运动方程都可以统一表示为

(1)

式中,Te为电磁转矩;Tl为负载转矩;J为电机等效转动惯量;ω为转子角速度;β为黏滞摩擦系数。

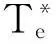
(2)

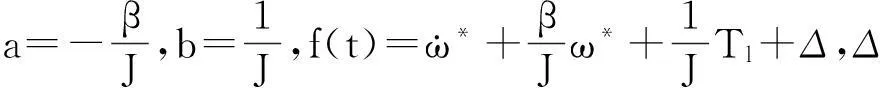
2控制律设计与稳定性分析

2.1控制律设计

二阶滑模STA的具体表达式可写为[7]

(3)

式中,s为滑模变量,而控制参数α>0,λ>0。

STA是一种针对相关度为1的系统提出的二阶滑模控制算法,而显然(2)式所示的电机转速误差状态方程的相关度为1,因此,设计滑模面为

(4)

针对(2)式,可设计基于STA的直接控制律为

(5)

将(5)式带入(2)式,并对(4)式沿(2)式所示系统轨迹求导可得

(6)

在(6)式所示的闭环系统中,λ′=bλ,α′=bα,γ=β/J=-a。显然,γ为电机参数,并且γ>0。在控制律的参数调节过程中,可将系统参数b融入控制参数λ′和α′整体调节,而无需关注b的实际准确值。这样,即使在不知道电机转速环节确切的模型参数的条件下,对于(6)式所示系统,仍然只有2个控制参数需要调节λ和α。

2.2稳定性分析

对于STA的稳定性分析,文献[18-19]提出了一种相对简单的利用类二次型Lyapunov函数的证明方法,并分析了常值扰动与时变扰动2种情况下的STA收敛性;而实际上,常值扰动可以作为时变扰动的一个特例,因此,这里仅从时变扰动角度,借鉴文献[18-19]构造的Lyapunov函数,对(6)式所示系统进行稳定性证明。

令φ=f(t),并采用变量代换

(7)

则,(6)式可以改写为

(8)

至此,(5)式所示控制律设计的稳定性分析问题就转化为(8)式所示系统的平衡点镇定问题。

针对(8)式所示系统,选取Lyapunov函数

(9)

(9)式所示V(z)是连续正定函数,除集合外{z1=s=0},V处处可微,对V沿系统轨迹求导有

(10)

式中

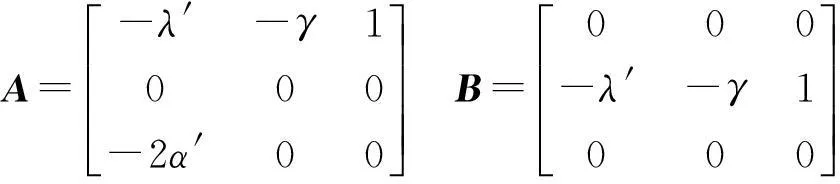
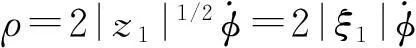
(11)

令m=CTΠξ=ξTΠC,则m2=ξTΠCCTΠξ,根据不等式(m-ρ)2=m2-2mρ+ρ2≥0,∀m,ρ∈R,可以推出

(12)

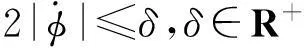
(13)

结合(10)式可得

(14)

式中

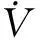
(15)

而根据Schur补定理,可推出Q1为正定矩阵的一个充分条件为

(16)

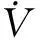
(17)

此时

(18)

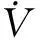
(19)

式中

(20)

从而可知,当参数满足(21)式时

(21)

根据(19)式可推出

(22)

综合(15)式～(22)式可知,系统控制参数应满足(23)式所示条件

(23)

在此条件下,对(9)式所示的连续正定候选Lyapunov函数V=ξTΠξ的沿系统轨迹求导有

(24)

那么,(6)式所示系统满足Lyapunov稳定性条件。

2.3比例滑模项对系统稳定性及收敛速度影响

1) 稳定性影响分析

当对(2)式所示的电机转速误差方程直接采用STA时,如(6)式所示,相比文献[17-20]中分析的纯STA系统多出一个关于滑模面的比例项-γs。而根据(7)式～(24)式的稳定性分析过程可知,只要保证γ>0,-γs就不影响系统的稳定性。而对于γ=β/J,其中β和J都是电机的实际物理参数,并且β>0,J>0,所以γ>0是客观参数条件。

2) 控制律改进与收敛速度影响分析

既然比例滑模项不影响电机转速环节二阶滑模STA闭环控制的稳定性,那么可通过人为地增加比例滑模项ks(k>0)把控制律(5)式改为

(25)

将(25)式带入(2)式,并对(4)式沿(2)式所示系统轨迹求导可得

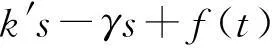
(26)

式中,k′=bk。

对于(26)式所示的系统,当把k′+γ视为一个整体参数时,参照(7)式～(24)式的稳定性分析过程,结合上述分析,可知在原STA控制律中加入比例项ks,亦不影响原系统的稳定性对于控制律(25)式,相比(5)式所示的纯STA控制律中的开方滑模比例项——λ|s|1/2sign(s),只要合理设置k、ks的引入可以增加系统在远离平衡点处的滑模变量增益,增大控制指令输出,保证鲁棒性,并提高收敛速度;在到达平衡点附近时,STA起到主导作用,保证系统在平衡点邻域内的稳定性和鲁棒性。

3仿真与分析

本文以BLDCM双闭环调速系统为例,进行相关仿真与分析,系统原理框图如图1所示,其中直流母线电压Ud=UN=270V。为了快速响应转速外环控制律输出的连续控制指令,转矩内环设置为基于三相六状态换相逻辑的一阶滑模转矩控制[21]。

3.1仿真参数设置

1) 电机参数

系统仿真模型中的BLDCM参数如表1所示。

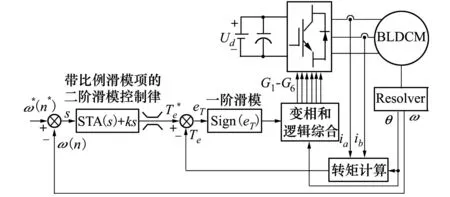
图1　带比例滑模项STA的BLDCM双闭环控制原理框图

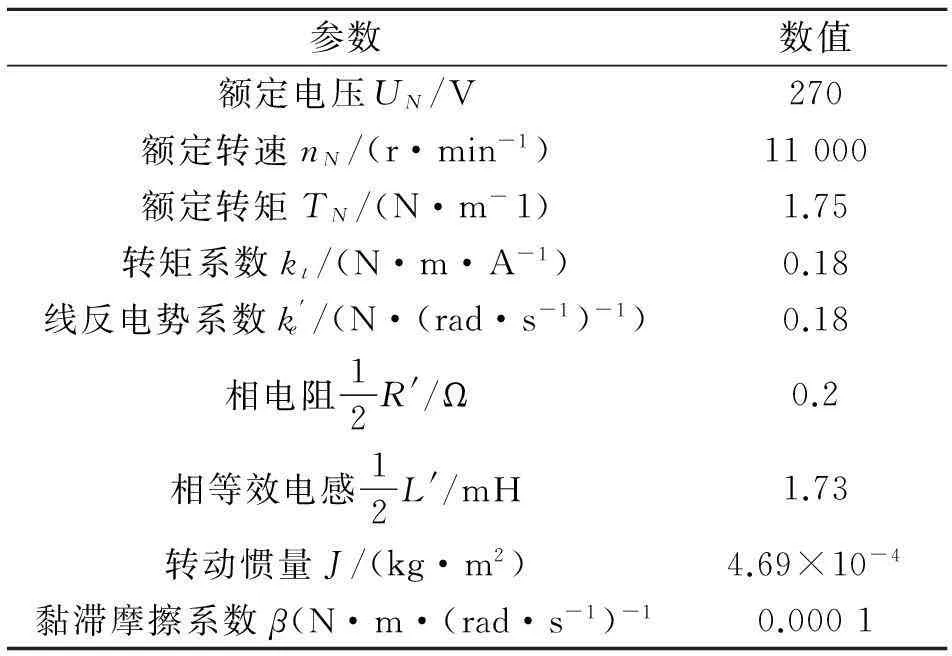
参数数值额定电压UN/V270额定转速nN/(r·min-1)11000额定转矩TN/(N·m-1)1.75转矩系数kt/(N·m·A-1)0.18线反电势系数k'e/(N·(rad·s-1)-1)0.18相电阻12R'/Ω0.2相等效电感12L'/mH1.73转动惯量J/(kg·m2)4.69×10-4黏滞摩擦系数β(N·m·(rad·s-1)-10.0001

2) 控制参数

(23)式所示的控制参数λ′(λ′=bλ)和α′(α′=bα)的取值条件,只是一个能够在理论上保证系统稳定性的充分条件,并非实用条件和最优控制参数,而最终的控制律参数调节应该归结为对λ和α的设置。为了更加合理地进行系统仿真分析,以及分析不同控制参数变化对系统稳定性和收敛速度的影响,在系统仿真模型中,按照(25)式设计带比例滑模项的STA二阶滑模控制律,并设置如表2和表3所示的控制参数。

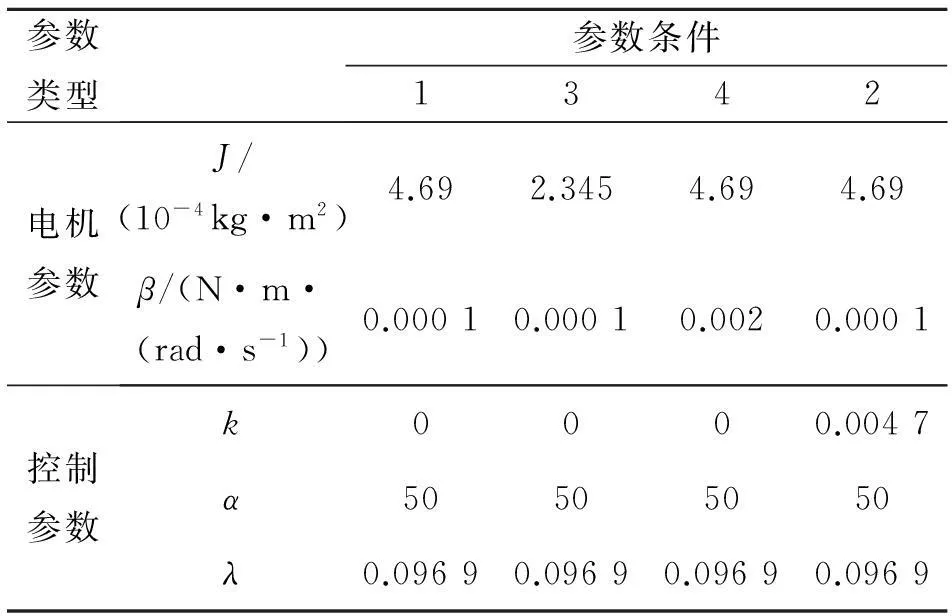
表2　空载运行仿真参数设置

表3　带扰动负载运行仿真参数设置

3.2空载运行分析

令BLDCM在空载条件时(此时,δ=0),设置控制参数如表2所示。在此条件下,系统在给定转速n*=8 000 r/min(对应ω*=837.7 rad/s)时的空载转速、转矩响应波形如图2和图3所示。

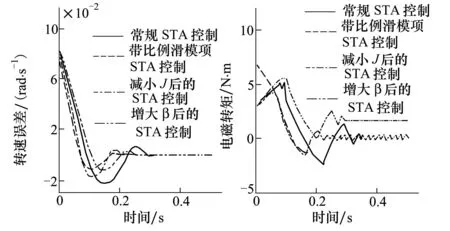
图2　空载时,不同参数条件下的转速误差收敛曲线　图3　空载时,不同参数条件下的电磁转矩曲线

图2和图3中的曲线1～4分别对应于在表2中参数条件1～4所示参数设置下的转速误差和电磁转矩仿真结果,其中,参数条件2为添加比例滑模项后的参数设置,参数条件3为减小J后的参数设置,参数条件4为增大β后的参数设置。

1)k与γ的区别以及对系统收敛性的影响

由(26)式可知,k和γ在电机转速环节二阶滑模控制系统中,同样属于比例滑模项的增益,但不同的是,k是在STA二阶滑模控制律中人为增加的比例滑模项增益,而γ=β/J显然是电机及其传动系统的固有参数。结合表2和图2可知,人为添加比例滑模项ks和增大γ都可以提高滑模比例项增益,从而提高系统的整体收敛速度。

由于γ=β/J,因此,增大β和减小J都可以增大γ。但是,增大β意味着要增加系统的摩擦系数,而为了要达到图2中曲线4所示的响应效果,需要将β放大很多倍(仿真中为20倍),这对于实际系统来说,会急剧增大摩擦系数,影响机械结构寿命;并且,如图3中曲线4所示,增大β会令系统摩擦转矩增大,这样即使在空载条件下也需要很大的电磁转矩,例如,对照表1所示的电机额定参数,在空载条件下在8 000 r/min的转速下,由于β的影响,电机转矩已经为1.7 N·m,接近电机的额定负载,这样的系统在实际中显然无法使用。

另外,结合(1)式分析图2中曲线4可知:在电机增速收敛的过程中,βω项为阻力矩,不但没有加速收敛过程,还明显减慢收敛过程;但是,当电机转速在高速区出现超调时,转速误差为负,根据(26)式,增大β等效于令-γs项加速了退饱和。而在实际的物理系统中,在高速区,由于较大的β产生的阻力矩βω很大,同时由于s减小,并且控制算法开始退饱和,导致在此阶段电机的加速度减小,限制了转速超调,同时,增大β后,在减速过程中βω项提高了减速度,从而起到了加快收敛的作用;由此可以看出,β对系统收敛速度的影响会随电机的工作状态变化而变化。

对于通过减小J(仿真中设置为J/2)来提高收敛速度的方法(图2中曲线3),虽然不会出现增大β带来的问题,但是,由于受到电机外形、体积、材料等限制,减小J在实际中的可操作性有限。而在控制律中人为添加比例滑模项ks的方法(图2中曲线2)既不会出现增大β带来的各种问题,也不会受限于电机优化设计中的各种客观条件限制,能够在不影响系统稳定性的前提下,提高系统收敛速度,并且不影响系统的机械结构,不受电机优化设计局限性限制,相对来说是更简单、有效、可行的方案。

2) 系统收敛轨迹

图4和图5分别为系统相平面收敛轨迹和三维收敛轨迹。图4和图5中的曲线1、曲线2分别为在表2中参数条件1、参数条件2下的仿真结果。

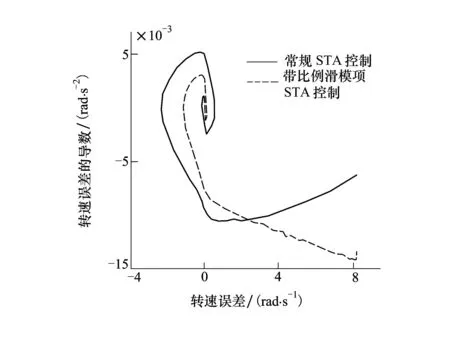
图4　空载下系统相平面轨迹

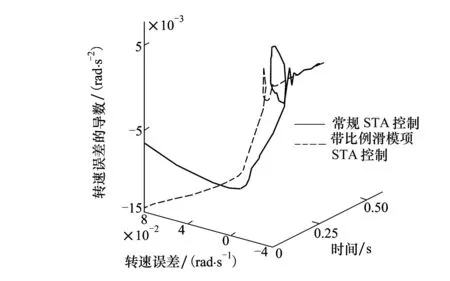
图5　空载下系统三维收敛轨迹

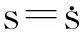
由图5可以看出,设置合适增益系数的比例滑模项,可以提高系统在远离平衡点的收敛速度,并且能在收敛到平衡点的过程中,“收紧”收敛范围,减小系统超调,提高收敛速度。

3.3带扰动负载运行分析

为了发挥系统的最优动、静态性能和鲁棒性,本文通过参数试凑法,在系统仿真模型中确定了一组最优的λ和α取值,列于表3中。图6a)、图7和图8分别为系统在图6b)所示扰动负载条件下转速误差收敛曲线、系统相平面轨迹、系统三维收敛轨迹,图中的曲线1和曲线2分别对应为在表3所示的控制参数条件1和参数条件2下的仿真结果。

由图6a)可以看出,设置合适的控制参数后,系统采用二阶滑模控制时对于可微的有界时变负载扰动的强鲁棒性,而曲线2说明,在控制律的基础上人为加入比例滑模项可以进一步减小系统转速超调,并提高对阶跃突变负载扰动的鲁棒性。

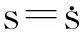
由图8所示的三维收敛轨迹展示了系统在扰动负载条件下的收敛全过程。与空载条件不一样的是,为了满足系统在扰动负载条件下的鲁棒性要求,在(25)式所示的控制律中设置了足够大的参数增益,由于系统中必要的电流限幅,添加比例滑模项后,并没有明显增加系统在远离平衡点的收敛速度。但是,在接近平衡点的收敛过程中,同空载条件一样,比例滑模项的加入能够加速退饱和,“收紧”收敛范围,减小系统超调。

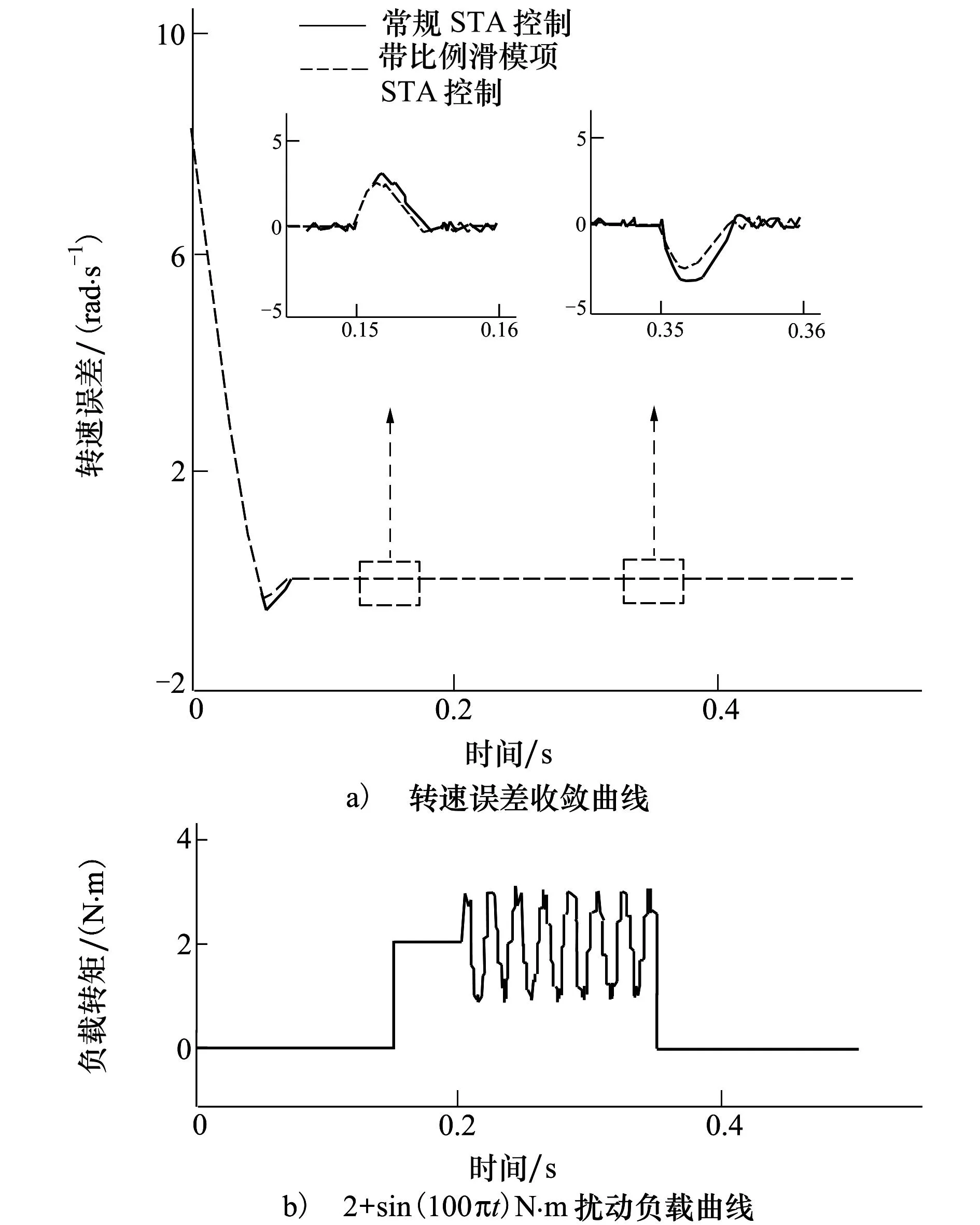
图6　扰动负载条件下,的转速误差收敛曲线

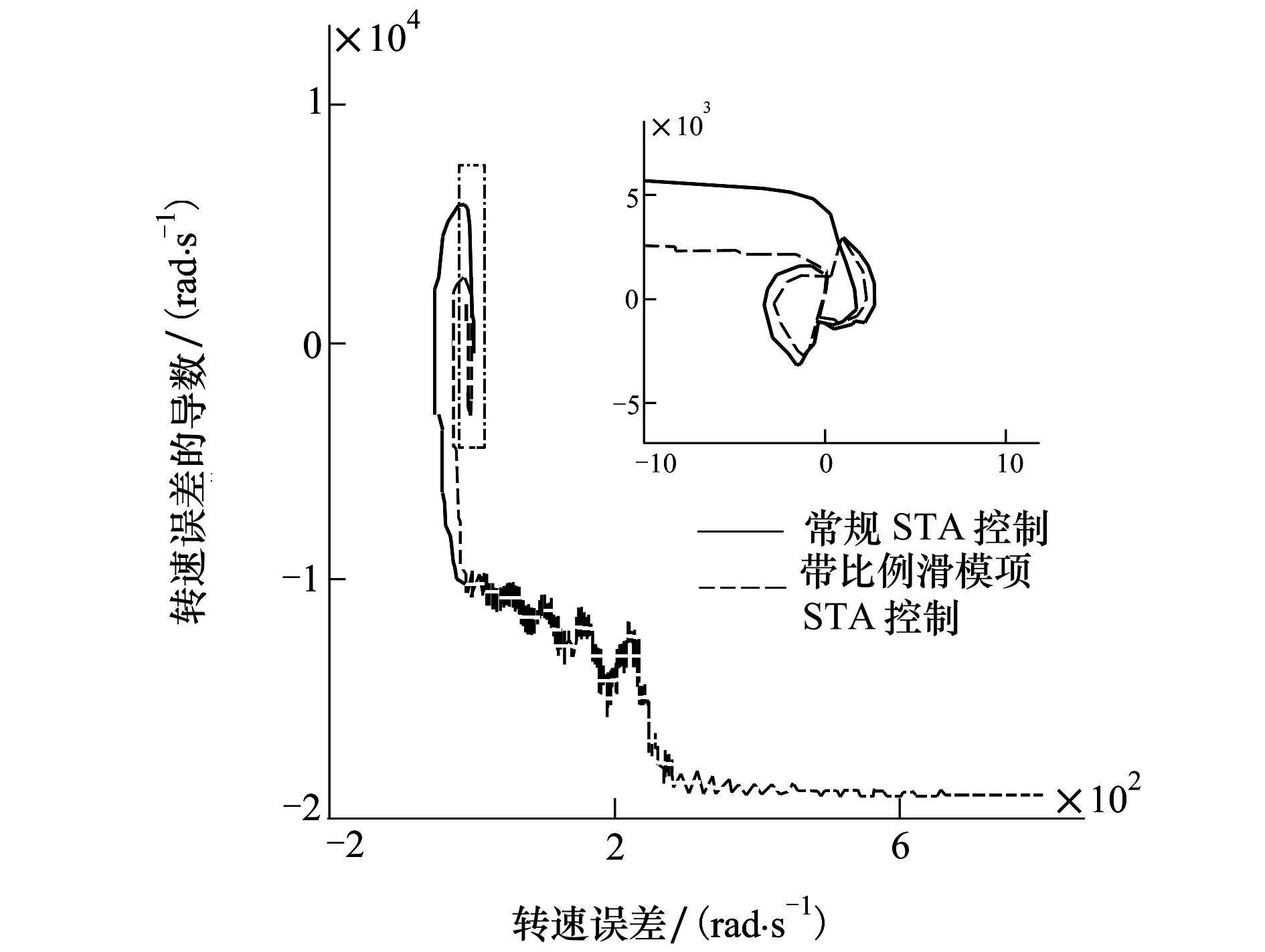
图7　扰动负载条件下的系统相平面轨迹

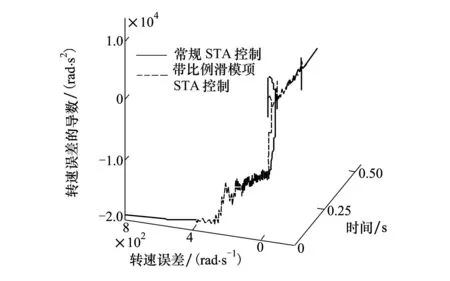
图8　扰动负载条件下的系统三维收敛轨迹

4结论

针对电机转速外环控制,直接采用二阶滑模STA设计闭环控制律时,无需任何变量的导数,可避免求导对系统带来的不利影响,并且控制律能够输出连续控制指令,符合外环控制律设计需求。

采用类二次型Lyapunov函数方法证明了所设计的二阶滑模转速环节闭环控制系统的稳定性,并且证明了比例滑模项不影响系统的稳定性,可以通过人为引入比例滑模项提高系统的收敛速度。

分析了系统中比例滑模项增益系数k与γ的区别:γ体现的是系统的结构参数对于系统收敛性的影响,γ对于系统收敛速度的影响随系统加速或减速的工作状态变化;而k体现的是系统的控制参数对于系统收敛性的影响,k能够提高系统远离平衡点时的收敛速度,并且加速收敛的作用不受系统加速或减速的工作状态变化。

各种电机(包括永磁同步电机、无刷直流电机、永磁直流电机、开关磁阻电机、异步电机等)的转子运动方程都具有统一的形式,因此,本文研究结果在各种电机的应用中均具有通用性。

参考文献：

[1]In-Cheol B, Kyeong-Hwa K, Myung-Joong Y. Robust Nonlinear Speed Control of PM Synchronous Motor Using Boundary Layer Integral Sliding Mode Control Technique[J]. IEEE Trans on Control Systems Technology, 2000,8(1): 47-54

[2]Fu-Juay C, Shih-Hsiung T, Shyang C. Tracking Control of DC Motors Via an Improved Chattering Alleviation Control[J]. IEEE Trans on Industrial Electronics,1992, 39(1): 25-29

[3]Rafiq M, Rehman S U, Rehman F U, et al. A Second Order Sliding Mode Control Design of a Switched Reluctance Motor Using Super Twisting Algorithm[J]. Simulation Modelling Practice & Theory, 2012, 25(6): 106-117

[4]Morfin O A, Loukianov A G, Ruiz R, et al. Torque Controller via Second Order Sliding Modes of WRIG Impelled by DC-Motor for Application in Wind Systems[C]∥Proceedings of the American Control Conference, 2012: 985-990

[5]张晓光, 赵克, 孙力,等. 永磁同步电动机滑模变结构调速系统新型趋近率控制[J]. 中国电机工程学报, 2011, 31(24):77-82

Zhang Xiaoguang, Zhao Ke, Sun Li, et al. A PMSM Sliding Mode Control System Based on A Novel Reaching Law[J]. Proceedings of the CSEE, 2011, 31(24): 77-82 (in Chinese)

[6]Ahmed F S, Laghrouche S, El Bagdouri M. Second-Order Sliding Mode Based Output-Feedback Control of an Engine Air Path Actuator in Presence of Uncertainties[C]∥2010 Conference on Control and Fault-Tolerant Systems, 2010: 50-56

[7]Levant A. Sliding Order and Sliding Accuracy in Sliding Mode Control[J]. International Journal of Control, 1993, 58(6): 1247-1263

[8]Levant A. Principles of 2-Sliding Mode Design[J]. Automatica, 2007,43(4): 576-586

[9]Bartolini G, Ferrara A, Usani E. Chattering Avoidance by Second-Order Sliding Mode Control[J]. IEEE Trans on Automatic Control, 1998, 43(2): 241-246

[10] Damiano A, Gatto G L, Marongiu I, et al. Second-Order Sliding-Mode Control of DC Drives[J]. IEEE Trans on Industrial Electronics, 2004,51(2): 364-373

[11] 黄勤, 周海燕, 凌睿. 二阶滑模控制在直流无刷电机转速调节中的应用[J]. 计算机工程与应用, 2011, 47(6): 243-245

Huang Qin, Zhou Haiyan, Ling Rui. Application of Second Order Sliding Mode to Brushless DC Motor Speed Control[J]. Computer Engineering and Applications, 2011, 47(6): 243-245 (in Chinese)

[12] 孙宜标, 杨雪, 夏加宽. 采用鲁棒微分器的永磁直线同步电机二阶滑模控制[J]. 中国电机工程学报, 2007,33: 6-10

Sun Yibiao, Yang Xue, Xia Jiakuan. Second Order Sliding Mode Control for PMLSM Using Robust Differentiator[J]. Proceedings of the CSEE, 2007, 33: 6-10 (in Chinese)

[13] Rath J J, Saha S, Ikkurti H P. Sliding Mode Scheme for Speed and Current Control of Brushless DC(BLDC) Motor[C]∥IEEE-International Conference on Advances In Engineering, Science And Management, 2012: 450-455

[14] 郑剑飞, 冯勇, 陆启良. 永磁同步电机的高阶终端滑模控制方法[J]. 控制理论与应用, 2009, 26(06):697-700

Zheng Jianfei, Feng Yong, Lu Qiliang. High-Order Terminal Sliding-Mode Control for Permanent Magnet Synchronous Motor[J]. Control Theory & Applications, 2009, 26(06): 697-700 (in Chinese)

[15] Pisano A, Davila A, Fridman L, et al. Cascade Control of PM DC Drives via Second-Order Sliding-Mode Technique[J]. IEEE Trans on Industrial Electronics, 2008,55(11): 3846-3854

[16] 齐亮. 基于滑模变结构方法的永磁同步电机控制问题研究及应用[D]. 上海: 华东理工大学, 2013

Qi Liang. Research and Application of Permanent Magnet Synchronous Motor via Sliding Mode Control Methods[D]. Shanghai: East China University of Science and Technology, 2013(in Chinese)

[17] Moreno J A, Osorio M. Strict Lyapunov Functions for the Super-Twisting Algorithm[J]. IEEE Trans on Automatic Control, 2012, 57(4): 1035-1040

[18] 李鹏, 郑志强. 基于类二次型Lyapunov函数的Super-Twisting算法收敛性分析[J]. 控制与决策, 2011, 26(6):949-952

Li Peng, Zheng Zhiqiang. Convergence of Super-Twisting Algorithm Based on Quadratic-Like Lyapunov Function[J]. Control and Decision, 2011, 26(6): 949-952 (in Chinese)

[19] Moreno J A, Osorio M. A Lyapunov Approach to Second-Order Sliding Mode Controllers and Observers[C]∥47th IEEE Conference on Decision and Control, Cancun, Mexico, 2008: 2856-2861

[20] Zhang Qingchao, Ma Ruiqing, Deng Junjun, et al. A Cascade First and Second Order Sliding Mode Control Approach for Speed Control of Brushless DC Motor[C]∥34th Chinese Control Conference, Hangzhou, China, 2015: 3319-3326

Second-Order Sliding Mode Control Based onSuper-Twisting Algorithm for the Speed Outer Loop of Motors

Zhang Qingchao1, Ma Ruiqing1, Huangfu Yigeng1, Wang Jiao2

1.School of Automation, Northwestern Polytechnical University, Xi′an 710129, China2.No.203 Research Institute of China Ordnance Industries, Xi′an 710065, China

Abstract:Aiming at the speed outer close-loop control for the motors, the design method of the second-order sliding mode control law based on the Super-Twisting algorithm(STA) is researched, which doesn′t need the derivative or the extreme value of the speed. The stability is proved by using Lyapunov function. And the influence for the system stability and the rapidity of convergence by the proportional of the sliding mode variable is analyzed, also the commonality and the differences of the various types proportional of the sliding mode variable. Simulation results show that the introduced proportional of the sliding mode variable in STA can improve the convergence speed of the system regardless of the running state of the motor, and the STA second-order sliding mode features of the motor system is not changed. Due to the unified rotor motion equation, the analyzed result of this paper is general to the speed loop second-order sliding mode control for all kinds of motors

Keywords:close-loop control, motor, speed close-loop, second order sliding mode, Super-Twisting algorithm, stability, convergence, Lyapunov function

收稿日期：2015-10-27

基金项目：航空科学基金(2014ZC53037)资助

作者简介：张庆超(1985—)，西北工业大学博士研究生，主要从事稀土永磁电机驱动与伺服控制及滑模控制的研究。

中图分类号：TM351/TP273

文献标志码：A

文章编号:1000-2758(2016)04-0669-08