∞-余纯投射模
施莉娜,王芳贵,熊 涛
(四川师范大学数学与软件科学学院,四川成都610066)
∞-余纯投射模
施莉娜,王芳贵*,熊 涛
(四川师范大学数学与软件科学学院,四川成都610066)
设R是环,F∞表示平坦维数有限的左R-模类.左R-模M称为∞-余纯投射模,指对任意N∈ F∞都有.证明∞-余纯投射模M是投射模当且仅当M∈F∞,同时证明当l.FFD(R)=0时,余纯投射模是∞-余纯投射模.用∞-余纯投射模刻画QF环和CPH环,证明R是QF环当且仅当每一左R-模是∞-余纯投射模,当且仅当每一N∈F∞是内射模.也证明了R是CPH环当且仅当∞-余纯投射左R-模的子模是∞-余纯投射模,当且仅当每一N∈F∞的内射维数不超过1.
余纯投射模;平坦模;∞-余纯投射模;QF环;CPH环
1 预备知识
E.E.Enochs等[1]引入余纯内射模和强余纯内射模的概念,左R-模M称为余纯内射模是指对任意内射左R-模E,都有.左R-模M称为强余纯内射模是指对任意内射左R-模E,及所有i≥1,都有.E.E.Enochs等[2]又提出余纯平坦模和强余纯平坦模的概念.右R-模N称为余纯平坦模是指对任意内射左R-模E,都有.右R-模N称为强余纯平坦模是指对任意内射左R-模E,及所有i≥1,都有.在文献[2]中,可以看到余纯内射模和余纯平坦模在刻画n-Gorenstein环中发挥重要作用.
J.Z.Xu[3]定义了余挠模,R-模M称为余挠模是指对一切平坦模F,有1.并用余挠模刻画了完全环,给出了平坦盖的相关性质.E. Enochs等[4]引入了-挠模的概念,这与余挠模是对偶的.R-模M称为-挠模,是指对一切平坦模F,有HomR(M,F)=0,且,借助于ø-挠模的讨论,给出了模有的平坦包相关性质刻划,相关研究参见文献[1-7].
X.H.Fu等[8]引入了余纯投射模和强余纯投射模的概念,以及n-余纯投射模的概念.用F表示平坦模类,Fn表示平坦维数不超过n的模类.左R-模M称为n-余纯投射模,是指对任何模N∈ Fn,都有;M称为强余纯投射模,是指对任何模N∈F,以及任何i≥1,都有=0;0-余纯投射模也简称为余纯投射模.显然强余纯投射模是n-余纯投射模,n-余纯投射模是余纯投射模.利用余纯投射模的概念,给出QF环的新刻画,证明了R是QF环当且仅当每一左R-模的是余纯投射模.
熊涛等[9]讨论了余纯投射模的遗传性质,引入了CPH环的概念,并且讨论了CPH环与遗传环的关系.环R称为左CPH环,简称为CPH环,是指每一余纯投射左R-模的子模是余纯投射模.相应地,文献[10]也讨论了n-余纯投射模,并利用n-余纯投射模引入相对遗传环的概念.本文引入和讨论∞-余纯投射模的概念,指出投射模、强余纯投射模、∞-余纯投射模、n-余纯投射模和余纯投射模的一些关系,并以此给出QF环和CPH环的一个新刻画,即证明了R是QF环当且仅当每一左R-模是∞-余纯投射模;R是CPH环当且仅当∞-余纯投射左R-模的子模还是∞-余纯投射模,当且仅当左R-模每个平坦维数有限的模N的内射维数不超过1(定理2.10).
在下面正文中所有的模都指左模,并用F∞表示平坦维数有限的模类.
2 ∞-余纯投射模
设R是环,R-模M称为∞-余纯投射模,是指对任何模N∈F∞,都有
1)投射模自然是∞-余纯投射模;
2)对任何n≥0,∞-余纯投射模是n-余纯投射模.
命题2.1 设R是环.如果M是强余纯投射模,则M是∞-余纯投射模.
证明 设M是强余纯投射模,由文献[8],对任意N∈F∞,有,所以M是∞-余纯投射模.
定理2.2 对R-模M,以下各条等价:
1)M是∞-余纯投射模;
2)任何正合列0→N→B→M→0是分裂的正合列,其中N∈F∞;
3)设0→A→B→C→0是正合列,其中A∈F∞,则

也是正合列;
4) 设0→A→B→M→0是正合列,则对任何N∈F∞有

也是正合列.
证明 1)⇔4)因为M是∞-余纯投射模,对任意N∈F∞有正合列


是正合列,于是α*是满射,所以存在h:B→N,使得α*(h)=hα=1N,从而该正合列是分裂的.

是正合列.

由条件HomR(M,E)→HomR(M,E/N)→0是正合列,于是得到正合列,因此有,即M是∞-余纯投射模.
命题2.3 1)设0→A→B→C→0是正合列.若A、C是∞-余纯投射模,则B是∞-余纯投射模.
2)设{Mi}是一簇R-模,则是∞-余纯投射模当且仅当每一Mi是∞-余纯投射模.
证明 1)对任意N∈F∞,由于A、C是∞-余纯投射左R-模,有由正合列

2)对任意N∈F∞,有自然同构1,所以当且仅当右边每一项
命题2.4 设R是交换环,P是投射R-模.如果M是∞-余纯投射R-模,则是∞-余纯投射模.
证明 对任意T-模N,且fdTN<∞.由平坦维数的换环定理,有fdRN≤fdTN+fdRT<∞.设0→N→E→C→0是正合列,其中E是内射T-模,则有下面的2行是正合列的交换图(图1).
推论2.6 设ø:R→T是环同态,且T是平坦右R-模.设M是∞-余纯投射R-模,则是∞-余纯投射T-模.
推论2.7 设R是交换环,S是R-的乘法封闭集.设M是∞-余纯投射R-模,则MS是∞-余纯投射RS-模.
推论2.8 设M是∞-余纯投射R-模,则M[x]是∞-余纯投射R[x]-模.
命题2.9 设R是交换环,P是有限生成投射R-模.如果 M 是∞-余纯投射 R-模,则HomR(P,M)是∞-余纯投射模.

证明 对任意N∈F∞,由文献[12]有自然同构因为M是∞-余纯投射模,则,从而,故HomR(P,M)是∞-余纯投射模.
下面来看什么情况下∞-余纯投射模是投射模.
定理2.10 设M是∞-余纯投射R-模,则M是投射模当且仅当fdRM<∞,于是∞-余纯投射模不是投射模时,一定有平坦维数是无穷大.
证明 设fdRM<∞,0→K→P→M→0是正合列,其中P是投射模,于是K∈F∞.由定理2.4知此正合列分裂,故M是投射模.反之是显然的.
由定理2.12可以得出如下推论:
推论2.11 设w.gl.dim(R)<∞,则每一∞-余纯投射模是投射模.
3 环的刻画
QF环是一个经典的环类.有一些经典的刻画,例如,它等价于说投射模是内射模,或等价于说平坦模是内射模,也等价于内射模是投射模[3].文献[8]证明了R是QF环当且仅当每一R-模是余纯投射模.现在也可以用前面定义的∞-余纯投射模来刻画QF环.
定理3.1 对环R,以下各条等价:
1)R是QF环;
2)每一平坦模是内射模;
3)每一R-模是强余纯投射模;
4)每一R-模是∞-余纯投射模;
5)每一有限生成R-模是∞-余纯投射模;
6)每一循环R-模是∞-余纯投射模;
7)每一N∈F∞是内射模;
8)每一内射R-模的商模是∞-余纯投射模.
2)⇔1)显然.
2)⇔3)设M是R-模.对任何平坦模F,则F是内射模,故对任何k>0,有,因此M是强余纯投射模.
对R的任何左理想I,由假设有R/I是∞-余纯投射模,于是有.因此,N是内射模.
7)⇔2)平凡的.
4)⇔8)这也是平凡的.
8)⇔3)对任意N∈F∞,取正合列0→N→E→M→0,其中E是内射模,M=E/N.由假设M是∞-余纯投射模,因此,从而任何正合列0→N→E→M→0是分裂的,故是N内射模.
在文献[9]中给出了余纯投射遗传环(CPH)的定义.环R称为左CPH环,简称为CPH环,是指余纯投射R-模的子模是余纯投射模,并在文献[9]中指出环R为CPH环当且仅当每个平坦模的内射维数不超过1.下面用∞-余纯投射模给出CPH环的新刻画.
定理3.2 对环R,以下各条等价:
1)R是CPH环;
2)若N是平坦模,则idRN≤1;
3)若N∈F∞,则idRN≤1;
4)∞-余纯投射R-模的子模是∞-余纯投射模;
5)投射R-模的子模是∞-余纯投射模;
6)自由R-模的子模是∞-余纯投射模;
7)R的每个左理想是∞-余纯投射模.

3)⇔5)设0→A→P→X→0是正合列,其中P是投射模,则对任何N∈F∞,由正合列

注意左边方图是推出图,从而有0→K→P→A→B→0是正合列.由假设,K是∞-余纯投射模.由命题2.5的1)有P→A是余纯投射模.由命题2.5的2)有A是∞-余纯投射模.
推论3.3 设R是CPH环,M是R-模,则M是∞-余纯投射模当且仅当对任何N∈F∞,及任何n≥1,有
命题3.4 设R是CPH环,0→A→B→C→0是正合列,如果C是∞-余纯投射模,则A是∞-余纯投射模当且仅当B是∞-余纯投射模.
证明 对任意N∈F∞有正合列
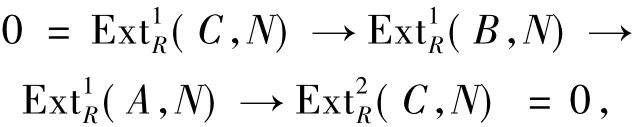
环的左弱finitistic维数为

下面给出余纯投射模是∞-余纯投射模的一个充分条件.
定理3.5 若l.FFD(R)=0,则余纯投射模是∞-余纯投射模.
证明 设 M是余纯投射 R-模.对任何N∈RM,若fdRN<∞,由假设fdRN=0,故N)=0,于是得到M是∞-余纯投射模.
在文献[14]中称环R为右IF环,当且仅当每一内射右R-模是平坦模.当R是左凝聚环时,证明R是右IF环当且仅当R是左FP-内射模.
推论3.6 设R是右IF环,则余纯投射模是∞-余纯投射模.
证明 由 于 R 是 右 IF环,容 易 看 到l.FFD(R)=0.应用定理3.5即得.
推论3.7 环R是右IF环当且仅当R是左凝聚环且每一有限表现R-模是∞-余纯投射模.
证明 设R是右IF环.由文献[15]知R是左凝聚环.由文献[14]得R是FP-内射模,所以每个有限生成自由模是FP-内射模.对任意平坦模N,由文献[11]有N=lim→Fi,其中Fi是有限生成自由模.又因为M是有限表现模,根据文献[16]有

从而M是余纯投射模,由推论3.6得M是∞-余纯投射模.
反之,设M是有限表现R-模,由条件M是∞-余纯投射模,而 R作为 R-模是平坦模,故是FP-内射模.由于R是左凝聚环,引用文献[14]知R是右IF环.
文献[8]定义了模M的余纯投射维数m=cpd(M)为使得对所有i>0,及所有平坦模R-模成立的最小非负整数,也等价
于M的余纯投射分解的最短长度.他们还定义了环的余纯投射维数为

命题3.8 设M是余纯投射模.若cpd(M)≤1,则M是强余纯投射模.
证明 由文献[8]即得.
在文献[17]中定义了环的(左)内射-平坦维数为
l.IFD(R)=sup{fdRE|E是内射模}.文献[17]也证明了若 R是右凝聚环,则 FP-id(RR)=l.IFD(R).
命题3.9 设R是右凝聚环,且FP-id(RR)<∞,则模M是∞-余纯投射模当且仅当M是强余纯投射模.
证明 由文献[8]即得.
例3.10 在文献[10]中已经给出了一个环R,使得对任何n≥2,存在一个(n-2)-余纯投射模不是n-余纯投射模.由此自然得到,对这个环R,以及任何n≥0,存在一个n-余纯投射模不是∞-余纯投射模.
[1]ENOCHS E E,JENDA O M.G.Copure injective modules[J].Quaestiones Math,1991,14(4):401-409.
[2]ENOCHS E E,JENDA O M G.Copure injective resolutions,flat resolutions and dimensions[J].Comment Math Univ Carolin,1993,34(2):203-211.
[3]XU J Z.Flat Covers of Modules[M].Berlin:Springer-Verlag,1996.
[4]ENOCHS E,HEMANDEZ J M,VALLE A D.Coherent rings of finite weak global dimension[J].Proc AMS,1998,126:1611-1620.
[5]DING N Q,CHEN J L.On copure flat modules and flat resolvents[J].Commun Algebra,1996,24(3):1071-1081.
[6]MAO L X,DING L Q.Relative copure injective and copure flat modules[J].J Pure Appl Algebra,2007,208(2):635-646.
[7]SAZEEDEH R.Strongly torsion free,copure flat and Matlis reflexive modules[J].J Pure Appl Algebra,2004,192(1/3):265-274.
[8]FU X H,ZHU H Y,DING L Q.On copure projective modules and copure projective dimensions[J].Commun Algebra,2012,40(1):343-359.
[9]熊涛,王芳贵,胡葵.余纯投射模与CPH环[J].四川师范大学学报(自然科学版),2013,36(2):198-200.
[10]GAO Z H.n-copure projective modules[J].Math Notes,2015,97(1):58-66.
[11]ROTMAN J J.An Introduction to Homological Algebra[M].New York:Springer-Verlag,2010.
[12]王芳贵.交换环与星型算子理论[M].北京:科学出版社,2006.
[13]NICHOLSON W K,YOUSIF M F.Quasi-Frobenius Rings[M].United Kingdom:Cambridge University Press,2003.
[14]JAIN S.Flat and FP-injective[J].Proc AMS,1973,41:437-442.
[15]张力宏.右IF-环及凝聚环的挠理论[J].数学学报,1995,38(1):117-126.
[16]STENSTR M B.Coherent rings and FP-injective modules[J].J London Math Soc,1970,2(2):323-329.
[17]DING N Q,CHEN J L.The flat dimensions of injective modules[J].Manuscripta Math,1993,78(2):165-177.
∞-copure Projective Modules
SHI Lina,WANG Fanggui,XIONG Tao
(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
Let R be a ring and denote by F∞the class of left R-modules with finite flat dimension.A left R-module M is called∞-copure projective iffor all N∈F∞.In this paper we prove that an∞-copure projective module M is projective if and only if M∈F∞,and that if l.FFD(R)=0 then every copure projective left R-module is∞-copure projective.Then we characterize QF and CPH rings in terms of∞-copure projective modules,and prove that R is QF ring if and only if every left R-module is∞-copure projective if and only if every N∈F∞is injective.We also prove that R is CPH ring if and only if every submodule of an∞-copure projective left R-module is∞-copure projective if and only if idRN≤1 for all N∈ F∞.
copure projective module;flat module;∞-copure projective module;QF ring;CPH ring
O154
A
1001-8395(2016)04-0479-05
10.3969/j.issn.1001-8395.2016.04.003
(编辑 郑月蓉)
2015-04-29
国家自然科学基金(11171240)
*通信作者简介:王芳贵(1955—),男,教授,主要从事交换代数、同调代数与代数K-理论的研究,E-mail:wangfg2004@163.com
2010 MSC:16D40;16E30

