垂直指数延伸板驻点混合对流与传热研究

许晓勤，陈淑梅

(1.福建船政交通职业学院汽车运用工程系，福建福州350007; 2.福州大学机械工程及自动化学院，福建福州350116)

垂直指数延伸板驻点混合对流与传热研究

许晓勤1，2，陈淑梅2

(1.福建船政交通职业学院汽车运用工程系，福建福州350007; 2.福州大学机械工程及自动化学院，福建福州350116)

研究不可压缩粘性流体在垂直指数延伸壁面上的二维驻点混合对流与传热问题，借助相似变换将边界层控制方程转换为非线性常微分方程，通过打靶法对其进行数值计算，用图表详细分析顺流和逆流时浮力参数λ和Prandtl数Pr对流体流动和传热特性的影响.结果显示:顺流时，表面摩擦系数和Nusselt数均随浮力参数λ的增大而增大;随着Pr数增大，Nusselt数增大而表面摩擦系数减小.逆流时，表面摩擦系数和Nusselt数均随浮力参数λ的增大而减小，随Pr增大而增大.

垂直指数延伸板;驻点流;混合对流;传热;边界层

0 引言

具有延伸表面边界层流动问题和传热问题显见于科学研究的诸多领域，且具有广阔的应用前景，比如冶金、化工，工业制造工艺中热轧、拔丝、玻璃纤维和造纸、塑料薄膜拉伸、金属聚合物的挤出等领域［1］.HIEMENZ［2］首次介绍了二维驻点流，随后HOMANN［3］又把它扩展成轴对称流动并由HOWARTH［4］加以完善.LAYEK等［5］研究带有热源的多孔延伸板驻点流传热与传质问题，BHATTACHARYYA等做了很多工作，主要研究带抽吸延伸板上驻点流磁流体边界层［6］，过可渗透收缩板的MHD驻点流与传质问题［7］，非均匀热流边界层驻点流传热问题［8］等.国内对这方面的研究比较少，但研究队伍也在不断壮大，如FAN等［9］研究收缩板上非定常驻点流与热传递，XU等［10］研究非定常延伸板上纳米液膜的流动与传热问题，SI等［11］研究多孔膨胀缸的非定常流动与传热问题.值得一提的是，上述文献所提的延伸板大多是线性延伸板，而板的延伸速度不一定呈线性规律，如加速器、发电机等系统的冷却过程，薄膜拉伸、金属聚合物的挤出等都存在非线性现象.非线性拉伸规律有分段函数、二次函数、指数函数等，不同场合有不同的应用.

本文主要研究垂直指数延伸板驻点附近混合对流与传热问题，借助相似变换将边界层控制方程转换为非线性常微分方程，通过打靶法对其进行数值计算，用图表详细分析顺流和逆流时浮力参数λ和Prandtl数Pr对流体流动和传热特性的影响.研究结果对于工程中探讨垂直板上浮力参数及Prandtl数对表面摩擦力和传热特性的特殊影响具有重要意义.

1 控制方程

考虑在二维不可压缩粘性流体在垂直指数延伸壁面上稳态的边界层流动与传热问题.模型示意如图1所示，x轴方向平行于壁面，y轴方向为垂直壁面.壁面沿x方向延伸，延伸速度uw=bex/L，u和v分别为沿着x和y方向的速度分量，υ为流体的运动粘度，L为参考长度.

控制方程:

式中:g为重力加速度;β为热膨胀系数;T为流体温度;α为热扩散系数;ue=aex/L为自由流速度;T∞为外界温度.

边界条件:

引入下列相似变量:

其中:ψ是流函数.根据定义，可知速度分量为:

将速度分量代入式(1)～(3)，可知式(1)自动满足，式(2)和式(3)分别简化为:

式中:λ为浮力参数或混合对流参数，λ=GrL/(ReL)2，其中GrL=gβ(Tw－T∞)L3/υ2是格拉晓夫数［12－13］，ReL=ueL/υ是雷诺数;Pr=υ/α是Prandtl数.注意λ=gβcL/a2是常数，顺流时λ＞0，逆流时λ＜0.

相应边界条件转化为:

其中:ε=b/a为速度比参数.

假定压缩功和摩擦热忽略不计，流体表面摩擦力系数和Nusselt数(表示对流换热强烈程度的一个准数)分别定义为:

此处表面摩擦力τw与热通量qw可以分别写成:

这里μ和κ分别表示动力粘度和导热系数.利用相似变换式(5)可得:

2 数值方法

常微分方程(7)和(8)及边界条件(9)构成两点边值问题，解决此问题的数值方法有同伦分析法(HAM)、Keller－box、Crand－Nicolson法(CNM)、打靶法等.本文采用打靶法进行数值求解，为验证方法的有效性，将方程(7)修改成f－f'2+ff″+ε2=0，边界条件改成f(0)=0，f'(0)=1，f'(∞)=ε，当ε取不同值时，用本方法求得的f″(0)与现有文献结果进行比较，结果很吻合，如表1所示.

表1 ε取不同值时f″(0)值与现有文献比较(λ=0)Tab.1Comparison of f″(0)for different values of ε when λ=0

3 结果与讨论

采用打靶法求解非线性常微分方程(7)和(8)，用图表详细分析顺流和逆流时浮力参数λ和Prandtl数Pr对流体流动和传热特性的影响.表2和表3分别给出当ε=1，λ=±1时不同的Pr对应的f″(0)和－θ'(0)值.图2～11给出表面摩擦系数、Nusselt数、速度和温度分布曲线.

从表2可看出，对于顺流(以λ=1为例)和逆流(以λ=－1为例)，f″(0)几乎大小相等、方向相反，f″(0)都随Pr增大而减小.从表3可得出，对于顺流和逆流，－θ'(0)都是正数，且值均随Pr增大而增大.

表2f″(0)与Pr的关系(ε=1，λ=±1)Tab.2Values of f″(0)for various Prwhen ε=1，λ=±1

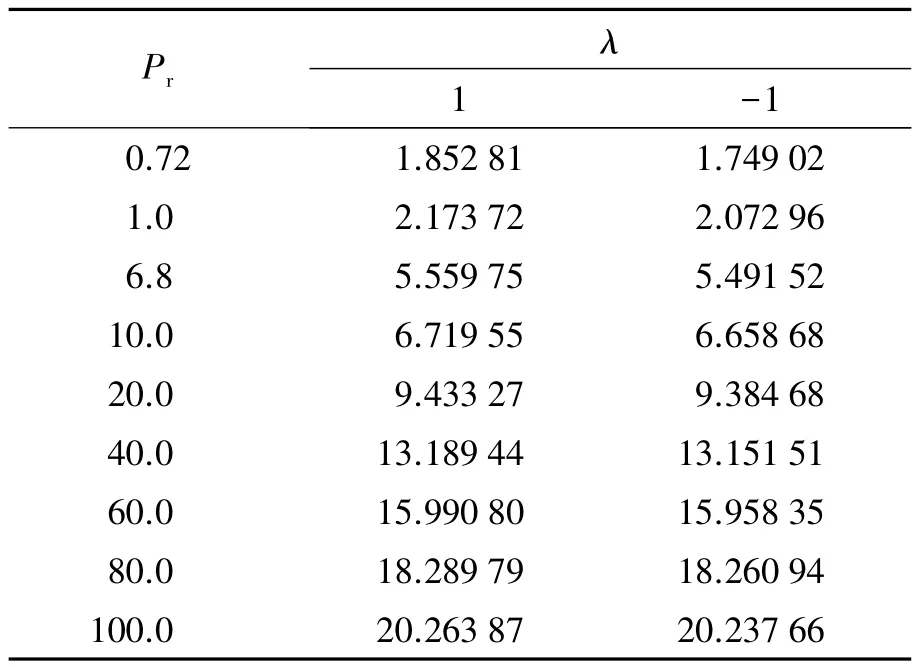
表3 －θ'(0)与Pr的关系(ε=1，λ=±1)Tab.3Values of－θ'(0)for various Prwhen ε=1，λ=±1

从图2和图4可得出，顺流时浮力参数越大，表面摩擦系数越大，而逆流时浮力参数越大，表面摩擦系数越小.这是因为顺流时浮力参数越大，速度越大，壁面剪切应力相应增大，从而使表面摩擦系数增大，而逆流正好相反.从图4还可以看出，所有的曲线都在λ=0处相交，且f″(0)=0，这是因为此时方程(7)与温度无关，流场不受温度场影响;顺流时f″(0)随Pr数增大而减小(这与表1的数据相符合)，这是因为Pr数越大，粘度越大，流动速度越慢，表面剪切应力越小，从而使表面摩擦系数减小，逆流时正好相反.图3显示－θ'(0)与浮力参数λ的关系与f″(0)类似，但对于给定的浮力参数，f″(0)与－θ'(0)随ε的变化方向相反.

图5显示顺流时当Pr不变时，Nusselt数随λ缓慢增加，逆流时情况相反，因为顺流时浮力产生的压力梯度会使流动变快，从而加快表面热传递，而逆流会产生相反的压力梯度，使流动变慢，Nusselt数减小.从图5还可以看出Nusselt数随Pr的增大而增大，因为Pr越大，粘度越大，导热系数越小，从而使－θ'(0)增大.

图6 ～11给出ε，λ和Pr取不同值时的速度与温度分布图.从图6可以看出，流体速度随ε的增大而增大，且ε越大，在壁面处速度梯度越小，与图2相吻合;ε＜1与ε＞1边界层方向相反;对于同样的ε，当ε＜1时顺流的边界层较薄，当ε＞1时逆流的边界层较薄.

从图8和图10可以看出，对于顺流，速度先增加，达到一定值后开始减小，最后达到稳定值，即跟外界速度趋于一致;浮力参数λ值越大，速度变化越明显.这是因为λ值越大，浮力越大，动能越大;流体流动时要克服阻力，因此速度降低，在无穷远处达到一个稳定值.逆流时速度变化趋势正好相反.

从图7、图9和图11可以看出，不管是顺流还是逆流，对所有的ε、λ和Pr值，离壁面越远，温度越小，最后达到稳定值0.这是因为流体从壁面吸热，热能转化为其他形式的能，包括动能.从图11可以看出，Pr越大，热边界层越薄，同时壁面温度梯度值越大(这与表2数据一致)，这是因为Pr大表示热扩散速率会比速度(动量)扩散速率要慢，热边界层厚度就会减小;Pr较小时，浮力对速度和温度分布的影响较明显.

4 结语

垂直延伸板驻点混合对流与传热问题是一基本的物理现象，随着技术进步及科技发展这一问题越来越受到科技及工程人员的重视.本文从理论上研究不可压缩粘性流体在垂直指数延伸壁面上的二维驻点混合对流与传热问题.借助于相似变换将偏微分方程组转换成非线性的常微分方程，通过打靶法对数值计算结果的分析，更加深刻地理解了这一基本物理现象，得到如下结论.

1)对于顺流和逆流，f″(0)几乎大小相等、方向相反，f″(0)都随Pr增大而减小;顺流时浮力参数越大，表面摩擦系数越大，而逆流时浮力参数越大，表面摩擦系数越小;顺流时f″(0)随Pr数增大而减小，逆流时正好相反.在实际应用中应考虑板的延伸方向对壁面摩擦力的影响.

2)对于顺流和逆流，－θ'(0)都是正数，且值均随Pr增大而增大;－θ'(0)与浮力参数λ的关系与f″(0)类似，但对于给定的浮力参数，f″(0)与－θ'(0)随ε的变化方向相反;顺流时当Pr不变时，Nusselt数随λ缓慢增加，逆流时情况相反.

3)流体速度随ε的增大而增大，且ε越大，在壁面处速度梯度越小.速度比ε＜1与ε＞1边界层方向相反;对于同样的ε，当ε＜1时顺流的边界层较薄，当ε＞1时逆流的边界层较薄;对于顺流，速度先是增加，达到一定值后开始减小，最后达到稳定值，即跟外界速度趋于一致;浮力参数λ值越大，速度变化越明显;逆流时速度变化趋势正好相反.流体的流动规律与速度比有关，在实际应用中可通过设计合适的速度比来提高产品质量.

4)不管是顺流还是逆流，对所有的ε、λ和Pr值，离壁面越远，温度越小，最后达到稳定值0;Pr越大，热边界层越薄，同时壁面温度梯度值越大;Pr较小时，浮力对速度和温度分布的影响较明显.

［1］朱婧，郑连存，张欣欣.具有延伸表面的驻点流动和传热问题的级数解［J］.应用数学和力学，2009，30(4):432－442.

［2］HIEMENZ K.Die grenzschicht in einem in dem gleichformingen flussigkeitsstrom eingetauchten gerade kreiszlinder［J］.Dingler’s Polytechnic Journal，1911，326:321－410.

［3］HOMANN F.Die einfluss grosse zhigkeit bei der strmung um der zylinder und um die kugel［J］.Zeitschrift für Angewandte Mathematik und Mechanik，1936，16(3):153－164.

［4］HOWARTH L.On the solution of the laminar boundary layer equations［J］.Proceedings of the Royal Society of London，1938，164(919):547－579.

［5］LAYEK G C，MUKHOPADHYAY S，SAMAD S A.Heat and mass transfer analysis for boundary layer stagnation－point flow towards a heated porous stretching sheet with heat absorption/generation and suction/blowing［J］.International Communications in Heat and Mass Transfer，2007，34(3):347－356.

［6］BHATTACHARYYA K，MUKHOPADHYAY S，LAYEK G C.Reactive solute transfer in magnetohydrodynamic boundary layer stagnation－point flow over a stretching sheet with suction/blowing［J］.Chemical Engineering Communications，2012，199(3): 368－383.

［7］BHATTACHARYYA K，ARIF M G，PRAMANIK W A.MHD boundary layer stagnation－point flow and mass transfer over a permeable shrinking sheet with suction/blowing and chemical reaction［J］.Acta Technica，2012，57(1):1－15.

［8］BHATTACHARYYA K.Heat transfer in unsteady boundary layer stagnation－point flow towards a shrinking sheet［J］.Ain Shams Engineering Journal，2013，44(2):259－264.

［9］FAN T，XU H，POP I.Unsteady stagnation flow and heat transfer towards a shrinking sheet［J］.International Communications in Heat and Mass Transfer，2010，37(10):1 440－1 446.

［10］XU H，POP I，YOU X C.Flow and heat transfer in a nano－liquid film over an unsteady stretching surface［J］.International Journal of Heat Transfer，2013，60:646－652.

［11］SI X H，LI L，ZHENG L C，et al.The exterior unsteady viscous flow and heat transfer due to a porous expanding stretching cylinder［J］.Computers＆Fluids，2014，105:280－284.

［12］ISHAK A，NAZAR R，POP I.Mixed convection boundary layers in the stagnation－point flow toward a stretching vertical sheet［J］.Meccanica，2006，41(5):509－518.

［13］CHEN H.Mixed convection unsteady stagnation－point flow towards a stretching sheet with slip effects［J］.Mathematical Problems in Engineering，2014，2014(1):1－7.

［14］MAHAPATRA T R，GUPTA A S.Heat transfer in stagnation－point flow towards a stretching sheet［J］.Heat＆Mass Transfer，2002，38(6):517－521.

［15］NAZAR R，AMIN N，FILIP D，et al.Unsteady boundary layer flow in the region of the stagnation point on a stretching sheet［J］.International Journal of Engineering Science，2004，15(supp 11/12):1 241－1 253.

(责任编辑:蒋培玉)

Mixed convection and heat transfer of stagnation－point flow towards an exponentially stretching vertical sheet

XU Xiaoqin1，2，CHEN Shumei2
(1.Automobile Application Engineering Dep，Fujian Chuanzheng Communications College，Fuzhou，Fujian 350007，China; 2.School of Mechanical Engineering and Automation，Fuzhou University，Fuzhou，Fujian 350116，China)

The paper studies the mixed convection flow and heat transfer of an incompressible viscous fluid about a stagnation point on an exponentially stretching vertical sheet.The governing equations describing the stagnation point flow are reduced to differential equations by using the similarity transformations and numerically solved through the shooting method.Finally，the effects of the buoyancy parameter and the Prandtl number on the features of the flow and heat transfer characteristics are analyzed and discussed in detail.The results show that for assisting flow，both the skin friction coefficient and the Nusselt number increase as the buoyancy parameter increases，while only the Nusselt number increases but the skin friction coefficient decreases as the Prandtl number increases.For opposing flow，both the skin friction coefficient and the Nusselt number decrease as the buoyancy parameter increases，but both increase as the Prandtl number increases.

exponentially stretching vertical sheet;stagnation－point flow;mixed convection;heat transfer;boundary layer

O351.2

A

10.7631/issn.1000－2243.2016.06.0807

1000－2243(2016)06－0807－06

2016－01－12

许晓勤(1981－)，讲师，博士研究生，主要从事计算流体力学的研究，m140210004@fzu.edu.cn

2012年度中央财政支持地方高校发展专项资金资助项目(闽教财［2012］788号)