一类算子方程边值问题的可解性

金启胜

(安庆职业技术学院 公共基础部，安徽 安庆 246003)



一类算子方程边值问题的可解性

金启胜

(安庆职业技术学院 公共基础部，安徽 安庆 246003)

摘要：利用泛函的极小函数研究了一类算子方程边值问题的可解性，得到对称正算子方程有解的充分必要条件，以及泛函存在极小函数的充分条件。并对三种边值问题的实例进行了验证。

关键词：对称算子；正算子；正定算子；极小函数；Green第二公式

0引言

(1)

的线性定解问题。其中L,Lj是线性微分算子，f(x)是已知函数。

此线性定解问题对应于Hilbert空间H中一个线性算子方程Au=f(x)，其中A的定义域DA是H的一个线性稠密子集合。比如当H=L2(Ω)时，取

Au的值与Lu的值在DA上是相同的。故求解方程(1)就是在DA上求解方程：

Au=f(x)。

定义1对任意的u,v∈DA，如果算子A满足等式(Au,v)=(u,Av)，则称A为对称算子。

定义2设A是定义在Hilbert空间H的某一线性稠密子集DA上的线性算子，如果对DA中任意元素u，有(Au,u)≥0且等号成立时当且仅当u=0，则称A为正算子。

定义3设A是DA上线性算子，如果存在常数γ>0，对任意的u∈DA都有(Au,u)≥γ2(u,u)，则称A是DA上的正定算子。

在DA上引入新内积[u,v]=(Au,v)；和新内积对应的新范数记为：

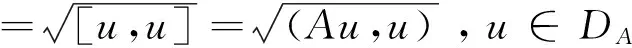
根据算子A的正定性可知，原空间H和新空间H*的范数满足：‖u‖‖u‖*。

2主要结论及证明

定理1 若A为正算子，则方程Au=f(x)至多有一个解u∈DA。

证明如果Au=f(x)有两个解u,v，则Au=f(x)，Av=f(x)。二式相减得：

A(u-v)=0，所以(A(u-v),u-v)=0，又A为正算子，所以u-v=0，即u=v。

定理2设A为对称正算子，若方程Au=f(x)有解u0∈DA，则u0必是泛函：

F(u)=(Au,u)-2(u,f)

(2)

的极小函数；反之，若u0∈DA是F(u)的极小函数，则有Au0=f(x)。

证明泛函F(u)和算子A的定义域相同。设Au0=f(x)，对任何v∈DA，v≠u0，令η=v-u0，因为DA是线性子集合，则η∈DA。根据算子A的对称性得：

F(v)=F(u0+η)=(A(u0+η),u0+η)-2(u0+η,f)，

=(Au0,u0)+2(Au0,η)+(Aη,η)-2(u0,f)-2(η,f)，

=F(u0)+2(Au0-f,η)+(Aη,η)=F(u0)+(Aη,η)>F(u0)。

所以u0必是泛函F(u)=(Au,u)-2(u,f)的极小函数。

反之，设u0∈DA是F(u)的极小函数，η∈DA，则u0+λη∈DA，λ∈R。当

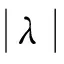
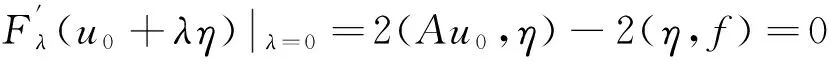
如果Au0-f∈DA，取η=Au0-f，所以Au0-f=0，即Au0=f(x)。

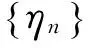
ηn→Au0-f在H中成立，于是由(Au0-f,ηn)=0得(Au0-f,Au0-f)=0，所以Au0=f(x)，即u0是算子方程Au=f(x)的解。

定理3若A为对称正定算子，则泛函F(u)在H*中存在极小函数。

∀u∈H*。

所以泛函F(u)在u=u0时取得极小值。

3应用举例

设Ω是Rm(m≥2)中有界区域，对于位势方程-Δu=f(x),x∈Ω，考虑三种边值问题的边界条件：

其中σ0是正常数，ν是∂Ω的单位外法向。求解这三类边值问题转化为求对应的泛函的极小函数问题。这就必须先验证各自对应的算子为对称正算子。取Hilbert空间为L2(Ω)。

(1)对应于Dirichlet问题的算子-Δ定义域为：

若u,v∈D1，由Green第二公式得：

所以-Δ是D1上的对称算子。另外，当u∈D1时，有：

当且仅当u恒等于常数时等号成立。由u的连续性及边界条件得在Ω上u≡0。所以-Δ是D1上的对称正算子。

(2)对于Neumann问题，不是对任何函数都是可解的。因为对方程-Δu=f(x),x∈Ω两边在Ω上积分，运用基本解公式及边界条件得：

另外，任何一个解加上一个常数后仍然是问题的解，为了保证解唯一就必须附加条件。比如所求解满足∫Ωudx=0，显然此时的解唯一。选择对应于Neumann问题的算子-Δ定义域为：

(3)对应于Robin问题的算子-Δ定义域为：

(-Δu,v)-(u,-Δv)=-∫Ω(vΔu-uΔv)dx，

所以-Δ是D3上的对称算子。另外，当u∈D3时，有：

(-Δu,u)=-∫ΩuΔudx，

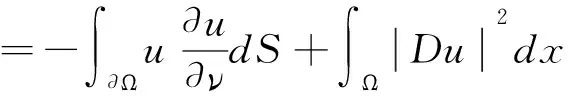
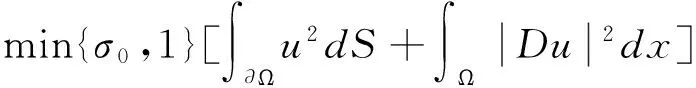
(-Δu,u)=0⟺u≡0，所以-Δ是D3上的对称正算子。

所以根据定理2得，(1)、(2)、(3)三问题的求解依次化为下列泛函：

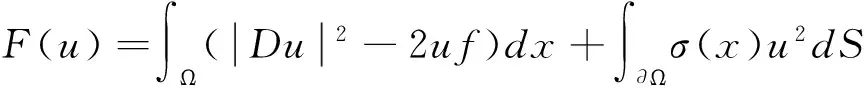
分别在集合D1，D2，D3上求极小函数问题。

最后，我们验证泛函的极小函数存在问题，即验证算子-Δ在对应的线性集合上是正定的。对于本文中提到的三种边值问题，我们只验证Robin问题的算子-Δ是D3上的正定算子。对于算子-Δ在D1，D2上是正定的可类似进行验证。

设区域Ω在第一象限，且完全含于闭域Ω1={0xa,0yb}之内。根据不等式(-Δu,u)

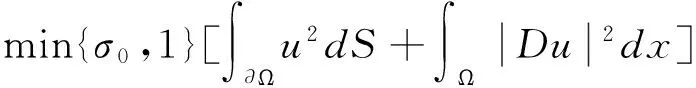
为此我们令u=gv，其中v是未知函数，g是待定函数。

≥-v2gΔg+(v2ggx)x+(v2ggy)y。

将上面不等式在Ω上积分，并且利用散度定理得到：

-∬Ωv2gΔgdxdy∬，即

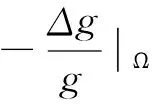
c1∬Ωu2dxdy∬，取，即得不等式

所以，算子-Δ是D3上的正定算子。

参考文献：

[1]陈祖墀.偏微分方程[M].合肥:中国科学技术大学出版社,2004.

[2]曾志芳,朱传喜.半序空间中三元算子方程的可解性问题的研究[J].系统科学与数学，2014,34(5):582-588.

[3]冯育强,刘三阳.半序空间中一类算子方程的可解性[J].数学学报，2003,46(2):411-416.

[4]姚福元.一类算子方程的可解性[J].科学通报，1991,36(11):804-806.

责任编辑：程艳艳

Solvability of Boundary Value Problem of a Class of Operator Equations

JIN Qisheng

(Department of Public Fundamental Courses, Anqing Vocational and Technical College, Anqing 246003, China)

Abstract：This paper discusses the solvability of boundary value problem of a class of operator equations by using the minimum function, getting the necessary and sufficient conditions for symmetric positive solutions to operator equations, as well as the sufficient condition for the existence of the minimum function in functions. And three kinds of boundary value problems are verified by examples.

Keywords：symmetric operator; positive operator; positive definite operator; minimum function; second formula of Green

收稿日期：2016-04-29

基金项目：2015年安徽省质量工程项目(2015jyxm539)；2016年安徽省自然科研项目(KJ2016A447)

作者简介：金启胜(1972-)，男，安徽桐城人，副教授，硕士，主要从事微分方程方面研究。

中图分类号：O175.2

文献标志码：A

文章编号：1009-3907(2016)06-0054-04