混沌优化神经网络求解job-shop调度问题研究

赵　莉， 齐耀武

(1.长春大学 机械与车辆工程学院，长春 130022；2.中东长春轨道客车股份有限公司 转向架制造中心，长春 130062)



混沌优化神经网络求解job-shop调度问题研究

赵莉1， 齐耀武2

(1.长春大学 机械与车辆工程学院，长春 130022；2.中东长春轨道客车股份有限公司 转向架制造中心，长春 130062)

摘要：针对Job Shop调度问题，建立了离散非线性回馈神经网络优化模型，给出了一种包含暂态混沌过程的神经网络优化方法。通过在优化神经网络中引入一个暂态的混沌过程，使得网络的演化具备更为灵活的动力学特征。网络状态轨迹随着自反馈系数的衰减，表现为一个典型的倍周期逆分叉过程，逐渐趋向于确定性的非线性回馈神经网络，并为其提供了一个接近全局最优点的初值。其实质是利用混沌搜索过程的随机性和状态遍历性，加强神经网络的全局优化能力，避免陷入局部极小点。仿真结果说明本文所建模型和优化方法比传统的非线性神经网络优化方法具有更好的收敛性和更高优化能力。

关键词：Job Shop调度；神经网络优化；混沌优化

0引言

Job-shop(JSP)调度问题是按照一定的时间顺序要求分配资源完成加工任务的生产调度问题，是生产过程中经常遇见的问题。研究已证明它是NP困难问题[1，2]。显然对于此类问题的研究和解决，既具有理论意义，也具有实用价值。在当今研究中，解决此类调度问题的主要方法可分为四类：仿真技术法[3]、组合优化方法[4]、人工智能方法[5]和智能优化方法[6，8]。回馈神经网络优化是智能优化方法中应用较为广泛的方法之一，主要包括Hopfild线性回馈神经网络方法和非线性回馈神经网络方法[9]。

FooS.Y.P.和Y.Takefuji最早提出将神经网络用于求解JSP问题，并给出基于Hopfield神经网络的JSP优化方法。他们通过建立工序交换矩阵和决策成本树将JSP问题转换为TSP类型的组合优化问题，并利用玻尔兹曼机和模拟退火方法进行优化求解。在此基础之上，又有许多学者对其进行研究并扩展和完善了该方法[10-13]。然而此类方法在建模时采用了过多数量的神经元节点，以nxm规模的JSP问题为例其需要建立nm×mn+nm个神经元节点，这使得其难以应用于大规模问题优化。鉴于此，Zhou D.N.等人提出了求解此类问题的非线性回馈神经网络优化方法[6]。该方法针对任务时间状态变量建模，对于nxm规模的问题只需建立n×m个神经元节点；并采用梯度搜索进行优化求解。显然该方法建模复杂度低，更适于进行大规模问题的优化求解。然而该方法在求解过程中，搜索难以保证状态轨迹的全局遍历性，简单的梯度搜索使其非常容易陷入局部极小，甚至导致结果收敛于不可行解，最终影响该方法的优化性能。

为此，本文提出基于混沌神经网络的JSP优化调度方法。该方法利用非线性回馈神经网络建立JSP调度问题模型，通过对模型中的神经元增加自反馈，使神经元网络中形成一暂态时变的倍周期逆分叉过程，并利用混沌动力系统的全局遍历性避免神经元网络陷入局部最优点，达到增强算法的全局优化能力的目的。仿真实验表明，该方法在计算时间和收敛性都有效地提高了原有的非线性回馈神经网络方法。

1暂态混沌神经网络JSP调度问题建模

1.1JSP问题描述

JSP调度问题是服从分配和队列限制的资源分配问题，需要在设备资源上进行加工的工件叫做任务；工件在某台设备上的加工叫做一道工序或是一个子任务，每个工作是由多道工序或多个子任务组成的，这些工序之间具有先后次序的限制和要求。假设用I={1,2,…,n}代表工作集，用Ki={1,2,…ki}表示工作i的任务集或工序集，Sik表示工作i的第k道工序的开工时间，m(i,k)表示工作i的第k道工序在设备m(i,k)上进行加工，加工时间为ti,k。则JSP调度问题就是满足下列约束条件的某种准则的优化问题：

(1)

Si1≥0, 1in;

(2)

(3)

其中式(1)表示任何工作的后一工序的加工起始时间一定要大于或等于前一工序的加工结束时间，式(2)表示每一工作的首工序加工起始时间要大于或等于零；式(3)表示在同一设备上加工的两个工序m(i,k)=m(j,p)，或者工序(i,k)在工序(j,p)前面加工，或者工序(j,p)在工序(i,k)前面加工。在上述约束条件下，根据不同的优化准则可以得到不同JSP调度问题。本文将以所有工作最后一道工序开始时间总和最小为准备，即JSP问题的目标函数为：

(4)

1.2暂态混沌神经网络JSP调度问题建模

对一n个工作m台设备的JSP调度问题，可建立一包含n×m个神经元的优化系统，神经元的输出为工序(i,k)的起始加工时间Si,k，系统输出状态集为S=(s11,s12,...,snkn)。与Hopfield神经网络类似，非线性回馈网络神经元(i,k)的动态方程和网络的能量函数可分别描述为：

(5)

(6)

其中，uik是神经元(i,k)的内部状态，且sik=g(uik)，g(u)是u的单调递增函数，fik(s)是神经元(i,k)的输入量，是关于系统输出状态集S的非线性函数，C,R分别为容抗和阻抗参数。

根据神经网络优化的罚函数方法，可将JSP调度问题的目标函数描述为：

其中，A，B，C和D均为系统参数。当x>0时令F1(x)=ebx-bx，F2(x)=ebx-1，否则令F1(x)=F2(x)=0。

令E=I，并对等式两边对sik微分可得，

(7)

其中

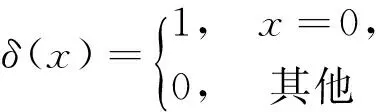
建立非线性回馈神经网络，并令神经元的输入fik(s)如(7)式所示，则当所建立的非线性神经网络能量达到平衡时，系统输出即为调度问题的优化结果。

前文已指出由(7)式所建立的神经网络在搜索过程中容易陷入局部极小，甚至导致结果收敛于不可行解。为此，在同步更新模式下，对上述神经网络进行Eular离散化，

uik_new=α·uik(t)-β·(1+η·zik(t))·fik(s)-zik·(η·sik-s0)

(8)

uik=uik_new

(9)

(10)

(11)

zik_new=H1·γ1·zik(t)+(1-H1)·γ2·zik(t)

(12)

zik=zik_new

(13)

其中，

α是阻尼因子，β是输入增益系数，0<γ2<γ1<1为衰减系数，z<λ为自反馈控制参数，s0为自反馈偏置参量，ω为输出比例系数，H1为自适应控制参数，其余皆为系统常数。(8)式为在每一神经元新增一较大反馈后的动态方程，(11)式是(7)式的延伸，是为了保证在同一加工任务的前后工序发生时序冲突时约束传播的双向性。

在上述神经网络模型中，该神经网络实质上是由能在状态空间表现出混沌行为的神经元耦合而成的，其基本动力学方程可以描述为：

uik(t+1)=α·uik(t)-zik(t)·(sik(t)-s0)

其中zik(t)·(sik(t)-s0)是神经元的自抑制反馈项，当自反馈系数z增加到一定阶段时，系统的动力学过程即呈现出混沌现象。其动态过程如图1所示。

这种混沌现象具体表现为状态值动态递推过程的随机性和混沌遍历性。利用状态轨迹的随机性可以保证大范围的搜索能力，利用状态轨迹的混沌遍历性则可以保证系统安动力学方程不重复的遍历所有可能状态，同时与梯度搜索过程结合，使得神经网络可以有效的避免局部最小点，收敛至全局最优解。

考察神经元动态方程：

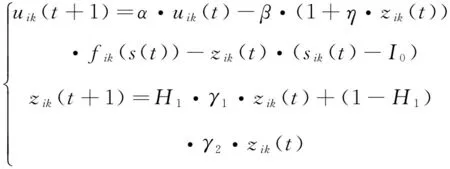
为避免初始反馈增益过大，导致状态收敛至混沌过程的固有不动点，对影响梯度搜索的输入增益系数β采用自适应控制，令β′=β·(1+η·z)，即在混沌状态采用高增益系数，随者z不断衰减，系统脱离混沌，β也变化为正常设定值，转入梯度搜索。

2仿真实验

为分析混沌神经网络优化过程中的非线性动力学特性，对n=4,m=3的JSP调度问题进行仿真，系统参数如表1、表2所示。

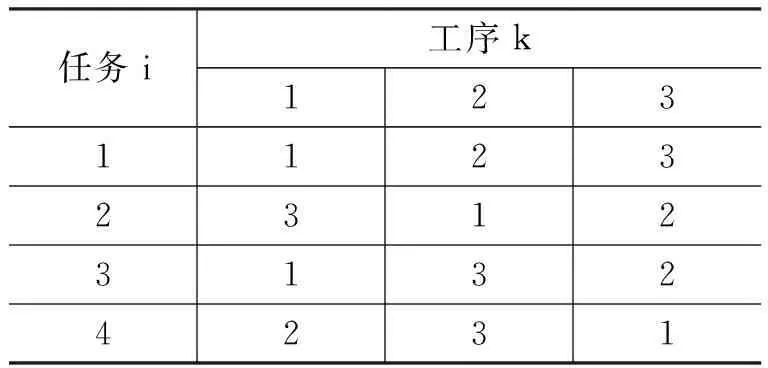
表1　工序分配表m(i,k)

表2工序时间表

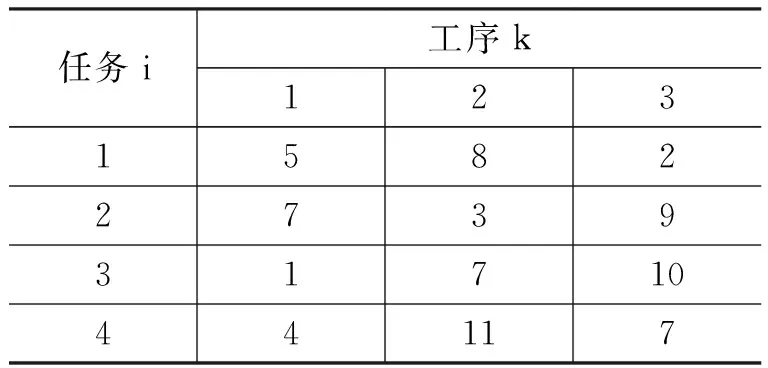
任务i工序k123158227393171044117

适当调整系统初始状态值U(0)，当系统收敛时，可以得到经优化的各工序起始加工时间sik如表3所示，系统甘特图如图3所示。

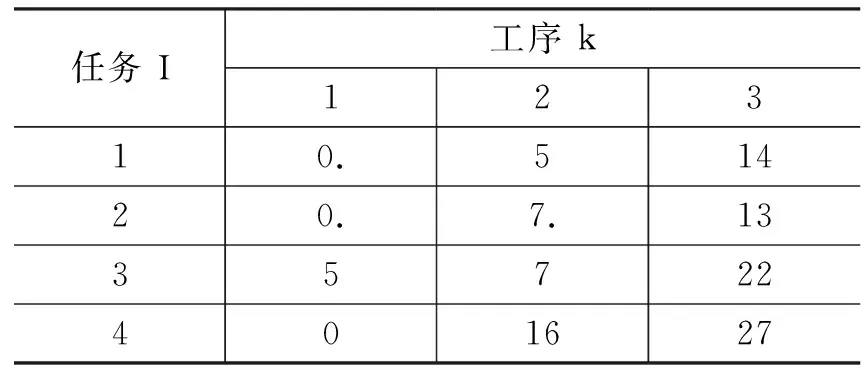
表3　工序起始加工时间sik

由系统运行轨迹图可看出，在搜索开始阶段控制参数z较大，自抑制反馈很强，系统进入混沌搜索过程，输出状态与系统内部状态轨迹呈现出随机性与状态遍历性。此后控制参数z转而进入时变衰减，混沌轨迹表现为一个倍周期逆分叉的收敛轨迹，混沌现象逐渐消失，系统恢复为梯度搜索，直至得到最后结果。

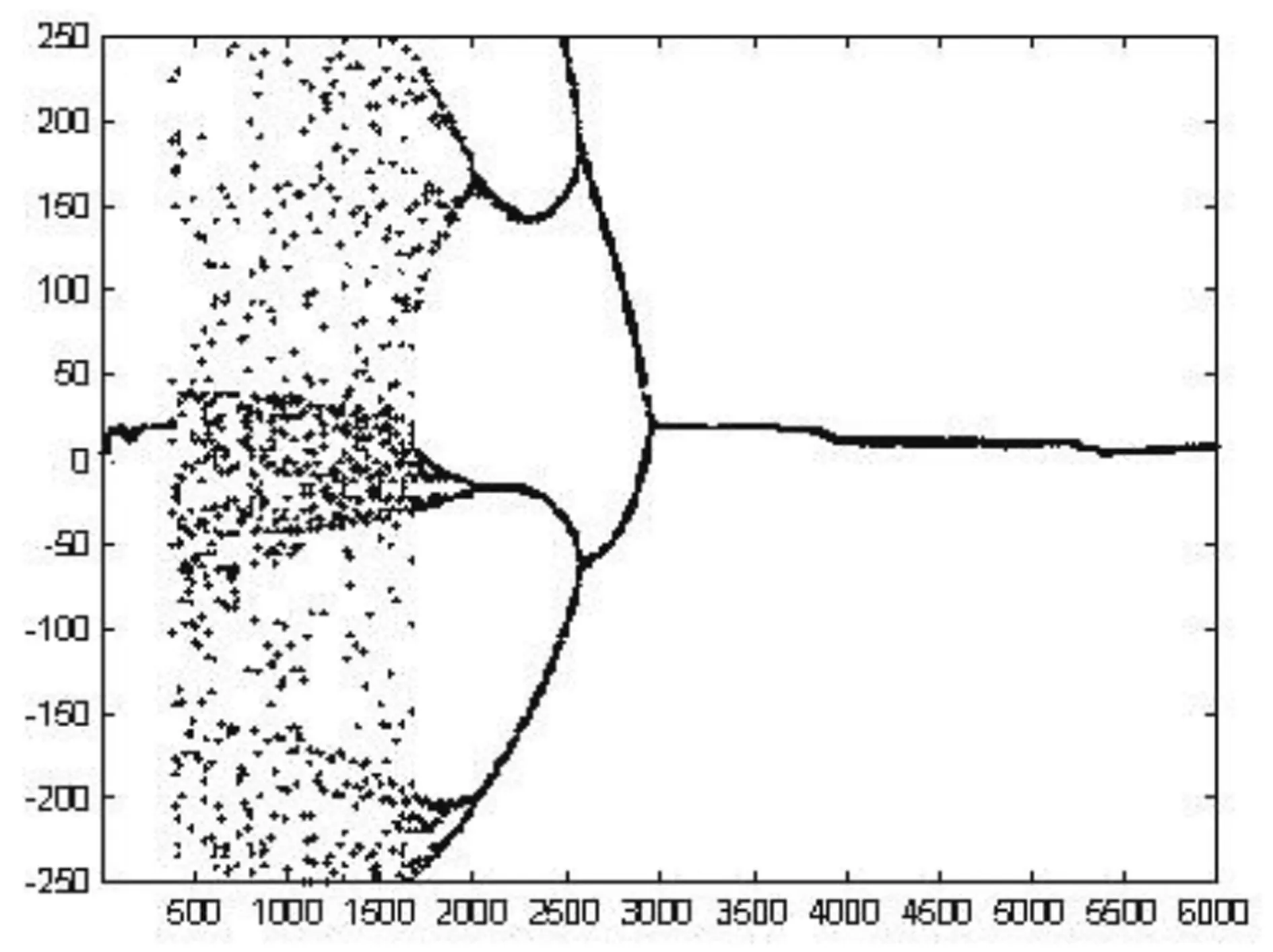
图1(a)系统的动力学过程样力1图

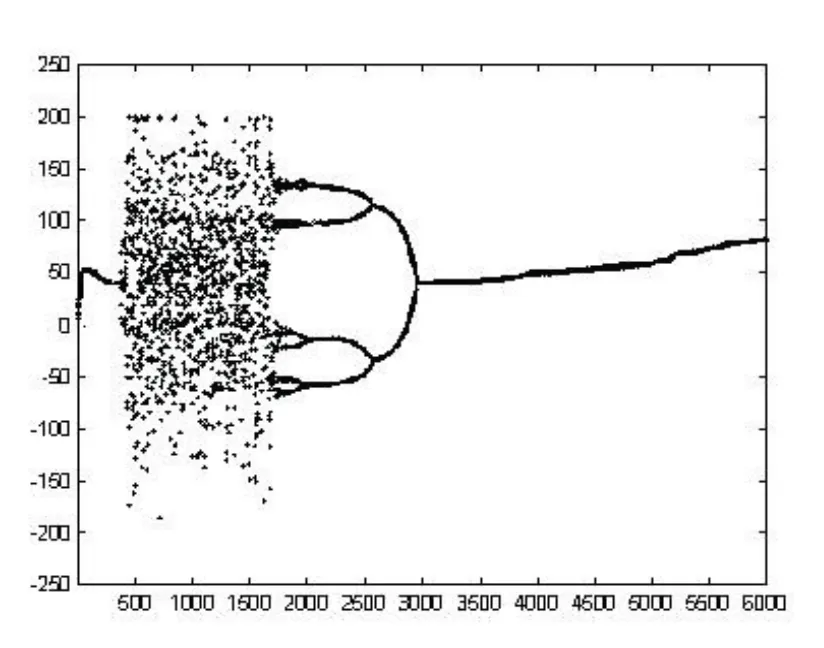
图1(b)系统的动力学过程样力2图

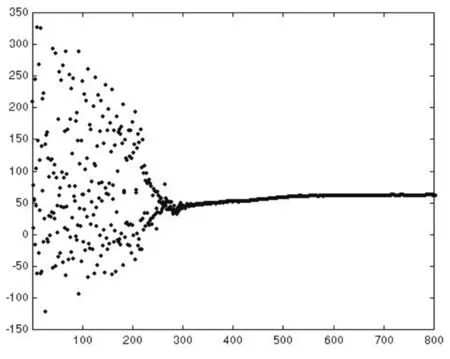
图2(a) uik动力学轨迹图

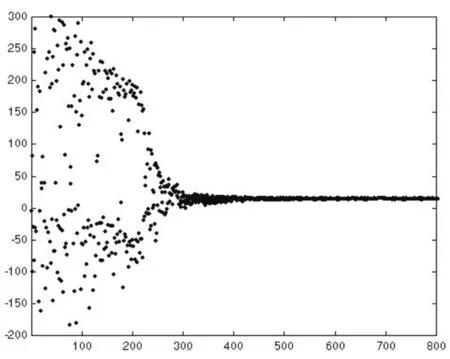
图2(b) uik动力学轨迹图

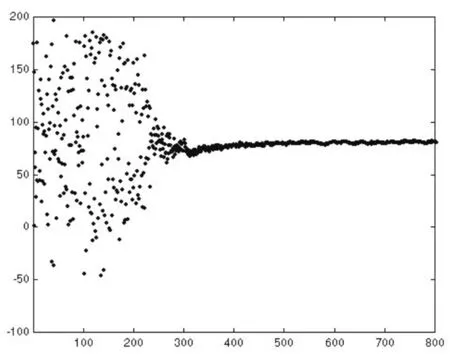
图2(c)目标函数Siki的动力学轨迹图

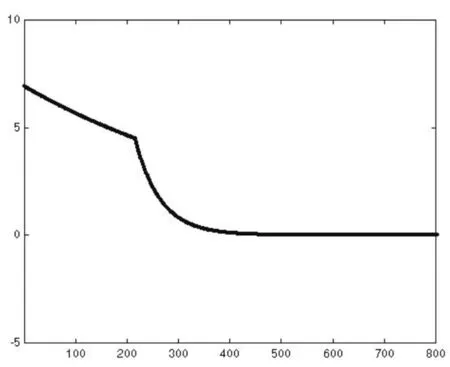
图2(d)自反馈控制参数z的动态轨迹图

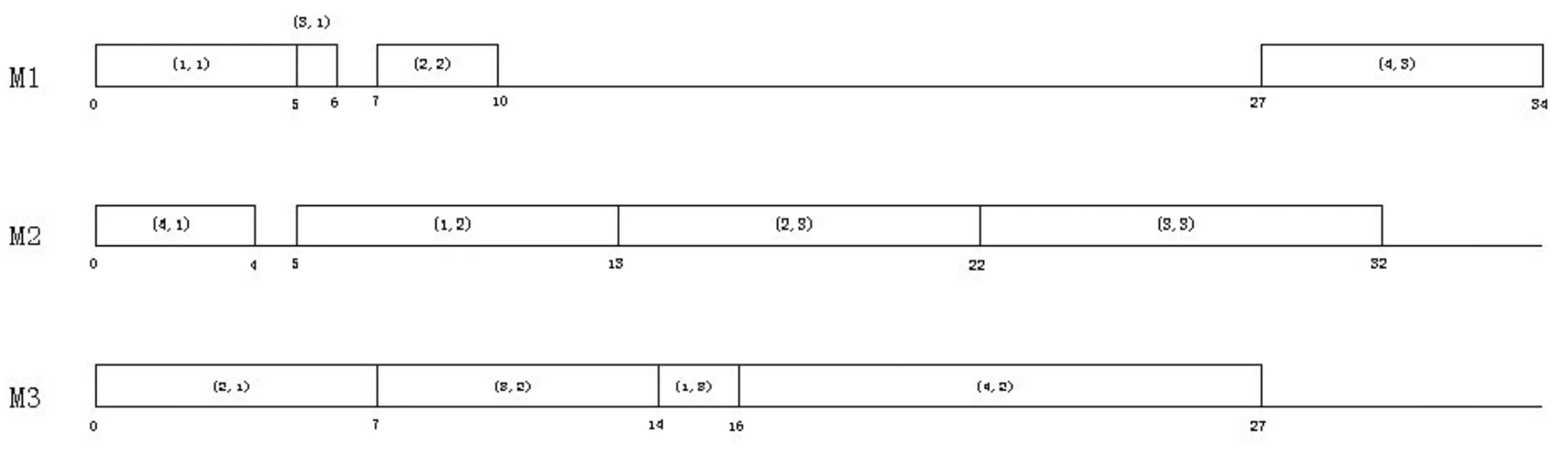
图3　系统甘特图

在区间[0,5]上选取两初始状态值U′(0)和U″(0)，在相同条件下对暂态混沌神经网络和非线性回馈神经网络分别进行优化，定义满意解为与最优解相差小于5%，其输出优化结果分别如图4(a)，(b)，(c)和(d)所示。

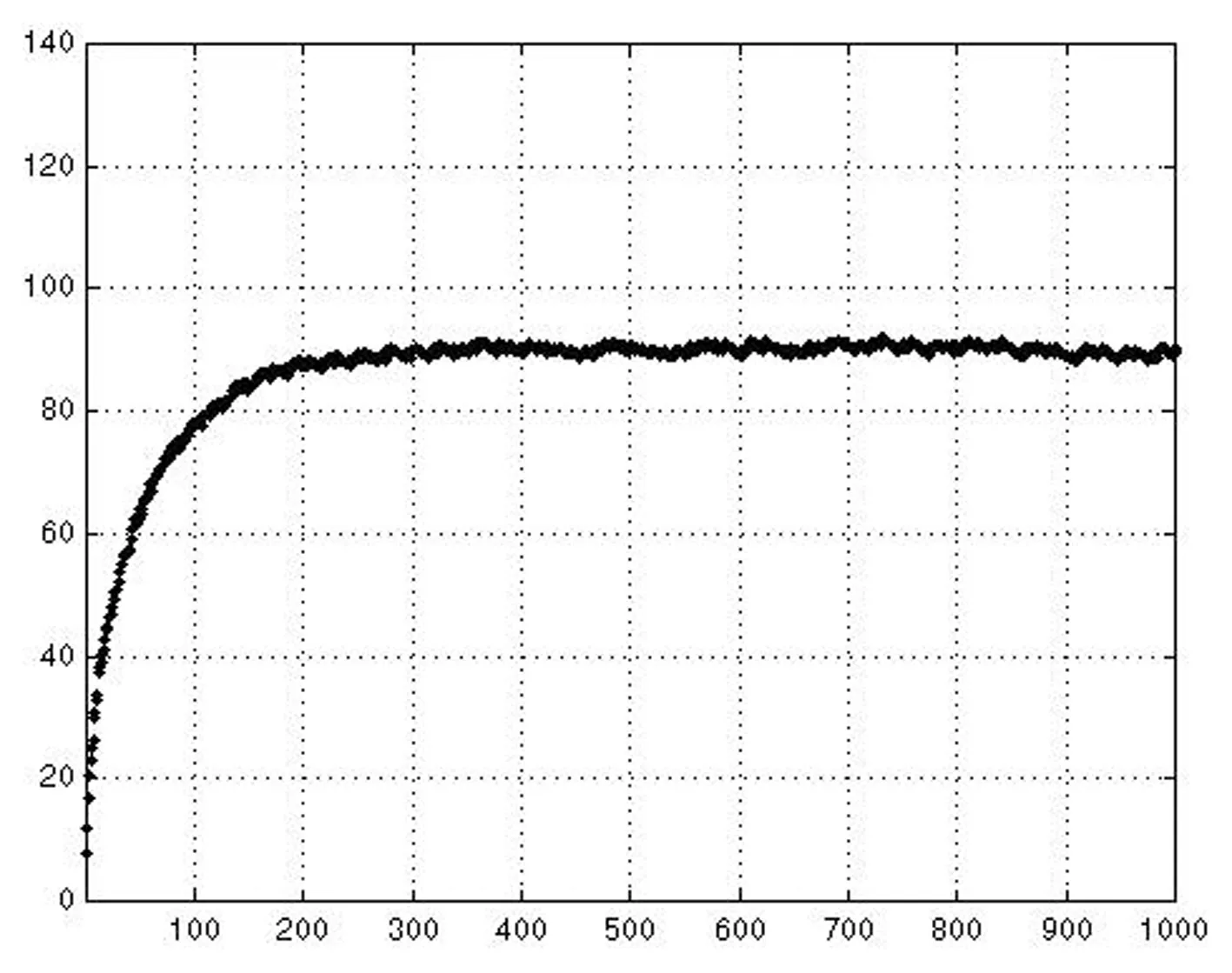
图4(a)初始状态值U′(0)非线性回馈神经网络优化结果输出图

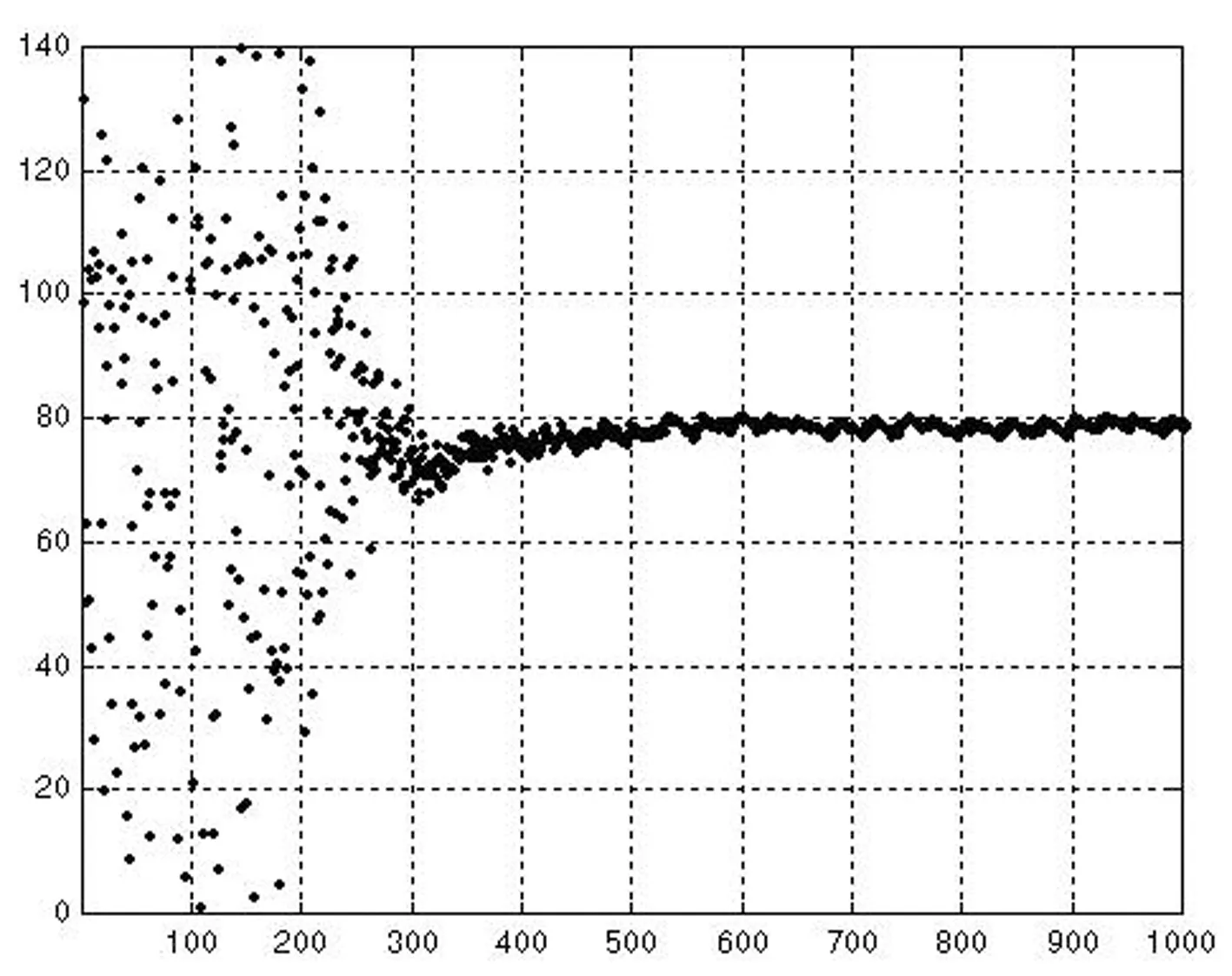
图4(b)初始状态值U′(0) 暂态混沌神经网络优化结果输出图

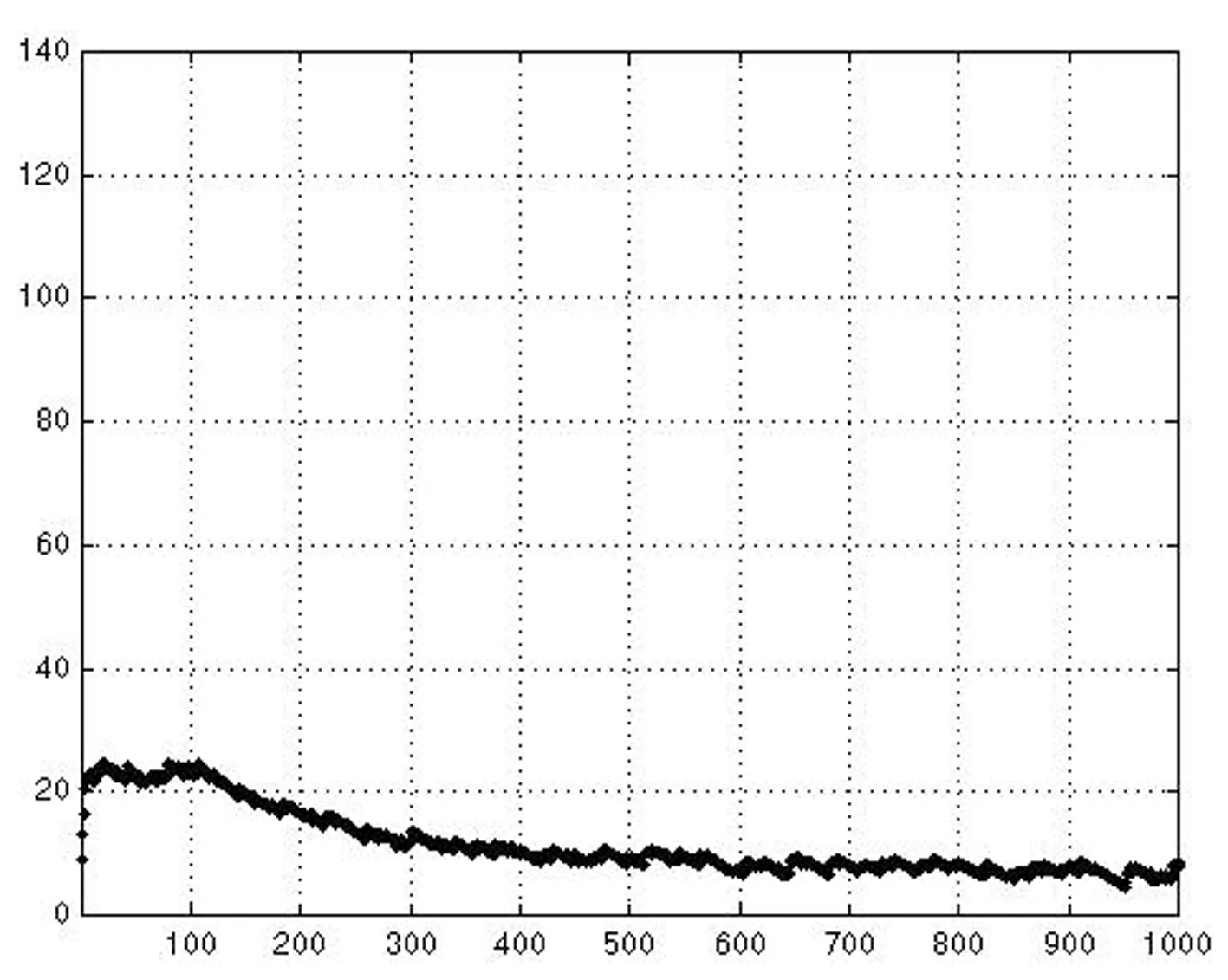
图4(c)初始状态值U″(0) 非线性回馈神经网络优化结果输出图

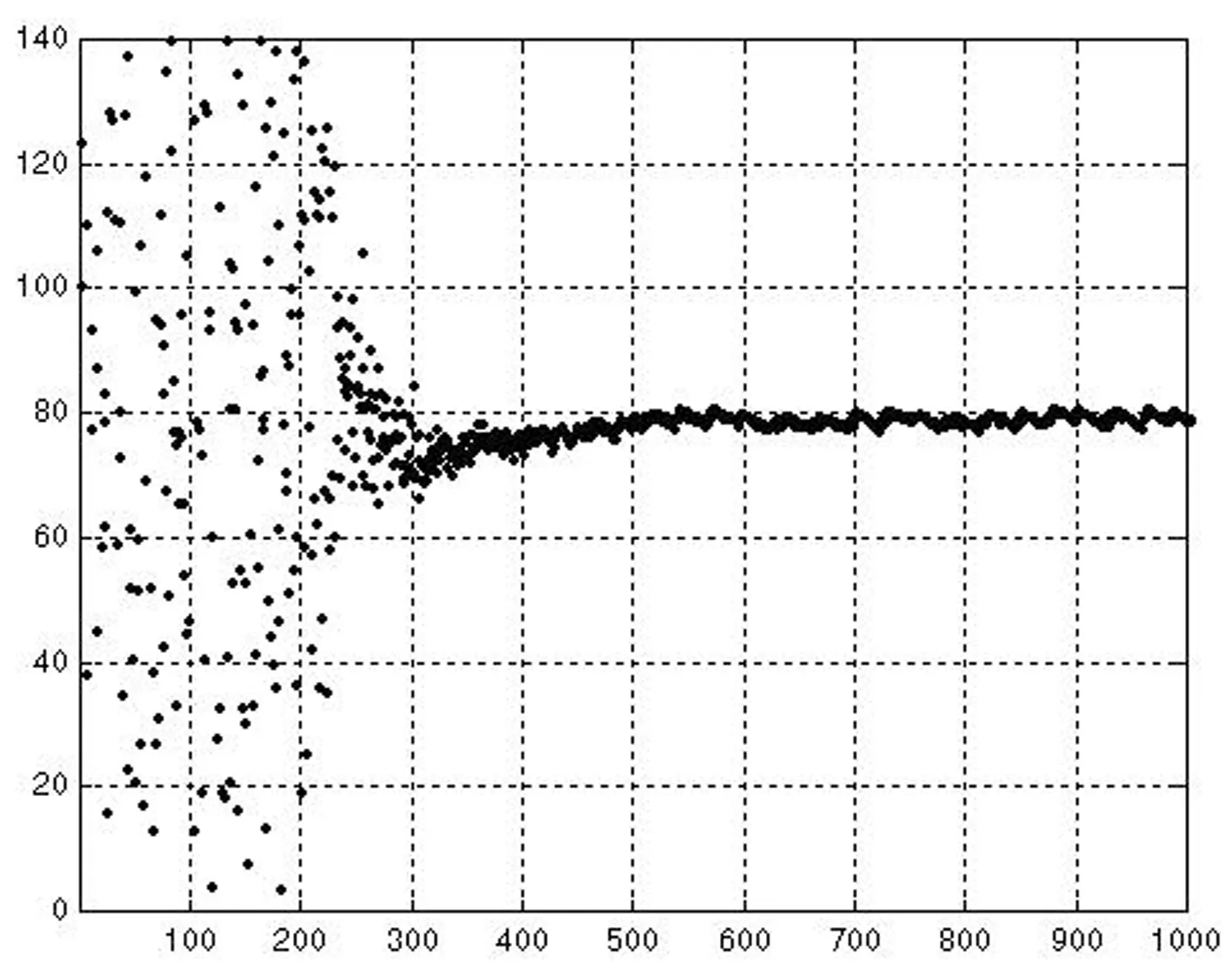
图4(d)初始状态值U″(0)暂态混沌神经网络优化结果输出图

通过上述结果可以看出，在初始状态条件下，一般非线性回馈神经网络一次收敛于一般有效解，一次收敛于非法解，而暂态混沌神经网络则均收敛于满意解，优化效果明显好于前者。此外，再分别对普通非线性回馈网络与混沌神经网络进行200次优化仿真，其优化结果如下。

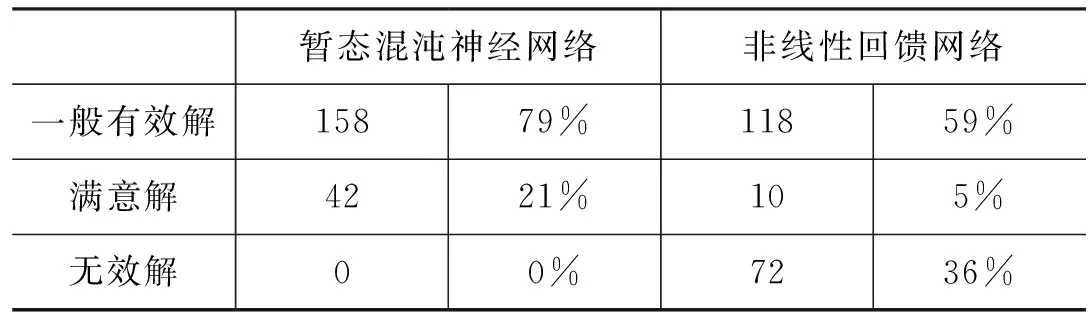
表4　优化性能比较

由上述仿真结果可以看出，增加了暂态混沌过程的神经网络，由于混沌过程的随机性和混沌遍历性，使得神经网络系统一方面具备大范围的搜索能力，系统状态可以安动力学方程不重复的遍历多种可能状态，有效避免能量函数的局部最小点，另一方面可以也减弱系统的初值敏感性，减少系统由于状态初值选择不恰当而收敛至不可行解的可能性。上述仿真实验结果对此给出了很好的验证。

3结论

本文针对JSP调度问题，给出了一种包含暂态混沌过程的非线性回馈神经网络优化方法。通过引入一个暂态的混沌过程，使得神经网络的演化具备更为灵活的动力学特征。随着自反馈系数的不断衰减，网络状态轨迹表现为一个倍周期逆分叉过程，并逐渐趋向于确定性的非线性回馈神经网络，并为其提供了一个接近全局最优点的初值。其实质是利用混沌搜索过程的随机性和状态遍历性，加强神经网络的全局优化能力，避免陷入局部极小点。仿真结果说明了本文所建模型和优化方法的有效性。

参考文献：

[1]Foosy Takefujuy.Stochastic neural networks for solving job-shop scheduling: Parts I problem representation [C].Proceeding of the IEEE International Conference on Neural Networks,1988,275-282.

[2]Foosy Takefujuy. Stochastic neural networks for solving job-shop scheduling:Parts II .Architecture and simulations [C].Proceeding of the IEEE International Conference on Neural Networks,1988.283-290.

[3]Kiran Allen,Simth,Williamas.Job-Shop调度中的仿真研究[C].郑彦译，计算机集成制造系统译文集，北京：中国科学院自动化研究所，1988.

[4]Alan Smith Manne, On the Job-Shop Scheduling Problem [J]. Operations Research,1959,7(2):123-132.

[5]Eseale.Benaana,Gucci.Bel and David.Dubois.OPAL:A multi knowledge-based system for industrial job-shop scheduling [J].International Journal Production Research,1988,26(5):795-819.

[6]刘民，孙元凯，吴澄.TS+BS混合算法及其在job-shop调度问题上的应用[J].清华大学学报，2002,42(3):424-426.

[7]潘全科，王文宏，朱剑英.基于粒子群优化和模拟退火的混合调度算法[J].中国机械工程，2006(10):953-957.

[8]韩世芬.基于模拟退火算法的Job Shop问题研究[J].电脑与电信，2007(7):612-615.

[9]朱颢.基于智能优化算法的Job Shop调度问题的研究[D].天津：天津大学，2004.

[10]Zhou Deming,Charkassky Vladimir,Baldwin Tred.et al.Scaling neural network for job-shop scheduling [A].Proceedings IEEE International Joint Conference on Neural Networks[C].1989.889-894.

[11]Willems Thomas, Brandts Lem. Implementing heuristics as an optimization criterion in neural net works for job shop scheduling[J]. Journal of Intelligent Manufacturing, 1995; 6(2): 377-387.

[12]Chang Shui Zhang, Ping Fan Yan, Chang Tong. Solving job-shop scheduling problem with priority using neural net work [C]. Proceedings IEEE International Joint Conference on Neural Networks，1991，1361-1366.

[13]张长水,阎平凡.解Job-shop调度问题的神经网络方法[J].自动化学报, 1995, 21(6 ):706-712.

责任编辑：程艳艳

Research on a Solution to Job-shop Schedule Problems by Neural Network with Chaotic Optimization

ZHAO Li， QI Yaowu2

(1.College of Machinery and Vehicle Engineering, Changchun University, Changchun 130022, China；2.Bogie Manufacture Center,CRRC Changchun Railway Vehicles Co., Ltd., Changchun 130062, China)

Abstract：In view of Job-shop schedule problems, an optimized model of disperse nonlinear feedback neural network is established, and a neural network optimization method with transient chaos is given, which introduces a process of transient chaos to an optimized neural network, making its evolution have flexible dynamics features. With the reduction of self-feedback coefficient, the state trajectory is shown as a typical inverse bifurcation process, converging to a definite nonlinear feedback neural network and providing a globally near-optimal solution. The essence is to improve the global optimization ability by the randomness and ergodicity of chaos searching, so as to avoid sticking into the local minima. Simulation results indicate that the established model and optimized method have better convergence and higher optimization ability than the traditional nonlinear neural network optimization method.

Keywords：Job-shop schedule; neural network optimization; chaos optimization

收稿日期：2016-04

基金项目：吉林省计算与软件科学创新平台基金资助(60374061)

作者简介：赵莉(1972-)，女，吉林长春人，副教授，硕士，主要从事工业工程及计算机应用方面研究。

中图分类号：TP18TP301

文献标志码：A

文章编号：1009-3907(2016)06-0006-07