基于反演的高超声速飞行器动态面滑模控制

谭诗利 王 洁 王鹏飞

空军工程大学，西安 710051



基于反演的高超声速飞行器动态面滑模控制

谭诗利 王 洁 王鹏飞

空军工程大学，西安 710051

针对高超声速飞行器纵向平面轨迹跟踪问题，提出一种基于反演的动态面滑模控制方法。引入一阶滤波器以避免传统反演控制的“微分项膨胀”问题，利用双曲正切函数的平滑特性以减弱抖振，设计自适应估计律，对干扰项在线估计以增强鲁棒性。仿真结果表明，该方法对高度和速度控制指令具备良好的跟踪性能。 关键词 高超声速飞行器；滑模控制；动态面控制；反演控制；滤波器

高超声速飞行器在民用和军事领域有重要的应用前景，已成为各国研究的热点。相比常规飞行器，高超声速飞行器模型更复杂，具有显著的非线性特性，且存在严重的结构弹性和热弹性效应，模型不确定性增加[1]。这些特征给控制器的设计带来了全新挑战。

反演方法解决了高阶非线性系统控制器设计复杂的难题，已被广泛运用到高超声速飞行器的控制中[2-4]。但单纯的反演在解决高阶系统的控制问题时易产生“微分膨胀”，且存在鲁棒性不强的缺点。动态面作为传统反演的补充，有效解决了“微分膨胀”问题且取得了很好的控制效果[5-6]。动态面控制方法可以避免高阶求导引起系统发散的问题，并能减小计算量[7]。滑模控制无需参数辨识且具备较强的鲁棒性，文献[8]使用Terminal滑模用于解决高超声速飞行器控制问题，文献[9]设计了自适应滑模控制器，增强了控制系统的鲁棒性。

本文针对高超声速飞行器纵向平面控制问题，首先给出面向控制模型，并分析其不确定项；然后结合反演和滑模控制方法设计控制器，设计动态面用于避免 “微分膨胀”，设计自适应估计律对干扰进行估计增强鲁棒性；最后，仿真验证了闭环控制系统的稳定性和动态性能。

1 高超声速飞行器模型

纵向平面的高超声速飞行器控制主要任务是通过控制输入量u=[Φδe]T(分别表示燃料当量比和升降舵偏角)来实现对参考值yref=[Vrefhref]T的快速稳定跟踪。国内外高超声速飞行器研究领域最常用的模型是由Bolender和Doman提出的弹性体模型[10]：

(1)

式中：V和h分别为飞行高度和速度；γ和α分别为航迹角和迎角；Q为俯仰角速度；ηi为弹性状态量；μ为万有引力常数；zT为推力相对于质心的力臂；m和Iy分别为飞行器质量及其沿y轴的转动惯量；ζi和ωi分别为阻尼比和自然振动频率；L，D，T及M分别为飞行器的升力、阻力、推力及俯仰力矩；Re为地球半径；Ni为广义弹性力。

式(1)所示的模型不仅含刚体状态量X=[V,h,γ,α,Q]T，还含弹性状态量，能逼真地反应系统的工作原理，但式(1)结构复杂，参数、变量多，方程阶次高，且方程形式复杂，直接用于控制器的设计不可行。针对这一情况，将式(1)中飞行器的升力L、阻力D、推力T及俯仰力矩M,广义弹性力Ni拟合成如下形式[11]：

(2)

将式(2)拟合的作用力或力矩代入飞行器的动力学方程式(1)中，推导出面向控制的严格反馈形式模型，如式(3)～(7)所示：

(3)

(4)

(5)

(6)

(7)

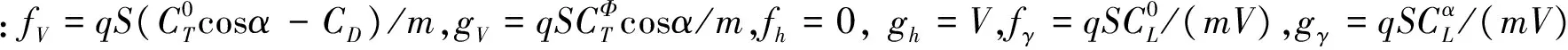
在式(3)～(7)中，di(i=V,h,γ,α,Q)为因式(2)中曲线拟合而引入的误差。令θi∈{θTθLθDθM}分别为推力、升力、阻力和俯仰力矩的拟合误差，θh为Tsinα和Vsinγ的近似误差系数，则

dV=(θTcosα-θD)/m，

dh=θhVγ2/2，

dγ=(θL+θTsinα)/mV，

dα=-dγ，

dQ=(zTθT+θM)/Iy。

在如式(3)～(7)所示的面向控制模型中，只含有刚体状态量X=[V,h,γ,α,Q]T，这是由于弹性状态量η在工程实践中无法测量，因此将弹性振动对刚体运动的影响计入拟合误差，这符合所设计控制器的工程实用性要求，并且如果设计的控制器具有鲁棒性，就能稳定弹性振动对飞行器刚体运动产生的影响。

综上，式(1)所示模型作为第4节仿真验证时的对象模型，用于验证所设计控制器的有效性。式(3)～(7)所示模型则用于第2节中控制器的具体设计。

2 控制器设计

2.1 速度控制器设计

速度由式(3)所示的一阶系统决定，速度V的大小主要受燃料当量比Φ的控制。基于滑模控制的设计思想，定义滑模面σV=V-Vref，则有

(8)

设计控制量Φ为

(9)

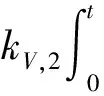
2.2 高度控制器设计

高度由式(4)～(7)组成的四阶系统决定，升降舵偏角δe引起俯仰角速度Q的变化，进而引起攻角α的变化，及航迹角γ的变化，最后引起高度h的变化。基于反演设计的思想，δe为实际控制量，定义Qc，αc和γc为虚拟控制量，定义滑模面：

(10)

实际控制量和虚拟控制量设计为

(11)

定义一阶滤波器动态系统的估计误差为：

(12)

(13)

(14)

一阶滤波器设计如下：

(15)

(16)

(17)

式中，τγ，τα，τQ为时间常数。

2.3 干扰上界估计

(18)

(19)

(20)

(21)

(22)

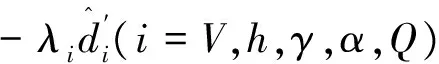
3 稳定性分析

首先定义不确定项的估计误差为

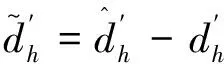
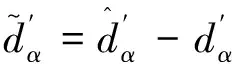
(23)

选取Lyapunov函数

W=WV+Wh+Wγ+Wα+WQ

(24)

其中，

(25)

(26)

(27)

(28)

(29)

运用Lyapunov函数证明稳定性时，使用了2个引理：引理1和引理2。

引理1 对于任意和任意常数，有如下不等关系式成立，

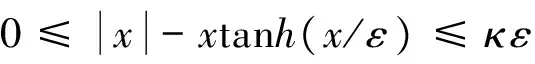
(30)

其中，κ为常数，满足κ=exp[-(κ+1)]，即κ≈0.2785。

引理2young′s基本不等式

±2xy≤cx2+(1/c)y2

(31)

其中，c>0为常数。

(32)

其中，ch,1，ch,2，cγ，cα,1和cQ,1为由Young’s基本不等式产生的常数，Δ取值如下：

(33)

4 仿真验证

飞行器在动压q=90148Pa，高度h=26212.8 m(86000ft)的初始巡航条件下，考虑典型的机动飞行情况：保持动压不变，高度指令的阶跃幅值为Δhc=1828.8m (6000ft)。将Δhc通过阻尼比ζn=0.95和自然频率wn=0.03rad/s的二阶参考模型环节，生成待跟踪的高度参考轨迹href(t)。仿真采用四阶Runge-Kuta数值求解，步长为0.001s。控制器的参数分别取值为：kV,1=2，kV,2=1.2,kh,1=1.5,kh,2=0.5,kγ,1=1.5,kγ,2=1,kα,1=2,kα,2=1.2,kQ,1=1.5,kQ,2=0.5,εi=0.01(i=h,γ,α,Q)，滤波器参数分别为τα=τγ=τQ=0.1，自适应估计律的参数为βi=0.1,λi=10 (i=h,γ,α,Q)。仿真结果如图1～6所示。

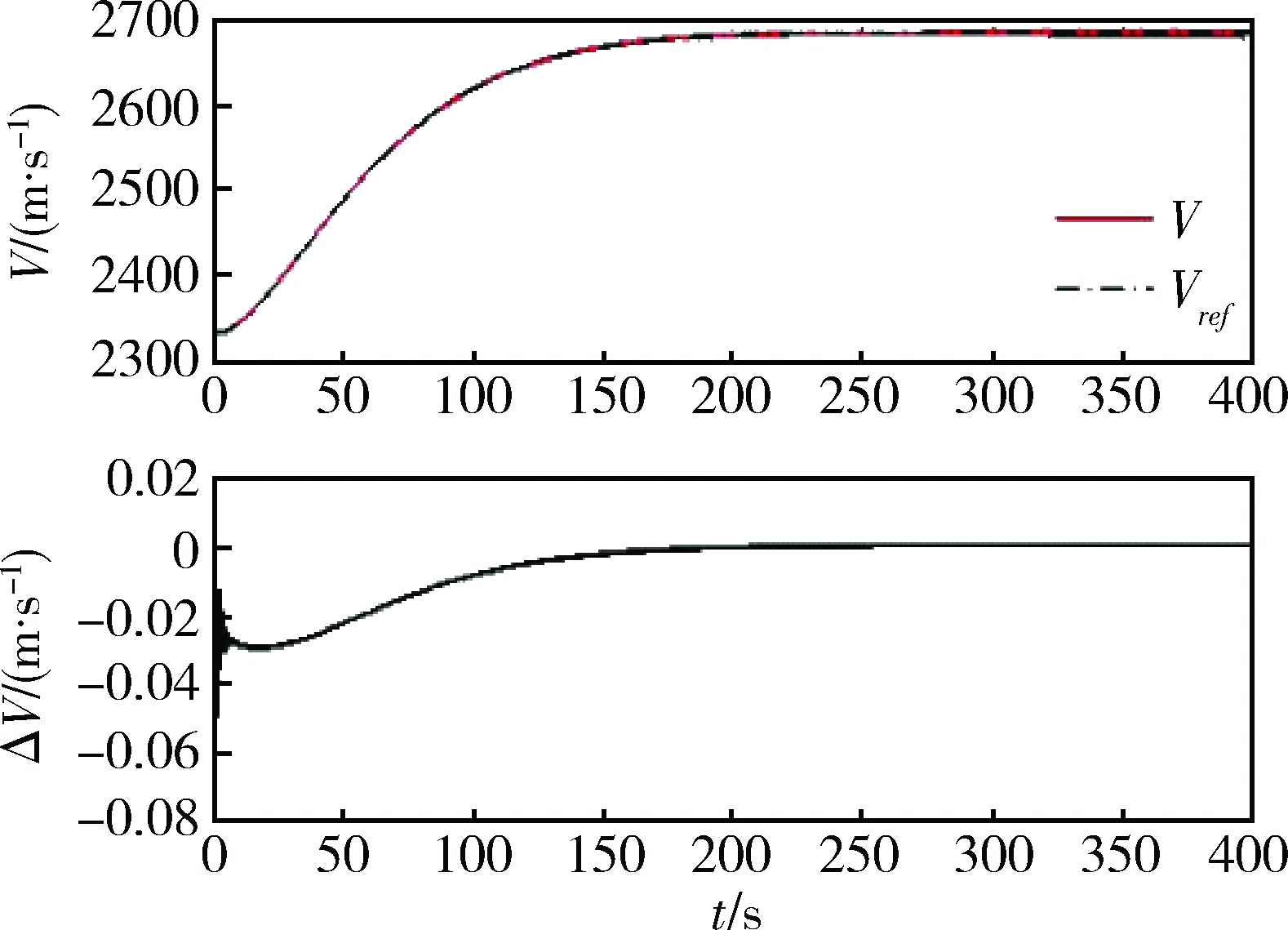
图1 速度跟踪及跟踪误差曲线

图2 高度跟踪及跟踪误差曲线

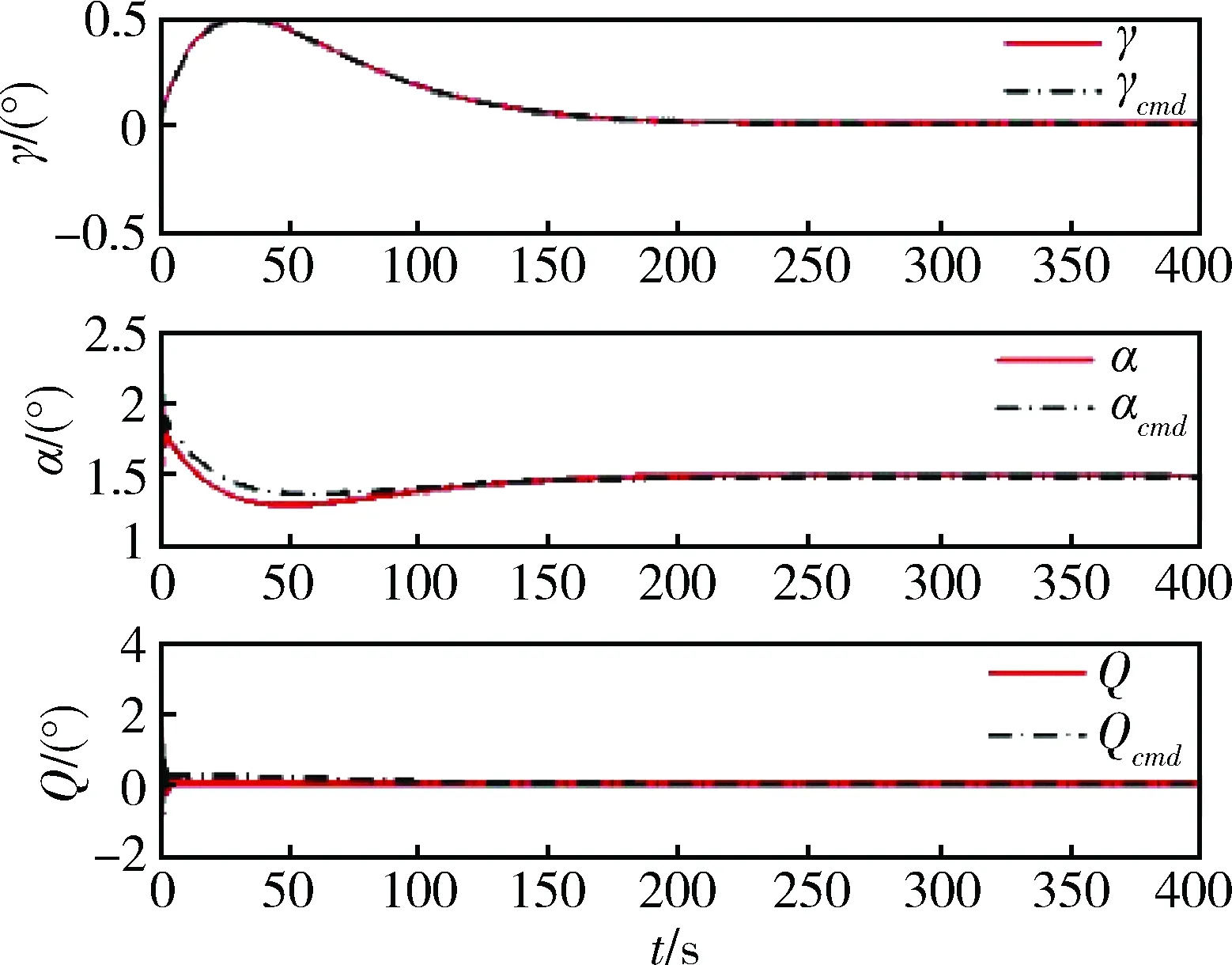
图3 航迹角、攻角和俯仰角跟踪曲线

图4 燃料当量比输入曲线

图5 升降舵偏角输入曲线

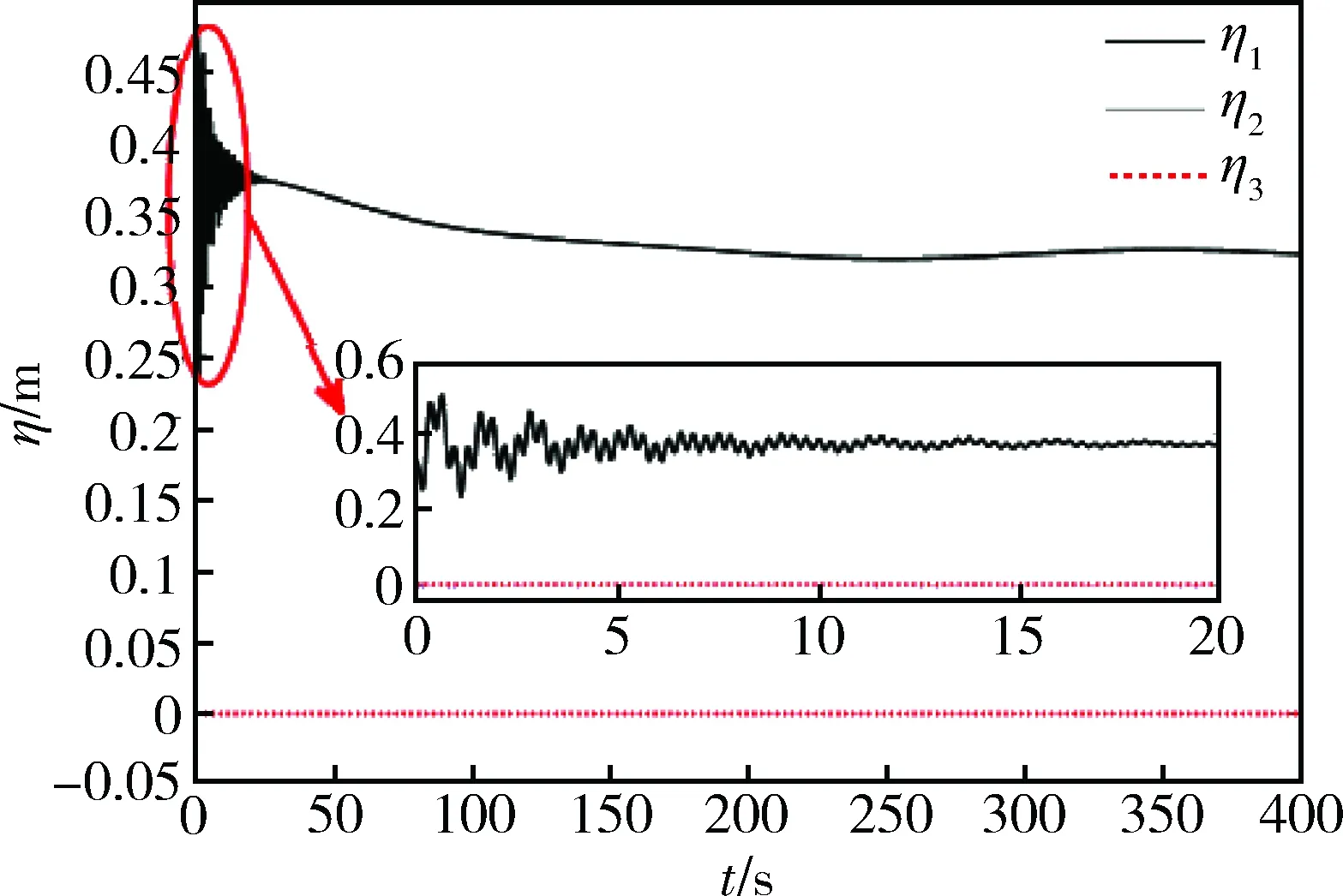
图6 弹性状态量变化曲线

由图1和2可知，实现了对参考飞行高度和速度的快速跟踪，并且稳态跟踪误差限定在零值附近。图3表明航迹角、攻角和俯仰角速度稳定地跟踪了指令信号。图4和5表明控制量输入平稳且在可实现的范围之内。图6表明在状态转移过程中，弹性模态的变化在系统允许的范围内。仿真结果说明设计的控制器达到了预定的控制目的。

5 结论

针对高超声速飞行器模型非线性、不确定性的特征，在反演设计的基础上，设计了一种动态面滑模控制器。引入一阶滤波器，避免了传统反演控制的“微分项膨胀”问题，利用双曲正切函数的平滑特性增强控制过程的稳定度，在控制器中设计滑模面的积分项消除静差。针对干扰上界的不确定设计自适应估计律，并引入自适应估计修正项，抑制自适应调节过程中的参数漂移，增强了控制器的鲁棒性。仿真结果表明，控制器很好地实现了对控制指令的跟踪且响应速度较快。

[1]FidanB,MirmiraniM,IoannouPA.FlightDynamicsandControlofAir-BreathingHypersonicVehicles：ReviewandNewDirections[C].AIAA-2003-7081, 2003.

[2] 时建明, 王洁, 王琨, 邵雷. 吸气式高超声速飞行器纵向运动反演控制器设计[J]. 西安交通大学学报, 2013, 47(3):102-107. (ShiJianming,WangJie,WangKun,ShaoLei.DesignofBacksteppigControllerforLongitudinalMotionofanAir-BreathingHypersonicVehicle[J].JournalofXi’anJiaotongUniversity, 2013, 47(3): 102-107.)

[3] 黄喜元,王青,董朝阳. 基于Backstepping的高超声速飞行器鲁棒自适应控制[J]. 系统工程与电子技术, 2011, 33(6): 1321-1326. (HuangXiyuan,WangQing,DongChaoyang.RobustAdaptiveControlofHypersonicVehiclesviaBacksteppingMethod[J].SystemsEngineeringandElectronics, 2011, 33(6): 1321-1326.)

[4]BialyBJ，KlotzJ,etal.AnAdaptiveBacksteppingControllerforaHypersonicAir-BreathingMissile[C].AIAA-2012-4468, 2012.

[5] 卜祥伟，吴晓燕，陈永兴，白瑞阳. 基于非线性干扰观测器的高超声速飞行器滑模反演控制[J]. 控制理论与应用, 2014, 31(11): 1473-1479. (BuXiangwei,WuXiaoyan,ChenYongxin,BaiRuiyang.Nonlinear-

disturbance-observer-basedSlidingModeBacksteppingControlofHypersonicVehicles[J].ControlTheory&Applications, 2014, 31(11): 1473-1479.)

[6] 于靖，陈谋，姜长生. 基于干扰观测器的非线性不确定系统自适应滑模控制[J]. 控制理论与应用，2014, 31(8): 993-999. (YuJing,ChenMou,JiangChangsheng.AdaptiveSlidingModeControlforNonlinearUncertainSystemsBasedonDisturbanceObserver[J].ControlTheory&Applications, 2014, 31(8): 993-999.)

[7] 梁勇，尚安利，邓方林. 一类非线性系统的动态面二阶滑模控制[J]. 系统工程与电子技术，2004,26(10):1468-1471. (LiangYong,ShangAnli,DengFanglin.DynamicSurfaceSecond-orderSlidingModeControlforaClassofNonlinearSystems[J].SystemsEngineeringandElectronics, 2004, 26(10): 1468-1471.)

[8] 王鹏，刘鲁华，吴杰. 高超声速飞行器Terminal滑模控制系统设计[J]. 航天控制，2012，30(5)：9-14. (WangPeng,LiuLuhua,WuJie.TheTerminalSlidingModeControlSystemDesignforHypersonicFlightVehicle[J].AerospaceControl, 2012, 30(5): 9-14.)

[9]HuXX,WuLG,HuCH,etal.AdaptiveSlidingModeTrackingControlforaFlexibleAir-breathingHypersonicVehicle[J].JournaloftheFranklinlnstitute, 2012, 349(2): 559-577.

[10]MichaelA.BolenderandDavidB.Doman.NonlinearLongitudinalDynamicalModelofanAir-BreathingHypersonicVehicle[J].JournalofSpacecraftandRockets, 2007, 44(2): 374-387.

[11]FiorentiniL.NonlinearAdaptiveControllerDesignforAir-breathingHypersonicVehicles[D].Columbus:TheOhioStateUniversity, 2010.

The Dynamic Surface and Sliding Mode Controller Design for Hypersonic Vehicles

Tan Shili, Wang Jie, Wang Pengfei

Air Force Engineering University, Xi′an 710051, China

Adynamicsurfaceandslidingmodecontrollerisdesignedforthelongitudinaltrackofflexiblehypersonicvehicles.Thelow-passfirstorderfilterisintroducedtoobtainthederivativesofvirtualcontrollaws,whichavoidsdifferentiationteen’sexplosionintheoriginalback-steppingcontrol.Thehyperbolictangentfunctionisintroducedinsteadofsignfunctionforchatteringeliminationintheslidingmodecontrol.Adaptivedisturbanceobserverisintroducedtoestimateandcompensatethemodeuncertaintiestoincreasethecontroller′srobust.Theresultofreferencetrajectorytrackingsimulationshowstheeffectivenessofthiscontrollerbytrackingvelocityandaltitudecommands.

Hypersonicvehicles;Slidingmodecontrol;Dynamicsurface;Back-stepping；Filter

2015-07-29

谭诗利(1991-)，男，湖北利川人，博士研究生，主要研究方向为高超声速飞行器控制理论与方法；王 洁(1967-)，女，陕西渭南人，博士，教授，主要研究方向为非线性控制理论；王鹏飞(1988-)，男，河南开封人，博士研究生，主要研究方向为高超声速飞行器受限弹性控制。

TP273

A

1006-3242(2016)04-0023-06