基于主动学习GA-SVM分类器的连铸漏钢预报
方一鸣 胡春洋 刘 乐 张兴明
1.燕山大学工业计算机控制工程河北省重点实验室, 秦皇岛,0660042.国家冷轧板带装备及工艺工程技术研究中心, 秦皇岛,0660043. 清华大学天津高端装备研究院,天津,300300
基于主动学习GA-SVM分类器的连铸漏钢预报
方一鸣1,2胡春洋1刘乐1张兴明3
1.燕山大学工业计算机控制工程河北省重点实验室, 秦皇岛,0660042.国家冷轧板带装备及工艺工程技术研究中心, 秦皇岛,0660043. 清华大学天津高端装备研究院,天津,300300
摘要:针对在小样本数据情况下训练的连铸漏钢预报模型难以获得较高预报准确率的问题,提出了一种基于主动学习遗传算法-支持向量机(GA-SVM)分类器的漏钢预报算法。该算法首先将采集到的连铸结晶器坯壳温度数据进行预处理,并将有效数据进行标注;然后利用标注后的小样本数据和遗传算法来优化SVM的经验参数,训练并得到支持向量机模型;最后利用某钢厂采集到的连铸结晶器坯壳温度数据进行测试。测试结果表明,在利用小样本数据进行训练的情况下,所提出的基于主动学习GA-SVM分类器的连铸漏钢预报算法具有较高的漏钢预报率(预报精度)和100%的漏钢报出率,验证了所提漏钢预报算法的有效性。
关键词:漏钢预报;GA-SVM;主动学习;小样本数据
0引言
漏钢是连续铸钢生产过程中最严重的事故之一。为防止漏钢事故的发生,国内外学者进行了大量漏钢预报算法的研究[1-2],其中以神经网络及其优化算法居多。厉英等[3]提出了采用变步长并加入动量项、防振荡项等方法加快神经网络收敛速度的BP神经网络漏钢预报模型。张本国等[4]提出了基于LM算法的BP神经网络的连铸漏钢预报算法。这些漏钢预报模型算法的共同特点是在模型使用初期,需要大量的漏钢数据对模型进行训练,然而漏钢在实际生产中是必须要尽力避免的,所以很难获取大量的漏钢数据,不利于模型的学习。
支持向量机(supportvectormachine,SVM)是建立在统计学习理论和结构风险最小化的基础上的[5]。与神经网络方法相比,该算法可最终转化成一个二次型寻优问题,理论上得到的是全局最优点,且不存在局部极小值问题,被认为是针对小样本统计预测学习的最佳理论[6-7]。但目前对SVM算法参数的选择尚缺乏成熟的理论依据,不同的参数选择可能会对算法的实际识别性能和效果产生显著影响。
基于上述分析,本文以支持向量机为分类器,首先推导出分类器的数学模型,利用遗传算法对其参数进行优化[8];然后借助主动学习[9-10]的思想,利用置信度函数对温度数据进行筛选标注;最后利用分类器的数学模型对标注后的黏结数据进行识别,使漏钢预报模型在小样本数据情况下也能获得较高的预报准确率。
1SVM算法基本原理
SVM方法是基于线性可分情况下的最优分类超平面提出的,要求能将两种类别无错误地分开,并且使分类间隔最大(图1)。前者能保证经验风险最小,后者能保证实际风险最小。
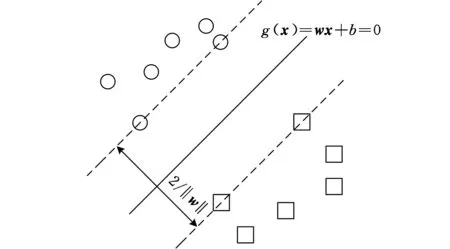
图1 最优分类超平面示意图
d维空间中线性判别函数的一般形式为g(x)=wx+b,其中,x∈Rd;w∈R1×d,为可调的权值向量;b为偏置,决定相对原点的位置。
设训练样本输入为x=xi,i=1,2,…,m,对应的期望输出为y=yi∈{1,-1},其中1和-1代表两种分类的类别标识。假定分类面方程为g(x)=wx+b=0,将判别函数归一化,如下所示:
(1)
这样就使得两个分类的所有样本都满足|g(xi)|≥1,即使得离分离面最近的样本的|g(xi)|=1,则对所有样本有下式成立:
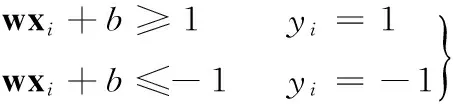
(2)
由式(1)可以计算出分类间隔为
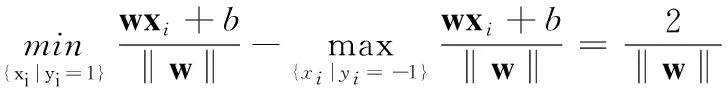
(3)
在约束式(1)的条件下最大化分类间隔2/‖w‖,等价于使‖w‖/2最小,那么求解最优超平面的问题就可以表示成如下的约束问题:

(4)
即在条件式(1)的约束下,求函数的最小值。
真实数据中噪声是不可避免的,很多数据是线性不可分的。此时允许某些样本点被误分,通过引入非负的松弛变量ξi来放松约束条件,如下所示:
yi(wxi+b)≥1-ξi
(5)
只有被错误分类的点对应的ξi是非零的。为了解这个不等式约束下二次型函数式(3)的极值问题,根据Karush-Kuhn-Tucker条件[11],可构造如下的Lagrange函数:
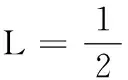
(6)
式中,m为训练样本数;αi>0,为Lagrange系数;C>0,为用户自定义的惩罚因子,用来调节对于输入样本被误分带来的影响。
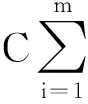
分别对w、b、ξ求偏微分,并令其等于0,得到如下结果:
(7)
(8)
(9)
将式(7)~式(9)代入式(6)中得
(10)
进一步可将上述L的极值问题转化为
(11)

(12)
又由Karush-Kuhn-Tucker条件,这个优化问题的解需满足:
αi[yi(wxi+b)-1+ξi]=0
(13)
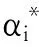
设求得的支持向量的个数为s,将式(12)代入式(2)中可以得到如下形式的分类函数:
(14)
其中,x为待分类样本。b*为分类阈值,可以由任意一对支持向量取中值求得,即
(15)
通过决策函数可以将不同类型的输入数据加以识别,从而输出不同的结果,达到分类的目的。
对于漏钢预报系统,大多数输入样本在输入空间是线性不可分的,这时可以通过非线性映射φ(x)将输入样本映射到高维特征空间构造分类面,则输入向量线性不可分问题在高维特征空间可以转化为线性可分问题来解决。映射之后得
(16)
引入核函数K(x,x′),只要该核函数满足Mercer定理[12],即K(x,x′)=φ(xi)φ(xj),则可避免φ(x)的直接运算。
由于径向基函数(RBF)对各种数据类型都具有良好的分类效果[13],所以本文采用RBF核函数,其函数的表达式为
(17)
式中,g为核函数系数。
选用RBF核函数后,求L极值问题可进一步表示为
(18)
同时分类函数变为
(19)
2基于主动学习GA-SVM的连铸漏钢预报模型的实现
2.1连铸结晶器坯壳外温度数据归一化
漏钢预报的实质就是一种动态波形的识别问题,即从热电偶检测到的温度波形中识别出符合漏钢特征的温度波形,原理示意如图2所示。
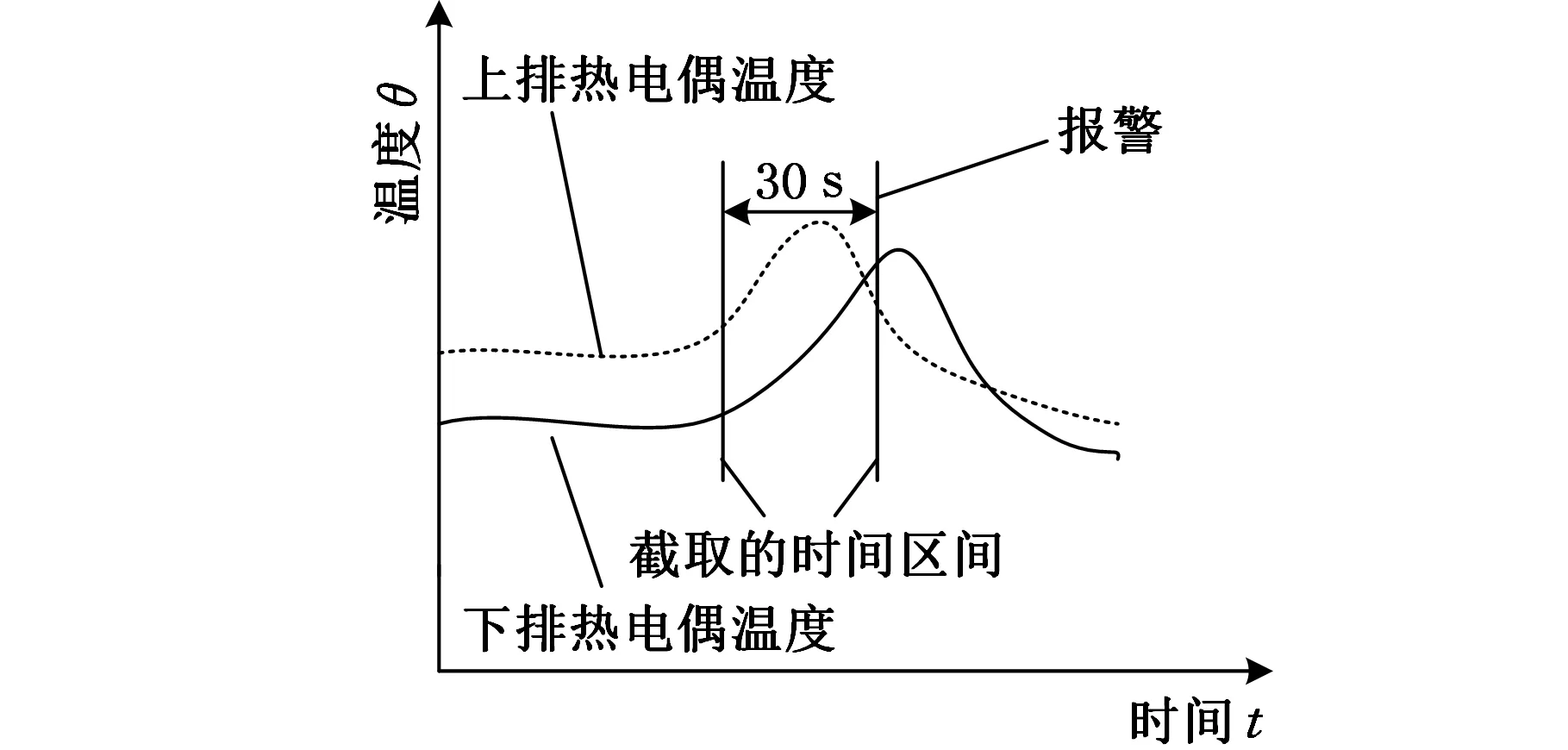
图2 漏钢预报原理示意图
在正常浇注过程中,铸坯坯壳凝固层的厚度自上而下递增,上排热电偶温度高于下排热电偶温度,热电偶所测温度波动也很小;当铸坯与结晶器发生黏结时,随结晶器的振动,黏结部位的坯壳很容易被拉裂,此时上排热电偶的温度会急剧升高;随黏结裂口的继续下移,上排热电偶温度因坯壳的固化弥合而逐渐下降;同理,当裂口到达下排热电偶位置时,也会发生温度先升后降的变化情况。
根据热电偶温度曲线的变化模式,截取图2所示区间内的温度采样值,进行归一化后作为SVM分类器的输入。根据某钢厂提供的漏钢温度数据,分析发现,单个热电偶的温度波动周期为30 s,热电偶温度的采样周期为1 s,故15个热电偶温度值即可体现一次漏钢特征的温度波形,选取相邻的15个温度值作为一个输入向量xi,xi∈R15×1;下一组相邻的15个温度值作为另一个输入向量xi+1。
为使原始数据处于同一区间内,在平等条件下进行分析,需对有效数据进行归一化处理,处理方式如下:
(20)
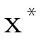
2.2引入遗传算法优化SVM模型
在式(18)中,最终的目标函数和约束条件中训练样本为已知数据,只有惩罚因子C和核函数参数g需要选择,并且两者对SVM分类器的性能有显著影响,因此需要对C和g进行优化。
遗传算法具有隐含的并行性和强大的全局搜索能力,可以在较短的时间内搜索到全局最优点。所以本文采用遗传算法来优化这两个参数。
首先对参数C和g进行二进制编码,构成图3所示的染色体。图3中,Clen、glen分别为对参数C、g进行二进制编码后的二进制数的位数长度。

图3 参数C和g的二进制编码图
参数C的变化范围取为[0.1,100],参数g的变化范围取为[0.01,1000],两者的编码公式为
(21)
式中,bin2dec()为将二进制数转化为十进制数的函数。
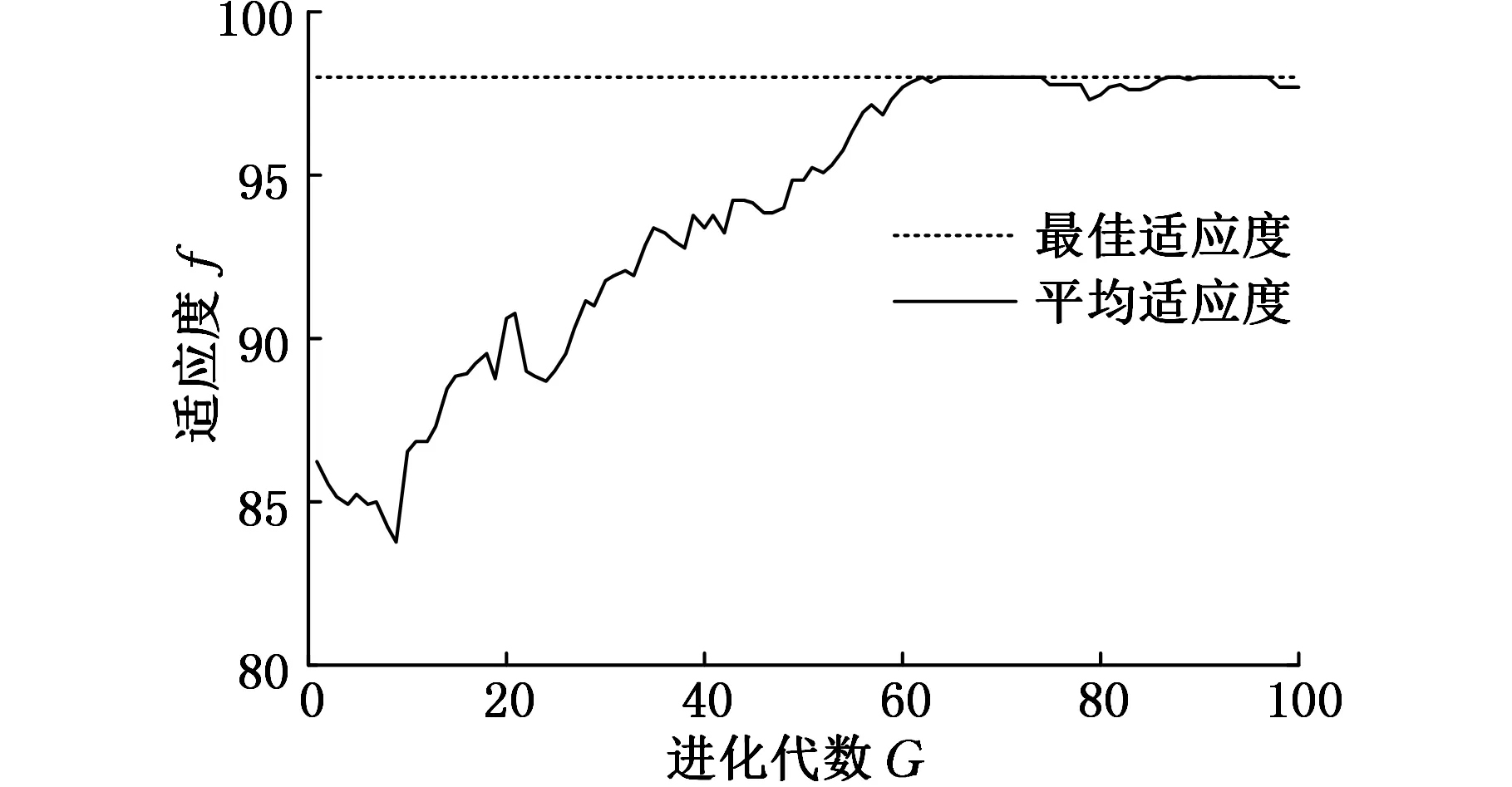
选取十折交叉验证的平均预测准确度作为适应度函数。
2.3主动学习GA-SVM模型的训练
为了提高连铸漏钢预报模型的预报准确度,本文基于主动学习的思想,将预处理后得到的温度数据,采用置信度评估方法进行选择标注后,加入训练集学习,这样训练出的模型能获得较高的分类准确度,同时减少了训练的样本数量,提高了训练效率。
对于两个类的分类问题,样本离分类超平面的距离反映了模型预测的置信度,定义置信度函数为
(22)
置信度函数的输出反映了样本点到分类器的距离,所以可以直接利用置信度函数值来确定训练样本的集合。离分类面越近的样本被误分的可能性越大,故只需选取置信度函数值的绝对值比较小的这些有“价值”样本作为训练集即可。
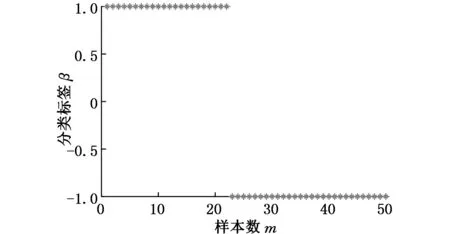
在[-1,1]区间内,取一适中的阈值δ(δ>0)。当h(x)>δ时,则输出分类函数f(x)=1,表示正常模式;同理当h(x)≤-δ,则输出分类函数f(x)=-1,表示漏钢模式;当-δ 主动学习GA-SVM分类器的具体训练步骤如下: (1)将漏钢数据进行归一化,利用主动学习方法对数据进行选择标注,作为训练样本和测试预报样本。 (2)对参数C和g进行二进制编码,并初始化种群。 (3)对种群的染色体进行解码获得C和g的值。将标注好的训练样本分为10等份,其中9组样本代入式(18)所示的SVM分类器模型,求出每个训练样本对应的αi,其中非零的αi对应的训练样本为支持向量,并将所得支持向量代入式(19)所示的分类函数对第10组进行预测。将预测结果与所标标签进行对比,取对比结果的准确率作为适应度值。然后,选取另外9组中任意一组作为预测数据,其余9组作为训练数据,重复上述过程,计算出每次的适应度值,取10次适应度值的平均值作为该10组染色体的平均适应度值。 (4)对染色体进行选择、交叉和变异操作,产生新一代种群。 (5)对新一代种群重复步骤(3)的操作,将遗传代数作为程序的终止准则,如果满足停止准则,则转到步骤(6),否则,返回步骤(4)。 (6)训练结束,得到最优参数C和g及对应的支持向量。 将训练得到的最优参数C和g代入式(19)的分类函数中,用于对测试样本数据进行预报测试。每当采集到一段时间内的现场漏钢温度数据后,可以根据式(22)筛选出一部分置信度值低的样本数据对漏钢预报模型进行更新训练,提高模型的泛化能力。 分类函数的预报测试过程如图4所示。 图4 用于漏钢预报的支持向量机模型 支持向量机模型形式上类似一个神经网络,其输出是若干中间层节点的线性组合,而每一个中间层节点对应于输入样本与一个支持向量的内积。 3预报模型的测试 利用某钢厂现场采集的历史数据,选出50组标注好的典型温度模式数据作为GA-SVM模型和BP神经网络模型的训练样本。其中,前22组为稳定模式样本,后28组为黏结漏钢模式样本(利用置信度函数筛选标注);选取195组已标注样本作为测试样本,前85组为黏结漏钢模式样本,中间100组为稳定模式样本,最后10组为伪漏钢模式样本。 GA-SVM模型训练过程中的一些参数初始值如表1所示。 选取十折交叉验证的平均准确率作为适应度。种群的进化趋势如图5所示。 表1 训练过程中的参数初始值 图5 GA-SVM模型种群适应度进化曲线(种群数量为50,终止代数100) 由图5可知,GA-SVM模型经过100代的训练后,平均适应度值达到了97.64,非常接近98的最佳适应度了。最优参数C和g分别为79.86和994.54。 网络模型的测试性能指标预报率ηp和报出率ηr的计算式为 (23) (24) 式中,nr为正确报警次数;nf为错误报警次数;no为漏报次数。 GA-SVM方法的训练结果如图6所示,从图6中可以看出:训练样本的分类准确率达到了100%。BP神经网络方法的训练结果如图7所示,训练样本的分类准确率也达到了100%。 利用训练好的GA-SVM模型与BP神经网络模型进行已标注样本的预报测试,GA-SVM模型的测试仿真结果如图8所示,BP神经网络模型的测试仿真结果如图9所示。 由图8可知,GA-SVM测试样本的预报结果为:报警次数87次,包括对全部报警样本的85次正确报警以及2次误报。 由图9可知,BP神经网络测试样本的预报结果为:报警次数88次,包括对全部报警样本中的83次正确报警以及5次误报、2次漏报。 图6 GA-SVM模型训练结果图 图7 BP神经网络模型训练结果图 图8 GA-SVM模型预报结果图 图9 BP神经网络模型预报结果图 将GA-SVM漏钢预报方法与BP神经网络漏钢预报方法相比较,结果如表2所示。 表2 BP神经网络与基于主动学习GA-SVM 由仿真结果和计算结果可以看出,在相同数量的训练样本进行模型训练的情况下,GA-SVM连铸漏钢预报模型具有更好的预报效果,得到了97.7%的漏钢预报率和100%的漏钢报出率,提高了漏钢预报系统对黏结漏钢温度模式的识别精度,降低了误报率。 4结论 本文提出的基于主动学习GA-SVM分类器的漏钢预报模型,利用支持向量机算法良好的泛化能力,克服了传统漏钢预报模型需大量漏钢数据进行训练的不足;结合遗传算法的全局寻优能力,克服了SVM算法参数选择缺乏理论依据的不足;采用基于主动学习思想的置信度评估方法对漏钢温度数据进行选择标注,提高了模型的训练效率及预报准确率。将该模型应用于连铸过程的漏钢预报,得到了97.7%的漏钢预报率及100%的漏钢报出率,提高了连铸漏钢预报模型的预报率和报出率,降低了漏钢误报率。 参考文献: [1]秦旭, 朱超浦, 尹延荣, 等. 液压伺服振动式板坯连铸机的漏钢预报技术[J]. 钢铁, 2010, 45(11): 97-100. QinXu,ZhuChaopu,YinYanrong,etal.ForecastingofMoltenSteelBreakoutsfortheSlabContinuousCasterswithHydraulicServoOscillationSystems[J].IronandSteel, 2010, 45(11): 97-100. [2]MillsKC,BillanyTJH.CausesofStickerBreakoutduringContinuousCasting[J].IronMakingandSteelmaking, 1991, 18(4): 253-265 [3]厉英, 王正, 敖志广, 等.BP神经网络漏钢预报系统优化[J]. 控制与决策, 2010, 25(3): 453-456. LiYing,WangZheng,AoZhiguang.OptimizationforBreakoutPredictionSystemofBPNeuralNetwork[J].ControlanDecision, 2010, 25(3): 453-456. [4]张本国, 李强, 王葛, 等. 基于改进BP神经网络的连铸漏钢预报[J]. 中国机械工程, 2012, 23(2): 204-207. ZhangBenguo,LiQiang,WangGe,etal.BreakoutPredictionBasedonImprovedBPNeuralNetworkinContinuousCastingProcess[J].ChinaMechanicalEngineering, 2012, 23(2): 204-207. [5]高隽. 人工神经网络原理及仿真实例[M]. 北京:机械工业出版社, 2007. [6]VapnikVN.StatisticalLearningTheory[M].NewYork:J.Wiley, 1998. [7]张新峰, 赵彦. 基于最小二乘支持向量机的小样本威布尔可靠性分析[J]. 中国机械工程, 2012, 23(16): 1967-1971. ZhangXinfeng,ZhaoYan.WeibullReliabilityAnalysisinSmallSamplesBasedonLSSVM[J].ChinaMechanicalEngineering, 2012, 23(16): 1967-1971. [8]陈果. 基于遗传算法的支持向量机分类器模型参数优化[J]. 机器科学与技术, 2007, 26(3): 347-350. ChenGuo.OptimizingtheParametrsofSupportVectorMachine’sClassifierModelBasedonGeneticAlgorithm[J].MechanicalScienceandTechnology, 2007, 26(3): 347-350. [9]ChengJian,WangKongqiao.ActiveLearningforImageRetrievalwithCo-SVM[J].PatternRecognition, 2006, 40(1): 330-334. [10]徐海龙, 王晓丹, 廖勇, 等. 一种基于主动学习的SVM增量训练算法[J]. 控制与决策, 2010, 25(2): 282-286. XuHailong,WangXiaodan,LiaoYong,etal.IncrementalTrainingAlgorithmofSVMBasedonActiveLearning[J].ControlandDecision, 2010, 25(2): 282-286. [11]曹建, 孙世宇, 段修生, 等. 基于KKT条件的SVM增量学习算法[J]. 火力与指挥控制, 2014, 39(7): 139-143. CaoJian,SunShiyu,DuanXiusheng,etal.SVMIncrementalLearningAlgorithmBasedonKKTConditions[J].FireControl&CommandControl, 2014, 39(7): 139-143. [12]NelloC,HohnS.AnIntroductiontoSuppotVectorMachinesandOtherKernal-basedLearingMethods[M].Cambridge:CambridgeUniversityPress, 2000. [13]MartensD,BaesensB,vanGestelT.DecompositionalRuleExtractionfromSupportVectorMachinesbyActiveLearning[J].IEEETransactiononKnowledgeandDataEngineering, 2009, 21(2):178-191. (编辑袁兴玲) 收稿日期:2015-07-28 基金项目:国家自然科学基金委员会与宝钢集团有限公司联合资助项目(U1260203);国家自然科学基金资助项目(61403332);河北省自然科学基金-钢铁联合基金资助项目(F201320329);河北省高等学校创新团队领军人才培育计划资助项目(LJRC013) 中图分类号:TF345 DOI:10.3969/j.issn.1004-132X.2016.12.009 作者简介:方一鸣,男,1965年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为冶金自动化系统(轧机自动化、连铸结晶器振动控制),系统集成和计算机控制,复杂系统建模仿真和控制,自适应、鲁棒控制理论与应用。胡春洋,男,1988年生。燕山大学电气工程学院硕士研究生。刘乐,男,1985年生。燕山大学电气工程学院讲师。张兴明,男,1989年生。清华大学天津高端装备研究院研发工程师。 BreakoutPredictionClassifierforContinuousCastingBasedonActiveLearningGA-SVM FangYiming1,2HuChunyang1LiuLe1ZhangXingming3 1.KeyLabofIndustrialComputerControlEngineeringofHebeiProvince,YanshanUniversity,Qinhuangdao,Hebei,066004 2.NationalEngineeringResearchCenterforEquipmentandTechnologyofColdStripRolling,Qinhuangdao,Hebei,066004 3.TianjinResearchInstituteforAdvancedEquipment,TsinghuaUniversity,Tianjin,300300 Abstract:Aiming at the problem that was difficult to obtain a high accurate breakout prediction model of continuous casting in the case of small sample data, a breakout prediction algorithm was proposed based on active learning GA-SVM classifier. Firstly, the algorithm preprocessed temperature data of continuous casting mold and labels valid data. Secondly, SVM model was obtained after SVM empirical parameters were optimized using labeled small sample data and GA. Finally, the optimized SVM model was tested using the historical data of a steel plant. The results show that in the case of small sample data for training model, the breakout prediction algorithm based on active learning GA-SVM classifier can obtain higher breakout prediction accuracy and 100% reported ratio. The presented breakout steel prediction algorithm was validated. Key words:breakout prediction; genetic algorithm-support vector machine(GA-SVM); active learning; small sample data