考虑容量约束的电缆敷设变邻域搜索优化算法

梁　涛　李卫东　徐爱东

1(山东电力工程咨询院有限公司　山东 济南 250013)2(华能西宁热电有限责任公司　青海 西宁 810000)



考虑容量约束的电缆敷设变邻域搜索优化算法

梁涛1李卫东2徐爱东1

1(山东电力工程咨询院有限公司山东 济南 250013)2(华能西宁热电有限责任公司青海 西宁 810000)

摘要针对一类考虑容量约束的电缆敷设优化问题，提出一种新的变邻域搜索优化算法。首先，分析电缆敷设问题的优化要求，基于图论给出具有容量约束的电缆敷设优化问题的数学描述；然后，结合问题特征提出基于Dijkstra算法的初始解生成策略，构建依据解间距离的邻域结构和局部启发式搜索策略，在此基础上给出电缆敷设变邻域搜索优化算法；最后通过实例求解结果表明，该算法能在短时间内获得问题的最优解或近优解，验证了算法的有效性和优越性。

关键词电缆敷设变邻域搜索优化算法

0引言

电缆敷设是发电厂工程建设中一项复杂且重要的工作内容。合理的敷设优化不但能减少电缆和周围环境相互干扰而引起的事故概率，而且能够显著节约电缆及桥架使用量。同时电缆长度的减少可明显降低电缆施工的工程量，无疑为电厂的投资带来可观的经济效益。另一方面，电缆的敷设优化又受到工艺系统布置、桥架容量和不同电压等级电缆电磁干扰等诸多因素影响，导致电缆敷设优化问题成为一类典型的NP-Hard问题。因而，引起了科学研究和工程设计领域的普遍关注[1,2]。

现阶段，在国内工程设计中应用的电缆敷设优化工具主要有从法国引进的PERICLES和国产的AUTOLAY软件等[3,4]。这些软件大多采用Dijkstra算法或Floyd算法。这两种算法作为经典的最短路径算法，对于无容量约束的最短路径问题具有较高的求解效率，但较难用于具有容量约束的路径优化问题。另外，文献[5]在其设计的电厂电缆敷设计算机辅助设计与管理系统(CADMCL)中提出了应用人工智能方法来解决电缆路径寻优问题；文献[6]针对电缆敷设设计问题，引入了一种树状或网状优化算法，用于提高设计水平，并将其应用于脱硫改造工程施工。这些方法本质上属于基于规则的启发式方法，求解过程简单快速，但对于大规模优化问题较难保证求解的优化性。目前，考虑容量约束的电缆敷设优化问题仍是工程设计优化研究中面临的一个难题。

变邻域搜索VNS(VariableNeighborhoodSearch)作为一种新兴的智能优化算法，从1997年被首次提出[7]，至今经过十多年的研究和扩展，已被成功应用于旅行商问题、图着色、车辆调度等问题中。在解决优化问题，尤其是大规模组合优化问题上体现出了良好性能[8-10]。但是，此算法的寻优能力很大程度上依赖于邻域构建的合理性和局部搜索策略的有效性。本文针对具有容量约束的电缆敷设问题特点，在分析邻域结构与局部搜索策略构建方法的基础上，提出一种新的电缆敷设变邻域搜索优化算法，并应用实例验证了该方法的有效性和优越性。

1问题描述

实际工程中的电缆敷设问题是将几千甚至几万根的动力电缆、控制电缆和信号电缆通过由桥架、电缆沟等组成的电缆通道从起点设备连接至终端设备。该问题的关键在于在电缆各通道都有其固定容量的前提下，数量如此庞大的电缆分别走哪条路径才能使整个系统更稳定、更经济。为更好地描述该问题，首先给出以下定义：

定义1设G=(V,E)为一个无向图，V为非空的顶点集，E为边集，若满足：

① 在G的边集E上定义非负实值函数d，称为长度函数，对任意e∈E，称d(e)为边e的长度。

② 在G的边集E上定义非负整值函数c，称为容量函数，对任意e∈E，称c(e)为边e的容量。

③S与F是两个长度为M的非空顶点序列；对任意s∈S，f∈F，均有s∈V，f∈V。

则称图G为一个敷设图，简记为L=(V,E,d,c,S,F)。其中，由序列S、F中顶点构成的顶点对(s1,f1),…,(sM,fM)表示待敷设的路径。在图G中从路径的起点s到终点f找出一条连通的途径，称为路径的敷设，且将其上敷设路径数达到其最大容量的边称之为满边。

若选择电缆敷设总长度最短作为优化目标，则考虑通道容量约束的电缆敷设问题就等价于在一个敷设图L中，求其所有待敷设路径敷设长度和的最小值。该优化问题也可表示为如下数学规划模型：

Minz=∑k∈K∑(i,j)∈Edijxijk

(1)

s.t.

∑(i,j)∈Exijk=∑(i,j)∈Exjikk∈K,i≠sk,i≠fk

(2)

∑(i,j)∈Exijk=1k∈K,i∈skorj=fk

(3)

∑(i,j)∈Exjik=0k∈K,i∈skorj=fk

(4)

∑(i,j)∈E(xijk+xjik)≤cijk∈K,i>j

(5)

xjik=0 or 1

(6)

其中，xijk为表示敷设路径k是否从顶点i到顶点j经过边(i,j)的决策变量，1表示是，0表示否；dij为边(i,j)的长度，K为待敷设路径集合，sk、fk分别代表敷设路径k的起点和终点，cij为边(i,j)的容量。若存在特殊类型电缆的专用路径，例如某桥架为动力电缆桥架，不允许控制和信号电缆通过，只需将约束条件式(7)增加到上述模型中，其中E1为动力电缆桥架对应的边集，K2、K3分别为控制和信号电缆对应的敷设路径集合。其他电缆专用路径同理。

xijk=0,(i,j)∈E1,k∈K2∪K3

(7)

电缆敷设优化的目标也可以是电缆投资最省，即电缆总费用最少，只需将优化目标式(1)中各类不同价格的电缆长度相加之前乘以其单位价格即可。

2变邻域搜索算法

变邻域搜索算法(VNS)的基本思想是从一个初始可行解出发，在搜索过程中通过多次系统地改变邻域结构集来拓展搜索范围，不断地从一个局部最优解移向另一个更优的局部最优解。应用VNS求解优化问题，首先需要给出一个初始可行解。另外，根据应用问题特征，构建合适的邻域结构和局部搜索策略是实现算法优越性能的关键。

2.1初始解的构造

在电缆敷设问题对应的敷设图L中，所有待敷设路径的一次成功敷设，就形成了该问题的一个解。若敷设后，对于任意e∈E，其上经过的路径数cr都满足cr≤c(e)，则该解即为电缆敷设问题的一个可行解。由此可见，初始可行解可以通过在合适的顺序下逐条进行路径的敷设来获得。为保证初始解的局部优化性，减少搜索时间，可以在考虑各边容量的基础上应用Dijkstra算法获得各路径的敷设，即每次应用Dijkstra算法时所用的边集E′为当前的可用边集，需从边集E中去除当前的满边以及与当前待敷设路径电缆类型不匹配通道的对应边。这样既保证了获得解的可行性，又兼顾了获得解在当前敷设顺序下的最优性。路径的敷设顺序可以采用赌轮法生成，若一次敷设无法获得可行解，则需要变更敷设顺序或重新生成新的敷设顺序。

2.2邻域结构的构建

首先针对电缆敷设问题特点，给出两个解之间距离的定义：

定义2设x1,x2为电缆敷设问题的两个可行解，若x1中所有路径的敷设存在k条路径与x2中不同，而其他M-k条路径的敷设相同，则称解x1,x2之间的距离为k，记为：

δ(x1,x2)=k

(8)

由以上定义，本文依据不同解之间距离的远近来定义解的邻域结构。换句话说，将与解x距离为k的解的集合定义为解x的邻域Nk，即：

Nk={x′|δ(x,x′)=k}k=1,2,…,M

(9)

对于考虑容量约束的电缆敷设问题，这样定义邻域结构的好处在于可以直观地进行邻域内搜索和搜索范围拓展。

进行邻域内搜索时，由解x获得邻域Nk内的另一个解x′，只需随机选择k条路径变换敷设即可。变换敷设时，先在敷设图L中将选中路径的敷设删除，将原路径其中一条边设置为不可用，然后应用Dijkstra算法在可用边范围内重新敷设该路径。如此既保证了获得的解x′∈Nk，又兼顾了解的优化性。

2.3局部搜索策略

局部搜索的目的是在可行解附近的局部区域内获得更优解。局部搜索策略的好坏很大程度上决定着局部搜索过程中解是否能够被改进。本文采用在解x′的邻域Nm2内进行启发式搜索的策略：

针对图中一条满边定义两个路径集合KA和KB，分别表示途经该边的路径集和不途经该边的路径集。通过随机互换KA中某条路径和KB中某条路径的敷设顺序来搜索更优解。

经过简单分析可知，考虑容量约束的电缆敷设问题无法应用Dijkstra算法直接求解是因为进行路径敷设时存在满边，而决定解是否优化的关键在于满边上敷设哪些路径。换言之，应用Dijkstra算法直接求解可能导致某边e上敷设的路径数cr超出其容量约束，产生不可行解。在考虑容量约束的条件下，此cr条路径中哪些路径能够途经边e很大程度上决定着对应解的可行性和优化性，而前者又取决于这些路径的敷设顺序。由此可见，通过互换可行解中两条路径的敷设顺序可以达到局部搜索寻优的目的。然而，若互换敷设顺序的两条路径均不途经满边或者均途经相同的满边，难以实现解的实质性改进。因此，通过上述启发式搜索策略，更容易发现由于路径敷设顺序随机导致的解的次优点，从而进行修正。局部搜索的次数可根据问题的规模确定，无经验的情况下，推荐选择区间[10,50]内的一个整数。

2.4电缆敷设变邻域搜索优化算法

基于2.1节-2.3节的分析，考虑通道容量约束的电缆敷设变邻域搜索优化算法描述如下：

Step1在考虑容量约束的基础上，应用Dijkstra算法逐条路径敷设，从而获得一个初始可行解x。

Step2定义x的邻域结构Nk={x′|δ(x,x′)=k}(k=1,2,…,M)。

Step3设置k=1。

Step6若获得的局部最优解x′优于当前最优解x，则更新当前最优解x=x′，转至Step3；否则，设置k=k+1。

Step7若k≤M，则转至Step4；否则，算法结束。

3实例求解与分析

为了验证电缆敷设变邻域搜索优化算法的有效性，本文对五个不同规模的实例进行了建模和求解。算法采用C++进行编程实现，在CPU为2.66GHz、内存为1GB的PC机上进行求解。实例1-实例5均为随机实例，其电缆通道的连接方式、各段长度与容量以及需要敷设的电缆集均为随机生成。由于实际三维空间中各通道交点上连接的通道一般不超过六个方向，为保持实例与实际问题的一致性，在保证敷设图中所有顶点间均存在连通途径的基础上，每个顶点上连接的边数均不大于六。

应用本文算法对实例1-实例5进行优化求解的结果如表1所示。作为比较，表1中同时给出了基于第1节中数学规划模型应用数学优化求解器LINDOAPI5.0对五个实例在同一配置PC机上进行优化求解的结果。从表1中可以看出，对于规模较小的实例1和实例2，两种方法均能找到问题的最优解，而本文方法的所用的求解时间比LINDO的求解时间要少得多。随着问题规模的增大，最优解越来越难被找到。对于较大规模的实例3-实例5，基于数学规划模型利用求解器LINDO在规定的时间内只能找到问题的近优解。甚至由于模型规模巨大出现内存不足错误，而本文方法则可以在更短的时间内获得更优的可行解。这主要归功于算法中邻域结构和局部启发式搜索策略构建的有效性，特别是局部启发式搜索策略。表2中给出了在同一初始解的情况下利用局部随机搜索策略和局部启发式搜索策略求解结果的比较，同时给出了对应无容量限制电缆敷设问题的最优解作为下限值提供参考。从表2中可以看出，相对于局部随机搜索策略，本文提出的局部启发式搜索策略对初始解的改进效果明显，获得的结果与参考下限之间的距离均小于2%。考虑到容量约束条件使最优解与参考下限之间可能的偏离距离，由此可见本文方法的优越性。

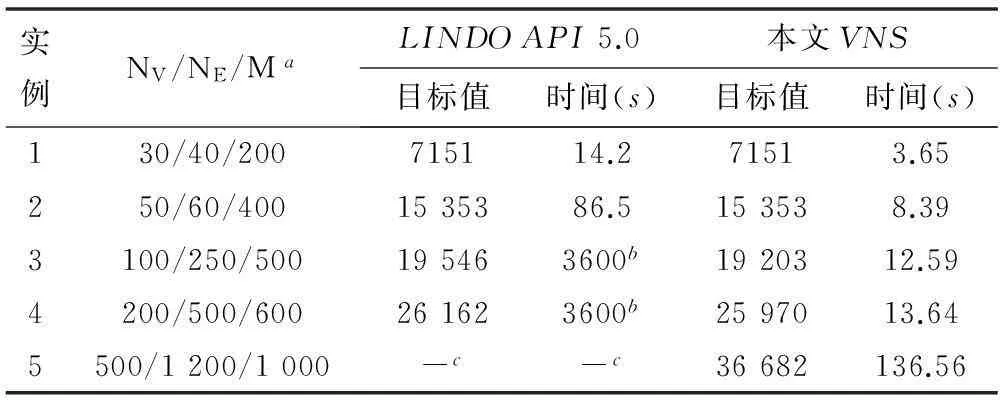
表1　实例求解结果比较表

注：aNv/NE/M表示实例的节点数/边数/电缆数；

b经过相应的时间结束计算，将最佳可行解作为优化结果；

c由于模型规模太大，无法完成计算过程

表2　局部搜索策略效果比较表

4结语

考虑容量约束的电缆敷设优化问题是目前工程设计优化领域面临的难题之一。本文针对具有通道容量约束的电缆敷设问题特点，提出了敷设图的概念，在此基础上给出了一种新的适合电缆敷设优化问题的变邻域搜索算法。该算法邻域结构构建简单、直观，局部启发式搜索策略合理、有效，较好地保证了搜索过程的快速趋优性。实例计算结果验证了该算法不但具有较快的求解速度，而且具有较好的寻优性能。特别是对于较大规模问题，该算法优势明显，在解决电缆敷设优化设计问题领域具有较好的应用前景和推广价值。

参考文献

[1] 王铖.火力发电厂电缆敷设路径优化研究[J].绍兴文理学院学报,2011,31(10):58-62.

[2] 王爱梅,张悦,郭晓玲.发电厂电缆敷设优化方式探讨[J].山西电力,2013,33(2):70-72.

[3] 陈智,游建伟.秦山核电二期工程核岛电缆敷设设计实践[J].核动力工程,2003,24(2):201-203.

[4] 安庆敏,徐爱东,陈志强,等.火力发电厂热控电缆敷设软件的开发与应用[J].工业仪表与自动化装置,2011,41(6):64-66.

[5] 王明海.电厂电缆敷设设计与工程管理系统的研究[D].华北电力大学,2004.

[6] 罗建国,韦思亮.基于树状、网状搜索算法的电缆敷设设计与应用[J].热力发电,2013,42(3):103-105.

[7]MladenovicN,HansenP.Variableneighborhoodsearch[J].Computers&OperationsResearch,1997,24(11):1097-1100.

[8]AvanthayC,HertzA,ZuffereyN.Avariableneighborhoodsearchforgraphcoloring[J].EuropeanJournalofOperationsResearch,2003,151(2):379-388.

[9] 张则强,谭思捷,黄玉真,等.求解单行布局问题的一种变邻域搜索算法[J].中国机械工程,2013,24(20):2791-2796.

[10] 陈萍,黄厚宽,董兴业.求解多车型车辆路径问题的变邻域搜索算法[J].系统仿真学报,2011,23(9):1945-1950.

A VARIABLE NEIGHBOURHOOD SEARCH ALGORITHM FOR CABLE LAYOUTPROBLEMSWITHCAPACITYCONSTRAINTS

Liang Tao1Li Weidong2Xu Aidong1

1(Shandong Electric Power Engineering Consulting Institute Co., Ltd., Jinan 250013,Shandong,China)2(Huaneng Xining Thermal Power Co., Ltd., Xining 810000,Qinghai,China)

AbstractWe presented a new optimised variable neighbourhood search algorithm for a kind of cable layout optimisation problem with capacity constraints. First, we analysed the optimisation demands of cable layout problems, and presented based on graph theory the mathematical description of cable layout optimisation problem with capacity constraints. Then in combination with the problem features, we introduced an initial solution generation strategy using Dijkstra algorithm, and built up a solution-distance-based neighbourhood structure and a local heuristic search strategy. On this basis, we proposed the optimised variable neighbourhood search algorithm for cable layout. Finally, it was demonstrated through the example of solving results that the presented algorithm could obtain optimal solutions or near-optimal solutions in a short time, which verified the effectiveness and superiority of the algorithm.

KeywordsCable layoutVariable neighbourhood searchOptimisation algorithm

收稿日期：2014-11-17。梁涛，工程师，主研领域：复杂系统建模与优化，电力系统运行与控制技术。李卫东，高工。徐爱东，教授级高工。

中图分类号TP391.9TM621

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.069