复杂网络中基于WCC的并行可扩展社团挖掘算法

亚森·艾则孜　李卫平　郭文强

1(新疆警察学院信息安全工程系　新疆 乌鲁木齐 830013)2(铁道警察学院公安技术系　河南 郑州 450053)3(新疆财经大学计算机科学与工程学院　新疆 乌鲁木齐 830013)



复杂网络中基于WCC的并行可扩展社团挖掘算法

亚森·艾则孜1李卫平2郭文强3

1(新疆警察学院信息安全工程系新疆 乌鲁木齐 830013)2(铁道警察学院公安技术系河南 郑州 450053)3(新疆财经大学计算机科学与工程学院新疆 乌鲁木齐 830013)

摘要WCC(Weighted Community Clustering)通过复杂网络中社团含有的三角数量来评价社团挖掘算法的性能。在原始的WCC算法中，需要在每次迭代中对所有的社团变化计算WCC值，因而计算量非常大。为了减小社团变化带来的WCC计算量，提出一种并行可扩展的社团挖掘算法。对应用WCC进行社团评价的方法进行分析，提出一种包含预处理、初始划分和划分改进三个阶段的并行社团挖掘算法。在划分改进中，由于每次社团变化都需要计算大量的WCC提升，基于社团的统计量提出一种WCC近似计算方法。大量的真实数据集实验表明，提出的社团挖掘算法与相关算法相比较，不仅社团检测的准确性更高，而且具有更好的并行可扩展性。

关键词复杂网络社团挖掘并行算法可扩展性

0引言

近些年，复杂网络分析已经成为数据挖掘领域的重要研究内容之一。复杂网络分析可广泛应用于社会学、生物学、信息科学等众多领域[1,2]。在对这些复杂网络进行分析的方法之中，社团挖掘是最重要的研究内容之一。在复杂网络中，社团又被称为聚类，是一组紧密相连的节点集合。社团内部节点的链接是紧密的，而不同社团节点之间的链接是松散的[3]。通过社团检测，研究人员可以深入地了解网络的结构信息[4]，网络中节点之间的交互关系[5]，以及节点在网络的进化中起到的作用[6]。

社团检测往往需要很大的计算量，各种社团挖掘算法很难扩展到含有数十亿边规模的复杂网络上。在2013年，Yang等[7]给出了真实网络的基准测试数据集，并包含了数据集中社团的正确划分。在该研究中，他们测试了不同最新社团挖掘算法[8-12]的执行时间，通过对比发现这些算法很难扩展到边规模为数千条的复杂网络。虽然BigClam[7]算法是针对大规模网络设计的，但是该算法仍然不能处理含有20亿条边的Friendster数据集。此外，虽然Louvain算法[8]可以处理和Friendster数据集具有相同规模的数据集，但是社团挖掘的质量却很低。

为了保持社团挖掘结果的准确性，同时提高应对海量数据的能力，本文提出一种两阶段的社团挖掘算法。在第一个阶段，采用聚类系数作为启发式方法获得网络的初始社团分割。在第二阶段，通过对不同社团中的节点进行移动对第一阶段得到的初始分割进行优化。在每次的社团调整过程中，通过增加社团的WCC[13]进行节点的移动。为了加速第二阶段的社团调整过程，本文提出一种新的WCC评估器。该WCC评估器类似于传统的WCC评价方法，但是却有着更高的计算效率。

1基于WCC的社团挖掘算法

对于给定的无向无权图G=(V,E)，本文的目标是通过最大化WCC值来挖掘图中的不相交社团。本节首先描述了社团挖掘的WCC指标，然后基于WCC指标提出了相应的社团挖掘算法，接下来分析如何应用提出的算法对WCC值进行估计，最后分析了算法的复杂性。

1.1WCC指标

WCC是一种复杂网络社团挖掘评价指标，该指标认为真实网络中的社团结构往往含有大量的三角。由于社团是由紧密相连的节点组成，那么这些节点构成三角的概率要相对较高，WCC应用该特征对图的节点集合划分(即社团划分)进行量化。

给定图G=(V,E)，节点x以及社团C，令t(x,C)表示x与C中节点构成的三角的个数，vt(x,C)表示C中能与x构成三角的节点的个数，那么将节点x与社团C的凝聚水平WCC(x,C)进行如下定义：

(1)

基于式(1)，社团C的WCC的计算公式为：

(2)

给定集合C，WCC(C)是C中所有节点的WCC的值的平均值。给定图分割P={C1,C2,…,Cn}，并且C1∩…∩Cn，那么P的WCC为该划分中所有社团的WCC的加权平均值，其计算公式如下：

(3)

1.2社团挖掘算法

为了对图G进行划分得到P，本文提出一种最大化WCC(P)社团挖掘算法。该算法包含数据的预处理、初始划分和划分改进三部分。

1.2.1预处理

在图G=(V,E)的加载时，进行如下的预处理操作：对于G中的每条边e∈E，计算e可以构成的不同三角的个数，并移除那些不能构成三角的边。

在预处理结束后，得到的图为G′。预处理操作存在如下两个优点：(1)WCC的计算并不依赖于这些边，因而可以提高计算效率；(2) 通过移除不能构成三角的边可以大幅压缩图的存储空间，从而节省内存开销。

1.2.2初始划分

该阶段对预处理得到的图G′进行初始划分，其基本思想是：节点的聚类系数越大，那么该节点与邻居节点形成的三角个数越多，因而该节点的邻居节点形成三角的概率也越大。依据式(1)，如果节点的聚类系数越大，那么与该节点同属于一个社团的那些邻居节点的WCC概率越大。

1.2.3划分改进

在得到初始划分后，需要对划分进行不断改进直到找到最优划分。在划分改进阶段，使用爬山搜索策略。在每次迭代中，通过一系列变换操作(3种)，依据原有的划分得到WCC值更高的划分。迭代终止的条件为迭代前后划分的WCC值变化小于阈值，或者迭代到一定的次数。

在每次迭代中，对于图中的所有节点v∈V，在下列三种变换操作中选取一个最佳变换，使得变化后得到的划分较变换之前是最优的：

• 不进行变换：使节点v处于原来的划分C中。

• 移除：将节点v从原来的划分C中移除并作为单体社团。用WCCR(v,C)来表示移除操作得到的WCC提升值，令P={C1,…,C,…,Ck}为原来的划分，P'={C1,…,C′,…,Ck,{v}}为变换后的划分，对于给定的图G=(V,E)，WCCR(v,C)的计算公式如下：

WCCR(v,C)=WCC(P′)-WCC(P)=-WCCI(v,C′)

(4)

其中C=C′∪{v}。

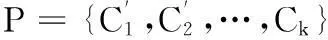
WCCT(v,C1,C2)=WCC(P′)-WCC(P)

(5)

在每次迭代中，由于每个节点之间的变换操作是相互独立的，所以可以并行地运行，因此可以大大提高算法的运行效率。

1.3WCCI值估计

WCC值的精确计算需要知道目标节点及其邻居节点构成的三角个数，对于含有d个邻居的节点，该操作的计算复杂度为O(d2)。由于网络节点度数的幂率分布特征，在并行计算模式下，极少数度数大的节点的计算时间往往影响着整个算法的运行效率。此外，在每次迭代过程中都需要计算WCC的提高值WCCI，因此WCCI的计算性能决定着算法的整体效率。为了加速WCCI的计算，本文提出了一种近似计算方法，该方法的基本思想如图1所示。

图1　WCCI的计算示意图

当节点v被加入到社团C时，WCC值的提高值为WCCI。对于节点v，仅仅考虑C中与v相连的节点的个数din。对于每个社团C，记录如下的统计量：节点个数r，边的密度δ，社团边界的边的个数b。同时，保存着图G的聚类系数ω(常数)。基于上述统计量，应用如下公式得到WCCI的估计值：

(6)

其中θ1、θ2和θ3分别为相应变量的系数，并且和为1。

2实验结果与分析

本节通过大量的真实数据集实验对算法的性能进行了评估。

2.1数据集与性能指标

本文的实验采用Stanford提供的公开网络数据集SNAP(http://snap.stanford.edu)，其中包括Amazon、Dblp、Youtube、LiveJournal、Orkut和Friendster六个网络数据集。这些数据集的基本统计信息如表1所示。

表1　数据集基本信息

2.2实验结果

在实验中，我们将本文提出的可扩展的社团检测算法记为scd，并将该算法与walktrap[8]、louvain[9]、oslom[10]、infoman[11]和bigclam[12]五种社团挖掘算法进行了对比。

首先，应用六种社团挖掘算法对上述的6个网络数据集进行社团检测，并对比了社团挖掘结果的准确性。图2和图3分别为六种算法在不同数据集上的F1值和NMI对比图。在这两个柱状图中，如果数据集对应的柱为空，说明相应算法的F1值或NMI值几乎为0。从这两幅图中可以看出，除了walktrap和louvain两种算法在Amazon数据集上的NMI值大于scd算法外，scd算法在其他数据集上的NMI和F1值都高于其他算法。这说明本文提出的社团挖掘算法对于不同类型的网络都具有更好的社团检测性能。

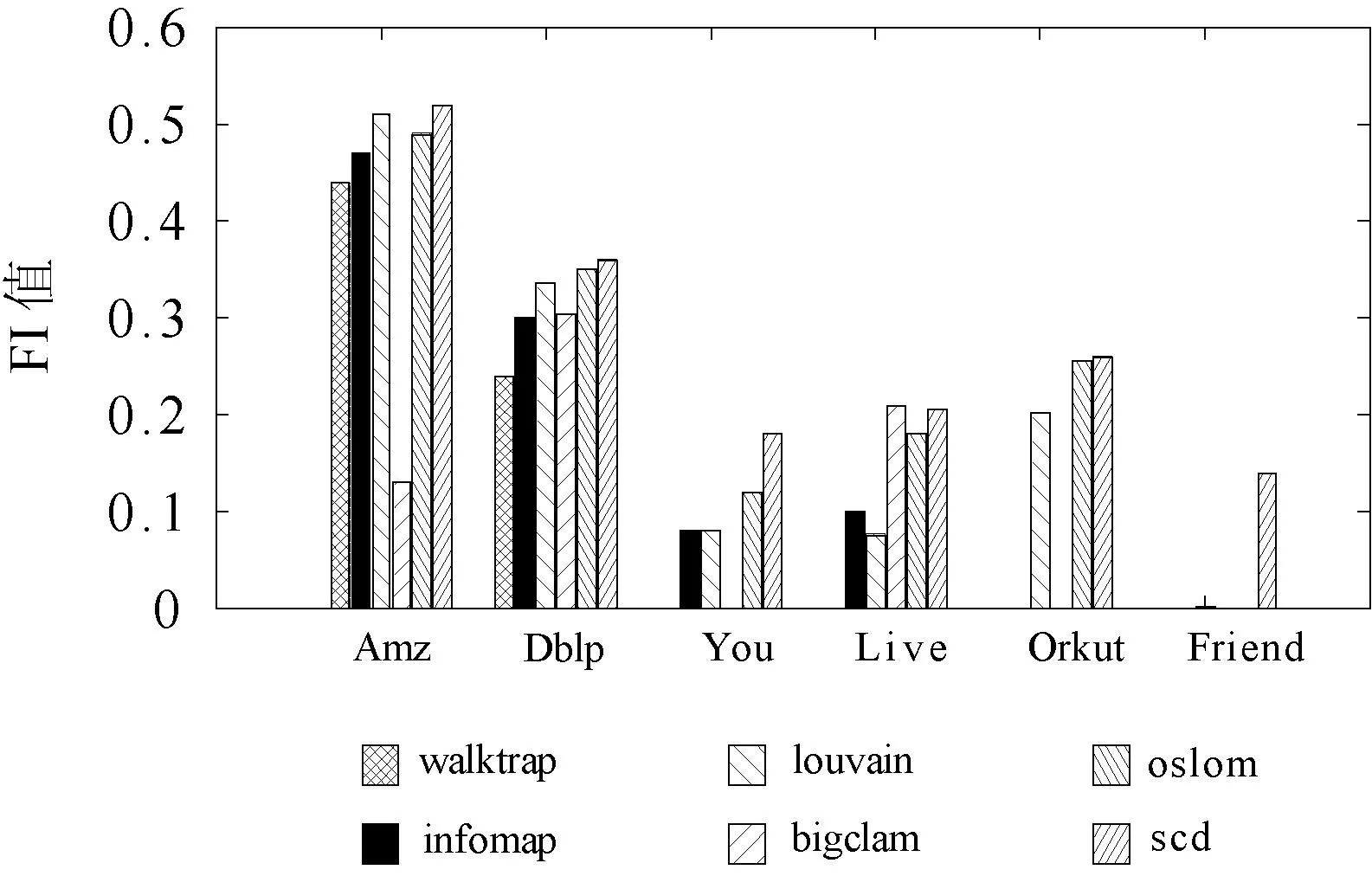
图2　算法的F1值对比

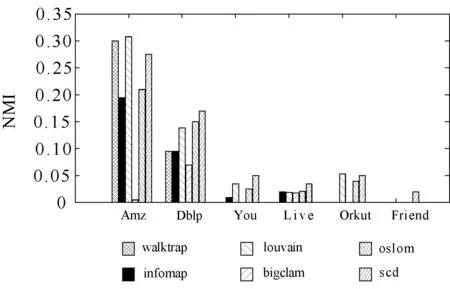
图3　算法的NMI对比

其次，通过实验对比了六种算法在这些数据集上的执行效率，实验结果如图4所示。在该组实验中，我们省略了那些准确性几乎为0的算法，令相应的柱值为空。从该图可以看出本文提出的算法的执行时间在6个数据集上的执行时间都是最短的，而louvain算法次之。我们对算法进行并行化，分析了scd算法在不同数量线程下的运行效率。在图5中，横轴表示算法的线程数量，纵轴为算法的运行时间，由于算法在单线程下的运行时间大于1秒，为了更好地对实验结果进行展示并在1秒处进行了截断。从图5可以看出，由于对scd算法进行了并行化，因此算法的执行时间明显减少了，并且在LiveJournal、Orkut和Friendster三个数据集上的并行效果要优于其他三个数据集。

图4　算法的执行效率对比

图5　scd算法的执行时间评估

最后，我们进一步分析了scd算法的并行化性能。图6为scd算法在不同算法下的运行时间，横轴表示网络中边的规模，纵轴为scd算法在相应网络中进行社团挖掘所需的执行时间。图6表明当网络中边的数量不断增加时，scd算法的执行时间近似呈线性增长，因而可以认定scd算法具有更好的并行化性能，其执行时间随着网络规模的增长具有很好的可扩展性。

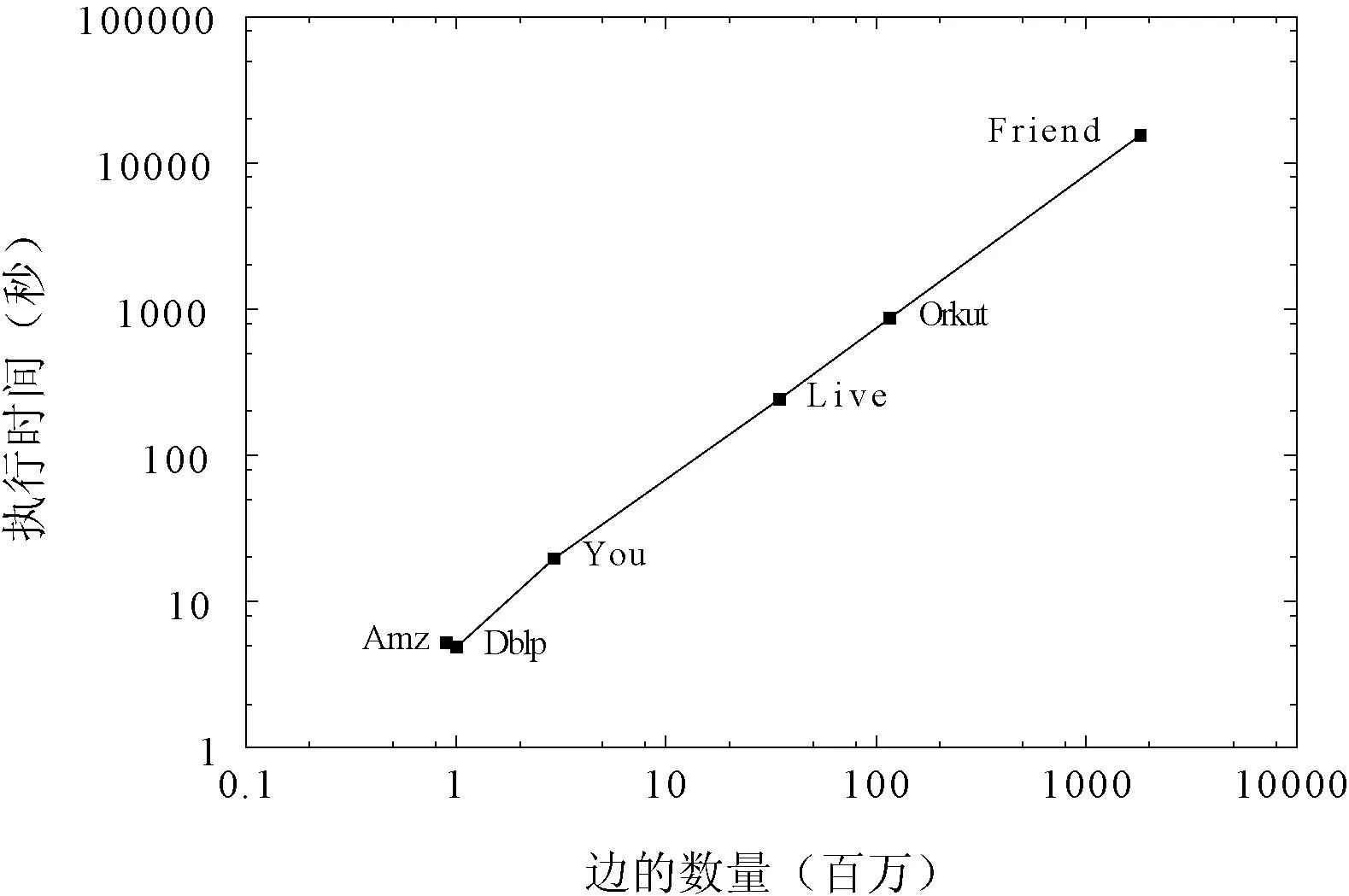
图6　scd算法的可扩展性分析

3结语

社团挖掘是复杂网络的重要研究内容之一。通过社团检测，可以深入了解网络的结构信息，网络中节点之间的交互关系，以及节点在网络的进化中起到的作用。为了减小社团变化带来的WCC计算量，本文提出了一种并行可扩展的社团挖掘算法。对应用WCC进行社团评价的方法进行了分析，提出了一种包含预处理、初始划分和划分改进三个阶段的并行社团挖掘算法。在划分改进中，由于每次社团变化都需要计算大量的WCC提升，本文基于社团的统计量提出一种WCC近似计算方法。大量的真实数据集实验表明，本文提出的社团挖掘算法与相关算法相比较，不仅社团检测的准确性更高，而且具有更好的并行可扩展性。

参考文献

[1] 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].清华大学出版社有限公司,2006.

[2]BoccalettiS,LatoraV,MorenoY,etal.Complexnetworks:Structureanddynamics[J].Physicsreports,2006,424(4):175-308.

[3] 骆志刚,丁凡,蒋晓舟,等.复杂网络社团发现算法研究新进展[J].国防科技大学学报,2011,33(1):47-52.

[4] 汪小帆.复杂网络中的社团结构分析算法研究综述[J].复杂系统与复杂性科学,2005,2(3):1-12.

[5] 王林,戴冠中.基于复杂网络社区结构的论坛热点主题发现[J].计算机工程,2008,34(11):214-216.

[6] 吕金虎.复杂网络的同步:理论,方法,应用与展望[J].力学进展,2008,38(6):713-722.

[7]YangJ,LeskovecJ.Overlappingcommunitydetectionatscale:anonnegativematrixfactorizationapproach[C]//ProceedingsofthesixthACMinternationalconferenceonWebsearchanddatamining.ACM,2013:587-596.

[8]BlondelVD,GuillaumeJL,LambiotteR,etal.Fastunfoldingofcommunitiesinlargenetworks[J].JournalofStatisticalMechanics:TheoryandExperiment,2008,28(10):100-108.

[9]AhnYY,BagrowJP,LehmannS.Linkcommunitiesrevealmultiscalecomplexityinnetworks[J].Nature,2010,466(7307):761-764.

[10]BagrowJP.Communitiesandbottlenecks:Treesandtreelikenetworkshavehighmodularity[J].PhysicalReviewE,2012,85(6):66-78.

[11]FortunatoS,BarthelemyM.Resolutionlimitincommunitydetection[J].ProceedingsoftheNationalAcademyofSciences,2007,104(1):36-41.

[12]LancichinettiA,FortunatoS.Communitydetectionalgorithms:acomparativeanalysis[J].PhysicalreviewE,2009,80(5):056117.

[13]Prat-PérezA,Dominguez-SalD,BrunatJM,etal.Shapingcommunitiesoutoftriangles[C]//Proceedingsofthe21stACMinternationalconferenceonInformationandknowledgemanagement.ACM,2012:1677-1681.

[14]LancichinettiA,FortunatoS,KertészJ.Detectingtheoverlappingandhierarchicalcommunitystructureincomplexnetworks[J].NewJournalofPhysics,2009,11(3):33-45.

WCC-BASED PARALLEL AND SCALABLE COMMUNITY MINING ALGORITHMINCOMPLEXNETWORKS

Yasen·Aizezi1Li Weiping2Guo Wenqiang3

1(Department of Information Security and Engineering,Xinjiang Police College,Urumqi 830013,Xinjiang,China)2(Department of Police Technology,Railway Police College,Zhengzhou 450053,Henan,China)3(School of Computer Science and Engineering,Xinjiang University of Finance and Economic, Urumqi 830013,Xinjiang,China)

AbstractWeighted community clustering (WCC) evaluates the performance of community mining algorithms according to triangles number of a community in complex networks. In primitive WCC algorithm it has the need to compute WCC scores for all community changes in each iteration, therefore the computation burden is very heavy. In order to minimise WCC computation brought about by communities change, this paper proposes a parallel and scalable community mining algorithm. We analysed the methods of community evaluation using WCC, and proposed a parallel community mining algorithm including three stages of preprocessing, initial partitioning and partition refinement. During the process of partition refinement, since every change in community needs much computation for WCC improvements, so we proposed a WCC approximated computation algorithm based on the statistics of community. Massive experiments on real datasets show that, the proposed community mining algorithm is more accurate and has better scalability than related works.

KeywordsComplex networksCommunity miningParallel algorithmScalability

收稿日期：2014-12-02。国家自然科学基金项目(61163066，6090 2074)；新疆维吾尔自治区高校科研计划科学研究重点项目(XJEDU 2013134)；国家社会科学基金项目(13CFX055)；河南省教育厅科学技术研究重点项目(14A520011)。亚森·艾则孜，教授，主研领域：信息安全，自然语言处理，信息检索。李卫平，副教授。郭文强，教授。

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.009