不稳定场对磁共振信号影响分析

苏　晋，　袁小燕，　刘小利，　石春花

(1.长治医学院 基础医学院， 山西 长治　046000;2.长治医学院 生物医学工程系， 山西 长治　046000)



不稳定场对磁共振信号影响分析

苏晋1，袁小燕1，刘小利1，石春花2

(1.长治医学院 基础医学院， 山西 长治046000;2.长治医学院 生物医学工程系， 山西 长治046000)

摘要：利用Bloch方程，选择适当的参数，通过数值模拟的方法详细讨论了主磁场随时间的变化以及涡流对射频场的扰动环境下，磁共振信号随时间的变化情况，为临床磁共振成像技术的应用提供了理论参考。

关键词：磁共振成像； Bloch方程； 不稳定磁场； 磁共振信号

0引言

磁共振成像中，主磁场的稳定性和均匀性、射频场的稳定性以及涡流等因素会影响到图像处理过程，并最终影响到图像质量。造成磁场扰动的因素很多，除了主磁场的稳定性之外，射频场与植入人体内的金属物有相互作用，根据法拉第电磁感应原理，变化的磁场会使得闭合的导体产生电流，从而产生涡流，它一方面会产生热效应[1]，但对人体影响很小，另一方面闭合线圈内的涡流所产生的信号，也会对磁共振图像带来伪影。其中植入人体内的金属物品，包括外科和介入治疗过程中用到人工血管、假牙、血管夹，以及一些电子植入器件如心脏起搏器、骨增长刺激器等[2-4]，之前的研究中，射频场导致的涡流大多是定性的和实验性的讨论，较少提到它对磁共振信号的具体影响。为了定量分析，以下讨论了主磁场随时扰动下，以及涡流对射频场在时间上的扰动情况下对磁共振信号的影响。

1Bloch方程的形式和应用

磁共振成像具有空间分辨率高、无电离辐射、多参数成像等优点[5]。Bloch方程描述了在主磁场和射频场作用下，磁化强度矢量随时间演化的动力学行为，是经典力学描述磁共振现象的重要理论基础之一。布洛赫假设，磁化强度矢量M的运动受到两种力的支配，一种是磁力矩的作用，另一种是弛豫力，在实验室坐标系下，磁化强度矢量M随时变化方程如下[6]：

式中:γ----旋磁比;

M0----主磁场B0中热平衡状态时磁化强度矢量的大小。

Bloch方程的求解较为复杂，直接求解很难得到精确结果，一般采用数值求解的方法来研究具体模型。下面具体讨论不稳定磁场环境下磁共振信号的变化规律。

2稳定均匀的主磁场环境

理想的情况为主磁场在空间和时间上都是均匀分布的。磁共振的信号是在射频脉冲的激励下生成，考虑在90°脉冲作用下磁共振信号随时变化情况，具体参数选择为：B0=1.0T，T1=1.0 s，T2=0.1 s，B1=0.001T，M0=0.02 A/m，其中B0为主磁场强度大小，B1为射频脉冲磁场分量的幅值大小，T1，T2分别为纵向和横向驰豫时间，对生物组织来说，纵向弛豫时间在100 ms到1 s，横向驰豫时间在50～100 ms的范围，如一个特斯拉的磁场中肌肉的横向和纵向驰豫时间分别为750 ms和50 ms左右[7]。这里选择T1=1.0 s，T2=0.1 s。

根据Bloch方程，通过直接求解一阶微分方程组，得到磁共振信号在上述条件下随时演化情况，如图1所示。

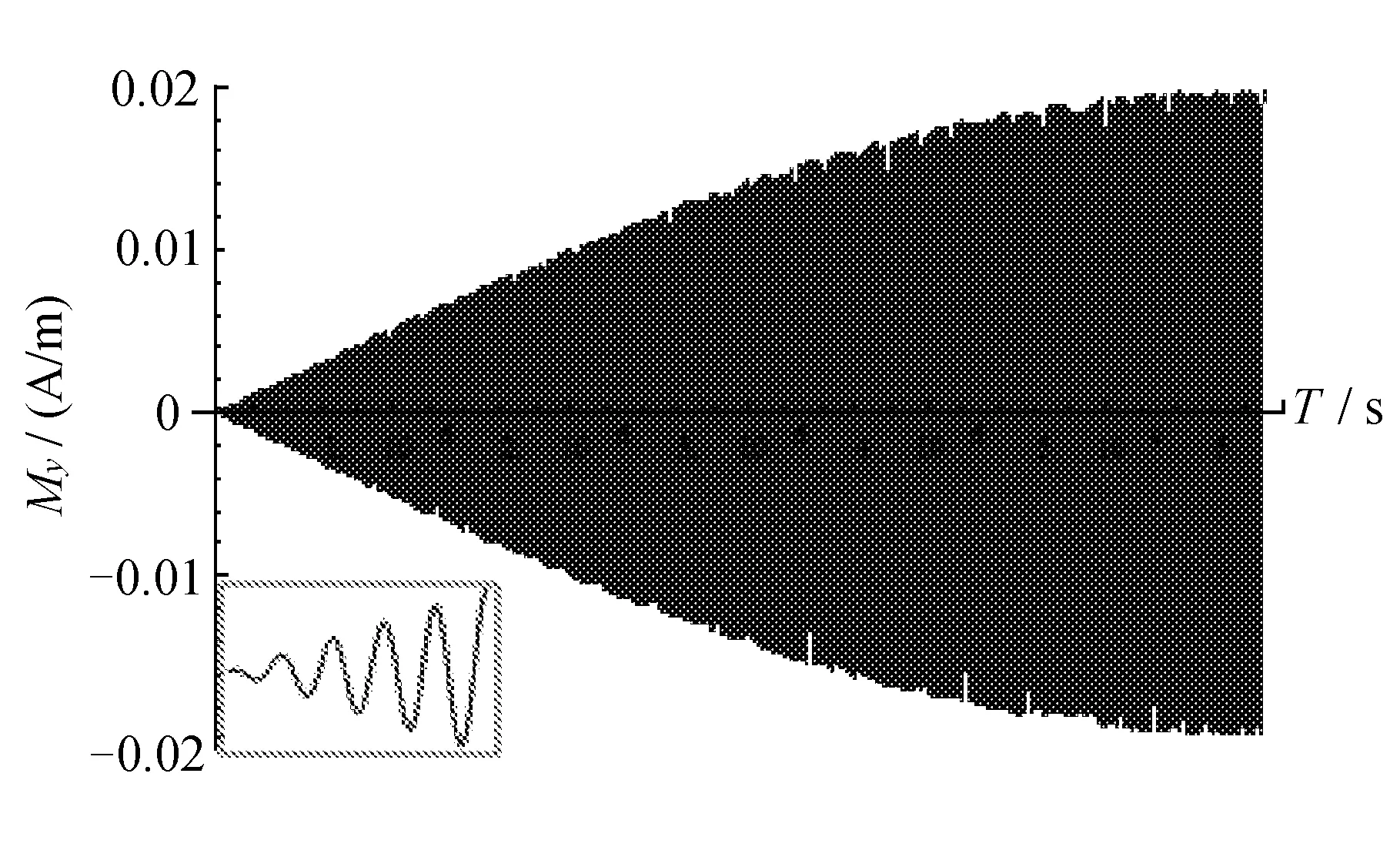
图1　90°脉冲作用下磁化强度矢量M在y方向投影值的变化

在90°射频脉冲作用下，图1显示了直角坐标系下磁化强度矢量M沿y方向的分量My(t)，它反映了磁共振信号随时间的变化情况。显然My(t)随着时间的变化不断振荡，同时逐渐增大，由于频率较高，所以图像比较密集，图中左下为t=0～1.2×10-7s时间段的局部放大图，同时这与M由主磁场B0方向偏转到xy平面的过程相对应,它反映了信号随时变化趋势。

3主磁场随时扰动情况对磁共振信号的影响

磁共振成像中，受磁体所处的环境或者匀强线圈漂移的影响，磁场的稳定会发生变化，所以，磁场的均匀性是磁共振成像的一个重要指标。主磁场B0(设为直角坐标系下z方向)不均匀意味着不同空间位置的自旋质子旋进频率不一样，造成了质子的自旋磁矩之间相位不一致，从而减弱磁共振信号。在磁共振成像设备中，主磁场的不均匀性通常随空间位置的变化被讨论的较多[8-9]。磁场随时间的变化同样会加剧自旋磁矩的分布，影响磁共振信号的大小。为研究方便，设在射频脉冲作用期间，随时间周期性变化的幅度很小磁场叠加在主磁场中，并考虑其对磁共振信号的影响。

设定主磁场为:

Bz=B0+kB0cos(ωt)

式中：kB0cos(ωt)----随时间扰动的磁场分量；

ω----扰动频率；

k----叠加在扰动场的幅度值，通常很小，这里选择k=0.001。

频率选择

式中:B1----射频脉冲磁场分量的幅值。

磁化强度矢量M在xy平面投影的大小如图2所示。

从图中可以看到，含时微扰下的主磁场环境中，磁化强度矢量在xy平面的分量相对较小，这也反映出磁共振信号会在不稳定的主磁场中出现信号衰减的情况。从幅度上看，这种衰减很小。在变化趋势上，90°脉冲作用期间的中末期阶段衰减较多。另外，从数值计算的结果来看，含时微扰场的频率较大时，其对磁共振信号的影响较小，尤其是接近磁共振频率时，几乎没有影响。

4RF脉冲场不均匀对磁共振信号的影响

在一般的情况下，射频场的不均匀和涡流的产生也会影响到磁共振信号的稳定性，如在高场和超高场的环境下[10]。射频场的不均匀被讨论的较多[11-12]，而涡流的产生对磁共振信号的影响较少被提及，为了定量讨论其影响，设定磁场环境为[13]：

主磁场:

脉冲射频场:

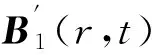
它表示在磁共振成像区域中，射频脉冲作用时，由于金属物体的存在，导致涡流的出现，同时也激励出与射频脉冲频率相同的电磁波分量。为了讨论方便，不考虑主磁场和射频场的均匀性问题，仅对射频扰动场的影响进行讨论，其它参数不变。设u1=9.1×10-4,u2=1.1×10-3,v1=5×10-4,v2=8.3×10-4。

磁化强度矢量M在xy平面分量的模的平方，在90°射频脉冲作用随时间的变化趋势如图3所示。

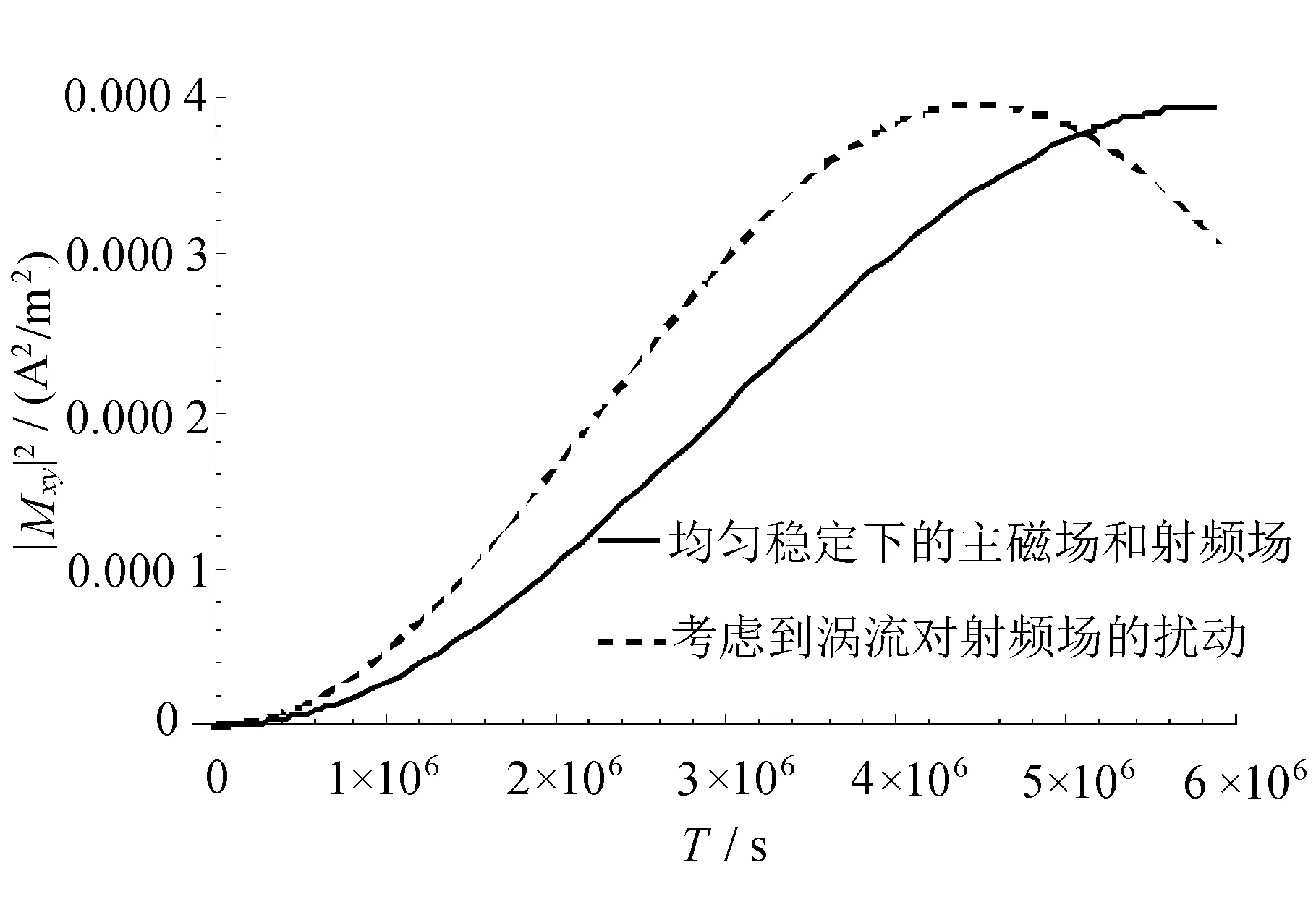
图3　涡流对射频场扰动下|Mxy|2随时间的变化

从数值模拟结果来看，90°脉冲作用期间，|Mxy|2会逐渐增加，涡流对射频场的扰动(虚线所示)导致|Mxy|2变化率也增加，比同一时间下的稳定射频场环境也有了更大的|Mxy|2值。而在射频脉冲结束前的一小段时间开始逐渐减小，90°脉冲结束时，|Mxy|2变小。这表明在选择脉冲序列产生磁共振信号时，如果考虑到涡流的影响，相同的脉宽作用下，磁共振信号会有所不同，这个结论为初始磁化强度矢量的正确选择提供了理论参考。

5结语

磁共振信号在不稳定的磁场环境中，主要考虑主磁场不稳定以及涡流对射频场不均匀的影响，分析了其在90°脉冲作用下，磁化强度矢量的变化情况。结果显示，一方面，主磁场的不稳定将会减弱磁化强度矢量在xy平面的分量，从而减弱磁共振信号，但这种影响较小，因为实际情况中扰动场幅度很小，同时从数值模拟的结果来看，扰动场的频率较高时，比如接近磁共振频率范围时，几乎没有影响。另一方面，涡流对射频场的影响导致相同的脉宽作用下，会产生不同的Mxy分量，从而得到不同的磁共振信号的初始值，如在脉冲作用期间Mxy会增大，而在脉冲作用末期会减小。这些变化规律为临床磁共振成像终脉冲序列的设计和应用提供了理论参考。

参考文献：

[1]马超,褚旭,李烨,等.磁共振成像中涡流效应的仿真[J].清华大学学报:自然科学版,2007,47(4):457-461.

[2]贺李,余深平,孟悛非.金属物对磁共振检查的影响及相关研究进展[J].国际医学放射学杂志,2009,32(1):53-57.

[3]杨长伟,李明,魏显招.矫形外科金属植入物磁共振成像伪影分析专用水模:CN202505350U[P].2012.

[4]王传兵,邹月芬,储斌.磁共振场强及序列选择对金属植入物伪影大小影响探讨[J].生物医学工程与临床,2014(1):5-9.

[5]潘洪凯.新型磁共振成像造影剂的合成及性质研究[D].长春:长春工业大学,2012.

[6]吉强.医学影像物理学[M].北京:人民卫生出版社,2010:82.

[7]Hendee W R, Ritenour E R. Medical imaging physics[J]. Fourth Edition Medical Physics,2003,30(4):730-730.

[8]骆国丽,肖亮.主磁场不均匀情况下的磁共振虚拟成像初步研究[J].磁共振成像,2015(6):471-475.

[9]彭玺.参考制导的快速磁共振成像和场不均匀性修正[D].武汉:武汉大学,2012:74-80.

[10]Yulin, Robert, Grossman,等.超高场MRI:脑部成像结果探讨[J].磁共振成像,2010(3):169-176.

[11]蒋瑞瑞.磁共振脉冲优化设计[D].长春:中国科学院研究生院(长春光学精密机械与物理研究所),2013:20-21.

[12]邵汀汀.高场磁共振下并行激发技术的相关研究[D].杭州:浙江大学,2012:10.

[13]Balac S, Chupin L. Fast approximate solution of Bloch equation for simulation of RF artifacts in magnetic resonance imaging[J]. Mathematical & Computer Modelling,2008,48(11/12):1901-1913.

Influence of unstable field on MRI signal

SU Jin1,YUAN Xiaoyan1,LIU Xiaoli1,SHI Chunhua2

(1.College of Basic Medical, Changzhi Medical College, Changzhi 046000, China;2.Department of Biomedicine Engineering, Changzhi Medical College, Changzhi 046000, China)

Abstract：Bloch equation is applied to study the change of MRI signal with time by means of numerical simulation, considering main magnetic field variation and eddy induced RF field. The results can offer some theoretic reference for MRI application.

Key words：MRI; Bloch equation; unstability field; MRI signal.

收稿日期：2016-01-25

基金项目：山西省高校科技开发项目(20091025)； 2015年长治医学院博士启动基金项目(BS15015); 长治医学院科研启动基金项目(QDZ201530)

作者简介：苏晋(1980-)，男，汉族，山西长治人，长治医学院讲师,硕士，主要从事理论物理方向研究,E-mail:littlesujin@163.com.

DOI:10.15923/j.cnki.cn22-1382/t.2016.3.13

中图分类号：O 571.22

文献标志码：A

文章编号：1674-1374(2016)03-0273-04