几何公差状态向量模型及其分析与综合技术*

刘伟东　涂玉婷　刘海明

(1.华南理工大学 自动化科学与工程学院, 广东 广州 510640; 2.广东省农业科学院, 广东 广州 510640)



几何公差状态向量模型及其分析与综合技术*

刘伟东1涂玉婷2刘海明1

(1.华南理工大学 自动化科学与工程学院, 广东 广州 510640; 2.广东省农业科学院, 广东 广州 510640)

摘要:在产品零件装配互换性设计中,几何公差的分析与综合技术发展还不完善.文中针对几何公差分析与综合的问题,提出了几何公差的状态向量表示模型;基于几何公差的状态向量表示对几何偏差作用和偏差累积进行了分析,给出了在零件不同配合状态下的装配功能几何变动的状态向量表达,并在此基础上给出了几何公差分析与综合的状态方程;最后以多舱段对接装配为实例给出了基于状态方程的几何公差分析与综合的算法步骤.实例结果验证了几何公差状态向量表示模型及其状态方程对几何公差分析与综合的有效性和适用性.

关键词：几何公差;状态向量模型;公差分析；公差综合;配合和公差

几何公差包括几何位置公差和几何形状公差,前者用于约束几何位置的变动,如平行度、垂直度等,后者用于约束几何形状的变动,如直线度、圆柱度等.传统的公差分析与综合通常只涉及尺寸公差的分析与综合问题,没有讨论几何公差的分析与综合问题.几何公差的分析与综合是相对尺寸公差的分析与综合提出来的,是对尺寸公差分析与综合的拓展.几何公差分析主要是根据已知的公差几何、公差类型、公差域、公差基准和公差条件信息求解受几何公差影响的装配功能要求;几何公差综合是根据已知的装配功能要求设计和求解公差几何、公差类型、公差域、公差基准和公差条件信息.几何公差分析与综合的指标包括装配功能要求、装配成功率、加工和装配保证成本等.目前,几何公差分析与综合问题的研究没有形成比较系统的模型或理论,国内外学者在几何偏差向量[1- 3]、公差图[4- 5]、几何变动模型[6- 10]、装配建模[11]等方面进行了研究.几何变动模型主要用于几何形状公差的表达,而几何偏差向量主要用于几何位置公差的表达.无论是几何变动模型还是几何偏差向量,在计算机辅助几何公差分析与综合应用方面,都具有一定的局限性.

在几何公差分析与综合方法中,智能控制技术的应用还比较少,主要是基于特定尺寸链模型来对尺寸公差分析或综合指标进行智能优化,如遗传算法[12]、蚁群算法[13]等;而其他非线性控制方法,如鲁棒控制、自适应控制、学习控制、神经网络控制等涉及的比较少.由于非线性智能控制方法几乎能对各类非线性进行一致稳定的逼近,且能很好地处理内部和外部不确定,因此,文中旨在将非线性智能控制算法应用于几何公差的分析和综合,探讨几何公差分析与综合的智能化方法.

1几何公差表达

在互换性理论中,几何位置公差要素包括公差几何、公差类型、公差域、公差基准和公差要求等,几何形状公差要素包括公差几何、公差类型、公差域和公差要求等[14].为了使表达模型统一,几何公差用状态向量表达为

θ=(θ1,θ2,θ3,θ4,θ5)T

(1)

式中:θ1∈Ω1为公差几何标定,Ω1为几何指标(ID)集,在实体建模时构建;θ2∈Ω2为公差类型标定,Ω2为公差类型标定集,根据国际标准化组织(ISO)标准共有14类;θ3∈Ω3为公差域标定,Ω3为公差域ID集,公差域需要专门的建模并分配ID;θ4∈Ω1为公差基准标定;θ5∈Ω5为公差要求标定,Ω5为公差要求标定集,根据ISO标准共有3类.

对于几何公差状态向量θ,在公共坐标系下,公差约束几何的变动记为

f(θ2)=CMδ

(2)

式中,δ为几何三移动三转动方向的局部变动,δ=(δx,δy,δz,δα,δβ,δγ)T，Mδ为公差几何相对基准几何的变动,C为基准几何到公共坐标系的坐标变换,M为与公差类型θ2有关的约束矩阵[15].

2几何偏差的作用和偏差累积

在产品装配过程中,几何偏差的作用和偏差累积主要包含两类:①零件内两特征之间的偏差作用,主要指同一零件内一功能几何偏差对另一功能几何的影响；②两零件不同特征之间的偏差作用,主要指零件内一功能几何偏差对另一零件内一功能几何的影响.

计算一个或多个零件之间的这两类偏差作用,并进行偏差作用的累积分析,可以实现产品的关键和最终装配功能要求的分析,以及基于累积模型的几何公差的分析与综合.

2.1零件内两特征之间的偏差作用

对于零件p内两特征之间的偏差作用,记一功能几何i的几何公差状态向量为

θpik=(θpik1,θpik2,θpik3,θpik4,θpik5)T,

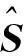
(3)

对于同一零件p内功能几何i的ni个几何公差,其基于极值法的几何偏差综合作用为

(4)

考虑功能几何j自身的几何偏差,记其几何公差状态向量为θpjk1=(θpjk11,θpjk12,θpjk13,θpjk14,θpjk15)T,其中,k1=1,2,…,nj(nj为功能几何j的几何公差数),则考虑零件p内功能几何i的几何公差的影响时,功能几何j的几何公差状态向量变为

(5)

f(θpjnj2))T.

2.2两零件不同特征之间的偏差作用

记两零件p、q的配合几何分别为s和t,零件p内配合几何s的几何公差状态向量为θpsk2=(θpsk21,θpsk22,θpsk23,θpsk24,θpsk25)T,其中,k2=1,2,…,ns(ns为配合几何s的几何公差数),则根据零件内两特征之间的偏差作用公式(5),考虑零件p内功能几何i的变动时,配合几何s的几何公差状态向量变为

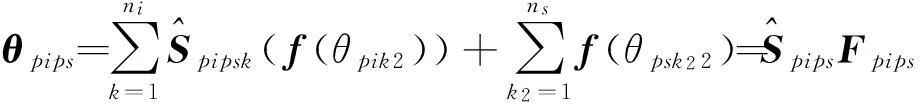
记零件q内配合几何t的几何公差状态向量为θqtk3=(θqtk31,θqtk32,θqtk33,θqtk34,θqtk35)T,其中k3=1,2,…,nt(nt为配合几何t的几何公差数).再考虑零件q内功能几何j的几何公差状态向量θqjk1=(θqjk11,θqjk12,θqjk13,θqjk14,θqjk15)T,其中,k1=1,2,…,nj(nj为功能几何j的几何公差数).根据零件内两特征之间的偏差作用公式(5),考虑零件q内功能几何j的变动时,配合几何t的几何公差状态向量变为

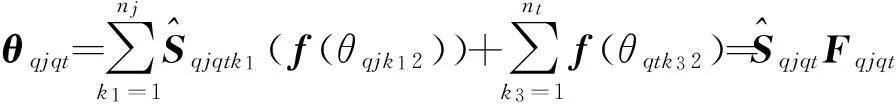
(f(θqj12), f(θqj22),…, f(θqjnj2), f(θqt12), f(θqt22),…, f(θqtnt2))T.

进一步地,考虑零件p和q的配合关系,有

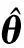
(6)

2)当零件p和q为接触配合时,零件p内配合几何s的几何公差状态向量会直接引起零件q的装配变动,以及影响功能几何j的几何公差状态.考虑配合几何s的几何公差状态向量时,零件q内功能几何j的几何公差状态向量变为

(7)

为统一描述两零件在不同配合状态下的偏差作用,文中引入配合状态变量w(s,t)和投影算子P(w):

(8)

当配合状态为间隙配合时,w(s,t)=0;当配合状态为接触配合时,w(s,t)=1.考虑两零件不同特征之间的偏差作用时,零件q内功能几何j的几何公差状态向量可统一表达为

(9)

3几何公差分析与综合的状态方程

3.1配合通路对装配功能要求的作用

考虑配合通路r[15]:wr(sp1,tq1)→wr(sp2,tq2)→…→wr(spNr,tqNr),其中,r为配合通路序号,Nr为配合通路r的配合数;spm(m=1,2,…,Nr)为零件pm的配合公差几何,tqm为零件qm的配合公差几何,且有qm=pm+1,即零件qm和pm+1为同一零件.则考虑配合wr(spm,tqm)的作用时,由式(9)可得零件pm+1的功能几何spm+1的几何公差状态向量表达式:

(10)

考虑配合wr(spm,tqm)和wr(spm+1,tqm+1)的作用,由式(9)可得零件pm+2的功能几何spm+2的几何公差状态向量表达式:

θspm+2=P(wr(spm+1,tqm+1))+

(11)

P(wr(spm+1,tqm+1))=

(12)

因此,考虑配合wr(sp1,tq1)到wr(spNr,tqNr)的作用,由式(9)可得零件qNr内功能几何sqNr的几何公差状态向量表达式:

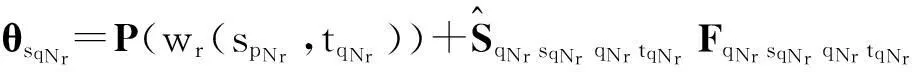
假定存在M条配合通路会对装配体某零件内装配功能几何yd=sqNr的几何公差状态产生影响,则装配功能几何yd的几何公差状态向量可表示为

(13)

3.2零件内特征对装配功能要求的作用

假定装配功能几何yd所属零件为pyd,现分析零件pyd内其他几何或特征几何公差对装配功能几何yd的作用.考虑零件pyd内公差几何h,记其几何公差状态向量为θpydhk4=(θpydhk41,θpydhk42,θpydhk43,θpydhk44,θpydhk45)T,其中,k4=1,2,…，nh(nh为h的几何公差数).则由式(3)可得几何偏差f(θpydhk42)对同一零件pyd内装配功能几何yd的作用为

(14)

对于同一零件pyd内功能几何h的nh个几何公差,由式(4)得到其几何偏差综合作用为

(15)

Fydh=(f(θpydh12), f(θpydh22),…， f(θpydhnh2))T.

假定零件pyd内存在H个几何或特征会对装配功能几何yd的几何公差状态产生影响,则考虑零件pyd内公差几何的影响,装配功能几何yd的几何公差状态向量为

(16)

3.3装配功能几何综合公差状态向量

同时考虑各配合通路和零件pyd内各公差几何的作用,将其代入式(13)和(16)得到装配功能几何yd的几何公差状态向量为

(17)

3.4状态方程

假定某一特定装配功能设计要求的几何公差状态向量描述为

θyd=(θy1,θy2,θy3,θy4,θy5)T

(18)

则几何公差分析与综合的状态方程可描述为

(19)

式中,x=(θy1,θy2,θy3,θy4,θy5)T为状态变量,y为输出变量,u为输入变量,S(u)为u的灵敏度矩阵函数,Δ(u)为u的不确定函数.

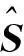
ε=f(θy2)-[S(θyd)θyd+Δ(θyd)]→0.

4状态方程的应用及实例

文中以文献[16]描述的航天器多个舱段对接精度计算为例来介绍状态方程(19)的构建过程.假设舱段个数为4,各舱段连接方式为对接,对接端面示意图如图1所示.

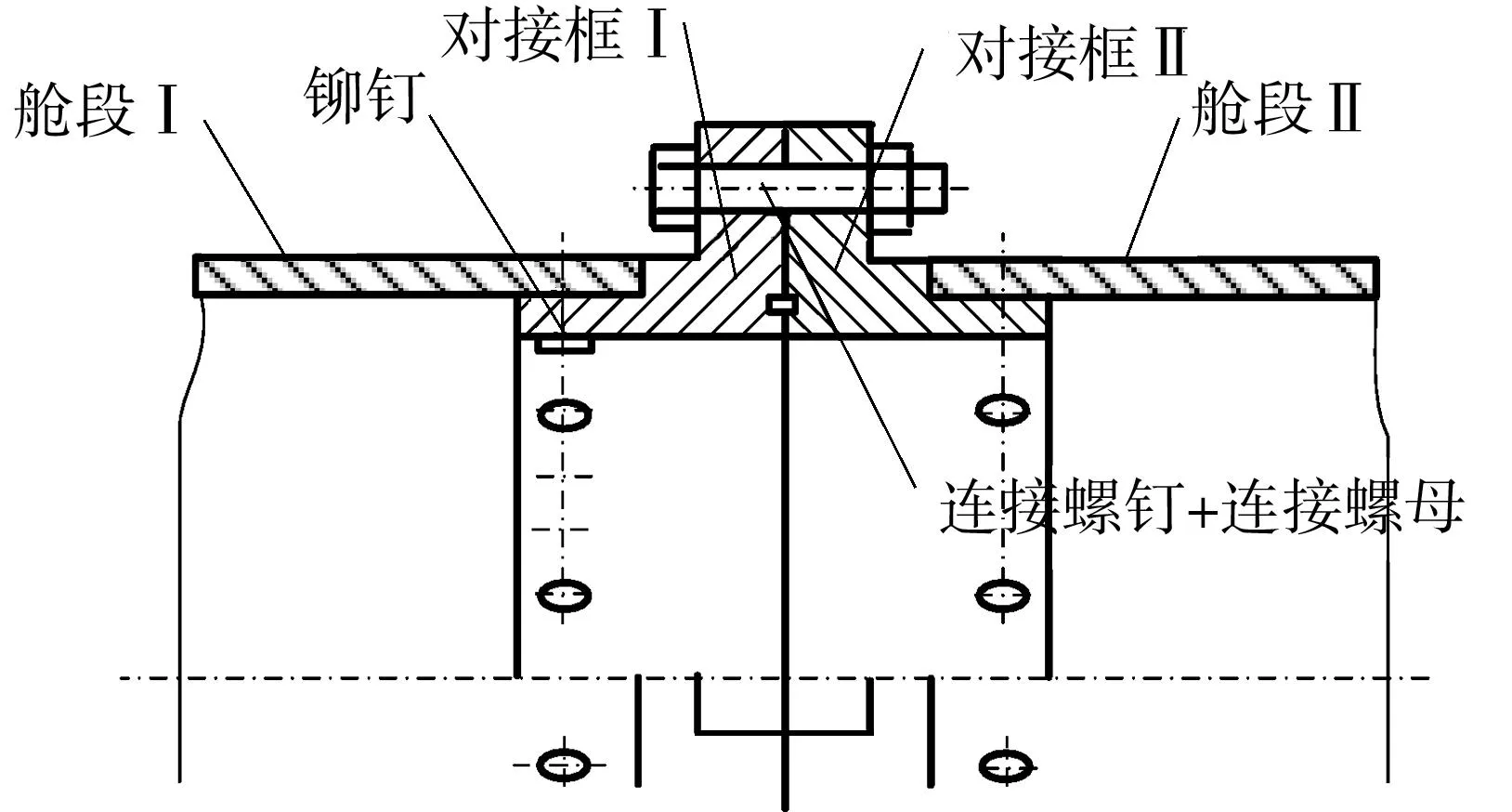
图1　某两舱段航天器的对接端面示意图

Fig.1Schematic diagram of end faces docking for a 2-cabin spacecraft

影响两舱段对接精度的因素有铆接孔位置度、连接紧固件与孔的配合偏差(包括孔上差、紧固件下差)、前后舱段对接框端面垂直度及直径等.为了简化计算,假定铆接孔位置度、前后舱段对接框端面垂直度已知,同时忽略端面表面粗糙度的影响,只针对对接孔上差、紧固件下差进行设计.4个对接舱段的端面连接示意图如图2所示.

设各舱段编号为pk′(k′=1,2,3,4);4个舱段构成3组对接结构,各对接编号为wi′(i′=1,2,3);每组对接包含6个对接孔和对接轴,孔上差为ai′1,紧固件下差为ai′2,分度圆半径ri′=185 mm,各舱段长lk′=1 573 mm.由于每组对接孔上差、紧固件下差的影响,舱段连接wi′会在圆周方向产生扭转变动Δαi′和在径向产生同轴度变动Δγi′.4个舱段最终的装配功能要求为:舱段p1外圆柱面g13相对舱段p4外圆柱面g43的扭转变动为Δα,舱段p1轴线g15相对舱段p4轴线g45的同轴度变动为Δγ.参照文献[15],各组舱段对接wi′的几何公差约束矩阵和几何变动向量计算如表1所示,其中,δxai′1、δxai′2和δxΔγi′为对接局部坐标系下沿x方向的绝对几何变动量,δyai′1、δyai′2和δyΔγi′为对接局部坐标系下沿y方向的绝对几何变动量,δαai′1、δαai′2和δαΔγi′为对接局部坐标系下绕x轴的绝对几何变动量,δβai′1、δβai′2和δβΔγi′为对接局部坐标系下绕y轴的绝对几何变动量,δγΔαi′为对接局部坐标系下绕z轴的绝对几何变动量,坐标系方向如图2所示.

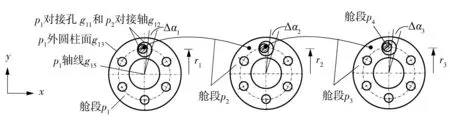
图2　某4个舱段航天器的对接端面示意图

Table 1Constraint matrix and geometric deviation vector for geometry tolerance

几何公差约束矩阵公差几何变动向量ai'1diag(1,1,0,1,1,0)(δxai'1,δyai'1),0,δαai'1,δβai'1,0)Tai'2diag(1,1,0,1,1,0)(δxai'2,δyai'2),0,δαai'2,δβai'2,0)TΔαi'diag(0,0,0,0,0,1)(0,0,0,0,0,δγΔαi')TΔγi'diag(1,1,0,1,1,0)(δxΔγi',δyΔγi',0,δαΔγi',δβΔγi',0)T

4.1偏差作用与几何公差分析

对于图2所示第i组舱段对接wi′,假设已知孔上差ai′1=0.1 mm、紧固件下差ai′2=-0.03 mm;影响舱段最终扭转变动Δγ、同轴度变动Δα的配合通路为wr(g11,g12)→wr(g21,g22)→wr(g31,g32),其中gi′1和gi′2为配合几何标定.由式(17)可得舱段p1外圆柱面g13与舱段p4外圆柱面g43在圆周方向的偏差作用:

θ=P(wr(g31,g32))+θg32g43

(20)

其中,P(wr(g31,g32))=

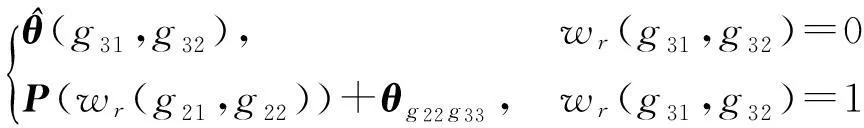
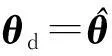
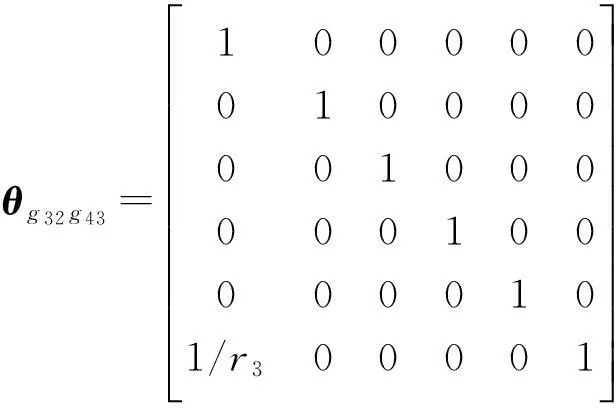
(δxa32,δya32,0,δαt32,δβt32,0)T=

(δxa32,δya32,0,δxa32/l4,δβa32/l4,δxa32/r4)T=

(0.03,0.03,0,1.9×10-5，1.9×10-5，

1.6×10-4)T.

当wr(g31,g32)=1时,代入两零件不同特征之间的偏差作用见式(9)和(5)),得

θΔγd=P(wr(g21,g22))+θg22g33+θ(g32g43),

其中,θg22g33为对接轴g22对轴舱段外圆柱面g33的作用,根据零件内两特征间偏差作用(见式(6)),有

θg22g33=(δxa22,δya22,0,δxa22/l3,δβa22/l3,δxa22/r3)T=(0.03,0,0.3,0,1.9×10-5,1.9×10-5,1.6×10-4)T.

当所有的wr(gi 1,gi 2)=1时,代入式(9)和(5),得

θd=θg11g13+θg12g23+θg22g33+θg32g43

(21)

式中:θg11g13为对接轴线g11对舱段外圆柱面g13的作用,根据零件内两特征间的偏差作用(见式(6)),有

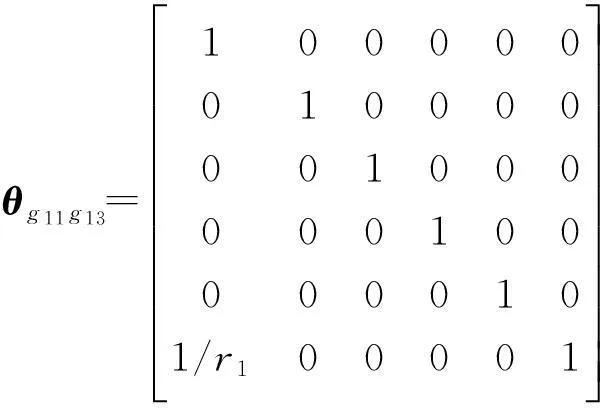
(δxa11,δya11,0,δαa11,δβa11,0)T=

(δxa11,δya11,0,δxa11/l1,δβa11/l1,δxa11/r1)T=

(0.1,0.1,1.0,6.5×10-5，6.5×10-5，5.4×10-3);θg12g23为对接轴线g12对舱段外圆柱面g23的作用,根据零件内两特征间偏差作用(见式(6)),有

θg12g23=(δxa12,δya12,0,δxa12/l2,δβa12/l2,δxa12/r2)T=

(0.03,0.03,0.1,1.9×10-5，1.9×10-5，1.6×10-4)T，

代入式(21)得θd=(0.19,0.19,0,1.2×10-4,1.2×10-4,5.9×10-3)T.

此时,舱段p1外圆柱面g13相对舱段p4外圆柱面g43的扭转变动Δα=5.9×10-3rad,舱段轴线相对舱段轴线的同轴度变动Δγ=0.19 mm.

4.2装配功能状态方程与几何公差综合

假设要求的最终装配扭转变动Δα=0.006 rad,同轴度变动Δγ=0.2 mm,则可以构建扭转变动对应的目标公差状态向量:θΔα=(g13,c32,d33,g43,e34)T,其中,c32为扭转装配功能,e34为无公差要求,d33为扭转公差域Ωδ3:={δ3∶0≤δγΔα≤0.006}.

由式(19)得到最终装配扭转变动Δα的输入输出状态方程为

(22)

式中,xα为状态变量,yα为输出变量,uα为输入变量.则yα在圆周方向的Δα的期望值为fd(c32)=(0,0,0,0,0,δγΔγ)T.Δα的几何公差综合的途径是:基于状态方程式(22),设计智能非线性控制器u(θΔαd)和自适应律ua(θΔαd),使误差

εα=fd(c32)-[S(θΔαd)θΔαd+Δ(θΔαd)]→0.

同理,同轴度变动Δγ的几何公差综合的途径是:基于Δγ的输入输出状态方程,设计智能非线性控制器u(θΔγd)和自适应律ua(θΔγd),使误差

εγ=fd(c33)-[S(θΔγd)θΔγd+Δ(θΔγd)]→0.

由舱段对接装配变动分析实例得到基于状态方程的几何公差分析与综合的算法步骤如下:

1)基于装配实体模型构建几何公差表达各要素集Ω,确定各几何公差的状态向量表达模型,并确定几何变动向量、几何公差域变动边界;

2)基于关键或最终装配功能要求确定M条配合通路,确定各通路各配合的配合状态w;

3)从各配合几何出发,计算各个零件内两特征之间的偏差作用、两零件不同特征之间的偏差作用;

4)由式(17)计算最终装配功能要求的几何公差状态向量综合表达,并由式(19)确定关于最终装配功能要求的状态方程;

5)基于最终装配功能要求的状态方程及其期望值设计智能非线性控制器u(θyd)和自适应律ua(θyd),使误差ε=f(θy2)-[S(θyd)θyd+Δ(θyd)]→0.

5结论

参考文献：

[1]LIHai,ZHUHaiping,LIPeigen,etal.Toleranceanalysisofmechanicalassembliesbasedonsmalldisplacementtorsoranddeviationpropagationtheories[J].Interna-tionalJournalofAdvancedManufacturingTechnology,2014,72:89- 99.

[2]MASSIMILIANOM,WILMAP.Areviewoftwomodelsfortoleranceanalysisofanassembly:vectorloopandmatrix[J].InternationalJournalofAdvancedManufacturingTechnology,2009,43:1106- 1123.

[3]SAHANIAK,PRAMODKJ,SATISHCS.Tolerancestackupanalysisforangularityofcomponentsandtheirassembly[J].ProcediaEngineering,2014,69:952- 961.

[4]GAURAVA,JOSEPHKD,JAMIS.Influenceofformontolerance-map-generatedfrequencydistributionsfor1Dclearanceindesign[J].PrecisionEngineering,2010,34:22- 27.

[5]CHENHua,JINSun,LIZhimin,etal.Acomprehensivestudyofthreedimensionaltoleranceanalysismethods[J].Computer-AidedDesign,2014,53:1- 13.

[6]JEANYD,LUCM,ALEXB,etal.Tolerancesynthesis:quantifiernotionandvirtualboundary[J].Computer-AidedDesign,2005,37:231- 240.

[7]BENJAMINS,SANDROW.Adiscretegeometryapproachfortoleranceanalysisofmechanism[J].MechanismandMachineTheory,2014,77:148- 163.

[8]BENJAMINS,NABILA,LUCM,etal.Skinmodelshapes:anewparadigmshiftforgeometricvariationsmodelinginmechanicalengineering[J].Computer-AidedDesign,2014,50:1- 15.

[9]NABILA,BENJAMINS,LUCM,etal.Fromsolidmode-lingtoskinmodelshapes:shiftingparadigmsincompu-teraidedtolerancing[J].CIRPAnnals-ManufacturingTechnology,2014,63:137- 140.

[10]NABILA,ALEXB,LUCM.Theskinmodel,acomprehensivegeometricmodelforengineeringdesign[J].CIRPAnnals-ManufacturingTechnology,2013,62:143- 146.[11]MATHIEUM,MAXG,PASCALH.Anewcalculationmethodfortheworstcasetoleranceanalysisandsynthesisinstack-typeassemblies[J].Computer-AidedDesign,2011,43:1118- 1125.

[12]SINGHPK,JAINPK,JAINSC.Ageneticalgorithm-basedsolutiontooptimaltolerancesynthesisofmechanicalassemblieswithalternativemanufacturingprocesses:focusoncomplextolerancingproblems[J].InternationalJournalofProductionResearch,2004,42(24):5185- 5195.[13]PRABHAHARANG,ASOKANP,RAJENDRANS.Sensitivity-basedconceptualdesignandtoleranceallocationusingthecontinuousantscolonyalgorithm(CACO)[J].InternationalJournalofAdvancedManufacturingTechnology,2005,25:516- 526.

[14]GBT1182—2008,Geometricalproductspecifications(GPS)-geometricaltolerancing-toleranceofform,orientation,locationandrun-out[S].

[15]刘伟东,宁汝新,刘检华,等.基于偏差有向图和DH方法的产品装配精度预测技术 [J].机械工程学报,2012,48(7):125- 140.

LIUWei-dong,NINGRu-xin,LIUJian-hua,etal.Precisionpredictingbasedondirecteddeviationgraphmode-lingandD-Hmethodology[J].ChineseJournalofMechanicalEngineering,2012,48(7):125- 140.

[16]刘伟东,宁汝新,刘检华,等.计算机辅助航天器舱段连接精度计算与分析 [J].计算机集成制造系统,2011,17(4):732- 739.LIUWei-dong,NINGRu-xin,LIUJian-hua,etal.Com-puteraidedanalysisforconnectionprecisionofmissilesection[J].ComputerIntegratedManufacturingSystems,2011,17(4):732- 739.

收稿日期:2015- 10- 19

*基金项目:国家自然科学基金资助项目(51305140);广东省工业高新技术领域科技计划项目(2014A040401019,2015A030401029,2014A010104004)

Foundation items: Supported by the National Natural Science Foundation of China(51305140)and the Science and Technology Planning Project for Industrial High-Technolgoy of Guangdong Province(2014A040401019,2015A030401029,2014A010104004)

作者简介:刘伟东(1984-),男,博士,助理研究员,主要从事智能制造、数字化制造技术下的复杂产品装配精度预分析技术研究.E-mail:aulwd@scut.edu.cn

文章编号:1000- 565X(2016)05- 0078- 06

中图分类号：TP 391.9

doi：10.3969/j.issn.1000-565X.2016.05.012

State Vector Model of Geometry Tolerance and Techniques for Tolerance Analysis and Synthesis

LIUWei-dong1TUYu-ting2LIUHai-ming1

(1.School of Automation Science and Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China;2.Guangdong Academy of Agricultural Science,Guangzhou 510640,Guangdong,China)

Abstract:As the existing interchangeability design process of part assembly is restricted to the imperfect analysis and synthesis techniques of geometric tolerance,firstly,a state vector model of geometric tolerance is proposed.Secondly,the geometric deviation affection and deviation accumulation are analyzed on the basis of the proposed model,respectively.Then,the state vector expression of assembly deviation affection and accumulation is deduced for the parts in different fitting statuses,and a state equation for the geometric tolerance analysis and synthesis is presented.Finally,an end faces docking example of spacecraft cabins is illustrated to explore the process of geometric tolerance analysis and synthesis with the help of the proposed state equation.Example results show that the proposed state vector model and the corresponding state equation are both effective and applicable for geometric tolerance analysis and synthesis.

Key words:geometric tolerance;state vector model;tolerance analysis;tolerance synthesis;fits and tolerances