基于FrFT的自适应宽带干扰抑制算法

刘秉瑞，粟　嘉

(1.中国电子科技集团公司第十五研究所，北京　100083；2.西北工业大学电子信息学院，西安　710072)



工程与应用

基于FrFT的自适应宽带干扰抑制算法

刘秉瑞1，粟嘉2

(1.中国电子科技集团公司第十五研究所，北京100083；2.西北工业大学电子信息学院，西安710072)

摘要：宽带干扰(WBI)的存在将会大幅度地降低合成孔径雷达(SAR)图像的质量。本文在非蓄意WBI线性调频特性的基础上，提出一种基于FrFT自适应宽带干扰抑制方法。该算法首先将SAR回波数据变换到分数阶变换域，在最佳变换域内WBI具有窄带干扰(NBI)的特性，然后采用自适应信号分离算法，在最佳变换域内实现干扰和有用信号的分离。该算法能有效抑制SAR图像中的时变WBI，同时能够尽可能保留有用信号。结合仿真和实测数据的实验分析，验证了本文方法的有效性。

关键词：SAR；干扰抑制；分数阶傅里叶变换；自适应信号分离中图分类号：TN957

文献标识码：A

文章编号：1673-5692(2016)03-319-07

0引言

由于合成孔径雷达(SAR)具有全天时、全天候工作和广域监视等特点，在战场侦察和资源勘探等方面的运用受到越来越广泛的重视。非蓄意干扰是和平时期对地监视模式面临的主要干扰形式之一，对SAR精确遥感技术造成巨大的威胁。根据干扰信号的带宽可以把干扰分为窄带干扰(NBI，带宽小于有用信号带宽的1%)和宽带干扰(WBI，其带宽与信号带宽可比拟)。对地监视模式面临的非蓄意干扰主要来源于其它雷达发射信号，这类宽带干扰的信号形式往往具有一定的参数化结构，并且在时域、频域与SAR有用信号高度混叠，很难直接通过时域或频域操作实现干扰抑制。

有效地识别和抑制WBI成为提高SAR图像质量一个关键技术。目前常见的宽带干扰抑制方法可分为参数化方法[1-10]和非参数化方法[11-14]两类。参数化方法是利用干扰信号的参数化结构，将宽带干扰信号用二阶或高阶多项式相位信号加以近似，并通过最小均方准则和最大似然准则估计参数化模型的相关参数，实现对干扰信号的重构和对消。但是，参数化方法依赖于模型结构的准确性，当模型结构存在误差时，会导致宽带干扰抑制效果的下降，同时参数化方法中的参数搜索和干扰数学建模等操作增加了算法的计算复杂度，造成算法实时性下降。另一种是非参数化方法，该类方法是利用谱估计的方法对干扰进行识别，然后在时域、频域或时频域上进行滤波处理，例如频率陷波法和时频滤波方法。频域陷波法是在受到干扰污染的SAR回波数据频谱中检测并识别干扰信号，然后将干扰所在的频带置零实现干扰抑制。虽然频率陷波法能有效抑制WBI，但是由于抑制干扰的同时损失了与干扰处于同一频带的有用信号，造成信噪比的降低。时频滤波方法采用基于时频分析的时变滤波技术，在有用信号与干扰信号时频支撑区近似可分的条件下，即可获得有用信号能量损失较小的宽带干扰抑制性能，但当有用信号与干扰信号的时频支撑区重合时，则同样会损失与干扰处同一频带的大部分有用信号。针对以上问题，本文提出了一种基于分数阶傅里叶变换(FrFT)的自适应信号分离的干扰抑制算法。由于蓄意干扰主要来源于其它雷达发射信号，且雷达发射信号大多数为线性调频信号(LFM)，而LFM在FrFT域具有良好的能量聚集性，因此结合干扰的参数化结构，采用FrFT变化使WBI在最佳变换域内变为NBI，而有用的回波信号在最佳变换域内类似于宽带的噪声信号，根据这一特性利用自适应信号分离算法将NBI与有用信号分离，从而实现WBI抑制目的。

1干扰信号模型

SAR系统很容易受到处于同一频段窄带信号和宽带信号的干扰，这些干扰的存在将会降低SAR图像的信干噪比，从而影响图像判读和增加后处理的难度存。存在干扰时的SAR回波数据可写成：

(1)

(2)

2FrFT自适应信号分离算法

自适应信号分离算法可在无独立期望信号的情况下实现宽带信号和窄带信号分离[15]。由于SAR发射的是线性调频信号，其接收到的回波信号具有宽带信号的特性。但对于WBI，由于有用信号和干扰信号均为宽带信号，若直接采用自适应信号分离算法无法实现干扰抑制的目的，因此需要先将WBI变为NBI。宽带干扰信号的带宽BWBI与有用信号的带宽Bs满足BWBI≤Bs，则宽带干扰信号经过FrFT后在某一分数阶变换域上可视为窄带信号，而有用信号经过FrFT后分散到整个变换域内，与NBI相比，具有类似噪声的随机统计特性。因此在最佳变换域内对回波信号进行自适应信号分离，则可以实现分离干扰和有用信号的目的。

2.1FrFT

FrFT可以解释为信号的时频分布在旋转后的分数阶域上的投影，若将傅里叶变换看成是在时频平面里由时间轴旋转π/2到频率轴，则FrFT可以看作是将信号在时间轴逆时针旋转α角到u轴。因此，以旋转角为变量进行扫描，在其中一个旋转角度上，LFM信号在分数阶域上能量聚集性达到最佳，如图1所示。

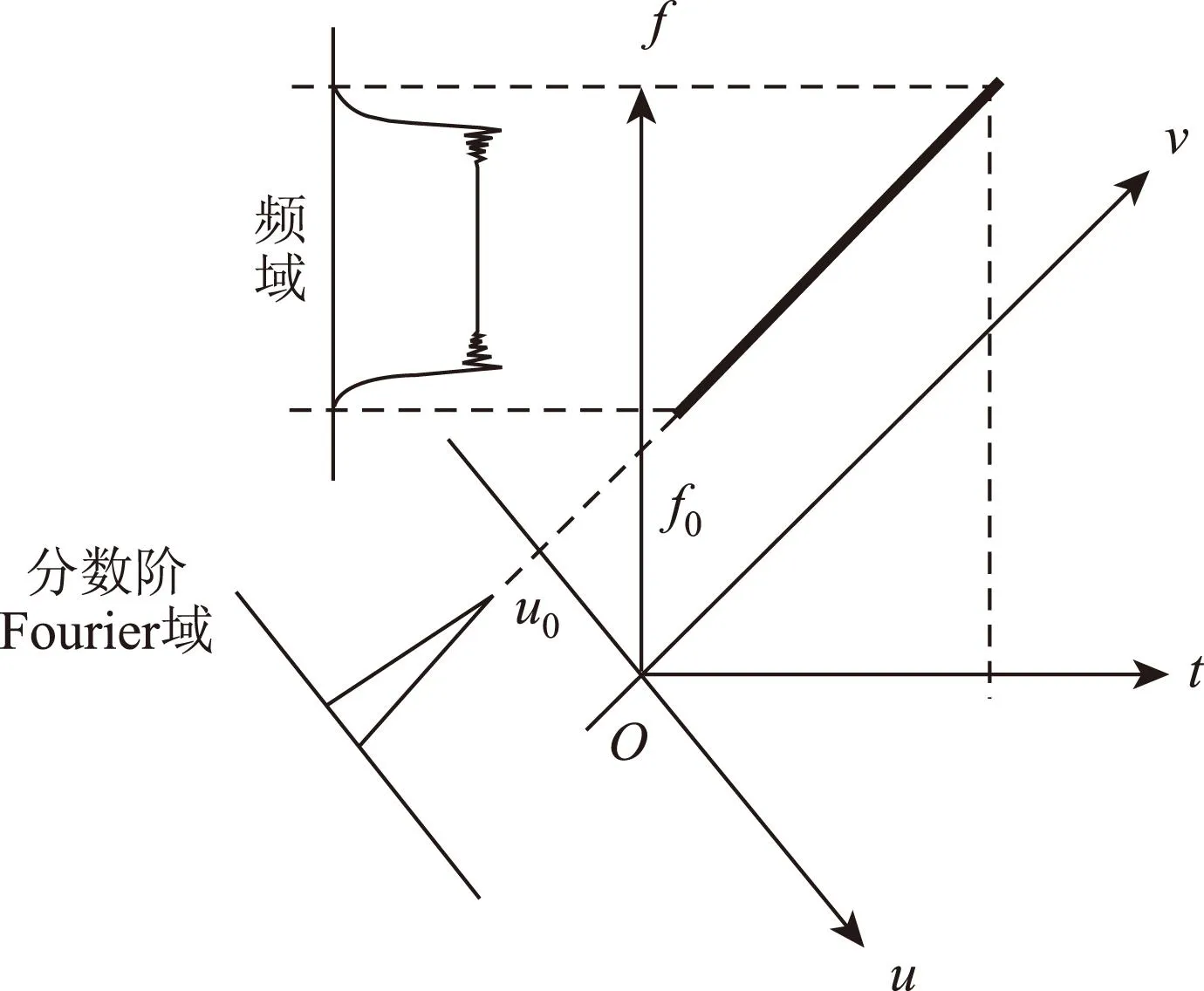
图1　FrFT示意图

信号x(t)的FRFT定义为[10]：

(3)

式中，Kp(t,u)为变换核

(4)

Fp为FRFT的算子；p∈(0,2]为FRFT的阶数，α=pπ/2为旋转角度。将式(2)代入式(4)中，并考虑只有一个干扰的情况，则可以得到WBI经FrFT变换后的表达式：

(5)

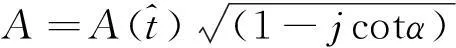
(6)

由上式可知，WBI在某一分数阶域上可视为窄带信号，对变换后的存在干扰的信号再进行自适应信号分离处理实现WBI干扰抑制。

2.2自适应信号分离

自适应信号分离是通过将窄带和宽带混合信号延时，由于延时后宽带信号与原来的输入不相关，而对于窄带信号延时前后仍保持较强的相关性，因此自适应信号分离算法能够自适应地与相关的窄带信号进行匹配，从而实现窄带信号和宽带信号分离。频域LMS算法[15]首先将宽带和窄带混合信号x(n)延时Δ构建期望信号d(n)，其中时延Δ应大于宽带信号的相关时间，然后将混合x(n)分割成长度为M的K块数据：

X(k)2M×2M=diag{FFT[x(kM-M),…,

(7)

则响应的滤波器输出可以表示为：

y(n)1×M=IFFT[W(k)X(k)]后M个元素

(8)

其中，y(n)只包含窄带信号，即NBI信号。误差信号e(n)中窄带信号被抵消而只保留宽带信号，即有用的SAR回波数据：

(9)

权值W每M点更新一次，而每次更新由M个误差信号e(n)累加控制，这样可保证与时域LMS具有相同的收敛速度。权值W迭代过程可表示为：

(10)

式中，μ为自适应步长；

(11)

(12)

其中，FFT{·}和IFFT{·}分别表示傅里叶变换和傅里叶逆变换；diag是将向量变成对角矩阵；上标T、H分别表示转置和共轭转置。

2.3FrFT自适应信号分离算法步骤

假设SAR回波数据x(n)包含有用的回波数据以及WBI，则干扰抑制过程如下：

Step1：采用FrFT估计出干扰信号的最优阶数p；

Step2：将回波数据x(n)变换到p-1的分数阶域上，在该变换域内具有线性调频特性的宽带干扰信号可视为窄带信号，而有用信号仍保持宽带信号的特性，即使当BWBI=Bs时，有用信号与NBI相比，类似于噪声信号(见仿真分析)；

Step3：在最佳变换域内采用自适应信号分离算法分离窄带干扰和宽带的有用信号；

Step4：将分离后的宽带信号做1-p阶的FrFT变换，此时得到的信号即为有用的SAR时域回波数据。

图2　FrFT自适应信号分离算法流程图

2.4变换阶数对FrFT自适应信号分离算法影响

根据式(5)，当变换阶数不等于-πarccotk/2时，WBI在变换域内不再满足窄带特性。这是因为不精确的变换阶数导致在式(5)中存在二次相位，这将导致LMS算法的信号分离性能。对式(6)求偏导得：

(13)

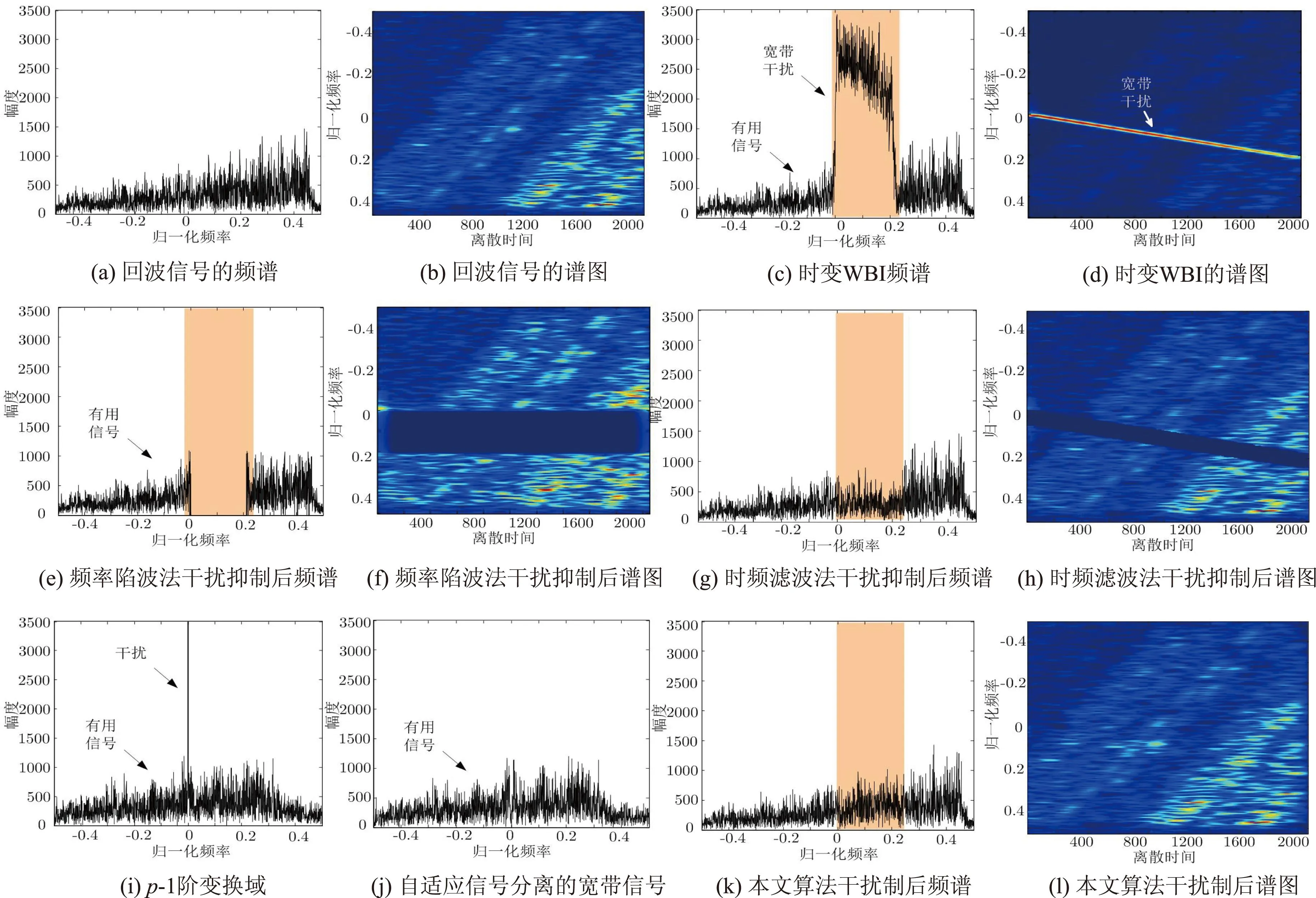
图3　WBI抑制算法比较

其中，Δp代表搜索步长，Δk代表调频率的分辨力。当p不变时，搜索步长越小，调频率分辨率越高。因此，为保证WBI在分数阶域满足窄带特性，则需要缩短搜索步长。为降低运算量，可以先采用步长0.01对干扰信号的阶数进行粗搜，确定大致的干扰信号阶数后，缩小阶数搜索范围，再采用步长0.001对阶数进行细搜，这样可以在保证阶数估计精度的同时大大降低运算量。

3计算机仿真与性能分析

3.1干扰抑制算法比较

在这一节中，通过在实测的SAR回波数据中加入模拟的干扰信号来验证算法的可行性，其中干扰信号带宽与有用信号带宽之比为0.15。图3(a)、(b)分别为SAR实测数据中某一个脉冲回波信号的频谱和时频谱图，由于信号包含来自不同方向、不同距离和不同散射点的回波信号，这些回波信号具有不同的相位和幅度响应函数，因此散射点回波在该频谱和时频谱图中具有明显的随机特性。在回波数据中加入一个时变WBI如图3(c)、(d)所示，由WBI的频谱可以看出，WBI占据有用信号的大部分频率单元，当采用频率陷波法对WBI所在区域进行干扰抑制时，会损失与WBI所处同一频段的大部分有用信号，造成严重的信号能量损失，如图3(e)、(f)所示；而由WBI的时频谱图可以看出，WBI在时频面内具有很强的时频聚集特性，并且WBI在每个离散时刻只占据了一小部分有用信号，在时频面内滤波能在一定程度上降低有用信号损失，如图3(g)、(h)所示，但以上两种方法均以损失有用信号为代价抑制干扰。图3(i)-(k)是采用FrFT自适应信号分离算法抑制WBI的结果。图3(i)是将回波数据x(n)变换到最佳的变换域内，在变换域内宽带信号变为窄带信号，而有用的回波信号与干扰信号相比类似于噪声信号，图3(j)是经自适应信号分离后宽带有用信号，图3(k)、(h)是对干扰抑制后有用的SAR回波数据频谱和时频谱图，与频率陷波和时频滤波方法相比，FrFT自适应信号分离算法在抑制WBI的同时也保留了大部分有用信号。

3.2干扰信号带宽和最佳变换阶数估计误差对干扰抑制的影响

为定量评估本文算法，引入信息熵作为干扰抑制后成像质量好坏的一个判决标准，熵值越低则成像质量越好；反之，亦然。图像g(m,n)的信息熵可定义为：

(14)

(15)

因此，文中采用干扰信号带宽的相对误差δ来描述最佳变换阶数的估计相对误差：

(16)

式中，Δ为干扰信号带宽的绝对误差，Be为估计的干扰信号带宽，Br为真实的干扰信号带宽。由图可以看出，当δ为1%时，误差对干扰抑制效果的影响比较小，当δ为4%和10%时，熵值会随干扰信号带宽的增加而逐渐增大，这是因为随着带宽的增大，干扰信号带宽估计的绝对误差也逐渐增大，从而导致WBI在该变换域内不再满足窄带特性。当BWBI/Bs>0.7后，误差为4%和10%的熵值分别与时频滤波法和频率陷波法的熵值相当。对式(13)左右两边求导，可以得到干扰信号带宽的分辨率表达式：

(17)

由上式可知，在阶数p和时宽一定的前提下，干扰信号带宽与阶数p的搜索步长有关，将ΔB代入到式(16)的Δ中可得到理论的干扰信号带宽估计的相对误差。图5分别给出了搜索步长为0.01和0.001在不同干扰带宽下的相对误差比较，由图可以看出，当搜索步长为0.01，BWBI/Bs<0.4时，相对带宽误差大于4%，而根据图4可知，在这区域内信息熵要远小于其它两种方法，而当BWBI/Bs>0.4时，相对带宽误差保持在4%左右，其干扰抑制性能与时频滤波法相当；而当搜索步长为0.001时，相对误差小于1%，其性能与不存在误差时的干扰抑制性能相当，但会增加算法运算量。为降低运算量，可以先采用步长0.01对干扰信号的阶数进行粗搜，确定大致的干扰信号阶数后，缩小阶数搜索范围，再采用步长0.001对阶数进行细搜，这样可以在保证阶数估计精度的同时大大降低运算量。

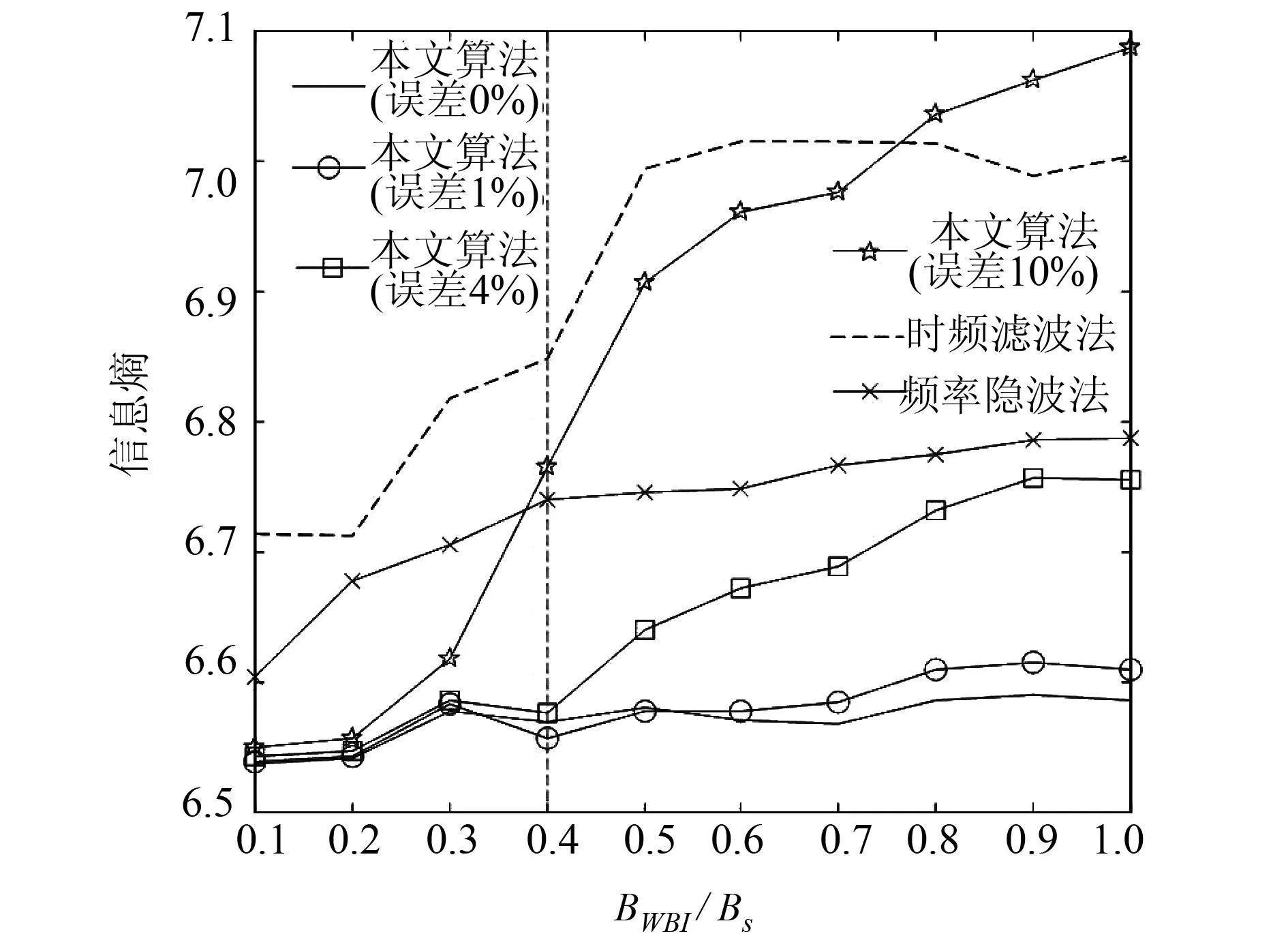
图4　三种算法熵值比较图

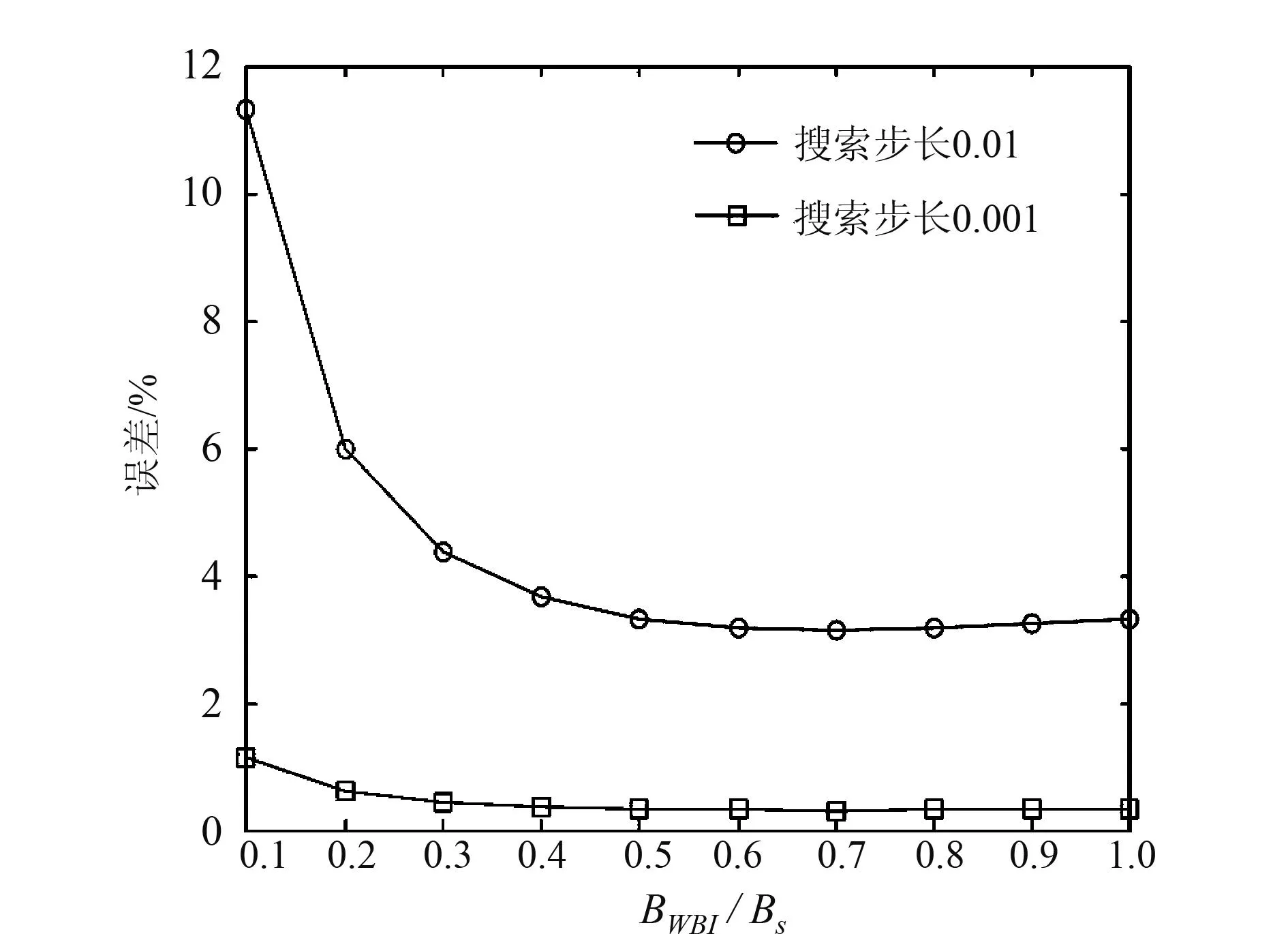
图5　搜索步长与估计相对无偿关系图

3.3SAR场景实测数据处理结果

在这一小节中所用的实测数据来源于加拿大航天局提供的加拿大温哥华地区的RADARSAT-1(精细模式2)。图6(a)给出了受WBI影响SAR回波数据直接成像结果，图中大部分场景被强的WBI覆盖，无法识别港口的轮廓和海上的舰船目标。图6(b)是采用频率陷波法干扰抑制结果，由于与WBI在频谱上重叠的大部分有用信号被陷波,信号损失严重， 图像WBI被消除的同时，也带来了噪声的增加，导致方框内舰船目标散焦，场景图像模糊。采用时频滤波干扰抑制算法能够得到清晰的场景轮廓和海上舰船目标，但与本文所提的干扰抑制结果相比，时频滤波方法干扰抑制后，方框内舰船目标仍存在一些散焦，两种方法的处理结果分别如图6(c)和6(d)所示。

表1给出了三种干扰抑制算法信息熵的结果，可以看出本文所提算法的熵值低于频率陷波法和STFT干扰抑制算法，因此基于FrFT自适应信号分离算法WBI抑制能力要优于其它两种方法。

图6　三种方法宽带干扰抑制后成像结果

WBI抑制方法陷波法时频滤波法本文方法图像熵14.248113.773513.4676

4结语

本文提出一种基于FrFT自适应宽带干扰抑制方法。该算法利用非蓄意干扰的参数化结构，采用FrFT将WBI变为NBI，再采用自适应信号分离算法在分数阶域内实现NBI与有用信号的分离，最终达到干扰抑制的目的。根据实测数据仿真分析可知，FrFT自适应信号分离算法在抑制WBI的同时也保留了大部分有用信号，根据仿真实验和实测数据分析可知，本文算法WBI抑制能力要优于频率陷波和时频滤波算法。

参考文献：

[1]Liu Z L, Liao G S, Yang Z W.Time Variant RFI Suppression for SAR Using Iterative Adaptive Approach. Geoscience and remote sensing letters, 2013, 10(6):1424-1428.

[2]Zhou F, Sun G, X Bai, Bao Z. A novel method for adaptive SAR barrage jamming suppression. Geoscience and RemoteSensing Letters, 2012,9(2):292-296.

[3]Miller T, Potter L, McCorkle J. RFI suppression for ultra wideband radar. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(4): 1142-1156.

[4]Ulug B. An algorithm for sinusoidal interference reduction using iterative maximum likelihood estimation techniques. Ohio State University, 1992.

[5]Smith T L , Hill R D , et al. Filtering approaches for interference suppression in low-frequency SAR. IEE Proc -Radar, Sonar & Navig, 2006, 153(4): 338-344.

[6]Zhou F, Wu R, Xing M, Bao Z. Eigen subspace-based filtering with application in narrow-band interference suppression for SAR. Geoscience and Remote Sensing Letters, 2007, 4(1): 75-79.

[7]Zhou F, Tao M, Bai X, et al. Narrow-band interference suppression for SAR based on independent component analysis. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(10): 4952-4960.

[8]Zhou F, Xing M, Bai X, Sun G, Bao Z. Narrow-band interference suppression for SAR based on complex empirical mode decomposition. Geoscience and Remote Sensing Letters, 2009, 6(3): 423-427.[9]Zhao Z, Shi X. FM interference suppression for PRC-CW radar based on adaptive STFT and time-varying filtering. Systems Engineering and Electronics. 2010,21(2): 219-223.

[10]Zhang S X, Xing M D, Guo R, et al. Interference suppression algorithm for SAR based on time-frequency transform. IEEE Transactions on Geoscience and Remote Sensing, 2011, 41(10): 3765-3779.

[11]Cui Y, Wang J. Wideband LFM Interference Suppression Based on Fractional Fourier Transform and Projection Techniques[J]. Circuits, Systems, and Signal Processing, 2014, 33(2): 613-627.

[12]Guan J, Chen X L, Huang Y, He Y. Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter. IET Radar Sonar Navig., 2012, 6(5): 389-401.

[13]Almeida L B. The fractional Fourier transform and time-frequency representations[J]. Signal Processing, IEEE Transactions on, 1994, 42(11): 3084-3091.

[14]Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Transactions on signal processing, 1996, 44(9): 2141-2150.

[15]Luo X, Ulander L M H, Askne J, Smith G. RFI suppression in ultra-windeband SAR systems using LMS filters in frequency domain. Electronics Letters, 2001, 37(4): 241-243.

FrFT Based Adaptive Interference Suppression Algorithm for Time-varying Wide-band Interference

LIU Bing-rui1，Su Jia2

(1.The 15thResearch Institute of China Electronics Technology Group Corporation, Beijing 100083, China；2.School of Electronics and Information, Northwestern Poly-technical University, Xi’an 710071 China)

Abstract:Wide-band interference (WBI) is common jamming signals against synthetic aperture radar (SAR), which can degrade the imaging quality severely. In this paper, an fractional Fourier transform (FrFT) based adaptive interference suppression algorithm is proposed, which is based on linear frequency modulation (LFM) property of WBI. In this algorithm, SAR echo data is transformed into the FrFT domain, and then the WBI becomes narrow-band interference (NBI) in the best transform domain. After that, NBI and useful SAR signal are separated using adaptive least-mean square (LMS) filters in the best transform domain. The proposed algorithm cannot only suppress the WBI, but also preserve the useful information as much as possible. The effectiveness of the proposed algorithm is demonstrated by the simulation data and measured data.

Key words:SAR; interference suppression; FrFT; adaptive signal separation

doi:10.3969/j.issn.1673-5692.2016.03.019

收稿日期：2016-05-01

修订日期：2016-06-12

基金项目：国家自然科学基金(61271416，61501376，61301093)

作者简介

刘秉瑞(1958—)，男，高级工程师，主要研究方向为信息系统、信号传输时延功率谱研究；

E-mail：liubr15@163.com

粟嘉(1985—)，男，博士，主要研究方向为雷达信号处理、时频分析。