二维向列型液晶的I-N相变及纹影织构模拟
杨胜林,朱福和,王 伟,杨 勇,王 芳,陈鹏飞
(1.东华大学纤维材料改性国家重点实验室,上海 201620;2.中国石化仪征化纤有限责任公司研究院,江苏仪征 211900;3.江苏省高性能纤维重点实验室,江苏仪征 211900;4.中国石化仪征化纤有限责任公司高纤中心,江苏仪征 211900)
研究论文
二维向列型液晶的I-N相变及纹影织构模拟
杨胜林1,朱福和2,3,王伟2,3,杨勇3,4,王芳3,4,陈鹏飞1
(1.东华大学纤维材料改性国家重点实验室,上海201620;2.中国石化仪征化纤有限责任公司研究院,江苏仪征211900;3.江苏省高性能纤维重点实验室,江苏仪征211900;4.中国石化仪征化纤有限责任公司高纤中心,江苏仪征211900)
摘要:从液晶的Landau-de Gennes自由能出发进行推导,发现在二维情况下向列型液晶的I-N相变为二级相变,且相变点为Nωφ2;在液晶畸变自由能单一Frank常数假设下,利用元胞动力学方法对二维向列型液晶的Ginzberg-Landau方程进行计算机模拟,得到了其纹影织构图样。
关键词:向列型液晶I-N相变纹影织构模拟
1966年,Du Pont公司首次用溶致性液晶聚合物聚对苯甲酰胺制备出高强、高模的商品纤维—Fiber B,随后又于1972年开发出著名的Kevlar纤维,它是由聚对苯二甲酰对苯二胺(PPTA)的硫酸溶液通过液晶纺丝工艺制备而成的。大量研究表明,Kevlar纤维的优异性能是与PPTA硫酸溶液的液晶性质密切相关的。
观察液晶性质,如其相变点(相变浓度、相变温度)和液晶织构,最简便和最有力的工具是热台偏光显微镜,此时,液晶样品往往是夹置于两片盖玻片之间的极薄的薄膜试样。从某种意义上讲,这些液晶薄膜可以认为处于二维状态。本文就二维情况下向列型液晶(制备高性能纤维的液晶高分子多属此类)的I-N相变进行了探讨,并模拟了其纹影织构。
1二维向列型液晶的I-N相变
我们讨论棒状分子在没有浓度涨落(φ为常数)时的I-N相变特征。在单轴取向的情况下取向张量S可表示为:
(1)
式中n为液晶取向矢,标量S表征取向程度,d为空间维度。
根据Landau-de Gennes理论[1-2],液晶的取向自由能密度为:
(2)
式中B、C和D是与液晶浓度以及分子量有关的系数,ω是液晶分子间的各向异性相互作用参数,与温度有关。由于三次方项的存在,I-N相变在d=3时是一个一级相变,因为S和-S代表着不同的取向状态,它们具有不同的能量。然而在d=2时,容易验证二维张量S满足tr(S·S·S)=0,这样相变就变成二级的了。此时尽管-S表示棒状分子沿着与S代表的方向垂直的方向排列,但由于分子总排列在一个平面内,它们仍然具有相同的能量。
将式(1)带入式(2),在d=2时得到:
(3)
取向度是方程∂f/∂S=0的解,亦即:
(4)
由上式容易解得S= 0以及:
(5)

(6)
可见,二维液晶的相变点为Nωφ = 2。当Nωφ< 2时,S= 0,此时体系是各向同性的;当Nωφ≥ 2时,体系处于取向有序的向列态,取向度取大小相同而符号相反的某一数值,所表示的取向方向相互垂直而与之对应的能量则相同。
2二维液晶相变的CDS模拟
在一个液晶体系中,存在许多“相畴”,在一个相畴内,液晶择优取向;而相畴之间,其择优取向方向并不相同。这些取向不同的相畴之间会形成所谓的畸变弹性进而对体系自由能产生贡献。液晶存在三种以及扭曲、展曲和弯曲畸变,可以用S的不同空间导数描述,其对自由能的贡献则对应着三个不同的弹性常数,称为Frank常数[2]。若采用单一Frank常数假设,二维液晶的自由能可表示为:
(7)
而描述S的时间演化的Ginzberg-Landau方程为:
(8)
式(7)、(8)中u、r、K和Γ。式(8)中的泛函导数为:

(9)
类似式(1),若将S表示为:
(10)
则有:
(11)
将式(10)、(11)代入式(9)得:
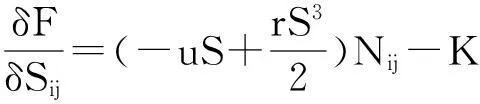
(12)
类比于标量的元胞动力学方法(CellDynamicScheme,CDS)[5-6]进行处理,可将上式写为:
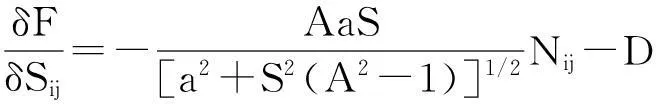

(13)
式中A、D为正的参数,A与淬冷度(液晶由清亮点骤冷到液晶态的程度)相关而D与液晶分子的旋转扩散能力相关。S的平衡值为:
(14)
在二维情况下,式(1)中的取向矢n成为平面单位向量,假设n与直角坐标XOY的x轴夹角为θ,于是S可写作:

(15)
作为验证,我们用这种方法模拟了液晶的相变并与实验结果进行对比,考察了液晶体系从清亮点上冷却到向列相态的某一温度,液晶体系从各向同性态转变为各向异性态的过程。
图1是芳纶纺丝液的偏光显微照片,它是将芳纶纺丝液涂敷到载玻片上,在热台上加热至溶液变透明再冷却到室温,然后在偏光显微镜下进行观察拍照得到的。

图1PPTA/H2SO4液晶溶液的POM照片
芳纶纺丝液是PPTA/H2SO4溶致性向列型液晶溶液,在偏光系统下呈现亮场并可以观察到丝状黑色条纹汇聚到一点的情形,这就是所谓的向列相液晶的纹影织构。
而根据式(8)、(13),可以用数值方法求解S的时间演化过程,并用图示模拟纹影织构的形成。首先,在128×128的格子上,令式(15)中的Sxy、Sxx为0±0.001区间内均匀分布的随机数作为S的初始条件(表示起始状态是各向同性态);然后在式(13)中取A=1.5,D=0.5,a=0.5,用CDS进行数值模拟,可以得到S(即Sxy、Sxx)随时间变化的数值。
现假设偏光显微镜的起偏器和检偏器的方向为x、y(为相互垂直的两个单位向量),由光源而来的入射光经过起偏器后的电场为E0x,若液晶的极化率张量为α,光线通过液晶后电场变为α·E0x,若再经过检偏器,则出射光的电场变为α·E0x·y。液晶的极化率张量α正比取向张量S[2,7],于是出射光的光强I为:
(16)

图2 用CDS方法模拟得到的液晶纹影织构(图中灰度代表S2xy的大小,图下数值代表模拟时间步长)
3结果与讨论
其实已有理论计算和实验表明,液晶的Landau-de Gennes自由能中的三次方项系数C很小,液晶的I-N相变是一个弱的一级相变,在二维情况下则直接成为二级相变,其相变点为Nωφ= 2。可以看出,当液晶的分子量N越大、浓度φ越高时,越容易处于向列态;而ω作为液晶分子间的各向异性相互作用参数,类似于Flory-Huggins参数,一般与温度成反比,故温度升高会使液晶变回各向同性态,此即液晶“清亮点”的出现,这些与通常的实验结果都是一致的。因此,在用热台偏光显微镜观测液晶薄膜时,可以安全地把对象视为二维。此外,用二维情况来处理液晶,在利用Landau-Ginzberg方程探讨液晶I-N相变时,可以利用CDS方法大大简化计算,得到可以与实验观察对照的模拟结果(如纹影织构),这有利于我们从实验和理论两方面对高分子液晶的性质进行深入研究,为基于液晶高分子的高性能纤维等材料的制备奠定基础。
参考文献:
[1]Chandrasekhar S. Liquid Crystals [M]. Cambridge University Press, London, 1992: 61-62.
[2]Gennes P G. The Physics of Liquid Crystals [M]. Clarendon Press, Oxford, London, 1974: 41-92.
[3]Liu A J, Fredrickson G H. Free energy functionals for liquid crystalline polymer solutions and blends [J]. Macromolecules. 1993, 26: 2817-2824.
[4]Fukuda J.Free energy of semiflexible polymers and structure of interfaces [J]. The European Physical Journal B. 1999, 7: 573-583.
[5]Oono Y, Puri S. Study of phase-separation dynamics by use of cell dynamical systems I. Modeling [J]. Physical Review A. 1988, 38: 434-453.
[6]Oono Y, Puri S. Study of phase-separation dynamics by use of cell dynamical systems II. Two-dimensional demonstrations [J]. Physical Review A. 1988, 38: 1542-1565.
[7]Yang S L, Liang B R. Simulation ofphase-separated structures of liquid crystalline polymer /flexible polymer blends [J]. Journal of Polymer Science: Part B: Polymer Physics. 2001, 39: 2915-2921.
I-N phase transition and schlieren texture simulation of 2D nematic liquid crystal
(Yang Shenglin1, Zhu Fuhe2,3, Wang Wei2,3, Yang Yong3,4, Wang Fang3,4, Chen Pengfei1)
(1.StateKeyLaboratoryforModificationofChemicalFibersandPolymerMaterials,DonghuaUniversity,Shanghai201620,China;2.ResearchInstituteofSinopecYizhengChemicalFibreL.L.C.,YizhengJiangsu211900,China;3.JiangsuKeyLaboratoryofHighPerformanceFiber,YizhengJiangsu211900,China;4.HighPerformanceFiberProductionCenterofSinopecYizhengChemicalFiberL.L.C.,YizhengJiangsu211900,China)
Abstract:The isotropic-nematic (I-N) phase transition of nematic liquid crystal has been found to be a second-order one in two-dimensional case and the transformation point should be Nωφ = 2, which could be directly derived from the Landau-de Gennes free energy about the liquid crystal. Under the assumption of single Frank constant of distortion energy for the liquid crystal, the simulated schlieren texture has also be obtaind by numerically solving the Ginzberg-Landau equation of liquid crystal with cell dynamic scheme.
Key words:nematic liquid crystal; isotropic-nematic phase transition; schlieren texture; simulation
收稿日期:2016-05-20
作者简介:杨胜林(1973-),湖北云梦人,工学博士,主要从事基于高分子液晶的高性能纤维及其复合材料等方面的研究。
中图分类号:O631.1
文献标识码:A
文章编号:1006-334X(2016)02-0001-03

