我国商业银行利率不确定性实证研究

刘澄，皇甫玉婷，赵若

（北京科技大学东凌经济管理学院，北京　100083）



我国商业银行利率不确定性实证研究

刘澄，皇甫玉婷，赵若

（北京科技大学东凌经济管理学院，北京100083）

［摘要］通过运用GARCH-VaR模型对银行利率的风险进行度量，选取1年期上海银行间同业拆借的隔夜利率数据（Shibor）进行实证分析。结果显示Shibor对数收益率的统计分布为非正态分布且为时间稳定序列，同时存在一定自相关性及异方差性。随后采用AR（1）-GARCH（1，1）模型在三个不同的残差分布假设下，对数据进行模拟并计算VaR值，并采用失败检验法对VaR值进行回测检验，结果表明在GARCH-VaR模型下，当假设残差分布为正态分布和广义误差分布时，计算得到的VaR值更合理，能够通过回测检验；而残差分布为学生t分布时，风险值会被高估，无法通过回测检验。

［关键词］利率市场化；利率风险；VaR模型；自回归条件异方差

1　引言

我国利率市场化转变主要依托“政府渐进”模式实施［1］。到目前为止，除存款利率尚未完全放开外，我国利率市场化已逐步实施［2］。利率市场化会对我国商业银行的传统经营模式造成冲击，存贷利差在利率完全市场化后短期内将会明显收窄［3］。商业银行不得不在平衡收益与风险的基础上合理定价，即在获得市场份额的同时又能以合理定价有效覆盖风险［4］。

随着我国利率市场化进程的逐步深入，我国商业银行利率的不确定性和波动性也逐步增加，利率风险成为我国商业银行所面临的主要风险之一［5］。如何有效的识别、衡量及管理利率风险已成为我国商业银行面临的重要挑战［6］。利率风险的度量是利率风险管理的前提［1］。西方发达国家有较为成熟的利率风险度量模型值得借鉴和参考［7］：利率敏感性缺口模型［8］、久期分析［9］、VaR方法及模拟法［10］。由于VaR方法的简洁性、市场风险的可防范性等优势，被广泛采纳［11］。由于我国银行利率长期以来处于管制状态，在银行利率风险度量模型方面较为欠缺，国内关于VaR模型的研究起步也比较晚［12］。郑文通于《金融风险管理的VaR方法及其应用》［13］一文中就VaR模型引入我国的必要性进行了概况性的阐述，对VaR方法在我国风险度量方面的应用起到了一定的指导作用。李成、马国校应用VaR模型对我国银行间同业拆借市场每日加权平均利率进行实证研究［14］。

本文将选取2010年5月4日至2014年5月4日上海银行间同业拆借的隔夜利率数据（Shibor）共1 000个样本数据进行实证分析。对数据进行正态性检验、稳定性检验、自相关性检验以及条件异方差检验。结果显示，利率时间序列不满足同方差性，不能简单应用VaR模型进行计算，本文的模型建立将结合GARCH模型和VaR模型。考虑到利率时间序列的异方差性和自回归性，在三种不同分布（正态分布、学生t分布、广义误差分布）的假设条件下，分别建立AR（1）-GARCH（1，1）-N模型、AR（1）-GARCH（1，1）-t模型以及AR（1）-GARCH（1，1）-GFD模型，对Shibor数据进行模拟分析，并在对应模型下计算出相应的风险价值。为评定风险值的准确性，本文采用Kupiec提出的失败检验法对模型估计结果进行回测检验。检验结果显示，当假设残差分布为正态分布和GFD分布时，计算得到的VaR值更合理，能够通过回测检验；而残差分布为学生t分布时，风险值会被高估，无法通过回测检验。

2　模型

2.1VaR模型

VaR方法以数理统计为基础对风险进行衡量，用一个指标数值（VaR值）对风险状况进行表征。通过对置信度的设定，得到在不同的置信水平下的VaR值，对金融机构的风险进行不同程度的衡量。

在正态分布情况下的VaR值表达式如下：

其中W0为初始投资的资产金额，α为临界值，为在该期限内的回报率均方差。然而实际分布和正态分布相比，会出现“厚尾”和“峰位左偏”的现象，表明极端事件发生的概率要比标准正态分布中计算的概率要高一些。在这种情况下，可以假设该资产未来价值或者回报率的分布服从自由度为n的t分布。可以将计算VaR值的公式一般化为：

其中K（c）表示在特定分布和一定的置信区间C之下的临界值α。δ表示各种资产组合价值的标准差。如果只考虑线性风险因素，会有一定的局限性。鉴于此，引入非线性敏感程度以及其他风险因素，计算公式如下：

公式（3）中用di、dj分别表示资产组合价值对风险因素i、风险因素j变化的敏感性，ρij表示风险因素i和风险因素j之间的相关系数，δ1，δ2分别表示风险因素i、j的标准差，γi，γj分别为资产组合针对第i、j中风险因素的变化的非线性敏感程度，S2表示其他风险因素。

2.2自回归异方差模型

对于许多经济问题而言，μt的条件方差σ2往往依赖于很多时刻之前的变化量。如果考虑到σ2的计算式是σ2的一个分布滞后模型，用一个或者两个σ2的滞后值来代替较多的的滞后值，就得到了广义自回归条件异方差模型GARCH模型。

在GARCH模型（GeneraIized Autoregressive ConditionaI Heteroscedasticity modeI）中，需要考虑条件均值和条件方差两个不同的设定。

在金融领域中，对于含有多个ARCH项和GARCH项的高阶GARCH（q，p）模型，其条件方差表示如下：

其中q为GARCH的阶数，p为ARCH项的阶数；α（L）和β（L）是滞后算子多项式。

在实际中，很多金融时间序列的无条件分布较正态分布有更加“宽厚”的尾部，为了描述该分布的尾部特征，一般对误差项的分布情况做一定的假设。通常情况下，GARCH模型中关于残差分布的假设有以下三个：正态分布假设（亦成为高斯分布假设）、学生t分布假设以及广义误差分布假设（GFD假设）。

这里θ代表参数向量。

其中k为自由度，当k→∞时，学生t分布也趋近于正态分布。这样，参数的估计就变为在自由度k＞2的约束下使最大似然函数最大化的问题。

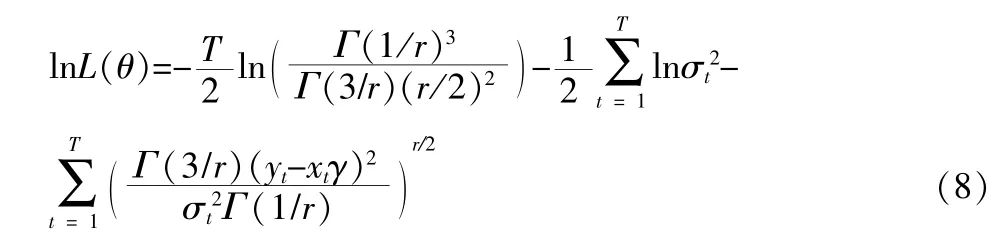
这里的r＞0，当r=2时，GFD分布就是一个正态分布。

本文将选用由FngIe于1982年提出的ATCH-LM检验模型来验证是否具有ARCH效应，即检验残差序列是否存在ARCH效应的拉格朗日乘数检验（Lagrange MuItipIier test）。

3　Shibor数据选取、统计特征及实证分析

3.1数据选取

我国商业银行利率市场化进程正逐步展开，由于中国银行同业拆借利率（China Inter-bank Offered Rate，Chibor）是由银行间融资交易的实际交易利率计算得出，加之银行间融资活动的不积极，使得Chibor数据不能很好地代表我国利率市场的实际情况。因此，选择市场化程度更高，稳定性和连续性都相对较好，并且能够提供一个较为统一、完整、有效的短期利率曲线的上海银行间同业拆借利率Shibor数据作为研究对象，对我国市场利率风险进行度量。

若按照时间周期分类，Shibor可以分为O/N（隔夜）、1 W（1个星期）、1 M（1个月）等种类。由于隔夜拆借利率的频繁度远大于其他周期的拆借利率，能够更好的反映市场状况，因此本文选取上海银行间同业拆借的隔夜利率数据进行实证分析。数据选取区间为2010年5月4日至2014年5月4日的Shibor数据，样本容量为1 000个。

3.2统计特征分析及回测检验

本文将对上海银行同业拆借隔夜利率做取对数处理：

Rt=In（Shibort）-In（Shibort-1）（9）

描述性统计分析如下：

如图1所示，上海银行同业隔夜拆解利率的对数收益中，偏度为0.514 144大于零说明隔夜拆解利率为右偏序列；峰度值大于3，说明样本序列的尖峰特点，由此可知样本数据不服从正态分布。分析可知Shibor对数收益率序列以0％为中心，在其附近上下波动，可初步判断相应的样本数据为随机序列。

本文选用ADF检验法对样本数据的平稳性进行检验。结合上述收益率走势曲线的特点可知Shibor对数收益率在零上下波动，没有明显趋势项。因此在单位根检验中不包含常数项和时间趋势项。如表1所示。

图1　Shibor对数收益率分布统计图

图2　Shibor的收益率走势曲线

表1　单位根检验

单位根检验结果显示，将ADF值与显著水平分别为1％、5％、10％的情况下所得检验值进行对比，不难发现ADF检验结果最小（绝对值最大），因此Shibor对数收益率为平稳的时间序列。

接下来检验数据的自相关性，数据处理如表2所示。

表2　自相关性检验

根据表2所得结果显示，各阶偏相关系数（PAC）和自相关系数（AC）均不为零，且在一阶滞后的情况下，P=0.003，即在95％的置信水平下拒绝原假设，序列存在自相关性。因此需要通过最小二乘法用AR（1）模型估计方程以消除自相关性。对Shibor收益率在LSM-AR（1）模型下进行模拟结果如表3所示。

表3　LSM-AR（1）模拟

在LSM-AR（1）模型下对收益率的残差序列进行一阶滞后的LM相关性检验如表4所示。

表4　残差序列进行一阶滞后的LM相关性检验

分析上表4可知在5％的显著水平下，在LSM-AR（1）模型下的残差序列不存在序列相关性，见表5。

表5　时间序列的ARCH-LM检验

分析得到的ARCH-LM检验结果：F统计量和T*R2统计量是显著的，其对应的P值均为零。因此，残差序列存在ARCH效应。

本文选取AR（1）-GARCH（1，1）模型对收益率序列进行分析，在正态分布、学生t分布以及GFD分布这三种残差分布假设上，结合GARCH模型来分析银行间同业拆借利率序列的风险值，并对三种不同分布下的结果进行分析。

在AR（1）-GARCH（1，1）-N分布模型中的均值方程和条件方差为：

在AR（1）-GARCH（1，1）-t 分布模型中的均值方程和条件方差为：

在AR（1）-GARCH（1，1）-GFD 分布模型下的均值方程和条件方差为：

对以上三个模型分别进行参数估计，计算得到标准差，在9 5％置信条件下得到分位数并最终求得每日的VaR序列见表6。

对于VaR值是否准确需要进行回测检验。本文将采用Kupiec提出的失败检验法对上述三种分布模型的VaR值进行检验。

假设（1-c）为置信水平，T为总的考察天数，N为考察期期间的失败天数，则失败频率为P=（N/T）。在零假设P=c的零假设条件下，构造服从自由度为1的卡方分布的似然比检验，来对失败频率与显著性水平c的差别进行评定。

Kupiec提出的似然比检验公式表示如下：

表6　AR（1）-GARCH（1，1）模型下的估计结果

将收益率按照大小排序，与三种不同分布模型下得到的VaR值相比，得到各个分布模型下的实际失败天数；同时，在置信水平为95％的条件下，确定相应的实际失败天数及实际失败频率，并计算出对应的LR统计量。结果如表7所示。

表7　三种不同分布模型回测检验表

根据表7得到的结论分析可知，用AR（1）-GARCH-N分布模型和AR（1）-GARCH-GFD分布模型估计的VaR值通过了回测检验，AR（1）-GARCH-t分布模型得到的VaR值未通过回测检验。AR（1）-GARCH-N分布模型和AR（1）-GARCH-GFD分布模型估计的VaR值非常接近，回测失败天数相同，均落在非拒绝域内，能够在一定程度上表示Shibor对数收益率的风险价值。

3　结论

本文运用GARCH-VaR模型对银行利率的风险进行度量，通过对上海银行间同业拆借利率数据建模进行实证分析，得出以下结论：①该数据序列是平稳的时间序列，存在“尖峰厚尾”现象，为非正态分布，并存在一定的自相关性和条件异方差性。②在残差序列的三种不同分布（正态分布、学生t分布、广义误差分布）的假设下建立模型对Shibor数据进行模拟分析及风险值VaR计算，通过Kupiec的失败频率检验法对计算结果进行衡量对比，结果显示AR（1）-GARCH-N分布模型和AR（1）-GARCH-GFD分布模型估计的VaR值非常接近，回测失败天数相同，均落在非拒绝域内，能够在一定程度上表示Shibor对数收益率的风险价值。而残差分布为学生t分布时则无法通过回测检验。③数据模型的选取对最终计算得到VaR值是否有效有较大影响。因此如何建立合理的数据模型对数据进行拟合，是进行风险计量的关键问题之一。

主要参考文献

［1］胡新智，袁江.渐进式改革：中国利率市场化的理性选择——利率市场化的国际经验及其对中国的启示［J］.国际经济评论，2011（6）.

［2］周小川.关于推进利率市场化改革的若干思考［J］.中国总会计师，2011（1）.

［3］周茂清.利率市场化给商业银行带来的机遇、挑战及其应对［J］.当代经济管理，2012，34（6）.

［4］武剑.利率市场化进程中的利率风险管理［J］.财经科学，2003（2）.

［5］贺国生，栗红宇.商业银行利率风险度量的历史演变及现实启示［J］.金融理论与实践，2005（1）.

［6］赵自兵.升息周期中商业银行的利率风险分析［J］.国际金融研究，2004（9）.

［7］L Angbazo.CommerciaI Bank Net Interest Margins，DefauIt Risk，Interest -Rate Risk，and Off -baIance Sheet Banking［J］.JournaI of Banking & Finance，1997，21（1）：55-87.

［8］Chen R，Yu L.A NoveI NonIinear VaIue-at -risk Method for ModeIing Risk of Option PortfoIio with MuItivariate Mixture of NormaI Distributions ［J］.Fconomic ModeIing，2013，35（9）：796-804.

［9］陈祖功，查奇芬.久期模型在银行利率风险测定中的应用［J］.统计与决策，2008（17）.

［10］Herrera R，Schipp B.VaIue at Risk Forecasts by Fxtreme VaIue ModeIs in a ConditionaI Duration Framework［J］.JournaI of FmpiricaI Finance，2013，23（5）：33-47.

［11］刘宇飞.VaR模型及其在金融监管中的应用［J］.经济科学，1999（1）.

［12］李焰.我国商业银行的利率风险及管理研究［J］.财贸经济，2000（9）.

［13］郑文通.金融风险管理的VaR方法及其应用［J］.国际金融研究，1997（9）.

［14］李成，马国校.VaR模型在我国银行同业拆借市场中的应用研究［J］.金融研究，2007（5）.

doi:10.3969/j.issn.1673 - 0194.2016.03.079

［中图分类号］F830.33

［文献标识码］A

［文章编号］1673-0194（2016）03-0144-05

［收稿日期］2015-12-01

［作者简介］刘澄（1967-），男，北京科技大学东凌经济管理学院金融系主任，教授，博士生导师，主要研究方向：信用管理，风险管理，投资规划与投资策略，金融营销，投资行为分析，金融机构管理，宏观金融政策。