不同密实度下黏性土的渗透性分析

陈宗先，何　翔，熊云山，王　锐

(武汉轻工大学 土木工程与建筑学院，湖北 武汉 430023)



不同密实度下黏性土的渗透性分析

陈宗先，何翔，熊云山，王锐

(武汉轻工大学 土木工程与建筑学院，湖北 武汉 430023)

摘要：土体是具有复杂物理性能的材料，土体的微观孔隙特征决定了土体宏观的渗透性，从而决定了土体的物理性质。对土体渗透性能与孔隙特征进行分析，采用变水头渗透试验。取武汉某工地的黏土来制备土体试样，测量其物理指标，进行风干过筛，采用静压试验制备重塑试样，用于渗透试验。分析结果表明：随着黏性土孔隙比e逐渐增大即土的干密度ρd逐渐减小，则渗透系数k也逐渐增大，并研究对比了渗透系数与孔隙比之间的多种经验关系。

关键词：渗透系数；孔隙比；渗透试验；重塑试样

1引言

土是一种松软堆积物，内部空间孔隙相互连通，土中水能透过土体发生渗流，土的渗透性是一个较复杂的研究课题，不少学者对其进行了研究，目前主要采用渗透试验和固结反演等方法确定土的渗透系数。对同一土样，渗透系数与固结压力或者孔隙比相关关系已有很多讨论[1]。孔隙比是表征土体孔径分布的宏观指标，是土体的应力状态、屈服状态、扰动状态等的最终反映，因此对渗透系数与孔隙比关系进行探讨并取得了相对统一的结论，分析有条件下饱和黏性土渗透特性的变化规律[2]。

为了研究黏性土的渗透性，进一步明确渗透系数与孔隙比相关关系，笔者对黏性土进行渗透试验。所进行的变水头渗透试验步骤为：(1)取自基坑底部的土体，测量土体物理性质指标并风干过筛，试验前制备了黏性土的重塑试样1组共5个。(2)将制备的重塑试样进行变水头渗透试验，对其结果进行渗透性数据分析，分析并探索渗透系数与其孔隙比的变化规律，研究试样的渗透性。

2试验材料与方法

2.1试验材料

试样取自武汉某工地深度为9 m基坑坑底处，将采集的土样进行风干，过2 mm的筛子筛选，测量其物理性质指标和物理特性。测得的土体含水率为ω0，经过计算称量一定量的土体与蒸馏水，按《土工试验技术手册》要求，制备含水率为15%的重塑土，将其密封静置24 h，复测含水率，最后含水率确定为15.13%[3]。

将试样制备成密度ρd分别为1.35 g/cm3,1.4 g/cm3,1.45 g/cm3,1.5 g/cm3,1.6 g/cm3五个等级，经计算之后再称取一定量的试样，制成1组5个平行试样,含水率确定为15.13%，用于渗透性试验。黏性土试样物理性质指标如表1所示。

表1试样土体的物理性质指标

埋深/m天然密度/(g/cm3)相对密度天然含水率/%液限/%塑限/%塑性指数92.032.7521.938.9520.4318.52

2.2试验方法

2.2.1试验原理

温度效应对黏性土的力学性能有一定影响，对于不同温度下的渗透试验，在一定温度范围内随着温度升高，土样渗透性呈线性增长；温度变化对黏性土液塑限和黏性土吸附结合水量都有影响[4]。因此，为了更好地进行变水头渗透试验，本试验的水温应控制在一定范围之内。本次渗透试验，试验水温经测定维持在7—9 ℃之间。

渗透系数k是反映土的渗透性强弱的指标，是渗流计算的重要参数，试验采用变水头法量测黏性土的渗透系数，水头在试验过程中是动态变化的[5]。运用渗透仪进行不同干密度下饱和黏性土的渗透分析，推出不同干密度下试样土体的渗透系数。试验装置如图1所示。

图1　试验装置

由图1可知，取细玻璃管的内截面截面积为a，试验试样的截面面积为A，试验过程中某一时刻t所对应的水头为h，时间间隔dt的水位差为dh，则在t至t+dt的时间，流经细管土样的水量dQ：

dQ=-adh.

(1)

式1中的负号代表渗流过程中水量随水位h的变小而增大。

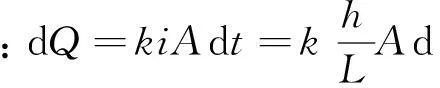
(2)

同一时间内，经过同一截面积的总水量相等：

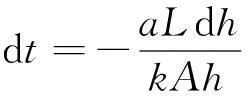
(3)

式3两边积分，积分后可得到：

(4)

即可得到土的渗透系数

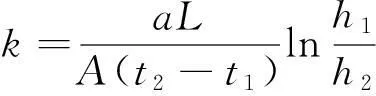
(5)

改为常对数表示，则可写成：

(6)

已知a、L、A，量测特定时刻t1,t2对应水位h1,h2即可求得渗透系数[6]。

制样时进行三次分层填土，使用液压千斤顶，用静压试验法。取一定质量试样(含水率测得为15.13%)制备五组平行试样，将制备的试样抽真空饱和，抽气持续4 h，放水中24 h，饱和度到95%后取出。

土的物理性质指标已知，则黏性土试样孔隙比e：

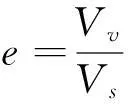
(7)

换算式：

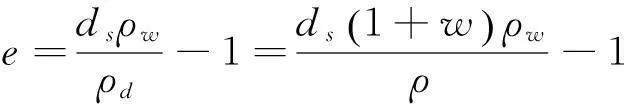
(8)

式中，土粒相对密度ds；ρ为土的天然密度，g/cm3；ρw为水的密度，g/cm3；ρd为土的干密度，g/cm3；e0为初始孔隙比。

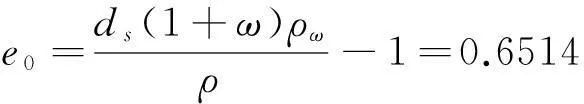
(9)

而重塑试样土体的干密度ρd分别为1.35 g/cm3，1.40 g/cm3，1.45 g/cm3，1.50 g/cm3，1.60 g/cm3，试样土体的孔隙率n：

(10)

求得的5组试样的孔隙比和孔隙率如表2所示。

表2土体试样编号及其物理指标

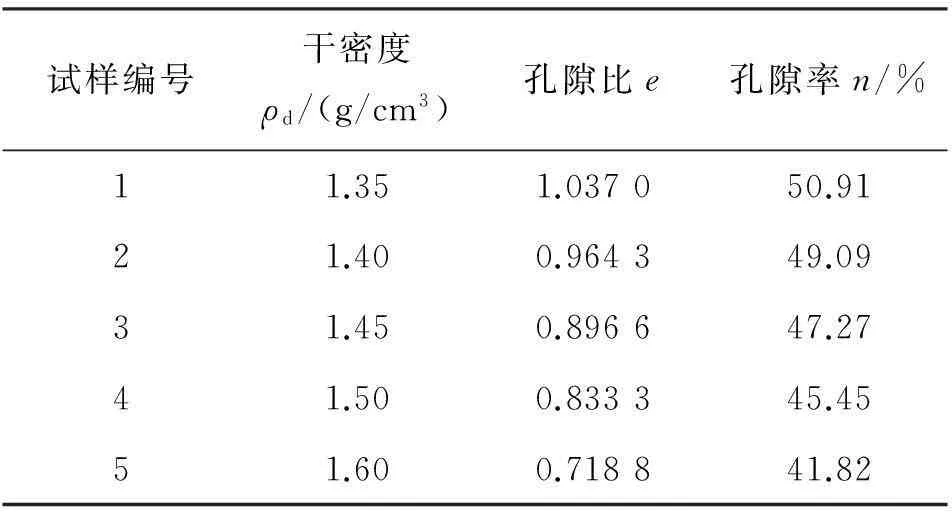
试样编号干密度ρd/(g/cm3)孔隙比e孔隙率n/%11.351.037050.9121.400.964349.0931.450.896647.2741.500.833345.4551.600.718841.82

本试验使用的五组试样，其变水管的截面积经测量分别是： 0.526 cm2,0.491 cm2,0.497 cm2,0.503 cm2,0.517 cm2。

2.2.2实验操作步骤

(1)切取试样。切取试样应尽量获取原状土。使黏土试样的上下面整平击实，在环刀内壁涂一层凡士林，慢慢地垂直下压 ，保持环刀和试样紧密贴合。

应用唑来膦酸后出现急性葡萄膜炎一般需要糖皮质激素治疗。本研究中1例患者首选给予眼部抗病毒及抗炎治疗，眼部症状恶化[16]，提示抗病毒及抗炎治疗通常无效。一般局部应用类固醇激素能使大部分病例的眼部症状完全缓解。如局部应用类固醇激素，患者眼部症状未明显改善，或患者急性葡萄膜炎始发症状较严重，可口服或静脉全身给予糖皮质激素治疗。另外，为解除睫状肌痉挛，改善局部血循环，减少渗出物，防止虹膜后黏连，可联合使用睫状肌麻痹滴眼剂[31]。

(2)使试样与刀刃相接的黏性土试样直径大于环刀的内径，将环刀放进渗透容器前涂层凡士林在容器内壁，装止水垫圈以及将螺母旋紧，将装有试样容器的供、进水的装置连通。关闭止水夹，直到水从排气孔流出，倒放容器，打开排气管管夹，再打开止水夹与进水夹，空气会排出，直到没有气泡排除为止。

(3)往变水头管中注水，等到了预期的高度后，把进水管夹打开，起始时间t1和终止时间t2，所对应的起始水头h1和终止水头h2,记录出口的开始和终止水温。

3试验结果与讨论

根据上述试验基本原理、操作步骤，并结合本节将要介绍的计算公式和温度校正系数，得到饱和黏性土的渗透系数k。

(1)T℃的渗透系数公式：

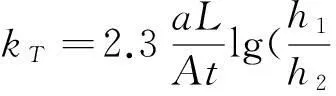
(11)

其中，a为测压管截面积；L为试样高度，即为渗径；h1为开始水头；h2为终止水头。

(2)水温20 ℃时的渗透系数：

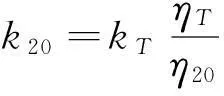
(12)

其中，kT、k20分别为T℃、20 ℃水温时的渗透系数(cm/s)；ηT、η20分别为T℃、20 ℃的动力黏滞系数(10-6kPa·s)。

渗透系数k与水的重度γω及黏滞度η有关，不同水温时，γω相差不多，η变化比较大。水温越高，η越低，k与η呈线性关系。温度T下测得的kT值应加温度修正，成为标准温度下渗透系数值。

确定能使度量正确、测量仪器和校正仪器都具有正确指示的温度。所以，水温因素的影响不容忽视。在本试验中，特别需要注意的是水头差应大于10 cm。针对本次渗透试验，试验水温经测定维持在7—9 ℃之间。规范中规定采用10 ℃或20 ℃水温的渗透系数为试验中标准渗透系数[7]。渗透试验中水的渗透力作用会使试样的干密度产生变化，会致使最后的结果误差变大。水的动力黏滞系数η、黏滞系数比ηT/η20、温度校正值Tp如表3所示。

表3水的动力黏滞系数η、黏滞系数比ηT/η20、温度校正值Tp

求得的5个黏性土试样的渗透系数如表4所示。

由现有数据绘制孔隙比e以及黏土试样干密度ρd分别与渗透系数k的关系图，如图2和图3所示。

表4黏性土试样的渗透系数

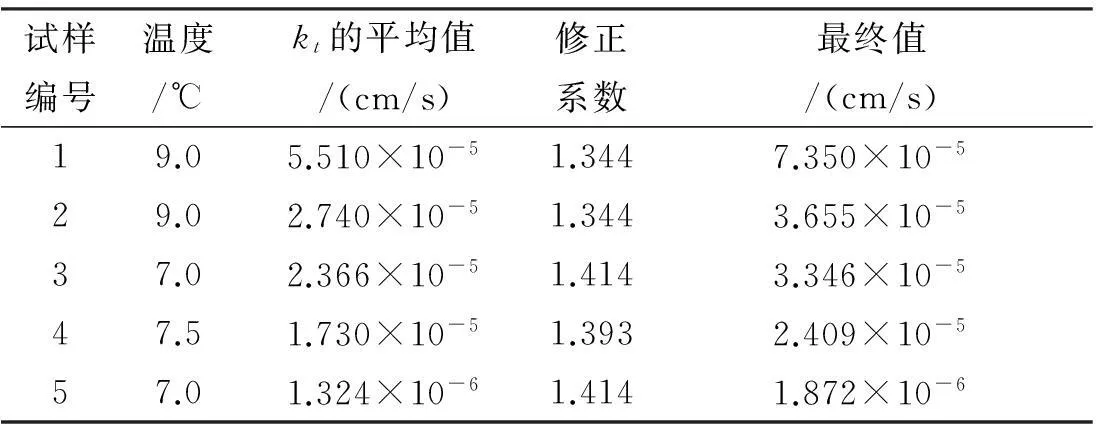
试样编号温度/℃kt的平均值/(cm/s)修正系数最终值/(cm/s)19.05.510×10-51.3447.350×10-529.02.740×10-51.3443.655×10-537.02.366×10-51.4143.346×10-547.51.730×10-51.3932.409×10-557.01.324×10-61.4141.872×10-6

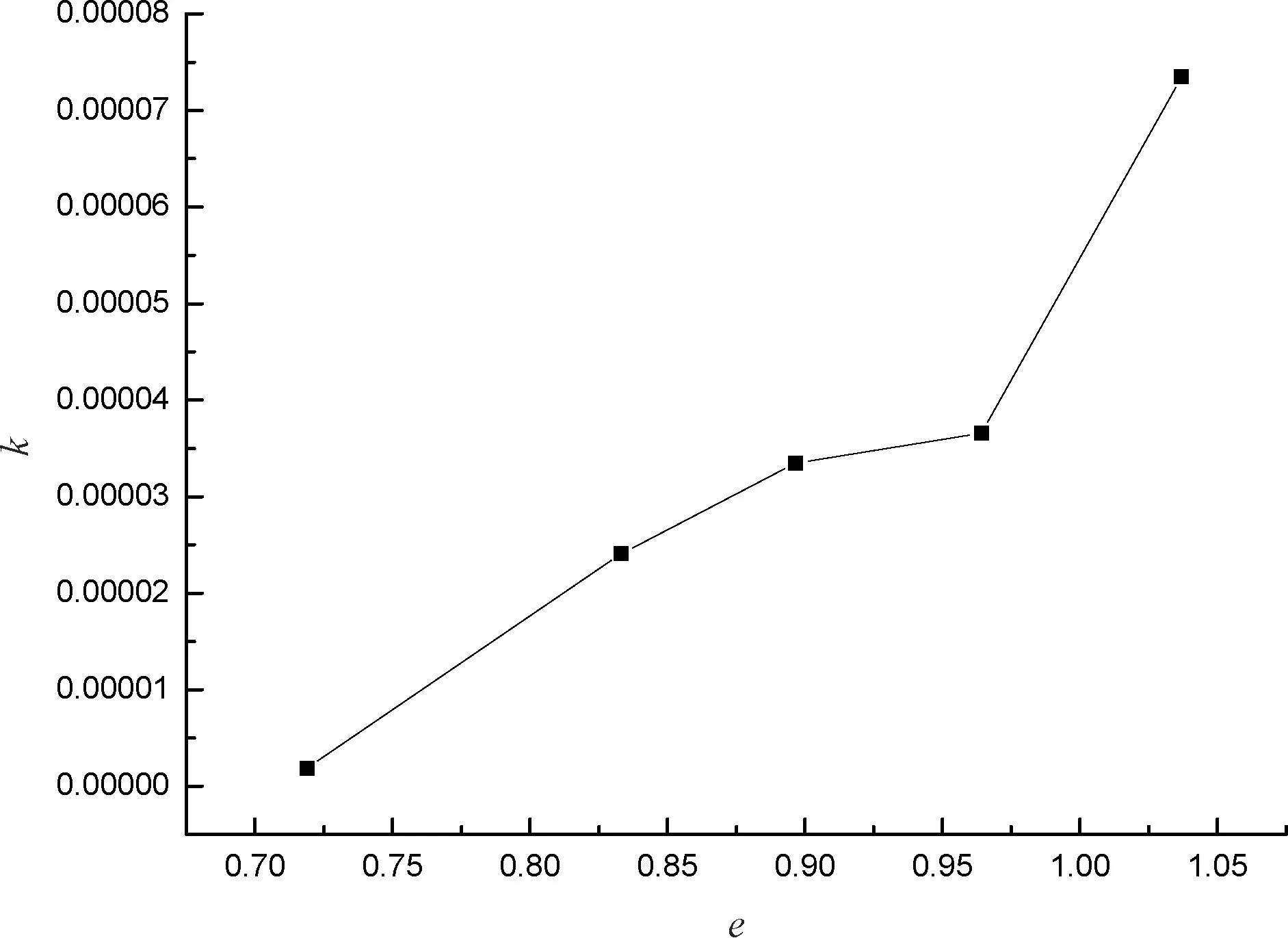
图2　试样孔隙比e与渗透系数k的关系曲线

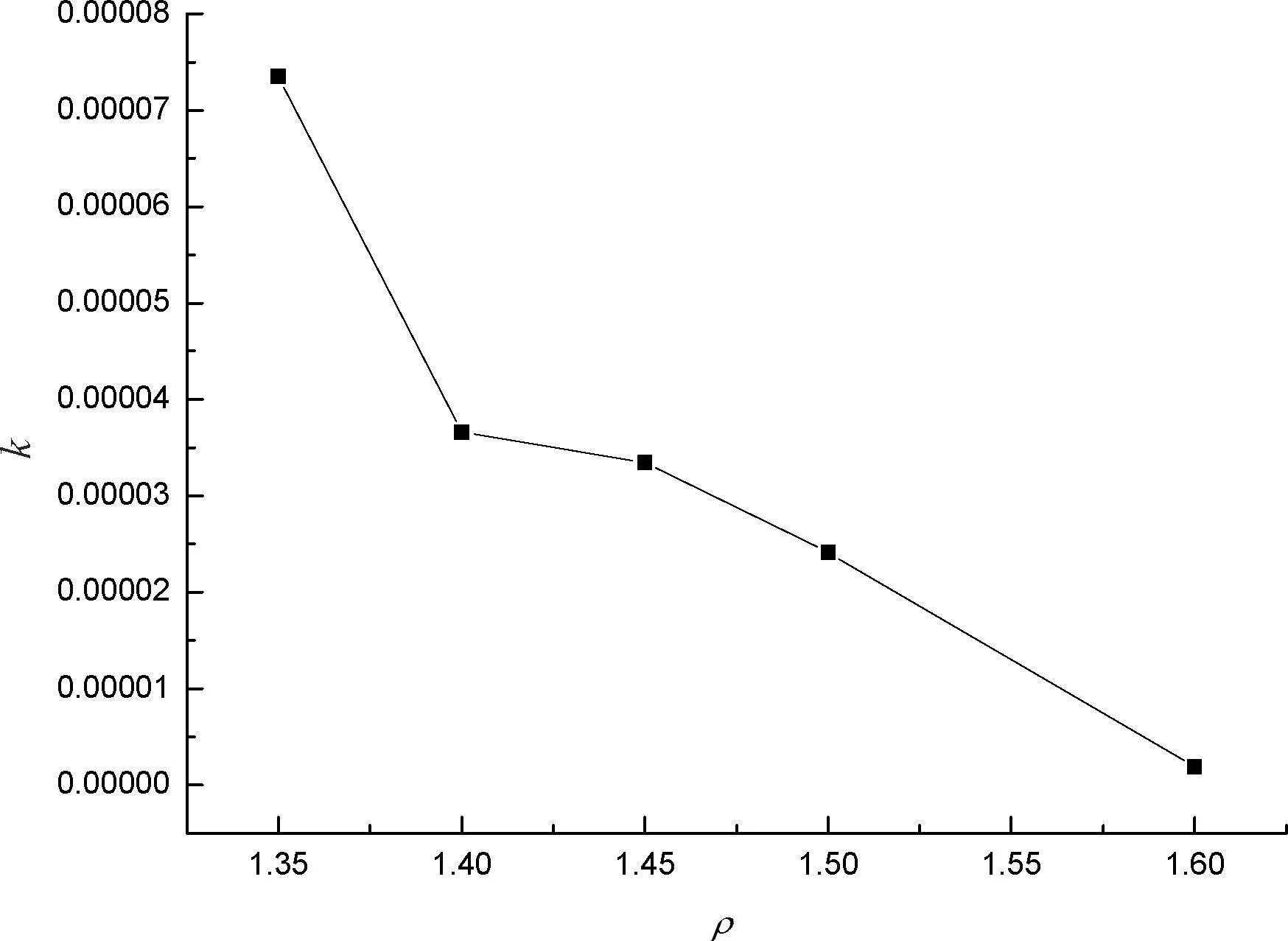
图3　试样干密度ρd与渗透系数k的关系曲线

从图2可知渗透系数k随着孔隙比e的增大而增大，主要分为3个区域:当孔隙比e为0.718 8—0.833 3区域的试样，起初孔隙孔径较小，但其孔隙率慢慢变大，孔隙孔径也逐渐增大；当孔隙比e为0.833 3—0.964 3时，土体孔隙比进一步增大，但是渗透系数增加不多；当孔隙比为0.964 3—1.037 0区域的试样，土体密实度最小，孔隙孔径最大，水在渗透过程中受到的颗粒间阻力是最小的，所以渗透系数是最大的。

从图3可知，渗透系数k随着黏土试样干密度ρd的增大而减小，主要分为3个区域:当干密度在1.35—1.40时，干密度逐渐增加，土体孔隙孔径由最大逐渐减小，同样渗透系数也是逐渐减小；当干密度在1.40—1.50时，干密度逐渐增加，但渗透系数变化不大；当干密度在1.50—1.60时，干密度增加到最大，土体孔隙孔径是最小的，渗透系数是最小的。

对重塑黏性土试样进行变水头渗透试验，进行黏土试样的渗透系数k与孔隙比e和土体干密度ρd的关系分析[8]。曾玲玲，洪振舜在对重塑黏性土的压缩过程中，对渗透系数的变化规律进行研究，发现随着重塑黏性土干密度ρd的增大和孔隙比e的减小，渗透系数k呈现指数级减小，可以通过e—lgk、lge—lgk以及lg(1+e)—lgk的单对数或双对数形式，特别研究渗透系数与孔隙比的关系，提出考虑不同重塑土基本物理指标的影响表达式，从而建立简单实用的关于渗透系数与孔隙比关系的预测公式[9]。研究本次变水头渗透试验的关系，通过已知e和k,得出对应的lge、lg(1+e)、lgk值，对数形式如表5所示。

表5e—lgk、lge—lgk、lg(1+e)—lgk对数形式

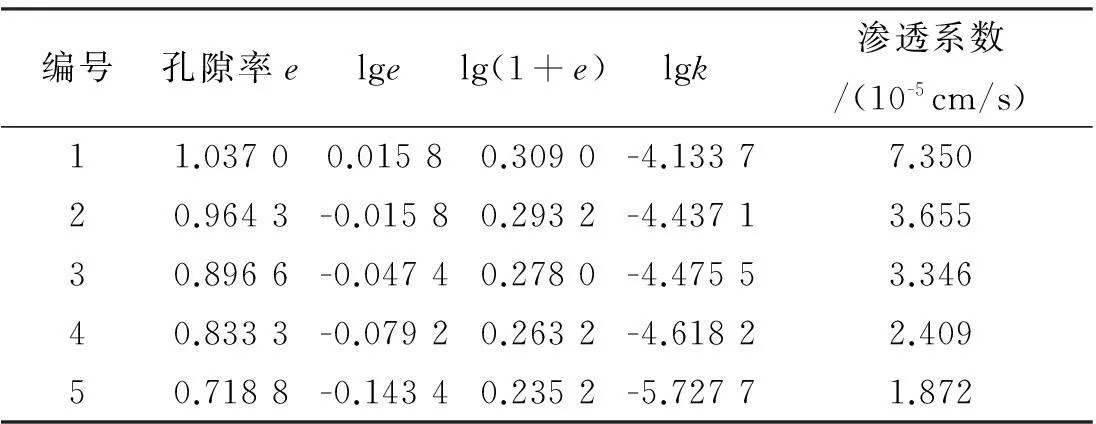
编号孔隙率elgelg(1+e)lgk渗透系数/(10-5cm/s)11.03700.01580.3090-4.13377.35020.9643-0.01580.2932-4.43713.65530.8966-0.04740.2780-4.47553.34640.8333-0.07920.2632-4.61822.40950.7188-0.14340.2352-5.72771.872

根据表中数据得出试样的e—lgk、lge—lgk以及lg(1+e)-lgk的单对数或双对数关系曲线图，如图4—图6所示。

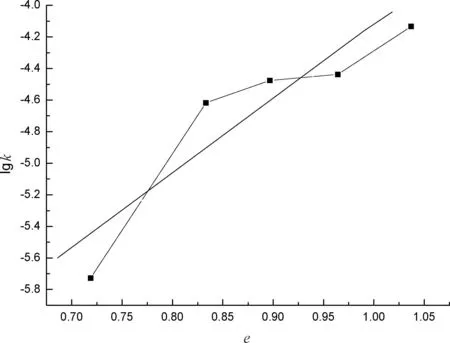
图4　不同干密度的试样lgk—e的半对数关系图

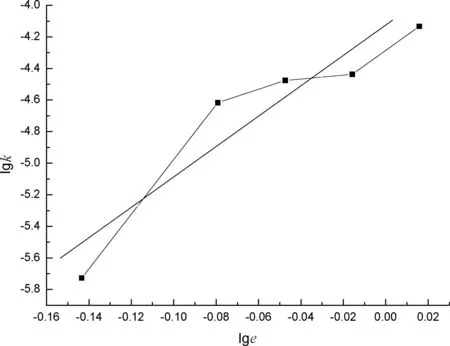
图5　不同干密度的试样lgk—lge的双对数关系

由图4可知，孔隙比e与lgk呈直线关系，其斜率为孔隙比e的函数，这一经验关系式位于数据点的中间，总体上具有很好的相关性，利用origin绘图软件对孔隙比e与lgk的坐标关系曲线进行拟合，拟合的曲线关系式：

y=-8.78671+4.61604x.

(13)

其线性相关系数R为0.920 65，y是对渗透系数k取的对数，即lgk，x是试样土体的孔隙比e。

由图5可知，lge与lgk呈直线关系，其斜率为孔隙比lge的函数，这一经验关系式位于数据点的中间，总体上具有很好的相关性，对lge与lgk的坐标关系曲线进行拟合，拟合的曲线关系式：

y=-4.17139+9.38975x.

(14)

其线性相关系数R为0.938 81，y是对渗透系数k取的对数，即lgk，x是对试样土体的孔隙比e取的对数，即lge。不同干密度试样lgk—lg(1+e)的双对数关系如图6所示。

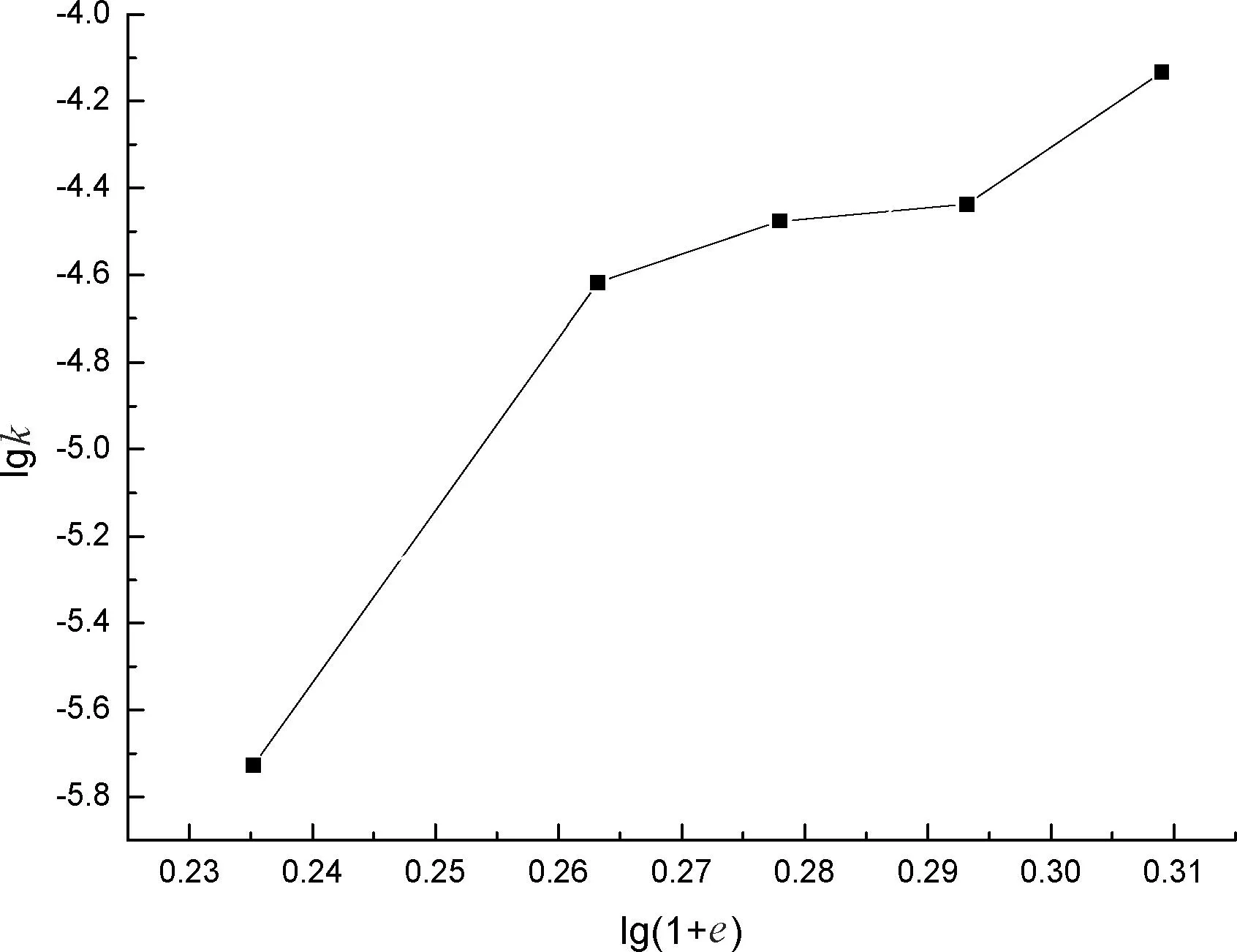
图6　不同干密度试样lgk—lg(1+e)的双对数关系图

由图6可知，lg(1+e)与lgk的呈直线关系，其斜率为孔隙比lg(1+e)的函数，这一经验关系式位于数据点的中间，总体上具有很好的相关性，对lg(1+e)与lgk的坐标关系曲线进行拟合，拟合的曲线关系式：

y=-10.21286+20.07259x.

(15)

其线性相关系数R为0.929 33，y是对渗透系数k取的对数，即lgk，x是对(1+e)取的对数，即lg(1+e)。

结果表明，几种关系式反映了渗透系数与孔隙比呈直线关系，以对数形式表示的lgk—lg(1+e)和lgk—lge的双对数形式得到的相关性系数，要高于半对数形式lgk—e所得到的相关性系数。并且线性相关性的大小顺序为lgk—lge>lgk—lg(1+e)>lgk—e。关系曲线位于数据点的中间，总体上具有很好的相关性，说明lgk—lge所得到的拟合曲线关系(14)对试样的渗透系数与孔隙比关系的描述最好。

4结束语

笔者采用变水头法试验对黏性土试样进行渗透系数的测量。由曲线知：随着黏性土孔隙比e逐渐增大即土的干密度ρd逐渐减小，则渗透系数k也逐渐增大。得出渗透系数k与孔隙比e的3种关于lgk—lge、lgk—lg(1+e)、lgk—e半对数或双对数关系曲线图以及对应的关系式，渗透系数与孔隙比呈直线关系，通过对比分析知道lgk—lge的线性相关性最显著。本试验只研究了土体孔隙比与其渗透系数之间的关系，但孔隙比并不能完全反映土体孔隙结构的情况，所以试验研究中还要考虑土体其它参数，如液限、土体的含水比等对其渗透系数的影响。本文中许多关系曲线在拟合时为了研究与运算的方便，笔者只是做了简单的线性拟合，并没有考虑比较复杂的折线与非线性拟合[10]。

参考文献：

[1]张力霆,齐清兰,魏静,等.淤填黏土固结过程中孔隙比的变化规律[J].岩土力学, 2009, 30(10).

[2]李广信.对与基坑工程有关的一些规范的讨论(3)[J].工程勘察, 2013(11):1-4.

[3]土工试验技术手册[M].北京:人民交通出版社, 2003.

[4]唐朝生,施斌,刘春,等.黏性土在不同温度下干缩裂缝的发展规律及形态学定量分析[J]. 岩土工程学报, 2007, 29(5): 743-749.

[5]符二东.变水头法测定渗透系数试验方法分析及探讨[J].山西建筑,2014,40(2): 68-69.

[6]刘松玉.土力学[M]. 北京:中国建筑工业出版社, 2005.

[7]李聪,吴建林,陈珑.纳米蒙脱土对软黏土性能影响的试验[J].武汉轻工大学学报, 2014, 33(2): 72-76.

[8]包孟碟,何翔.基于砂岩 CT 图像的渗透系数数值模拟研究[J]. 江西建材, 2015 (13): 1-2.

[9]曾玲玲,洪振舜,陈福全.压缩过程中重塑黏土渗透系数的变化规律[J].岩土力学,2012,33(5):1286-1292.

[10]黄发兴,陆海军,陈威,等.饱和—非饱和填埋场衬垫系统中水渗流规律的数值模拟[J]. 武汉工业学院学报, 2013, 32(4): 69-73.

Cohesive soils’s permeability analysis under different compactness

CHENZong-xian,HEXiang,XIONGYun-shan,WANGRui

(School of Civil Engineering and Architecture , Wuhan Polytechnic University, Wuhan 430023, China)

Abstract：Soil mass is a material with complex physical properties,and the microscopic pore characteristics of the soil determine the permeability of the soil. So the physical properties of soil are determined. The permeability and porosity of soil are analyzed in this paper, using variable head permeability test. Main research task: the soil sample was prepared from a Wuhan site, to measure its physical index, for dry sieving,and to prepar remodeling sample by static pressure test, for penetration testing. Analysis results show that: With the increasing of the clay pore ratio e and dry density of soil gradually decreasing, the permeability coefficientkincreases gradually.And the various experience relationship between permeability coefficient and void ratio are compared.

Key words：permeability coefficient; void ratio; penetration test; remodeling sample

收稿日期：2015-12-02.修回日期：2015-12-24.

作者简介：陈宗先(1990-)，男，硕士研究生，E-mail: 1007447368@qq.com. 通信作者：何翔(1974-)，男，副教授，E-mail: hexiangchn@163.com.

文章编号：2095-7386(2016)02-0067-05

DOI:10.3969/j.issn.2095-7386.2016.02.012

中图分类号：TU 411

文献标识码：A