基于区域均衡和压缩因子的混合粒子群算法的研究

陈　欣,刘　朔

(武汉轻工大学 数学与计算机学院，湖北 武汉 430023)



基于区域均衡和压缩因子的混合粒子群算法的研究

陈欣,刘朔

(武汉轻工大学 数学与计算机学院，湖北 武汉 430023)

摘要：针对传统粒子群算法容易陷入局部最优解的问题，提出一种在采用全局最优和区域均衡最优相结合来共同更新粒子速度的基础上，融合压缩因子的混合算法。将粒子的局部区域均衡的信息加入到速度更新公式，使得粒子的速度同时受到全局最优和区域平衡最优的作用，提高了粒子的寻优性能，平衡粒子的全局寻优能力和局部寻优能力。通过选取几个多峰值的测试函数进行仿真实验，表明该算法粒子的寻优性能有较大优势。

关键词：混合粒子群算法;区域均衡;压缩因子

1引言

在众多群体智能算法中，粒子群算法的结构简单，易于实现，并有着非常广泛的应用。但是，粒子群算法和其他的智能算法一样，也存在陷入局部最优解的弱点。为了克服这些弱点，很多学者提出了不同的改进方案。马国庆等[1]提出了利用惯性权重线性递减的策略。任圆圆[2]给出非线性的动态惯性权重设置即自适应权重的公式。Shi Y等[3]则从控制微粒的飞行速度入手，构造了设置压缩因子的改进粒子群算法，都取得了一定的效果。以上这些算法，粒子速度的更新仍然极大取决于自身最优解和全局最优解，容易出现早熟的现象。本文提出一种混合粒子群算法，在微粒的速度更新公式中引入区域均衡最优解和飞行速度控制的压缩因子，使得粒子速度的更新更为合理，使混合粒子群算法的搜索能力和收敛精确度进一步增强。

2标准的粒子群算法

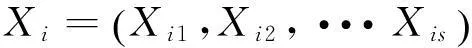
(1)

而第i个粒子的速度和位置更新见式(2)和式(3)：

Vi(t+1)=Vi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pg(t)-xi(t)).

(2)

xi(t+1)=xi(t)+Vi(t+1).

(3)

其中c1,c2是非负常数，r1,r2是相互独立的随机数，Vi∈[-vmax,vmax]，其中vmax由用户根据实际问题具体设定。迭代的终止条件一般选定为最大迭代次数T。

3引入区域均衡最优解和压缩因子的混合粒子群算法

3.1融合区域均衡的最优解

传统粒子群算法中，种群中的每一个粒子的速度更新都是依赖于该粒子本身的历史最优解和整个种群的最优解。在传统粒子群算法的前期搜寻阶段，很有可能会出现粒子搜寻过快，与最优解擦肩而过的情况，这样接下来的搜寻就很容易陷入局部最优的陷阱。陈群林等[5]为了提高算法搜寻的准确度，针对粒子群算法局部搜寻能力引入了粒子加速和变异的机制。张水平等[4]就提出一种用每个粒子的邻居的当前最优解代替全局最优解来平衡局部搜索能力的方案，但是这种做法仍然具有一定的局限性，特别是每个粒子之间的距离的计算和存储将会使得算法的运算时间和存储空间的花销大大增加。本文把该粒子作为一个局部区域的中心，设定一个圆形的邻域，以该邻域内部所有粒子的当前最优位置的几何中心Pn作为该区域内的全局最优位置，这样，每个粒子周围的局部信息将得到更加高效和准确的传递。即使在最极端的情况下，可能出现在所给邻域内并没有出现其他的粒子，这样邻域的范围就也应该做出相应的扩大调整。邻域扩大过程如下：

r=k;

search=1;

while count==0 or search!=3;

r=1.5*r;

search=search+1.

如果三次调整后，周围仍然没有其余粒子出现，恰好说明该粒子周围局部信息不足，无需平衡，此时直接应用原始的速度更新公式即可。综合以上的讨论，本文提出一个基于局部范围内区最优解的速度更新公式为：

Vi(t+1)=Vi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pn(t)-xi(t)).

以往的研究表明，传统的全局PSO算法收敛速度快，但容易陷入局部最优的陷阱[6]。而结合区域均衡最优解的搜索算法可以搜索到相对更优更精确的解，但是搜索速度会更慢一些。因此，本文采用一种采用全局最优和区域均衡最优相结合来共同更新粒子速度的混合算法，公式如下：

Hi(t+1)=u1Mi(t+1)+u2Ni(t+1).

其中：

Mi(t+1)=Vi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pn(t)-xi(t))是针对局部均衡寻优。

Ni(t+1)=Vi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pg(t)-xi(t))是针对全局均衡寻优。

并且u1=t/T,u2=1-u1的设置可以保证算法在兼顾了局部寻优和全局寻优的情况下，前期粒子的速度不会太快以至于错过最优解，在算法后期也会更具有精确性。

3.2压缩因子

在速度更新的公式中，c1,c2这两个非负常数的值决定了微粒本身的经验和其他微粒的经验信息对运动轨迹的影响，反映了微粒之间的信息交流[7]。设置c1较大，会使微粒更多地在局部徘徊，而设置c2较大，又会使微粒过早收敛，为了达到全局探测和局部开采的两者间的平衡，Shi Y等[3]提出了设置收缩因子的策略，速度更新公式如下：

Vi(t+1)=φ{Vi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pg(t)-xi(t))}.

其中

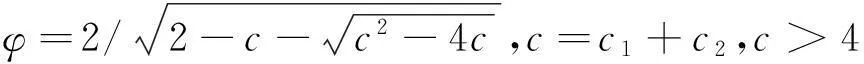
文献[3]提出的相比文献[1],[2]提出的针对权重的优化，设置压缩因子比权重系数，更能有效地控制约束微粒的飞行速度，同时增强了算法的局部搜索能力。本文对压缩因子的设置做了一定的改进，在控制了微粒飞行的速度的情况下，完整地保留对微粒间个体最佳适应值和全局最佳适应值信息的传递，更新后的速度更新公式如下：

Vi(t+1)=φVi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pg(t)-xi(t)).

其中

3.3区域均衡最优解和压缩因子的混合

本文在引入区域均衡最优解和设定压缩因子这两个方面，改进了粒子的更新公式和位置更新公式，提出了一种混合粒子群算法。新的速度和位置更新公式如下：

Mi(t+1)=φVi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pn(t)-xi(t)).

Ni(t+1)=φVi(t)+c1r1(Pi(t)-xi(t))+

c2r2(Pg(t)-xi(t)).

Hi(t+1)=u1Mi(t+1)+u2Ni(t+1).

Xi(t+1)=Xi(t)+Hi(t+1).

4仿真实验

为了测试本文算法的实际性能效果，将其与文献[1]提出的惯性权重线性递减算法与文献[2]提出的自适应权重算法经行实验比较，采用三个多峰值测试函数进行测试比较每个函数的参数设置如表1,表2,表3所示，算法测试结果如表4,表5,表6所示。

表1Ackley函数的初始参数设置

种群C1C2初始区间目标值迭代数401.51.5[-32,32]0100

表2Rastrigrin函数的初始参数设置

种群C1C2初始区间目标值迭代数401.51.5[-5.12,5.12]0100

表3Schaffer函数的初始参数设置

种群C1C2初始区间目标值迭代数401.51.5[-10,10]0100

三个多峰测试函数[8]如下。

Rastrigrin函数：

Schaffer函数:

表4对于Ackley测试函数的不同算法运行结果

项目惯性权重递减的PSO算法自适应权重调整的PSO算法本文算法算法运行次数303030算法平均运行时间/s0.07600.07860.2323最佳平均适应度/10-6-0.525-0.539-0.255

表5对于Rastrigrin测试函数的不同算法运行结果

表6对于Schaffer测试函数的不同算法运行结果

项目惯性权重递减的PSO算法自适应权重调整的PSO算法本文算法算法运行次数303030算法平均运行时间/s0.06920.06670.2011最佳平均适应度/10-6-0.423-0.512-0.105

本文选取的三个测试函数都是经典的多峰值测试函数，既可以对算法的准确度进行测试，也可以对算法的寻优精度进行评价。从图1，图2，图3可以看出，本文算法的收敛速度和寻优精度都是优于文献[1,2]提出的针对权重调整的算法。而且本算法的鲁棒性较好，不容易掉入局部最优的陷阱。

图1　 Ackley函数测试图

图2　Rastrigrin函数测试图

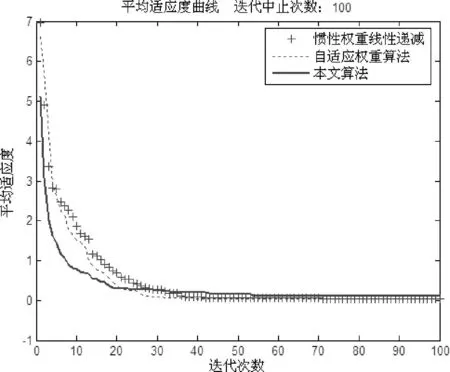
图3　Schaffer函数测试图

5结束语

针对传统粒子群算法容易陷入局部最优的问题，提出一种混合粒子群算法，在微粒的速度更新公式中引入区域均衡最优解和飞行速度控制的压缩因子，将全局最优解和区域平衡最优解的影响因素同时用于更新粒子的速度。实验表明，本文算法在优化能力和性能上都有了很大的提高,但是算法的运行速度和稳定性还有待于进一步提高。

参考文献：

[1]马国庆，李瑞峰，刘丽.学习因子和时间因子随权重调整的粒子群算法[J].计算机应用研究，2014，31(11)：3291-3294.

[2]任圆圆，刘培玉，薛素芝.一种新的自适应动态文化粒子群优化算法[J].计算机应用研究，2013，30(11)：3240-3243.

[3]Shi Y，Eberhart R C.Empirical Study of Particle Swarm Optimization[C]//Proc of Congress on Evolutionary Computation.1999.

[4]张水平，仲伟彪.改进学习因子和约束因子的混合粒子群算法[J].计算机应用研究, 2015,32(12)：3626-3628.

[5]陈群林,高岳林,郭祥.一种带有加速策略和变异策略的粒子群算法[J].兰州文理学院学报(自然科学版),2015,29(6)：41-47.

[6]孙振龙,李晓晔,王颖.一种改进的简化粒子群优化算法[J].计算机科学,2015,42(11A)：86-88.

[7]冯浩,李现伟.一种改进的粒子群优化算法惯性权值递减策略[J].蚌埠学院学报,2015,4(6)：21-24.

[8]宋锦,高浩.基于双重更新策略的粒子群算法[J].南京邮电大学学报(自然科学版),2015,35(6)：84-88.

Hybrid particle swarm optimization algorithm of regional equilibrium and compression factor

CHENXin,LIUShuo

(School of Mathematics and Computer Science, Wuhan Polytechnic University, Wuhan 430023,China)

Abstract：In order to avoid traditional PSO algorithm converging too fast and easily falling into local optimum value, the PSO algorithm is proposed with regional equilibrium and global optimal value, adding the regional equilibrium optimum value into the updating formula of particle speed, and improving the search ability of the particle.Compared three classic test function, the algorithm can greatly improve the search ability of the particle.

Key words：hybrid particle swarm optimization; regional equilibrium; compression factor

收稿日期:2016-03-04.修回日期:2016-03-31.

作者简介:陈欣(1978-),男,讲师,E-mail:2924892402@qq.com.

文章编号：2095-7386(2016)02-0083-04

DOI:10.3969/j.issn.2095-7386.2016.02.015

中图分类号：TP 301.6

文献标识码：A