软土路基病害机理及Boltzmann沉降模型应用研究

刘江波, 李　俊

(1.海南省公路勘察设计院, 海南 海口, 570206;　2.长安大学 公路学院, 陕西 西安　710064)



软土路基病害机理及Boltzmann沉降模型应用研究

刘江波1, 李俊2

(1.海南省公路勘察设计院, 海南 海口, 570206;2.长安大学 公路学院, 陕西 西安710064)

[摘要]针对海南省滨海公路软土路基工程地质特征，采用统计调查的方法，分析了软土路基与路面病害相关性，并通过建立Boltzmann沉降模型，采用微分方法，结合沉降曲线几何意义，分析了软土路基沉降发育规律。结果表明：软土路基与路面病害具有直接相关性，但排水条件好的软土路段，由于其固结及隔离作用，病害与一般路段相比并不严重；采用微分方法对Boltzmann模型进行三阶导数分析，得到软土路基沉降发育各阶段的区间计算公式；采用相对误差分析Boltzmann模型预测沉降值与实测沉降值之间的差异，验证了模型的适用性。

[关键词]软土路基； 病害机理； 沉降规律； Boltzmann模型

0前言

软土路基处治是公路建设中遇到的最为常见的特殊路基工程处理技术问题。通过建立软土路基沉降与时间关系模型，预测软土路基堆载期间以及工后沉降，是解决软土路基病害发生的有效途径[1]。利用土的本构模型，采用Biot固结理论进行沉降预测与工程实际存在较大差距，预测结果难以令人满意，因此应用并不广泛[2]；根据实测沉降数据推算沉降与时间关系的预测方法，如双曲线法、对数曲线法、多项式法、S型成长曲线法等，对于预测路基沉降的发展规律起到极大的促进作用[3-5]。其中S型成长曲线的特点与路基沉降发展规律存在相似之处，而且形式多样，基本上可以满足不同土质路基沉降预测模型建立要求。

李明飞[6]采用理论分析、现场试验和数值模拟相结合的方法，对高速公路软土路基的变形规律进行了研究；付宏渊[7]分析了路基沉降计算得影响因素，并以工程实例说明了曲线拟合法预测路基沉降的合理性；何良德[8]等结合高速公路水准网精度低于沉降观测精度要求的特点，提出和研究了拟附合水准路线的平差和精度估计方法；赵明华[9]等结合5种常用的成长模型，提出了滨海公路软土路基变权重组合S型成长模型；朱志铎[10]等建立软土路基全过程沉降预测的Logistic模型，确定了模型中各参数含义，分析了各参数对地基沉降不同阶段的影响。然而根据软土路基沉降发展规律，推算沉降发生各阶段的时间区间，目前仍是软土路基研究的空白区域。

本文针对海南早期建成的滨海公路破坏特征与软土路基关系的调查，分析浜塘区软土路基的破坏特征，并对其工后沉降进行监测，通过建立BoltzmannS型预测模型，推算软土路基沉降发展各阶段的时间区间。

1工程地质概况

海南省隆丰至三江公路项目建成于上世纪七十年代，历经多次维修，全线路基基本为低填浅挖，最大填挖高度均小于8m。路基较稳定，未见滑移、沉陷等现象。根据地形、地貌、地层结构及工程地质条件复杂程度，将全线划分为工程地质2个大区，3个小区。①Ⅰ1路段(K4+184～K7+364)为海成一级阶地，分布杂填土(Qml)、高液限淤泥质粉质粘土(Q4m)、低液限粉质粘土(Q3m)，其中前两者均匀性差，工程性能差，未经处理，不宜直接作为拟建道路路基持力层；后者均匀性较好，工程性能较好，可作为拟建道路路基持力层。②Ⅱ1路段(K0+016～K4+184)，海成二级阶地，分布杂填土(Qml)、高液限淤液泥质粉质粘土(Q4m)、低液限粉质粘土(Q3m)、低液限粉质粘土(Qel)、中风化花岗岩(K2γ)，其中前三者性质同Ⅰ1路段，均匀性差，工程性能差，未经处理，不宜直接作为拟建道路路基持力层；后两者均匀性好，岩土性质好，可作为拟建道路路基持力层。③Ⅱ2路段(K7+364～K18+967)，海成二级阶地，分布杂填土(Qml)、高液限淤液泥质粉质粘土(Q4m)、低液限粉质粘土(Q3m)、低液限粉质粘土(Qel)、中风化花岗岩(K2γ)、强风化花岗岩(T2γ)，其中前五者性质同Ⅰ1路段，均匀性差，工程性能差，未经处理，不宜直接作为拟建道路路基持力层；后者均匀性好，岩土性质好，可作为拟建道路路基持力层。

2路面病害与软土特性相关性分析

海南省隆丰至三江公路项目隆丰至三江公路、锦山至罗豆公路路面宽均为6～6.5m，为九十年代大修的沥青表处路面，因超龄服务，现状多松散、沉陷、波浪拥包、坑槽，平整度极差，并存在不规则纵横向裂缝及修补痕迹。为进一步分析滨海公路病害与软土之间的关系，对隆丰至三江公路软土段路基病害中普遍发生的路面网裂、路基翻浆病害进行统计分析，选择易于量化的网裂发生率和翻浆发生段作为统计依据，开展了隆丰至三江公路全线路基的病害调查。

根据隆丰至三江公路全线路基的病害调查统计数据，做出路面网裂发生率、翻浆发生段与软基分布关系，见图1、图2。

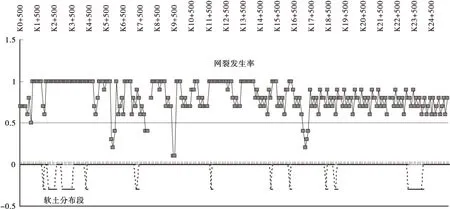
图1　路面网裂发生率与软基关系Figure 1　Relation of net-shaped crack with soft clay embankment

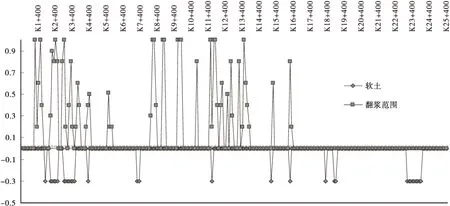
图2　路面翻浆发生段与软基分布关系Figure 2　Relation of frost boiling with soft clay embankment

由图1、图2可知: 调查路段路面网裂发生率、翻浆发生段与软基分布呈现直接相关关系，小桩号路段相关性尤甚。由于建设时对于分布于硬壳层以下的滨海软土及厚度较大的滨海软弱土层路基未作系统处理，以致小桩号段软土分布的低洼区，发生了严重的全断面路面网裂、路基沉陷、路面翻浆病害，说明了软土路基处治的重要性；另一方面，位于大桩号段的软基，由于地形条件有利于路基排水，滨海相软土具有较高的渗透系数，软土路基能在路面形成后完成固结作用，加上后期对网裂的修补能发挥封闭隔水作用，路面病害如网裂与翻浆等明显相对较轻，因此，软土路基分布区并未发生比正常路基更严重的路面病害，说明用排水固结方法是可用于处理滨海公路软土路基可行的方法。

3Boltzmann模型的提出

3.1BoltzmannS型成长曲线模型

图3示出的是海南省万宁石梅湾至大花角旅游公路工后沉降实测曲线，从该地区软土路基沉降与时间过程曲线可以看出：沉降发展基本上经历了“发生→发展→稳定→极限”的过程，呈现S型曲线过程。

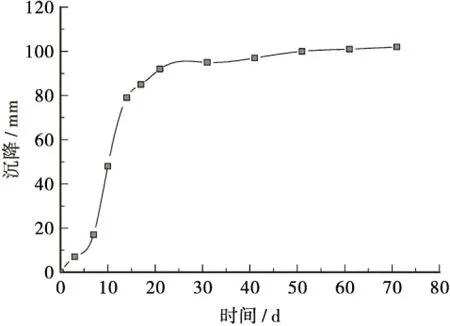
图3　石梅湾至大花角旅游公路工后沉降实测曲线Figure 3　Measured settlement curve in Shimeiwan to Dahuajiao tourist highway

S型成长曲线多用于自然社会经济预测中，亦称成长曲线。成长曲线反映的实际是事物发生、发展、成熟，然后达到一定极限的过程，所以往往能比简单时间序列法提供更加精确的时间预测。本文以BoltzmannS型成长曲线为例，对软土路基工后沉降发展过程各阶段的时间区间进行分析。

3.2沉降发展区间计算模型

BoltzmannS型成长曲线模型基本形式如式(1)所示。

(1)

式中： A1、A2、x0、dx为模型4个参数，其中A1、A2为模型两条渐近线，分别为初值、终值；x0为模型拐点，是成长曲线凹凸突变点；dx为模型时间常量，与模型从初值改变到终值的速度有关。由S型成长模型的特性，如单调递增性、不过原点性、有界性以及存在反弯点，可以看出它能较准确地反映软土地基固结沉降的变化规律。

对于BoltzmannS型成长曲线模型，分别对其进行一阶、二阶、三阶求导，可得到式(2)～式(4)。

(2)

(3)

(4)

令y(2)=0、y(3)=0，可得BoltzmannS型成长曲线模型的特征点x1=x0、x2=+ln(2±)dx。x1为BoltzmannS型成长曲线模型由凹曲线拐向凸曲线的中间点，表征软土路基沉降由快速发展到缓慢成长过渡的特征点。x2为BoltzmannS型成长曲线模型任一点切线斜率变化率的零点，表征软土路基沉降变化的缓急，结合软土路基工后沉降实测曲线以及三阶导数几何意义，本文认为x2为软土路基沉降发展各阶段的临界点，亦即沉降发展各阶段的区间分界点。因此得到基于Boltzmann模型的软土路基沉降值S的发展各阶段的计算公式，见式(5)。

(5)

4工程实例分析

项目组对用浅层垫层法处治后的海南省万宁石梅湾至大花角旅游公路软土路基工后沉降进行监测，选取K8+360、K9+590两个测点，监测结果见表1所示。

Origin软件具有强大的线性回归与曲线拟合功能，本文采用origin8.6软件，通过“Analysis→Fitting→Nonlinearcurvefit”中“Growth/Sigmoidal”功能，实现软土路基沉降数据的BoltzmannS型成长曲线拟合见图4、图5，拟合曲线的参数以及相关性见表2。

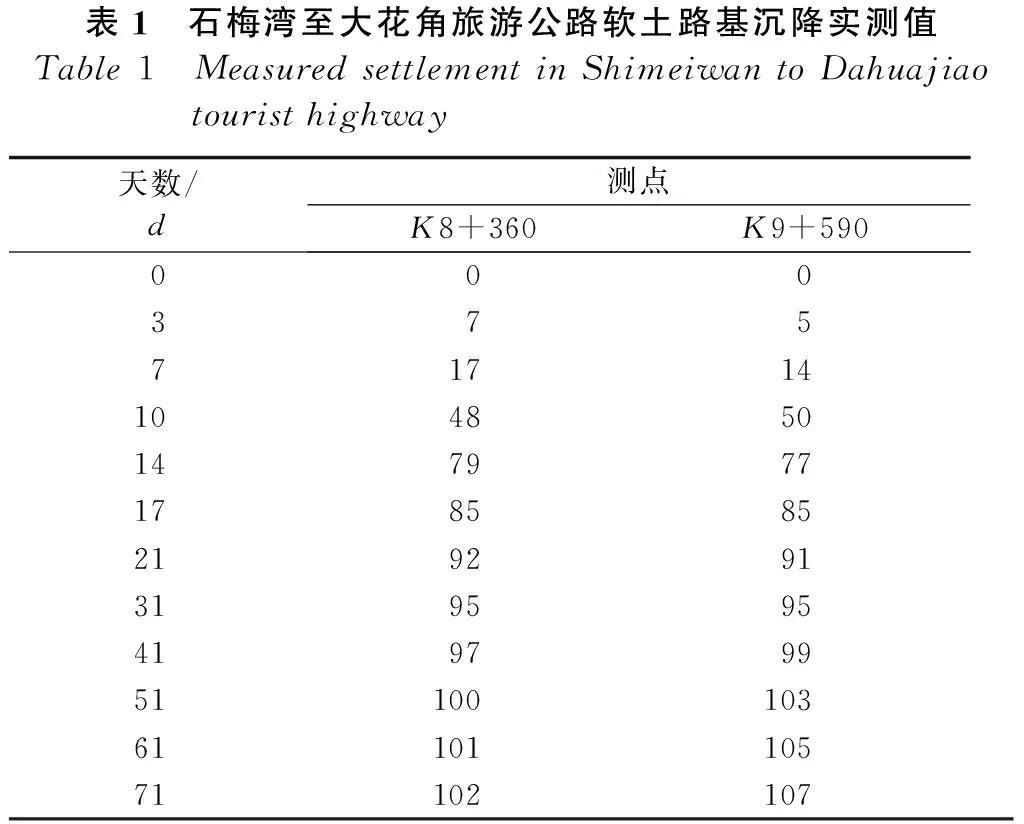
表1 石梅湾至大花角旅游公路软土路基沉降实测值Table1 MeasuredsettlementinShimeiwantoDahuajiaotouristhighway天数/d测点K8+360K9+59000037571714104850147977178585219291319595419799511001036110110571102107

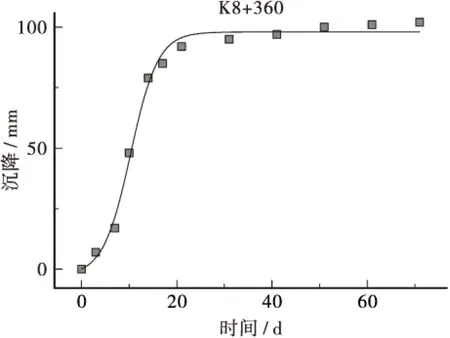
图4　测点K8+360 Boltzmann模型拟合曲线 Figure 4　Fitting curve with Boltzmann model in K8+360

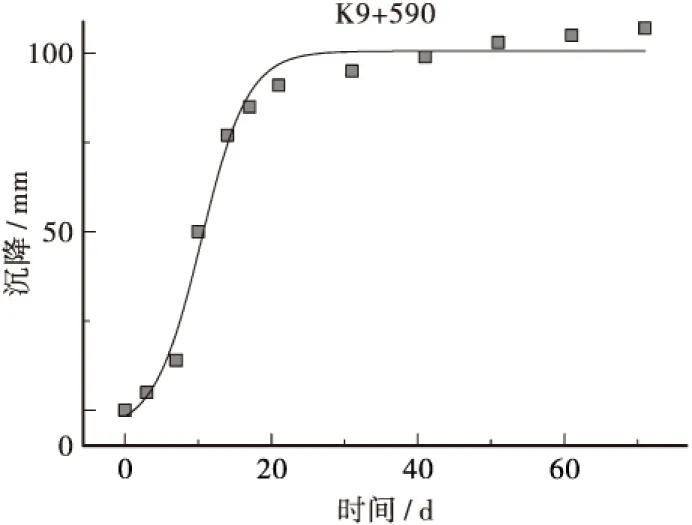
图5　测点K9+590 Boltzmann模型拟合曲线Figure 5　Fitting curve with Boltzmann model in K9+590

表2 BoltzmannS型成长曲线拟合参数表Table2 FittingparametersofsigmoidalgrowthcurvewithBoltzmannmodel测点参数A1A2x0dxR2残差平方和K8+360-2.6495798.0183810.279912.872070.99111110.98563K9+590-5.71242100.6019610.389553.201160.98159247.99079

4.1沉降发展区间计算

①K8+360测点沉降发展区间计算。

将表2中测点K8+360沉降实测数据拟合曲线参数代入式(1)，可得其BoltzmannS型成长曲线公式，见式(6)。

(6)

将拟合曲线参数代入式(5)，可得测点K8+360沉降发展各区间沉降值S计算结果，见式(7)。

(7)

②K9+590测点沉降发展区间计算。

将表2中测点K9+590沉降实测数据拟合曲线参数代入式(1)，可得其BoltzmannS型成长曲线公式，见式(8)。

(8)

将拟合曲线参数代入式(5)，可得测点K9+590沉降发展各区间沉降值S计算结果，见式(9)。

(9)

由上可知: 分布于相近地质条件区域内的2个测点K8+360与K9+590，采用Boltzmann模型计算得到的沉降发展区间具有很好地相关性，沉降发生阶段区间分别为(0，6.49751]与(0，6.17375]，发生阶段终值仅相差0.32396d，相对误差分别为5.0%、5.2%；沉降发展阶段区间分别为(6.49751，14.06237〗与(6.17375，14.60535〗，发展阶段终值仅相差0.54202d，相对误差分别为3.9%、3.7%。

4.2Boltzmann模型的适用性

以测点K8+360为例，将不同工后时间代入式(6)，得到Boltzmann沉降预测模型下的不同时间软土路基沉降值，并与实测沉降值进行对比，结果如表3及图6所示。

由图6可知: 随着工后日期的延续，Boltzmann模型沉降预测值相对误差基本呈现减小的趋势，相对误差由第3天的32.1%逐步降低至第14天时3.3%后趋于稳定，这与软土路基沉降发展规律相应关联，由4.1小节可知: 工后近第6天和15天，是测点K8+360路段沉降发育的发展阶段，软土路基的固结沉降主要发生在此阶段，Boltzmann模型沉降预测值相比实测值最易发生较大偏差，因此相对误差较大的特点在这一阶段也最为明显。但随着工后

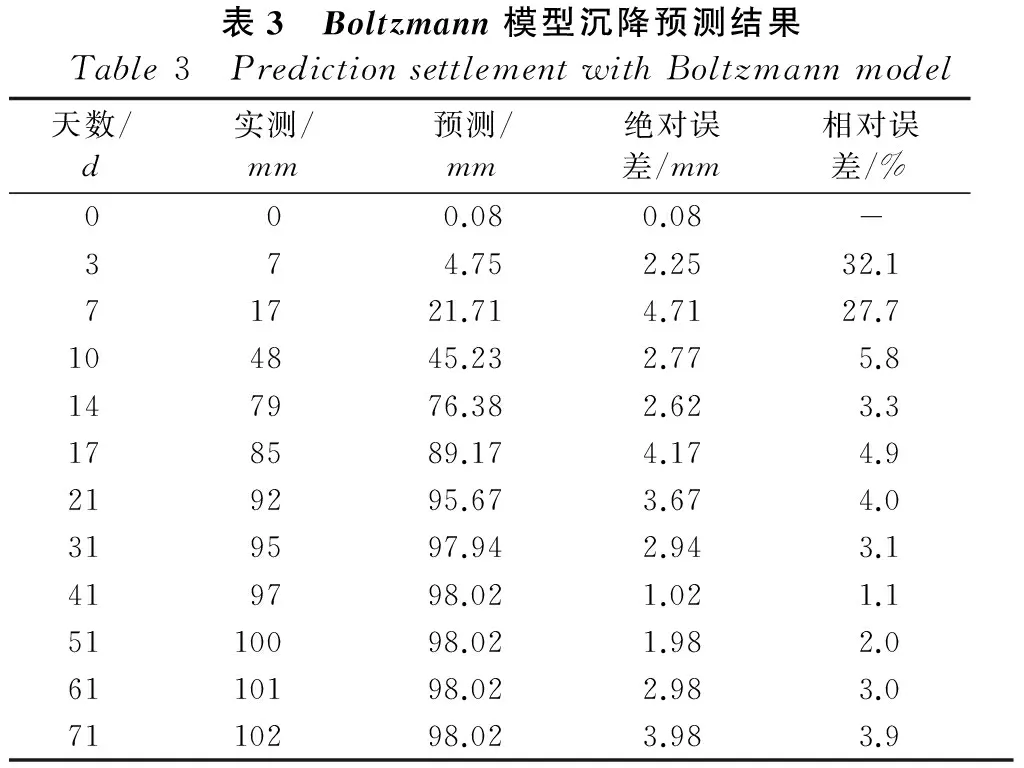
表3 Boltzmann模型沉降预测结果Table3 PredictionsettlementwithBoltzmannmodel天数/d实测/mm预测/mm绝对误差/mm相对误差/%000.080.08374.752.2532.171721.714.7127.7104845.232.775.8147976.382.623.3178589.174.174.9219295.673.674.0319597.942.943.1419798.021.021.15110098.021.982.06110198.022.983.07110298.023.983.9

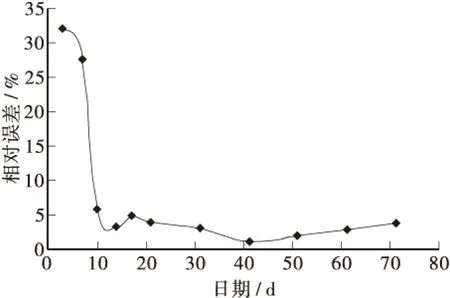
图6　Boltzmann模型沉降预测相对误差Figure 6　Relative error of prediction settlement with Boltzmann model

日期的延续，软土路基沉降发育趋于稳定，而Boltzmann模型沉降预测值也逐渐趋近于收敛值，故而预测值与实测值之间的误差也趋于稳定，逐渐收敛于某一固定值。

5结论

① 软土路基与路面网裂、翻浆等病害具有直接相关性，但排水条件较好的软土路段，软土具有较高的渗透系数，能在路面形成后完成固结作用，后期也能发挥封闭隔水作用，因此病害并不比一般路段严重。

② 采用微分方法对Boltzmann模型进行三阶导数分析，可得到软土路基沉降发育各阶段的区间计算公式，不同测点计算结果验证了其合理性。

③ 采用相对误差分析Boltzmann模型预测沉降值与实测沉降值之间的差异，预测值与实测值之间的差异与沉降发展规律保持一致性，验证了模型的适用性。

[参考文献]

[1]李红,韩尚宇,祝磊.软土路基工后沉降量影响因素比对分析

[J].公路工程,2013,8(4):5-8.

[2]DavisEH,RaymondGP.Anon-lineartheoryofconsolidation[J].Geotechnique, 1965, 15(2): 161-173.

[3]陈晖东,余湘娟,高磊.越南河内—海防高速公路路基沉降预测模型研究[J].公路工程,2014,4(2):16-19.

[4]胡振南.双曲线法在路基沉降预测中的应用研究[J].公路工程,2011,6(3):145-148.

[5]匡希龙,邹德强.基于龚帕斯曲线法的高填方路基工后沉降预测新思路[J].公路工程,2008,2(1):127-129.

[6]李明飞.高速公路软土路基变形规律研究[D].西安:西安科技大学,2006.

[7]付宏渊.路基沉降计算影响因素及预测方法研究[J].中外公路,2007,10(5):53-55.

[8]何良德,洪波,许永明,等.高速公路软土路基沉降观测的精度控制[J].公路,2003,4(4):74-78.

[9]赵明华,刘建华,刘煜,等.滨海公路软土路基变形机理及其沉降预测研究[J].公路交通科技,2006,1(1):32-35.

[10]朱志铎,周礼红.软土路基全过程沉降预测的Logistic模型应用研究[J].岩土工程学报,2009,6(6):965-969.

StudyonDamageMechanismandBoltzmannModelofSoftClayEmbankment

LIUJiangbo1,LIjun2

(1.HainanProvincialHighwaySurveyandDesignInstitute,Haikou,Hainan570206,China;2.Chang’anUniversityHighwayCollege,Xi’an,Shaanxi710064,China)

[Abstract]According to the geologic characteristics of soft clay embankment of coastal road in Hainan province and based on the method of statistical investigation, the correlation of soft clay embankment with pavement damage was analyzed. Also the settlement development regularity of soft clay embankment was analyzed through establishing the Boltzmann model, using the differential method and combining with the settlement curve geometric meaning. The results showed that the soft clay embankment correlated with pavement damage directly, but showed no serious difference for soft clay embankment with good drainage condition; The calculation formula of settlement development for soft clay embankment could be got through analysis of Boltzmann model based on differential method; Based on relative error method analyzed the different between predict settlement and measured settlement, and verified the applicability of the Boltzmann model.

[Key words]soft clay embankment; damage mechanism; settlement regularity; boltzmann model

[收稿日期]2015-03-18

[基金项目]海南省交通科技项目(JT20140898003)

[作者简介]刘江波(1981-)，男，湖南岳阳人，硕士，高级工程师，从事道路工程设计、科研工作。

[中图分类号]U 418.5

[文献标识码]A

[文章编号]1674-0610(2016)03-0203-05