基于MATLAB的机场道面不平度模拟技术研究

程国勇， 郭稳厚， 雷亚伟

(中国民航大学 机场学院， 天津　300300)



基于MATLAB的机场道面不平度模拟技术研究

程国勇， 郭稳厚， 雷亚伟

(中国民航大学 机场学院， 天津300300)

[摘要]为了研究飞机在道面激励下的振动反应，需要得到道面的纵断面曲线，即道面不平度。研究了基于谐波叠加法的道面不平度模拟方法；阐述了该方法的原理、特点；编制了运用该方法生成的随机道面谱程序；对3个不同等级的道面不平度进行了数字模拟，得到了相应道面等级的不平度序列。利用功率谱估计的方法对模拟道面谱和标准路面谱进行了比较，结果二者是一致的，表明谐波叠加法能很好的拟合道面不平度。

[关键词]道面不平度； 谐波叠加法； 功率谱密度； 软件开发

1概述

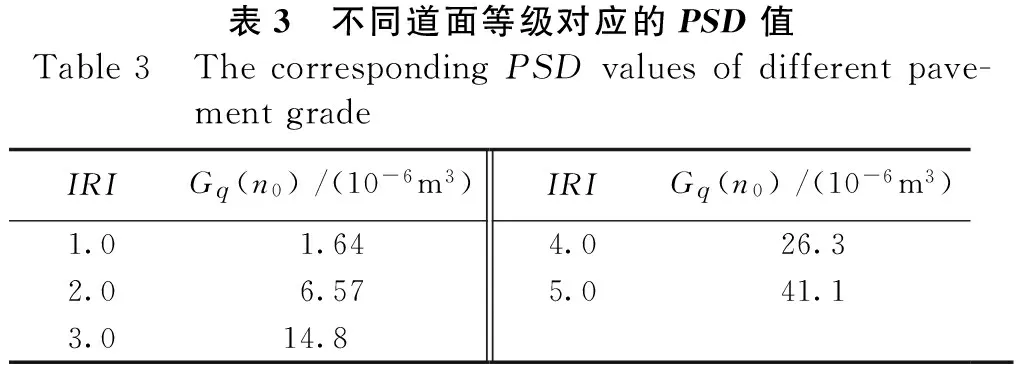
不平度是机场道面性能检测中非常重要的一项指标，对飞机的乘坐舒适度、滑行安全、燃油消耗及道面使用年限等有着重要影响。当飞机驶过平整程度较差的道面时，会引起机身振动，从而使乘坐的舒适度降低、货物受损、飞机的机械磨损加剧、航油消耗增加；另外飞机的附加振动会加大对道面的冲击作用从而缩减道面的适航服务年限。因此，对道面不平度研究的重要性日益被人们所重视。为了研究道面的不平度，首先要得到道面的不平度数据。道面不平度数据一般可以通过两种方法得到：一种是实际测量；另一种是通过计算机模拟得到道面不平度。早期对道面不平度的研究方法主要是实际测量，但该种方法比较费力、耗时多不经济[1]。而随着计算机技术的兴起，通过计算机对道面不平度进行模拟越来越为人们所接受和重视。目前，利用计算机模拟道面不平度的方法有很多种，较常用的理论方法有傅里叶变换法(FFT-Fast Fourier Transform Algorithm)、AR(Auto-Regressive)模型法、白噪声法以及谐波叠加法等。研究表明[2]：谐波叠加法理论严密、简单直观、有普适性，具有很好的适应性和高精度，实现起来较为方便，是比较合适的模拟道面激励的方法。因此，本文将采用谐波叠加法来模拟道面不平度。

2谐波叠加法模拟道面不平度

大量的实测数据表明，道面不平度在频域内是具有零均值、各态历经的平稳Gauss随机过程，在时域内是各态历经的平稳随机过程[3]。道面高程q(x)是随空间距离x变化的函数, 示意图[4]见图1。

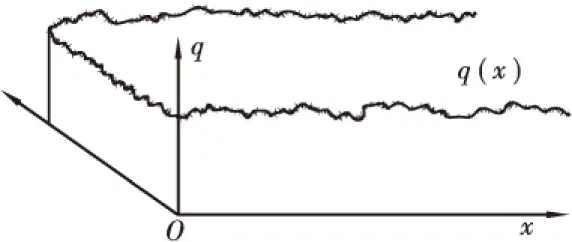
图1　道面不平度示意图Figure 1　Pavement roughness sketch map

研究表明[5]，可以将道面看做是由一组波长、振幅、相位不同的波叠加而成，其叠加原理如图2所示。谐波叠加法源自于道路功率谱估计的周期延拓假设，其基础是三角级数求和，也就是三角级数模拟，是以离散谱逐渐逼近目标随机过程的随机模型，该模型数学基础严密，建立的道路模型具有普适性，能科学、客观、合理的对道面输入模型进行重构，而且具有良好的适应性和高精度。由于机场道面高程激励可以认为是均值为零、各态历经的Gauss平稳随机过程，因此从理论上讲，任意一条道面轨迹都可以认为是一系列相位随机的正弦波的叠加。

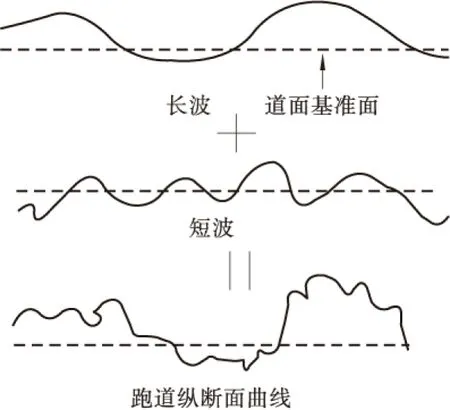
图2　道面纵断面波形组合Figure 2　Pavement profile wave combination

作为本文研究对象的道面不平度，一般都在频域上采用功率谱密度(PSD-PowerSpectralDensity)的形式对其统计学特性进行描述。由国际标准化组织文件ISO/TC108/SC2N67中的《路面不平度表示方法草案》和国内长春汽车研究所编制的《车辆振动输入-路面平度表示》(GB7031-87)两个文件可知: 道面不平度功率谱密度Gq(n)及不平度方差可用式(1)拟合表达：

Gq(n)=Gq(n0)(n/n0)-w

(1)

式中:n表示空间频率有效频率宽度范围内的某一空间频率，表示每米长度包括几个波长，n(n1,n2)，n1和n2分别为有效频率的上限和下限；n0=0.1 m-1，为空间参考频率；Gq(n0)为不平度系数(功率谱密度)，与路面等级相对应，具体数值见表1；w为频率指数，决定着路面功率谱密度的频率结构，一般情况下取w=2。

由于将道面看做一组波长、振幅、相位不同的正弦波的叠加，则可以假设该组波的空间频率(波长的倒数)范围为(n1,n2)，将区间(n1,n2)划分为N个小区间，第i个小区间的中心频率为nmid-i,区间宽度为Δn, 则所对应的道面位移功率谱密度为Gq(ni)则：

(2)

nmid-i=n1+(i-1/2)Δn

(3)

(4)

(5)

(6)

式中：x为道面长度；q(x)为道面高程激励；N为将频率范围(n1,n2)均分所得小区间数量；αi为均匀分布于[0,2π]的随机数。

表1 路面不平度分类标准节选[7-9]Table1 Excerptofclassificationstandardofpavementroughness路面等级Gq(n0)/(10-6m3)(n0=0.1m-1)σ/(10-3m)(0.011m-1

表1是公路等级区分标准，国际上一般用国际平整度指数IRI来划分机场道面的等级，划分标准见表2。

国际平整度指数IRI和功率谱密度Gq(n0)有如下相关关系[10]：

(7)

表2 国际平整度指数分级标准Table2 GradingstandardoftheInternationalRoughnessIndex评价等级IRI平均值(m·km-1)好≤2.0中>2.0,≤4.0差>4.0

其中：a0=103m-1.5，为常数。

由式(7)可建立功率谱密度PSD(即Gq(n0))和国际平整度指数IRI的换算关系，继而可得不同等级的道面所对应的Gq(n0)见表3。

表3 不同道面等级对应的PSD值Table3 ThecorrespondingPSDvaluesofdifferentpave-mentgradeIRIGq(n0)/(10-6m3)IRIGq(n0)/(10-6m3)1.01.644.026.32.06.575.041.13.014.8

当道面统计的空间频率分布在0.011m-1到2.830m-1之间时，能够包含飞机悬挂系统的固有频率，因此，n1=0.011 m-1；n2=2.830 m-1，参考空间频率[11]n0=0.1 m-1；频率指数w=2.00；为了使仿真足够精确，取所划分区间数目N=500；取仿真道面长度为150 m。

根据式(1)～式(5)，在MATLAB环境中编写道面命令流如下：

x=0∶0.1∶150; !采样间距及仿真道面长度

n0=0.1;

Gq_n0=1.64e-6; !功率谱密度取值

delt_n=0.0056;

thta=2*pi*(rand(1,10000));!随机数θ

q=0;

for j=1∶1500

n=delt_n*(j-0.5)+0.011; !小区间中心频

率nmid-i

Gq_n=Gq_n0*n0^2/n^2;

Ai=sqrt(2*Gq_n*delt_n);!功率谱标准差(振幅)

q=q+Ai*sin(2*pi*n*x+thta(j) );

end

将以上命令流输入到MATLAB中，通过变换Gq(n0)取值而模拟不同的道面，参考表2和表3，分别对好(IRI<2)、中(24)3个等级的道面进行模拟，结果如图3～图5所示：

对比图3～图5可知: 随着道面等级(按功率谱密度定义)的降低，道面高程值和其变化量越来越大。IRI=1.0的道面激励取值范围：-0.006～0.006 m；IRI=3.0的道面激励取值范围：-0.01～0.01 m；IRI=5.0的道面激励取值范围：-0.016～0.016 m；这与实际相符合。运行程序后，可在2S之内可以得到计算结果，鉴于对道面所取的仿真步长较小，说明所编程序运行效率较高。

图3　IRI<2(取IRI=1.0)的道面不平度曲线Figure 3　Pavement roughness curve when IRI<2(take IRI=1.0)

图4　2

图5　IRI>4(取IRI=5.0)的道面不平度曲线Figure 5　Pavement roughness curve when IRI>4(take IRI=5.0)

将得到的道面不平度曲线进行频率分析，得到其频谱分布如图6～图8，并与标准路面谱进行对

图6　IRI=1.0时的目标功率谱与模拟功率谱Figure 6　The target power spectrum and the simulated power spectrum when IRI=1.0

图7　IRI=3.0时的目标功率谱与模拟功率谱Figure 7　The target power spectrum and the simulated power spectrum when IRI=3.0

图8　IRI=5.0时的目标功率谱与模拟功率谱Figure 8　The target power spectrum and the simulated power spectrum when IRI=5.0

比。其中标准路谱是按国家标准给出的路面功率谱密度Gq(n)的值得到的[12]。

由图6～图8可以看出: 模拟功率谱与目标功率谱基本重叠，走向趋势也较为一致，拟合精度较高。说明用谐波叠加法模拟道面的方法有着较高准确度和精度。

3结论

本文对机场道面不平度的计算机模拟方法-谐波叠加法进行了研究。对该方法进行了理论推导，并以推导过程中相关数学表达式为依据用MATLAB语言进行了编程。利用该方法对3个不同等级的道面不平度进行了仿真模拟，并通过谱估计对比了所模拟道面的功率谱与标准道面功率谱，结果证明，通过谐波叠加法模拟的道面不平度精度较高，与标准道面谱契合度较高，能够满足对道面不平度重构的需要，并且该种方法思路清晰、理论严密、结果准确、便于实现，为飞机相关的振动特性及疲劳耐久性等研究奠定了基础。

[参考文献]

[1]徐占，过学迅，汪斌. 标准路面谱重构及软件实现[J]. 汽车科技,2009(3): 23-26.

[2]彭佳，何杰，李旭宏，等.路面不平度随机激励时域模型的仿真比较与评价[J]. 解放军理工大学学报:自然科学版,2009,10(1):77-82.

[3]Lu Sun. Simulation of Pavement Roughness and IRI Based on Power Spectral Density[J]. Mathematics and Computers in Simulation，2003，61(4)：77-88.

[4]张永林. 车辆道路数值模拟与仿真研究[D]. 武汉：华中科技大学,2010.

[5]邓松武. 跑道平整度及道面破损对飞机运行的影响研究[D]. 天津：中国民用航空学院,2006.

[6]赵济海，王哲人.路面不平度的测量分析与应用[M]. 北京：北京理工大学出版社，2000.

[7]GB/T 7031-1986，车辆振动输入与路面平度表示方法 [S]．

[8]GB/T 7031-2005，机械振动道路路面谱测量数据报告[S].

[9]郑海腾，李尚平，李冰，等.基于谐波叠加法的标准路面重构[J]. 机械研究与应用，2014,27(134):82-86.

[10]薛华鑫. 飞机滑行状态下振动频率响应分析[D] . 天津：中国民航大学，2014.

[11]潘双夏，陈助碧，冯培恩. M-File S-函数在时域路面不平度建模中的应用[J]. 中国机械工程学报，2006,4(4):379-384.

[12]常志权，罗虹，褚志刚，等.谐波叠加路面输入模型建立及数字模拟[J]. 重庆大学学报:自然科学版，2004,27(12):5-8.

Research of Airport Pavement Roughness Simulation Technology Based on MATLAB

CHENG Guoyong， GUO Wenhou， LEI Yawei

(1.Airport College,Civil Aviation University of China,Tianjin 300300,China)

[Abstract]In order to study the vibration response of aircraft caused by pavement excitation, pavement profile curves were needed,which was pavement roughness.This paper studied the pavement roughness simulation method based on harmonic superposition method；described the principles and characteristics of the method ; programmed the procedure of random pavement generated by this method; simulated three different grades of pavement roughness and got roughness sequences of corresponding pavement grade.Compared the simulation pavement spectrum and the standard pavement spectrum by the power spectrum estimation method, the two results were consistent and this showed that the harmonic superposition method was Very appropriate for pavement roughness Simulation.

[Key words]pavement roughness; harmonic superposition method; Power spectral density; Software development

[收稿日期]2015-02-10

[基金项目]国家自然科学基金资助项目(51178456)；中央高校基金B类项目(3122014B003)

[作者简介]程国勇(1971-)， 男，河北衡水人，教授，主要从事机场场道工程及岩土工程研究。

[中图分类号]U 416.2

[文献标识码]A

[文章编号]1674-0610(2016)03-0005-03