子空间投影后波束形成的导航接收机抗干扰性能分析*

关刚强，聂俊伟，黄仰博，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙　410073)



子空间投影后波束形成的导航接收机抗干扰性能分析*

关刚强，聂俊伟，黄仰博，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙410073)

摘要：利用导航信号淹没于干扰信号和热噪声的特点，将天线阵列接收的空时信号矢量向干扰子空间的正交子空间投影以实现干扰抑制。当接收机对投影后的单阵元数据捕获成功后，利用捕获估计的本地扩频码相位作为参考信号，依据最小均方误差准则进行波束形成。仿真结果表明该抗干扰算法在零陷强干扰的同时使主波束指向导航信号来波方向，有效提高了阵列输出信干噪比，并降低了空时自适应处理对导航信号伪码相关峰形状和载波跟踪性能的影响。

关键词：抗干扰；子空间投影；波束形成；导航接收机

空时自适应处理技术在不增加阵元的前提下，通过在每个阵元后连接延时单元，可以较大程度增加自适应天线阵列的自由度，能够同时实现抗窄带和宽带干扰的目的，在导航领域有着极广阔的应用前景[1]。

国内外已有相关文献对阵列天线导航接收机抗干扰技术进行了广泛的研究，如文献[2]分析了空时、空频自适应处理的抗干扰性能及其影响因素。文献[3-7]对利用子空间投影技术的抗干扰性能进行了研究，其分析结果表明该技术可以有效地实现干扰抑制，但不能增强导航信号。波束形成技术能够显著提高天线阵列对信号来波方向的增益，但在干扰方向上形成零陷一般需要通过附加约束条件实现，针对波束形成技术的研究参见文献[8-10]。

在建立空时自适应处理信号模型的基础上，本文提出了一种结合子空间投影和波束形成技术的空时自适应处理抗干扰算法，通过数学仿真验证了该算法的抗干扰性能，并分析了抗干扰处理对导航接收机相关峰曲线和载波跟踪性能的影响。

1空时自适应处理信号模型

典型的阵列天线空时自适应处理框图如图1所示，其中阵列天线由N个阵元组成，每个阵元后接有L阶时域有限长单位冲激响应(FiniteImpulseResponse,FIR)滤波器，每个数据节拍时延为T0。对于同一天线阵元，FIR滤波器可从时频域上对信号进行分析从而实现干扰抑制；而对于同一个数据快拍，不同阵元组成空域滤波器，可在干扰方向形成零陷；因此空时自适应处理结构扩展了信号处理的自由度，更多地利用了输入信号的参数特征，理论上能达到更好的干扰抑制效果[1,11]。这里假设阵元数等于通道数，即各阵元接收到的信号经过各自的射频前端预处理后送到空时自适应处理器。

图1　阵列天线空时自适应处理框图Fig.1　Block diagram of STAP using antenna arrays

考虑M个远场信号入射到某空间阵列上，将天线阵列N个阵元接收的L个快拍数据组成列矢量，则有：

(1)

其中，xn(k-mT0)为k时刻第m个快拍的N×1维数据列矢量，则有：

(2)

其中：θi为信号入射到天线阵列的仰角；a(θ)为导航信号入射到阵列的空时导向矢量；b(θi)为第i个干扰信号的空时导向矢量；s(k)，ji(k)分别表示导航信号和干扰信号的时域波形采样；n(k)为空时不相关的加性复高斯白噪声列矢量。将式(2)用矩阵形式表示，则有：

(3)

假设阵列接收数据中导航信号、干扰和噪声是互不相关且均值为零的广义平稳随机过程，则快拍协方差矩阵可以表示为：

(4)

其中：δ2为噪声功率，Rs、RI分别为导航信号和干扰信号的空时协方差矩阵，I为单位矩阵。阵列加权矢量表示为：

w=[w11,w21,…,w1L,…,wN1,wN2,…,wNL]T

(5)

则经过天线阵列空时自适应处理后的输出为：

y(k)=wHx(k)

(6)

阵列信号空时自适应处理技术就是通过在某种最优化准则下寻求最优权矢量来达到抑制干扰信号并保护有用信号的目的。

2子空间投影抗干扰

对阵列接收数据协方差矩阵进行特征分解并将特征值矩阵从大到小排列，则有：

(7)

其中：λi为阵列协方差矩阵的特征值，且满足λ1≥λ2≥…≥λP>λP+1=…=λNL，ui为特征值λi对应的特征矢量[12]。由于导航信号接收功率远小于干扰信号和噪声基底，因此定义大的P个特征值对应的特征向量张成的子空间为干扰子空间UI，对应的NL-P个小的特征值对应的特征向量张成的子空间为信号噪声子空间UN。根据特征值分解理论，干扰子空间和信号子空间互为正交补子空间，且干扰子空间与干扰信号入射到阵列的导向矢量张成的子空间相同[12]，即有：

(8)

span{u1,…,uP}=span{b(θ1),…,b(θM-1)}

(9)

通过将天线阵列接收数据矢量向噪声子空间投影，可以有效抑制干扰分量，子空间投影后的数据矢量将主要包含噪声和淹没其中的导航信号，即

xs(k)=P⊥x(k)

(10)

3基于最小均方误差准则的波束形成技术

为提高阵列天线输出数据的信噪比，如图2所示，首先对子空间投影干扰抑制后的单阵元数据进行捕获，估计出导航信号伪码相位和载波多普勒，然后利用同步后的本地伪码作为参考信号依据最小均方误差准则进行自适应波束形成，使阵列波束指向导航信号来波方向。在接收机码环对导航信号跟踪的同时，波束形成算法完成对空时自适应滤波器权值的更新。从而在导航卫星运动过程中阵列天线的波束始终对准导航信号来向，高信噪比的阵列输出信号又将有助于提升导航接收机跟踪环路的稳定性和跟踪精度。

图2　子空间投影及波束形成处理框图Fig.2　Block diagram of subspaceprojection and beamforming

经过子空间投影及波束形成后的输出数据与已同步的本地伪码作为的参考信号之间的误差量可以表示为：

e(k)=r(k)-y(k)=d(k-τ)-wHP⊥x(k)

(11)

其中，d(t)为本地伪码，τ为导航信号从卫星至接收机天线相位中心的传播时延，由对参考天线接收数据精捕获得到。

为了表示方便，将式(11)中的时间变量k省略，这样均方误差量可以表述为：

(12)

利用式(13)求均方误差量MSE对权值向量w的梯度，可得：

(13)

其中，Rxd=E[xHd]为阵列接收数据与参考信号的互相关矢量。

波束形成所依据的最小均方误差准则即寻找最优化权值矢量使均方误差最小，采用最小梯度迭代算法，可得阵列权值矢量的递推更新公式[13]为：

w(k+1)=w(k)+μw(MSE)

(14)

其中，μ为最小梯度算法的步长因子。

将式(14)带入式(15)可得：

w(k+1)=(I+2μP⊥RxP⊥)w(k)-2μP⊥Rxd

(15)

4抗干扰处理对导航信号的影响分析

阵列天线空时自适应处理过程实现干扰抑制的同时可能引起信号伪码相关峰函数变形、偏移和载波相位偏差等现象，抗干扰输出与本地伪码的互相关函数可以表示为：

(16)

其中，T为积分时间。

假设经过空时处理后阵列输出的干扰信号被抑制，且考虑到信号、干扰和噪声互不相关，因此有：

(17)

其中，h(t,θ)为阵列空时自适应处理器的时域冲击响应函数，Rdd为导航信号的自相关函数。

阵列输出与本地伪码的互相关函数用导航信号的功率谱密度在频域表示为：

(18)

其中，P(f)为导航信号的功率谱密度函数，H(f,θ)为空时处理单位脉冲响应函数的傅里叶变换，且有：

(19)

当自适应权值矢量与导航信号在干扰子空间的正交空间上的投影一致时，阵列空时处理的冲击响应函数为单位冲击响应，此时阵列输出与本地伪码的相关峰函数没有畸变，否则阵列的空时处理将引入误差因素，引起导航接收机定位精度的下降。

5仿真分析

考察采用5个阵元以间距为0.5λ组成的均匀线阵在接收GPSL2频点导航信号的导航接收机性能，其中λ为L2频点中心频率1268.52MHz的波长。每个阵元后自适应时域滤波器的阶数为7。设定仿真场景为信号入射到阵列的仰角为34°，载噪比为50dB-Hz，1个单频连续波干扰及2个窄带干扰分别以15°，62°和4°仰角入射，干噪比都为50dB，3个干扰频率相对于B3频点中心频率的偏差分别为-3MHz，0MHz和6MHz，窄带干扰的干扰带宽同为2MHz。接收机AD采样率为65MHz，前端滤波器带宽为22MHz，数字下变频中频频率为48.16MHz，抽取系数为3，伪码跟踪环路等效带宽为1Hz，载波跟踪采用二阶环路，其等效环路带宽设定为25Hz，环路更新时间为1ms。

如图3所示，对比子空间投影算法前后参考阵元接收数据的功率谱密度，可以看出经过子空间投影，干扰信号得到有效的抑制。图4为采用子空间投影与波束形成的空时自适应处理波束方向图，从中可以看出在单频干扰的角度和频率位置处形成了点状深度零陷，而在两个窄带干扰处形成了带状零陷，零陷深度为45dB左右，干扰的带宽越宽，形成的带状零陷也越宽。并且经过波束形成，阵列方向图的最大增益位于信号的来波方向34°附近，最大增益幅度为5dB左右。图5为波束形成过程均方误差量随时间的迭代曲线，从图5中可以看出均方误差随时间基本呈指数下降，这是符合最小梯度算法特点的。如图6所示，把经过天线阵列空时自适应处理的输出数据和理想信号无干扰数据分别与本地伪码的相关峰函数对比，可以看出，伪码相关峰函数经过空时自适应处理后有较轻微的形变，且相关峰函数的最大副峰值有明显的增大。图7和图8分别为采用子空间投影抗干扰和波束形成后的接收机码环及载波环与接收机接收无干扰理想信号的码环及载波环的跟踪误差对比。不难发现，波束形成算法相对提高了接收机码环的跟踪性能。而载波环路的跟踪误差则没有明显的区别，这是因为阵元后的时域滤波器是线性相位响应的FIR滤波器，而且接收机载波跟踪环路也有滤波效果，但总体而言空时自适应处理对导航信号载波相位的影响较小。

图3　阵元数据在子空间投影前后功率谱密度Fig.3　PSD comparison between before and afterorthogonal subspace projection

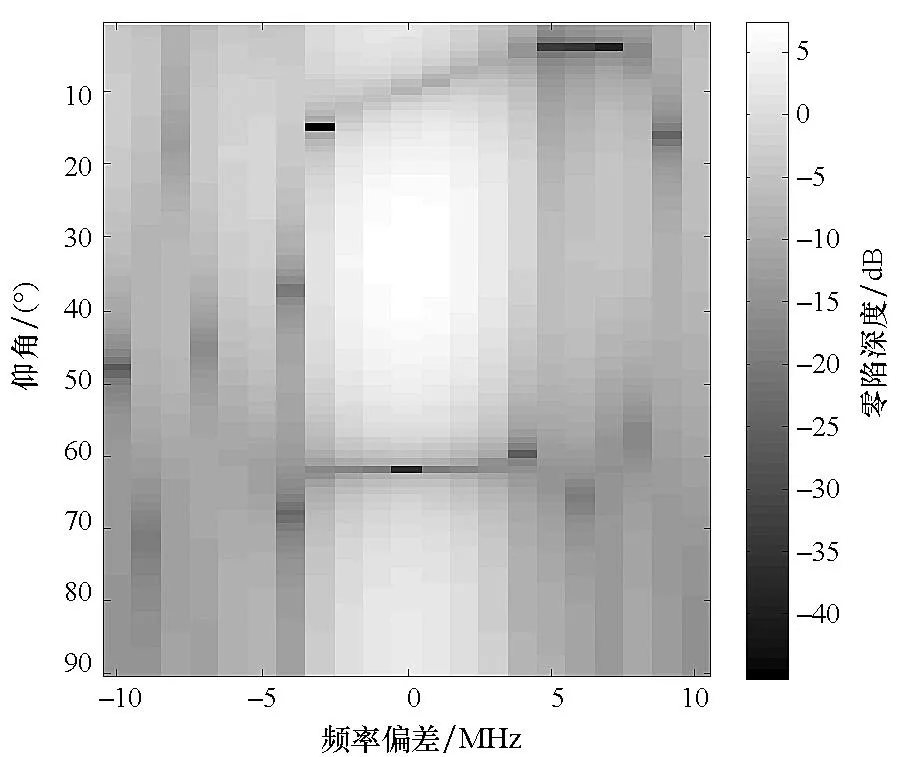
图4　天线阵列波束方向图Fig.4　Antenna array beampattern

图5　波束形成均方误差迭代曲线Fig.5　Beamforming MSE iterative curve

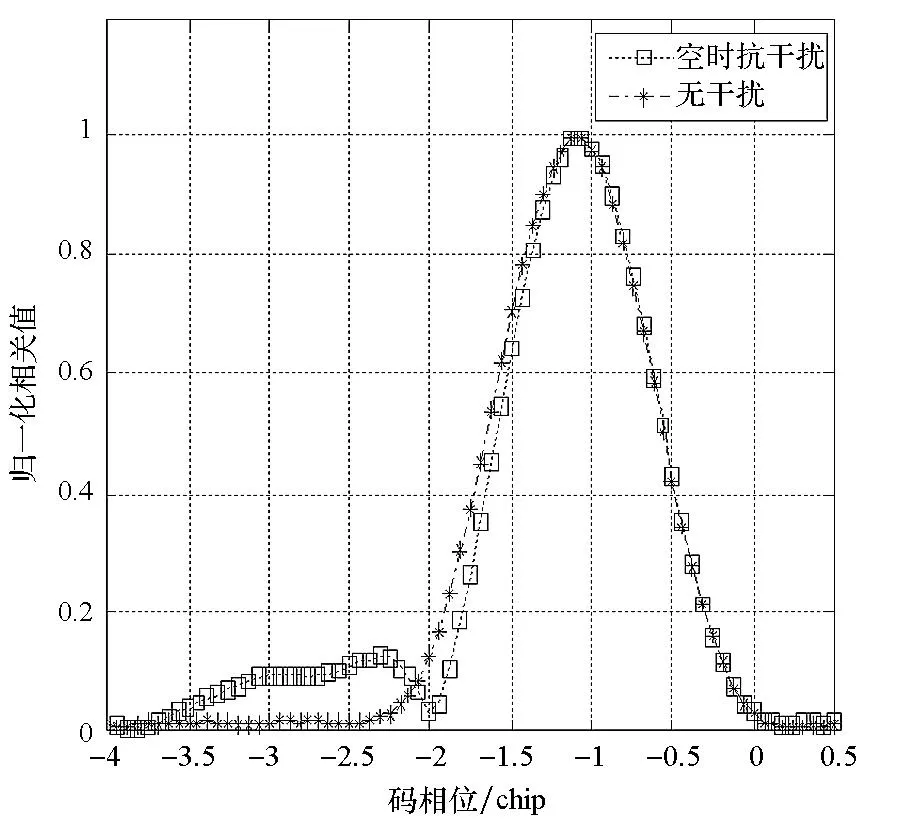
图6　经过空时自适应处理后精捕获的相关峰函数Fig.6　Correlation peak function of fineacquisition after STAP

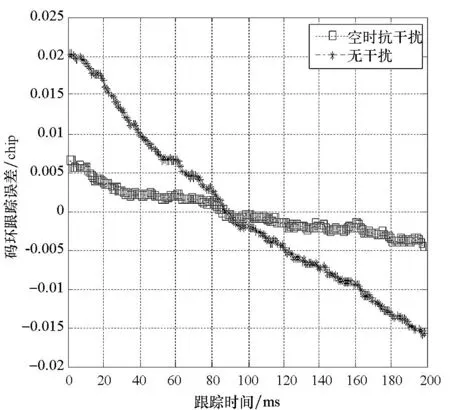
图7　接收机码环跟踪误差对比Fig.7　DLL tracking error comparison of GNSS receiver

图8　接收机载波跟踪误差对比Fig.8　PLL tracking error comparison of GNSS receiver

6结论

算法分析和实验仿真结果表明，采用子空间投影和波束形成算法的空时自适应阵列处理技术可有效抑制干扰信号并提高阵列输出信干噪比。阵列天线空时抗干扰处理会引起导航信号伪码相关峰函数形变，但对普通导航用户而言，由此引起的接收机跟踪误差是可以忽略的。

参考文献(References)[1]郭文飞. 抗干扰GPS接收系统关键技术研究与实现[D]. 武汉: 武汉大学, 2011.

GUOWenfei.Researchandimplementationofkeytechnologiesinanti-jammingGPSreceiver[D].Wuhan:WuhanUniversity, 2011.(inChinese)

[2]MooreTD.Analyticstudyofspace-timeandspace-frequencyadaptiveprocessingforradiofrequencyinterference[D].USA:theOhioStateUniversity, 2002.

[3]ZhangYM,AminMG.ArrayprocessingfornonstationaryinterferencesuppressioninDS/SScommunicationsusingsubspaceprojectiontechniques[J].IEEETransactionsonSignalProcessing, 2001, 49(12): 3005-3014.

[4]UtschickW.Trackingofsignalsubspaceprojectors[J].IEEETransactionsonSignalProcessing, 2002, 50(4): 769-778.

[5]AminMG,ZhaoL,LindseyAR.SubspacearrayprocessingforthesuppressionofFMjamminginGPSreceivers[J].IEEETransactionsonAerospaceandElectronicSystems, 2004, 40(1): 80-92.

[6]DoukopoulosXG,MoustakidesGV.Fastandstablesubspacetracking[J].IEEETransactionsonSignalProcessing, 2008, 56(4): 1452-1465.

[7]DaneshmandS,BroumandanA,NielsenJ,etal.Interferenceandmultipathmitigationutilizingatwo-stagebeamformerforglobalnavigationsatellitesystemsapplication[J].IETRadarSonarandNavigation, 2013, 7(1): 55-66.

[8]RahmaniM,BastaniMH.Robustandrapidconvergingadaptivebeamformingviaasubspacemethodforthesignal-plus-interferencescovariancematrixestimation[J].IETSignalProcessing, 2013, 8(5): 507-520.

[9]李洪涛.自适应数字波束形成关键技术研究[D]. 南京:南京理工大学, 2012.

LIHongtao.Researchonkeytechnologiesofadaptivedigitalbeamforming[D].Nanjing:NanjingUniversityofScience&Technology, 2012.(inChinese)

[10]Dosaranian-MoghadamM,BakhshiHR,DadashzadehGR,etal.AdaptivebeamformingmethodbasedonconstrainedLMSalgorithmfortrackingmobileuser[C]//ProceedingsofGlobalMobileCongress, 2009: 1-6.

[11]DeLorenzoDS.NavigationaccuracyandinterferencerejectionforGPSadaptiveantennaarrays[D].USA:StanfordUniversity, 2007.

[12]王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 26-30.WANGYongliang,CHENHui,PENGYingning,etal.Spatialspectrumestimationtheoryandalgorithm[M].Beijing:TsinghuaUniversityPress, 2004: 26-30. (inChinese)[13]WidrowB.Adaptivefilters[M].USA:Holt,RinehartandWinston, 1971: 563-586.

Performance analysis of anti-jamming algorithm in GNSS receiver utilizing subspace projection and beamforming

GUAN Gangqiang, NIE Junwei, HUANG Yangbo, WANG Feixue

(CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)

Abstract：Consideringthattheglobalnavigationsatellitesystemsignalisburiedinthestronginterferenceandthermalnoise,anovelanti-jammingschemewhichutilizessubspaceprojectionandbeamformingmethodwasproposed.Thedatavectorreceivedbyantennaarraywasprojectedontothenoisesubspacewhichisorthogonaltointerferencesubspacetoachieveinterferencesuppression.Whenthelocalcodewassynchronizedwiththereferenceantennajammer-freedata,beamformingwasperformedaccordingtotheminimummeansquareerrorcriterion.Simulationresultsshowthattheproposedmethodcansteerthemainbeamtothedirectionofglobalnavigationsatellitesystemsignalwavewitheffectiveinterferencesuppression,andtheoutputsignal-to-noiseratiocanbesignificantlyincreasedwhilethecorrelationpeakcurveandthecarriertrackingperformancearenotcorrupted.

Keywords：anti-jamming;subspaceprojection;beamforming;globalnavigationsatellitesystemreceiver

doi:10.11887/j.cn.201603009

收稿日期：2015-03-06

基金项目：教育部新世纪人才支持计划资助项目(NCET-08-0144)

作者简介：关刚强(1986—)，男，河南鲁山人，博士研究生，E-mail：closetoqiang@163.com； 王飞雪(通信作者)，男，教授，博士，博士生导师，E-mail：feixuewang_nnc@163.com

中图分类号：TN95

文献标志码：A

文章编号：1001-2486(2016)03-050-05

http://journal.nudt.edu.cn