多方位测量的相位双差GNSS欺骗干扰检测算法*

耿正霖，聂俊伟，李柏渝，李峥嵘，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙　410073)



多方位测量的相位双差GNSS欺骗干扰检测算法*

耿正霖，聂俊伟，李柏渝，李峥嵘，王飞雪

(国防科技大学 电子科学与工程学院， 湖南 长沙410073)

摘要：对于二元天线阵，相位双差检测算法的载波相位双差角度模糊、虚警概率较高，这限制了算法的应用。针对这一问题，提出天线阵方位变化的欺骗干扰检测算法。通过二元天线阵在不同方位估计信号的载波相位双差，进行多次判决，有效消除角度模糊，降低检测的虚警概率，实现二元天线的载波相位双差检测。建立仿真模型，并通过仿真计算分析验证了该方法的有效性。

关键词：载波相位双差；GNSS欺骗干扰检测；方位变化；天线阵

全球导航卫星系统(Global Navigation Satellite System, GNSS)欺骗干扰因其隐蔽性强、危害性大而备受关注，而抗GNSS欺骗干扰也已成为GNSS抗干扰研究的一大重点。早期文献中提出的抗欺骗干扰算法包括信号幅度检测[1]、信号到达时间检测[1]、与惯导设备一致性校验[1]、信号极化方向检测[1]、信号到达角检测[1]、加密认证[1]、接收机完好性监测[2]等，文献[3]对绝对功率检测、功率变化率监测、相对功率检测、多普勒检测、L1/L2互相关检测、星历认证等多种抗欺骗干扰方法进行了比较和分析，给出了各种算法的功能及限制。此后，有学者提出通过监测信号的自动增益控制(Automatic Gain Control, AGC)增益水平[4]以及监测信号载噪比变化率[5]判决欺骗干扰的方法。文献[6]则对基于信号功率、噪声功率以及载噪比的抗欺骗干扰算法进行了较为深入的分析，得到了各种方法的有效性。在基于信号载波相位检测的算法方面，文献[7]提出可利用信号相位进行欺骗干扰检测和抑制，但未对算法进行具体描述。文献[8]提出了采用间距约1.46 m的同源天线对接收信号相位进行测量，同时根据卫星的轨道和天线的位置，估计相位差的真实值，将测量值和真实值进行比较以判决欺骗干扰的算法，但该算法所需时间较长，而且需要知道准确的天线位置以及卫星轨道。

文献[9]提出了相位双差检测算法，分析了利用多元天线阵进行相位双差检测的性能，文献[10]采用相位双差检测算法进行欺骗干扰的判决，提出实现双差检测的最小天线数目，但并未论证最优的天线阵型。本文通过天线的方位变化，在采用双天线条件下，不增加天线数量，有效提升欺骗干扰的检测性能，分析结果对多元天线阵列的构型具有一定的参考价值。

1信号接收模型

假定接收机两天线处于水平面，以两天线间连线所在方向为方位角零度方向，信号入射关系如图1所示。

图1　天线阵列和信号分布示意图Fig.1　Geometry distribution of antenna-array and signal

图1中A，B表示两个接收天线；b为基线矢量，单位为载波周期；S为入射信号单位方向矢量，由接收机指向信号来波方向；θ和φ分别表示入射信号的方位角和俯仰角。以天线A的位置为坐标原点，AB所在直线为X轴，水平面为XOY面建立平面直角坐标系。则S可用θ和φ表示为：

S=[cos(θ)cos(φ),cos(θ)sin(φ),sin(θ)]

(1)

基线矢量b为：

(2)

则

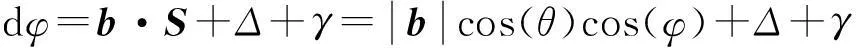
(3)

其中：dφ表示信号在两天线上的载波相位差；Δ表示两个天线的时延差，这对所有信号固定不变；γ表示对信号的相位测量误差之和；对于一般的GPS接收机，载波相位的测量精度为0.01周期[11]，则假设γ～N(0,2σ2)，σ=0.01。对于不同信号，用上标a，s分别表示真实信号和欺骗信号，下标i，m区分卫星号。则有：

(4)

(5)

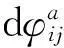
(6)

=γmn

(7)

其中：i,j∈Sa；m,n∈Ss；Sa和Ss表示真实信号和欺骗信号的集合；γij=γi-γj，γmn=γm-γn，γij～N(0,4σ2)，γmn～N(0,4σ2)。

ψ表示信号到达接收天线平面的入射角，有cos(ψ)=cos(θ)cos(φ)，所以式(7)可写为：

(8)

(9)

2双天线检测性能

假设两个天线上的相位双差观测量为Δφ。构造假设：H0——至少有一个为真实信号；H1——两个信号均为欺骗信号。

(10)

相位双差Δφ在H0条件下的概率密度函数如式(11)所示。

(11)

则

p(Δφ;H0)=∫p(Δφ|φ0;H0)p(φ0)dφ0

(12)

通过化简得到H0和H1条件下Δφ的概率密度函数。

(13)

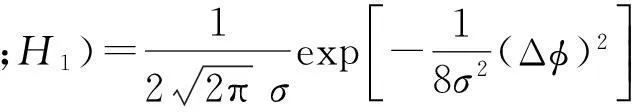
(14)

图2显示了不同基线长度的二元阵在H0条件下相位双差的概率密度。

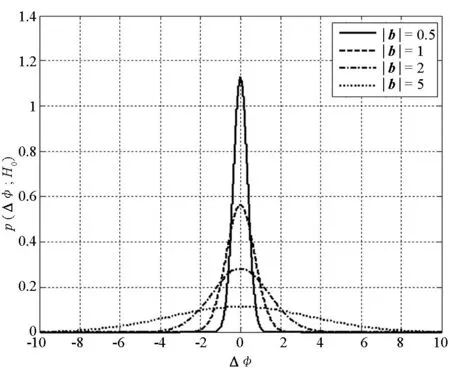
图2　H0条件下不同基线长度对应的相位双差概率密度曲线Fig.2　PDF curves of carrier phase double difference withdifferent base lines under H0

由图2可以看出，随着天线阵元间距的增加，概率密度曲线逐渐平缓。考虑到当基线长度大于半波长时会出现相位模糊，采用半波长的天线阵进行仿真分析。图3为基线长度为半波长的天线阵在H0及H1条件下的概率密度曲线。

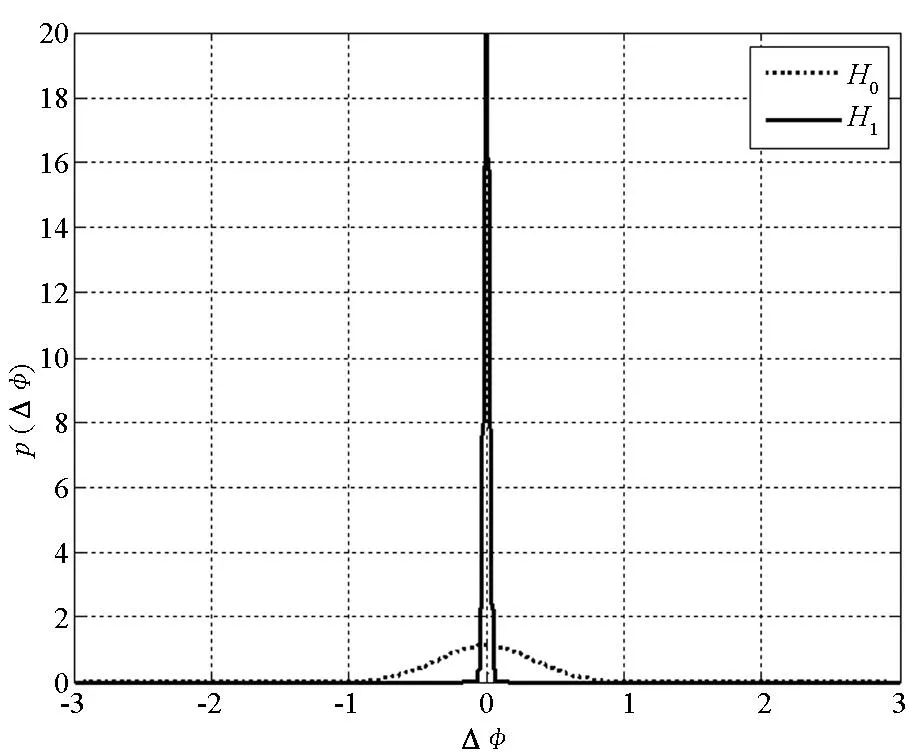
图3　H0,H1条件下的相位双差概率密度曲线Fig.3　PDF curves of carrier phase doubledifference under H0and H1

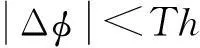
虚警概率为：

(15)

检测概率为：

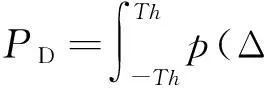
(16)

半波长条件下的检测概率和虚警概率随判决门限的变化曲线如图4所示。同时，可以得到在不同基线长度条件下的受试者工作特征(Receiver Operating Characteristic， ROC)曲线，如图5所示。

图4　检测概率、虚警概率随判决门限的变化曲线Fig.4　Variation curves of detection probability andfalse alarm probability with different thresholds

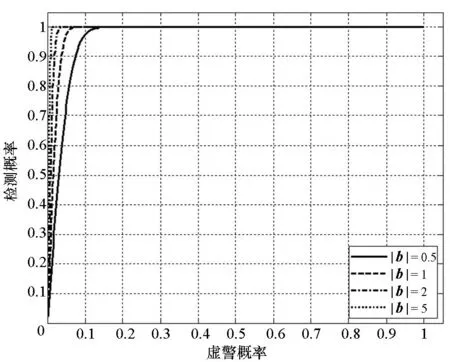
图5　不同基线长度下的ROC曲线Fig.5　ROC curves with different base lines

由图5可以看出，随着基线长度的增加，虚警概率逐渐下降，检测性能相应提升。对于基线长度为半波长的二元天线阵，要实现100%的检测，虚警概率将达到10%以上。由式(8)、式(9)可知，当进行双差计算的两个信号均为欺骗干扰时，相位双差为0，且与信号的入射角度无关。而真实信号的双差随入射角度的变化而变化，因此，可以通过天线阵的方位变化，对不同角度时的相位双差结果进行多次判决，从而有效降低算法的虚警概率。

3算法分析

A点固定，旋转天线阵。以α表示水平方向上的旋转角度，β表示垂直方向上的旋转角度。则经过水平方向α，垂直方向β的旋转后，基线矢量为：

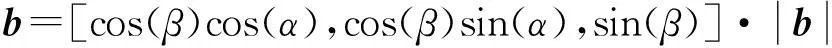
(17)

则

(18)

至少有一个为真实信号时的相位双差为：

(19)

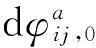
(20)

考虑到旋转天线阵的目的是为了使原本相位双差为0或者接近于0的真实信号在入射角度改变后相位双差绝对值增大，避免被误判为欺骗干扰，故重点考虑原始双差为0的情况。假设原始相位双差为0，则式(20)可写为：

(21)

可以看出，式(21)的最大值与信号原入射角相关，即要使得天线旋转后的相位双差达到最大，不同的信号入射角度得到的最优的旋转角度不同。下面分别从水平方向和垂直方向展开分析。

3.1水平旋转

假设天线阵水平旋转角度为α，垂直方向旋转角度β=0，由式(19)得到，仅在水平方向上旋转后的相位双差为：

(22)

在假设原始相位双差为0的条件下，式(22)可写为：

(23)

显然，在入射角度固定的情况下，当sin(α)=±1时，即旋转与原方向垂直时，相位双差绝对值最大。

3.2垂直旋转

假设天线阵垂直旋转角度为β，水平方向旋转角度α=0，则旋转后的相位双差为：

(24)

在假设原始相位双差为0的条件下，式(24)可写为：

(25)

同样，在入射角度固定的情况下，当sin(β)=±1时，即垂直旋转与原方向垂直时，相位双差绝对值最大。

由此可知，相位双差的最大值是和原入射角度相关的，难以通过天线旋转准确得到。但通过只在水平方向或垂直方向转动，可以得到相应条件下的最大值。对于多元天线阵列，采用相互垂直的天线构型，可以在一个方向上相位双差较小的情况下，在其他两个方向得到较大的相位双差。

根据上述分析，提出相应的欺骗干扰检测算法，算法步骤为：

1)利用水平放置的二元天线阵对接收到的信号进行载波相位测量，计算得到不同信号间的载波相位双差；

2)水平旋转天线阵，使其基线方向与原基线方向垂直，测量接收到信号的载波相位，计算得到不同信号间的载波相位双差；

3)垂直旋转天线阵，使其基线方向与原基线方向垂直，测量接收到信号的载波相位，计算得到不同信号间的载波相位双差；

4)对三次测量得到的相位双差进行判决，若在三次测量中，两个信号的相位双差均小于门限，则判为欺骗干扰，若至少一次双差大于门限则判为真实信号。

4检测性能

采用MATLAB进行仿真分析，设置不同的天线阵型及信号入射角度，模拟真实信号和欺骗信号入射的情况，分析不同阵型下的相位双差检测算法性能以及本文方法的检测性能。

以四阵元为例构建模型，如图6所示。A1～A4表示四个天线阵元。固定阵元A1，A2的位置，A1坐标为(0,0,0)，A2坐标为(λ/2,0,0)，λ为载波波长，A3，A4与A1距离均为λ/2，A3在XOY平面内，A4在XOZ平面内，A3A1和A2A1的夹角为α，A4A1和A2A1的夹角为β。仿真中通过遍历α和β，模拟不同的天线阵型，α遍历范围为0°～180°，β遍历范围为0°～90°。

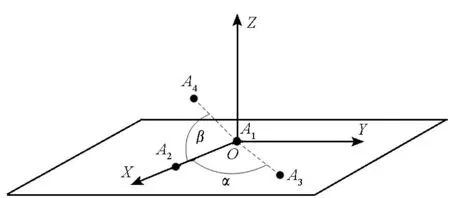
图6　天线阵型示意图Fig.6　Diagram of antenna array

仿真中假设信号入射角度在俯仰角0°～90°，方位角0°～360°范围内均匀分布。以两个入射信号为例，取200 000组不同的信号入射方向，针对不同的阵型统计出现虚警的次数，计算虚警概率，如图7所示。

图7　不同阵型下的虚警概率Fig.7　False alarm probability under different antenna-arrays

由图7可知，当α在0°或180°附近时，出现虚警的概率较高，而当α在90°附近时虚警概率较低。当β固定，α变化时，得到几个典型值下的虚警概率变化情况，如图8所示。当α固定，β变化时，得到几个典型值下的虚警概率变化情况，如图9所示。

图8　不同β取值下PFA随α的变化情况Fig.8　Variations of PFAwith changes of α under different β

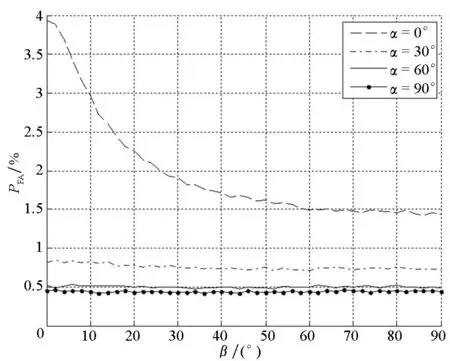
图9　不同α取值下虚警概率随β的变化情况Fig.9　Variations of PFAwith changes of β under different α

由图8可以看出，随着β逐渐增大，不同α取值下的虚警概率整体减小，当β=90°时，达到最小；而当β固定时，虚警概率的最小值均出现在α=90°附近。由图9可以看出，随着α逐渐增大，不同β取值下的虚警概率也整体减小，当α在30°～90°之间时，β对虚警概率的影响较小。结合仿真结果可以看出，当α和β均为90°，即立体布阵时具有较优的性能，可以有效降低虚警概率，与平面阵相比，性能有显著提升。这也说明通过二元天线阵在水平方向和垂直方向旋转90°进行相位双差检测的方法具有较好的性能。

下面对该方法的检测性能进行分析。仿真计算信号到达两个放置于X轴，间距半波长的天线的载波相位双差，以及天线水平旋转90°和垂直旋转90°后的相位双差，分析不同检测门限下单次判决的虚警概率和三次判决的虚警概率并与参考文献采用的三元阵的检测性能进行比较。

1)两个信号入射角度不同。仿真两个信号的入射角不同，即至少有一个信号为真实信号的情况。假设两个入射信号的俯仰角和方位角分别在0°～90°和0°～360°内均匀分布，得到不同条件下虚警概率随判决门限的变化情况，如图10所示。

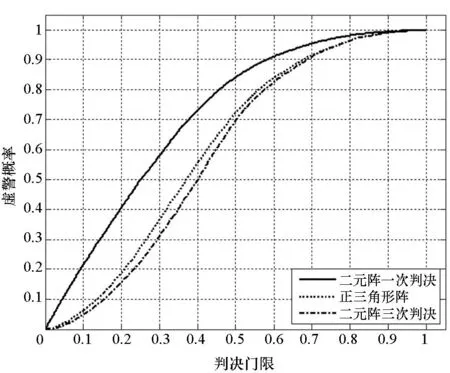
图10　不同判决门限下的虚警概率Fig.10　False alarm probability with different thresholds

2)两个信号入射角度相同。假设两个信号的入射角相同，即模拟两个信号均为欺骗干扰的情况。两个信号的俯仰角和方位角在0°～90°和0°～360°内均匀分布，仿真得到不同条件下检测概率随判决门限的变化情况，如图11所示。

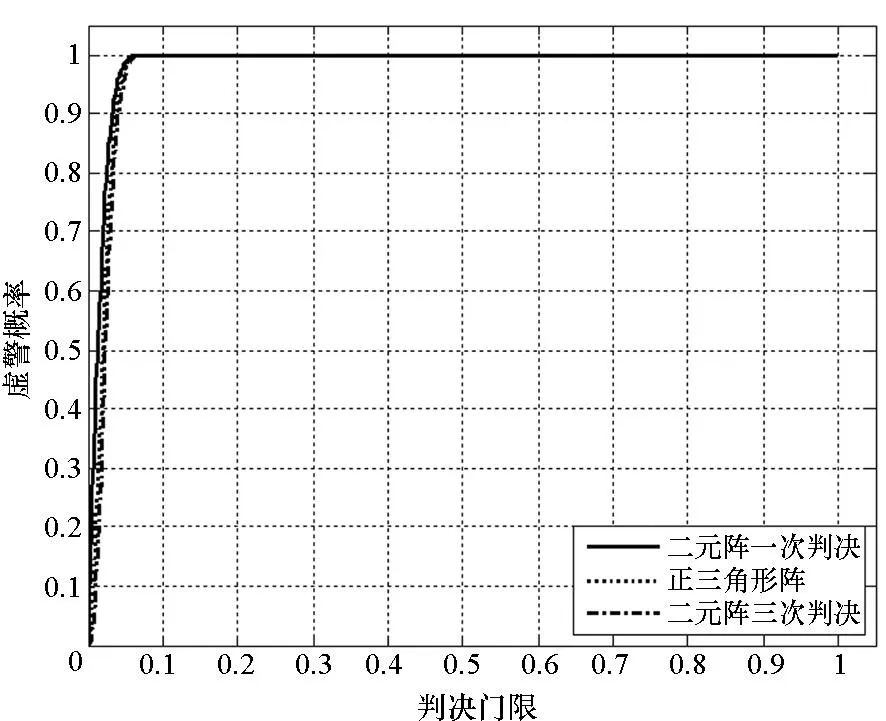
图11　不同判决门限下的检测概率Fig.11　Detection probability with different thresholds

根据上述仿真结果得到不同条件下判决的ROC曲线，如图12所示。

图12　不同判决门限下的ROC曲线Fig.12　ROC curves with different thresholds

由图10～12可以看出，对于二元阵，进行三次判决后的虚警概率明显下降，而对检测概率影响较小。从图12中可以明显看出，采用天线在三个相互垂直的方向上测量得到的相位双差进行判决，其检测性能显著提高，实现100%检测时的虚警概率下降到3%左右。当天线阵列数达到三个时，如文献[10]所述，对于正三角形阵，相位模糊得以消除，虚警概率有效降低，检测性能得到提升，但和本文方法相比，虚警概率略高，性能存在一定差异。

5结论

通过二元天线阵方位变化，在不同方位上测量得到信号双差进行欺骗干扰检测的方法具有如下优点：

1)不需要知道卫星位置以及天线自身精确的位置，检测时间短；

2)不需增加天线阵元数，不需增加设备的硬件复杂度即可实现欺骗干扰的有效检测；

3)可以有效降低虚警概率，同时对检测概率影响较小，进而改善检测性能。

通过分析，还可得到如下结论：在不考虑信号载波相位模糊时，对于二元天线阵的相位双差检测，通过增大天线间距可降低欺骗干扰检测的虚警概率，提升检测性能。仿真结果表明：采用相互垂直的三维立体阵，具有较优的检测效果，即对于真实信号，当一个方向上天线的相位差较小时，在其他两个方向上可以得到较大的相位差，降低出现相位模糊的概率，从而提升检测性能。

参考文献(References)[1]Key E L. Techniques to counter GPS spoofing[R]. The MITRE Corporation Internal Memorandum, Bedord, 1995.

[2]Michalson W R. Ensuring GPS navigation integrity using receiver autonomous integrity monitoring[J]. IEEE Aerospace & Electronic Systems Magazine, 1995, 10(10): 31-34.

[3]Wen H Q, Huang P Y R, Dyer J, et al. Countermeasures for GPS signal spoofing[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2005: 1285-1290 .

[4]Akos D M. Who′s afraid of the spoofer? GPS/GNSS spoofing detection via automatic gain control (AGC)[J]. Navigation, 2012, 59(4): 281-290.

[5]Dehghanian V, Nielsen J, Lachapelle G. GNSS spoofing detection based on receiver C/No estimates[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation, 2012: 2878-2884.

[6]Jahromi A J, Broumandan A, Nielsen J, et al. GPS spoofer countermeasure effectiveness based on signal strength, noise power, and C/N0measurements[J]. International Journal of Satellite Communications & Networking, 2012, 30(4): 181-191.

[7]Mcdowell, Charles E. GPS spoofer and repeater mitigation system using digital spatial nulling: US7250903[P]. 2007-07-31.

[8]Montgomery P Y, Humphreys T E, Ledvina B M. Receiver-autonomous spoofing detection: experimental results of a multi-antenna receiver defense against a portable civil GPS spoofer[C]//Proceedings of the International Technical Meeting of the Institute of Navigation, 2009: 124-130.

[9]黄龙． GNSS 接收机欺骗与抗欺骗关键技术研究[D]． 长沙: 国防科学技术大学， 2013．

HUANG Long． Study on techniques of receiver spoofing and anti-spoofing for global navigation satellite system[D]．Changsha: National University of Defense Technology， 2013． (in Chinese)

[10]张鑫, 庞晶, 苏映雪, 等. 天线阵载波相位双差的欺骗干扰检测技术[J]. 国防科技大学学报, 2014, 36(4): 55-60.

ZHANG Xin, PANG Jing, SU Yingxue,et al.Spoofing detection technique on antenna array carrier phase double difference[J].Journal of National University of Defense Technology, 2014, 36(4): 55-60. (in Chinese)

[11]美斯拉. 全球定位系统——信号、测量与性能[M].2版. 北京: 电子工业出版社, 2008.Misra P K. Global positioning system: signals, measurements, and performance [M]. 2nd ed.Beijing:Publishing House of Electronics Industry, 2008. (in Chinese)[12]Broumandan A, Jafarnia-Jahromi A, Dehghanian V, et al. GNSS spoofing detection in handheld receivers based on signal spatial correlation[C]//Proceedings of IEEE/ION Position Location and Navigation Symposium (PLANS), 2012: 479-487.

Carrier phase double difference GNSS spoofing detection technique based on multi-direction measurements

GENG Zhenglin, NIE Junwei, LI Baiyu, LI Zhengrong, WANG Feixue

(College of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract：Carrier phase double difference GNSS spoofing detection technique is an effective one of those methods based on phase measurement, but the high false alarm probability problem is caused by angle ambiguity for double-element antenna-array. Therefore, a technique based on antenna-array direction change was presented. The carrier phase double differences were estimated in different antenna-array directions, and then the carrier phase double differences were used to discriminate the spoofing signals. In this way, the angle ambiguity can be eliminated, and the false alarm probability was reduced. Simulation results verified the effectiveness of the proposed spoofing detection technique.

Key words：carrier phase double differences; GNSS spoofing detection; direction variation; antenna-array

doi:10.11887/j.cn.201603006

收稿日期：2015-12-30

基金项目：国家自然科学基金资助项目(61403413)

作者简介：耿正霖(1988—)，男，云南昆明人，博士研究生，E-mail：oliver8812@163.com； 王飞雪(通信作者)，男，教授，博士，博士生导师，E-mail：wangfeixue_nnc@163.com

中图分类号：TN95

文献标志码：A

文章编号：1001-2486(2016)03-032-07

http://journal.nudt.edu.cn