一个有关计数问题的探究案例
严洪刚

中图分类号:G632 文献标识码:B 文章编号:1672-1578(2016)05-0154-02
1.背景介绍
新课标的理念更突出了知识过程性目标的重要地位,明确要求学生经历观察、实验、猜想、验证等数学活动过程,学会与他人合作交流,学会从数学角度发现问题、分析问题、解决问题、学会体验成功的喜悦,这是我们课改教学的新动向之一。
浙教版数学实验教材七年级上册学习完第七章图形的初步认识(点与线)及角的内容后,学生对点、线、角等基本的概念已有了一个清楚的认识,在学生平常的学习过程中经常出现一类计数问题,因此我认为有必要安排一个环节对这一类问题作一次探究,使学生对这一类问题有一个比较系统全面的理解。
2.情景描述
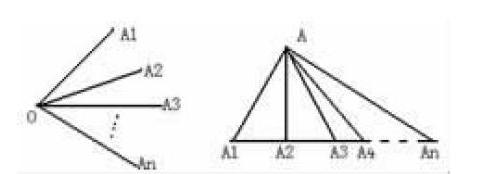
教学中,我开门见山:"同学们,我们一起来看一类有关计数的问题,看看哪个同学会计数。"见学生惊讶的表情,我顺势在黑板上画下两个图形:
接着,我提出问题:"请你们算一下,图(一),图(二)中各有多少条线段?"学生们很快的开始数了,有的同学已经开口说了:"图(一)有3条,图(二)有6条"。也有一些同学出现了遗漏的现象,图(二)答案出现了5条或4条的。
"大家思考都比较积极,我们来想一下,在数线段时,如何数才能不重复、不遗漏呢?"
一学生站起来说:"以A1为左边端点的线段有A1A2,A1A3,A1A4,以A2为左边端点的线段有A2A3,A2A4,以A3为左边端点的线段有A3A4,所以一共有3+2+1=6条。"
"很好,这种方法的确不会重复,也不会遗漏,但是,若直线上有10个点时有多少条线段呢?"
受到刚才这位同学的启发,同学们忙开了,我发现绝大多数同学都是一条一条地去数。看到这种情况,我乘机说:"既然一条一条去数比较烦,那么有没有巧妙的方法呢?比如线段的条数与点的个数之间有没有规律呢?如果我们能找到其中的规律的话,那我们不就省力气吗?各小组分组讨论"
过了一会儿,有些小组迫不急待地开始举手了,我走到她们的桌前,看到了她们写的推理过程: 3个点时有:2+1=3条
4个点时有:3+2+1=6条
5个点时有: 4+3+2+1=10条
6个点时有: 5+4+3+2+1=15条 ……
10个点时有: 9+8+7+6+5+4+3+2+1=45条
看来有些同学已经找到了其中的规律了,但规律还没有表示出来。
又有同学举手了,我叫了其中一个同学回答:因为4个点时是1+2+3=6条,5个点时是1+2+3+4=10条,6个点时是1+2+3+4+5=15条,依此规律,线段的条数是从1开始加到比点数少1的那个数的和。所以10个点就有9+8+7+6+5+4+3+2+1=45条。
"大家同意他的结论吗?"同学们都点了点头。
我乘机提出:"若直线上有n个点呢?你发现有什么规律吗?"
"有规律。"大部分同学都很肯定。我示意他们表示出来。
n个点时是:1+2+3+4+……+n=n(n-1)2条。
我又进一步问道:"还有其他什么方法可得到这个结论吗?"
没人应答,同学们都看着我,有的在环顾四周,看看别人能不能回答。
"我们可以这样考虑,只要确定了线段的两个端点,就确定了一条线段,那么对于n个点,A1、A2、A3、A4、……、An,只需要将其中两个点进行配对,两个点就确定了一条线段,所以我们只要看一下将这n个点进行分组配对,有多少不同的组就有多少线段。"
"对于A1点来说,它可以和其它的A2、A3、A4、……、An这(n-1)个点分别配对分组:A1A2、A1A3、A1A4、……、A1An共(n-1)组,所以就有(n-1)条线段;对于A2来说呢?分别配对分组也有类似的结论得到(n-1)组,所以也有(n-1)条线段,A3、A4、A5、……呢?这样每个点都可以和其余的(n-1)个点分别配对分组也分别得到(n-1)条线段。"
"所以这样n个点就一共可以配对分成n(n-1)组,也就是以两个点为端点线段数一共有n(n-1)条,但是,"我停顿了一下,"这些线段有什么情况出现呢?"
有一个学生回答说:"会重复,因为象A1A2与A2A1是同一条线段。"
"对的,非常正确,这样计数线段数会重复一次,所以真正有的线段数是n(n-1)2条。"
学生恍然大悟。
我接着说:"其实两种方法都不错,运用第二种解释的方法来计数,有些时候是很方便的,我们来举几个例子."我给出了以下几个问题。
(1)平面上有3个点,过其中两点画直线,最多可画几条直线?4个点?5个点?n个点呢?
(2)如图,从O点出发画n条射线,那么图中共有多少个小于平角的角?
(3)如图,图中有多少个三角形?我的问题一抛出,同学们马上七嘴八舌议论开了。一个同学已经惊奇地叫道:结果是一样的,都是n(n-1)2。
我巡视了一圈,发现大部分同学都找到了答案。
"下面有几个练习,看看你能做吗?"我给出了几个练习:
(1)平面上4条直线最多把平面分成几个区域?5条呢?
(2)平面上有10个点,则最多可以画出几条直线?
以其中任一点为端点,通过另外一点的射线有几条?
100个点呢?
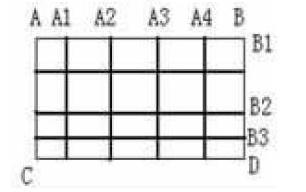
(3)如图,共有_____个长方形。
从练习情况看,还不错。 我乘机说道:"类似的问题在我们平时的学习中还有吗?你能举出其他的例子吗?请你在你的草稿本上写出来。"
学生就忙开了……
一段时间后,我看时间也差不多了,就说:"大家现在停下来,现在我们一起来看看同学们发现了哪些类似的问题?"很多同学马上举起了手。
接下来课堂成了学生的成果展示会。
"平面内有n条直线,若它们两两相交,最多有多少个交点?答案也是n(n-1)2个。"
"全班45个同学互相握一次手,一共要握(45×44)/2次手,如果是n个人就是n(n-1)2次。"
"n个球队进行循环赛,每个队都要和其他队赛一场,一共要赛n(n-1)2场。"
有一个女同学很急切一样,她的问题是:
……
同学们的发言很踊跃,有说n个人一起喝酒,每两个人碰一次杯,一共要碰n(n-1)2次。
我看到这种情况重复出现,话锋一转:还有没有特别一点的?
一个男同学举手了:"我说的是对角线。"
"对角线?"我停了一下,因为我平时提到过对角线,但对于学生毕竟是一个新概念。我说:"你说说"。
"n边形有n个顶点,每个顶点可以向除它本身和左右相邻的两个顶点外的其余(n-3)个顶点画对角线,一共可画n(n-3)条,由于重复一次,所以对角线有n(n-1)2条。"
……
3.教学反思
本案例是一个内容比较简单的复习内容。从教学效果来看,是成功的。
在这一个探究的环节,达成了以下两个教学目标:①在具体情境中,掌握该类计数问题的计数方法。②通过对具体问题的分析,找出该类问题的数学模型。探究环节的重点是掌握该类计数问题的计数方法。学生探究的难点是通过对具体问题的分析,认识到具体问题所在的数学模型。
为了更好地突破难点,我首先在设计上尽量抛开以前的讲授式。而是充分利用学生参与学习和探讨的热情,让学生充分发表意见,通过对问题的争论与讨论,达到对知识的深入理解。因此,探究环节的开始,我首先从一类最简单,最常见的问题出发引入,从学生的知识最近发展区进行提问,一步步发散展开,最后让学生寻找学习中出现的相同数学模型的问题来达到巩固知识的理解。
教学过程中采用让学生讨论的形式,以学生自主探究与合作学习,教师组织、引导的方式进行,并对问题的实际数学模型加以深入,让学生能对知识举一反三。实践证明,这个探究环节的实施是成功的。
但仍然有以下问题值得探讨:(1)本堂课在课堂开始用第二种方法分析线段条数得到计数结果为n(n-1)2,仍然是以教师讲解为主,没有完全放手让学生自己探究获得。
(2)课中一些好的做法值得借鉴,课堂上能放手真正的让学生参与到自主探究的学习中去,这也是今后教学应提倡的做法。
(3)如何充分发挥学生的合作学习,让每个学生都积极动起来,全体参与,共同提高,而不仅仅是少数人讨论,也是今后教学中值得注意的问题。
本堂课的内容看似比较简单,但要求低年级学生对这一 数学模型有一个深入的理解,以达到对知识的融会贯通具有一定的难度,笔者深切地感受到,让学生主动地探究与体会其内在的数学模型是这堂课是否成功的关键。实践证明,学生自己探究并发现的知识记得更牢,并能灵活运用。

